1 Introduction
Traditional benefit-cost analysis and decision analysis typically involves multiple steps such as the following (Raiffa, Reference Raiffa1968; Clemen & Reilly, Reference Clemen Robert and Reilly2014; Howard & Abbas, Reference Howard and Abbas2016):
1. Identify alternative feasible choices, decision rules, or courses of actions. This “choice set,” or set of decision alternatives, may be specified explicitly as a discrete set of alternatives, such as whether or not to fund a public project, or implicitly via constraints on the allowed values of decision variables, such as quantities of limited resources available to be allocated.
2. Identify preferences and value trade-offs for possible outcomes. These may be formally represented via a net benefit function or via a (possibly multiattribute) von Neumann-Morgenstern utility function or social utility function to be maximized (Keeney & Raiffa, Reference Keeney and Raiffa1976).
3. If the outcomes for each choice are uncertain, estimate the probabilities of different outcomes for each choice (e.g., its risk profile); and
4. Optimize choices subject to feasibility constraints (e.g., on available time, budget, or limited resources) to identify and recommend a feasible choice that maximizes expected net benefit, expected utility, or expected social utility of outcomes.
These steps are all well-established parts of prescriptive decision analysis for a single decision-maker and benefit-cost analysis for a social decision-maker (Howard & Abbas, Reference Howard and Abbas2016; Raiffa, Reference Raiffa1968).
In 1959, political economist Charles Lindblom of Yale University pointed out that almost none of these steps can be applied in practice to the decisions and uncertainties faced by real government decision-makers, or by decision-makers in other bureaucracies. Preferences and value trade-offs may be unknown and difficult or impossible to articulate, quantify, and justify. Lindblom (Reference Lindblom1959) wrote, “Typically the administrator chooses – and must choose – directly among policies in which [different] values are combined in different ways. He cannot first clarify his values and then choose among policies,” as multiattribute utility theory prescribes. Even identifying possible outcomes for each feasible choice may be impracticable if the number of possible choices is immense or possible outcomes are unknown. In addition, real-world bureaucratic and organizational decisions are almost never made by a single decision-maker. Rather than seeking to extend or refine normative decision analysis to overcome what he perceived as its fatal practical limitations for large-scale, multiperson organizational decision-making over time, Lindblom instead described a method of successive limited comparisons that he contrasts with the “rational-comprehensive” normative approach favored in benefit-cost analysis, decision analysis, operations research, and optimal control engineering. The rational-comprehensive approach seeks to solve decision optimization problems such as
where
a is a decision variable or policy (e.g., a vector or a time series of decision variables, or a feedback control decision rule mapping observations to actions)
A is the set of feasible alternative decisions (the “choice set”)
R(a) is the reward (expected utility or net benefit) from choosing a. In many traditional economic, policy, and operations research analyses, the reward function to be maximized is assumed to be known. In statistical design of experiments and machine learning, it may have to be discovered. If the reward received depends both on the decision-maker’s choice a and also on other variables not controlled by the decision-maker, collectively referred to as the state and modeled as a random variable s, then R(a) is the expected reward from choosing a given the probability distribution of s. When there are many players, R is often taken to be a weighted sum of individual utility functions (Gilboa et al., Reference Gilboa, Samet and Schmeidler2004).
maxa∈A indicates that an act a in A is to be selected to maximize R(a).
Lindblom wrote that “the attention given to, and successes enjoyed by operations research, statistical decision theory, and systems analysis” have strengthened a “tendency to describe policy formulation even for complex problems as though it followed [this] approach,” emphasizing “clarity of objective, explicitness of evaluation, a high degree of comprehensiveness of overview, and, wherever possible, quantification of values for mathematical analysis. But these advanced procedures remain largely the appropriate techniques of relatively small-scale problem-solving where the total number of variables to be considered is small and value problems restricted.”
In contrast, for large-scale real-world decision problems faced by most bureaucracies, Lindblom considers the rational-comprehensive approach in equation (1) to be impracticable because the net benefit or reward function R is not known or agreed to; choice set A may be too large to enumerate or search effectively, or unknown and costly to develop; and often no single centralized authority is capable of, authorized to, or accountable for identifying and implementing the best choice in A. Instead of clarifying values and objectives in advance, goals and actions to achieve them are selected together as opportunities arise. The test of a “good” policy is not that it is the best means to desired ends, or that it maximizes some measure of expected net benefit, utility, or collective welfare, but that people will agree to it (possibly for different, and perhaps conflicting, private reasons). Important possible outcomes, feasible alternative policies, and affected values and trade-offs are neglected in favor of relatively simple comparisons between the current policy and a proposed incremental modification of it. A succession of such modifications may, if all goes well, produce gradually improving policies; this is the process that Lindblom refers to as successive limited comparisons, or, more colloquially, as muddling through. He states that “Making policy is at best a very rough process. Neither social scientists, nor politicians, nor public administrators yet know enough about the social world to avoid repeated error in predicting the consequences of policy moves. A wise policy maker consequently expects that his policies will achieve only part of what he hopes and at the same time will produce unanticipated consequences that he would have preferred to avoid. If he proceeds through a succession of incremental changes, he avoids serious lasting mistakes in several ways” including learning from experience and being able to correct missteps fairly quickly. Of course, this view is optimistic if a single misstep could lead to disaster, ruin, or the destruction of the decision-making organizations, but Lindblom does not dwell on these grim possibilities. To model and evaluate the muddling through approach more formally, however, we will have to consider possibilities for safe learning, i.e., surviving and avoiding disastrous decisions during learning (Garcia & Fernandez, Reference Garcia and Fernandez2015). Lindblom proposes muddling through not only as a descriptive theory of bureaucratic decision-making, but also as a normative one: “Why then bother to describe the method in all of the above detail? Because it is in fact a common method of policy formulation and is, for complex problems, the principal reliance of administrators as well as of other policy analysts. And because it will be superior to any other decision-making method available for complex problems in many circumstances, certainly superior to a futile attempt at superhuman comprehensiveness.” In short, muddling through by successive incremental adjustments of policy is proposed as both more desirable and more widely practiced than the rational-comprehensive approach.
Since Lindblom’s essay, revolutions have occurred in computer science, game theory, collective choice theory, automated and adaptive control, artificial intelligence, robust optimization and risk analysis, machine learning, computational statistics and data science, and the intersection of these fields with political economy, law-and-economics, and management science. It is timely to reexamine the extent to which Lindblom’s critique of rational-comprehensive techniques for risk management decision support still applies; the extent to which the ferment of ideas and technical developments in artificial intelligence and other fields dealing with multiagent control has overcome his objections; how both the strengths and the limitations of muddling through can be understood better, and the technique applied more successfully, in light of progress since 1959; and whether there are circumstances in which muddling through provides a viable alternative or complement to decision analysis. The following sections undertake such a reexamination.
2 Developments in rational-comprehensive models of decision-making
An individual, team, organization, or artificial intelligence that repeatedly makes decisions to achieve some overall purposes or goals must repeatedly decide what to do next – e.g., what subgoals or tasks to undertake next – and how to do it, e.g., which agents should do what, and how much planning should be local and autonomous instead of centralized or hierarchical. In teams with no central coordinator, such as robot soccer teams of cooperating autonomous agents, cooperating swarms of drones, or search-and-rescue teams with autonomous agents and limited communication, the agents may have to infer and adapt to each other’s plans on the fly as they observe each other’s behaviors and messages (Hunt et al., Reference Hunt, Meng, Hinde and Huang2014; Zhao et al., Reference Zhao, Meng and Chung2016). In bureaucracies or other organizations where policies are formulated and adapted via muddling through, success or failure in achieving stated goals may depend on who may propose what, when, and how decisions are made about which proposals to adopt, and how these changes and their consequences are linked to incentives and rewards for those participating in policy-making and administration.
In the face of such complexities, the simple prescriptive model of optimization-based rational-comprehensive decision-making in (1) has been generalized and extended in the following ways.
Noncooperative game theory (Luce & Raiffa, Reference Luce and Raiffa1957) replaces the reward function R(a) in (1) with a set of reward functions (also called “payoff functions”), one for each participant (called a “player” or “agent”). Each player has its own choice set of feasible alternatives to choose among, often called strategies in game theory, or policies in decision analysis, machine learning, and artificial intelligence. Player i now seeks to choose ai from Ai to maximize Ri (ai , ai′ ), where ai denotes the strategy selected from Ai by player i; ai′ denotes all the strategies selected by the other players; and Ri (ai , ai′ ) is the reward to player i from choosing strategy ai when the other players choose ai′. There is no single net benefit, social welfare, or public interest to be maximized. Rather, each player seeks to act to maximize its own reward, given the actions of the rest. A Nash equilibrium is a set of choices such that no player can improve its own reward by unilaterally modifying its own choice, given the choices of the other players. Each player’s choice is a best response to the choices of the rest. A set of choices by the players is Pareto-efficient if no other set of choices would give all players equal or greater rewards, and at least to some of them greater rewards. In practical applications such as deciding how to manage air pollution, antibiotic resistance, or climate change, a common challenge is that each player benefits if everyone else exercises restraint to avoid making the current problem worse, but each player also maximizes its own benefits by being unrestrained itself, whatever the other players are doing. In such cases, the unique Nash equilibrium is that no one exercises self-restraint, even though all would gain if all would do so; hence, it is not Pareto-efficient. A variety of “folk theorems” of game theory prove that both Pareto efficiency and multiperiod versions of Nash equilibrium can be achieved if players are sufficiently patient (i.e., they do not discount delayed rewards too steeply) in repeated games with discounted rewards and uncertain time horizons, where the players have a chance to observe each other’s behaviors and make choices repeatedly over time. The trick is to have players make choices that punish those who do not cooperate in sustaining a Pareto-efficient outcome (Fudenberg & Maskin, Reference Fudenberg and Maskin1986; Fudenberg et al., Reference Fudenberg, Levine and Maskin1994; Hörner & Olszewski, Reference Hörner and Olszewski2006).
Cooperative game theory further generalizes the multiplayer choice problem by allowing players to form coalitions and to bargain or negotiate with each other. For example, in the treaty participation game model of international cooperation (or lack of it) to limit emissions in hopes of limiting undesired climate change, a coalition of signatories might choose emissions levels to maximize their collective benefits, while nonsignatories choose emission levels to maximize their individual benefits (Barrett, Reference Barrett2013). The final levels of cooperation and emissions achieved in multistage games of coalition formation and decision-making about emissions depend on factors such as whether coalitions, once formed, are exclusive; whether players (e.g., countries) can make and enforce conditional agreements such as that some will reduce their emissions more if and only if others do; whether binding commitments can be made and enforced; how steeply participants discount future rewards and penalties compared to current ones; and whether the timing of catastrophic consequences from failure to muster sufficient cooperation is known or uncertain (Heitzig et al., Reference Heitzig, Lessmann and Zou2011;Wood, Reference Wood2011; Barrett, Reference Barrett2013).
Team theory (Marschak & Radner, Reference Marschak and Radner1972) focuses on design of costly communication and agent decision rules (and, in some versions, on allocation of limited resources among the agents) for the special case of cooperating agents in an organization where all of the agents have identical preferences and goals. That is, they all seek to maximize the same reward function of their joint choices, but local observations, actions, and communications are costly. Team theory has been applied to distributed control of systems by agents with sensors and actuators at different locations, as well as to organizational design, design of compensation systems, and dynamic allocation of tasks, roles, and responsibilities within teams of cooperating agents.
Mechanism design: Institutions, social and moral norms, legal constraints and liabilities, regulations and their enforcement, wages and contractual incentives, outcome-sharing rules in principal-agent relationships and investment syndicates, and reputations in repeated transactions and long-term relationships all help to shape the rewards (positive or negative) and feedback that players receive for their choices and behaviors. Game theory studies how agents make choices in response to incentives. Mechanism design theory (Nisan, Reference Nisan, Nisan, Roughgarden, Tardos and Vazirani2007) studies the inverse problem of how to design incentives, or the rules determining rewards in the games in which agents participate, to elicit choices that satisfy desired properties. These may include Pareto efficiency, self-enforcing stability (e.g., Nash equilibrium and its multiperiod extensions), implementability using information that can actually be obtained and incentives (e.g., payments) that can actually be provided, and voluntary participation. Although important impossibility theorems show that successful mechanism design satisfying most or all of these properties is impossible if preferences are arbitrary, many positive results are available when preferences satisfy restrictions (e.g., risk neutrality and “quasi-linear preferences” with utility linear in money) commonly assumed in traditional benefit-cost analyses.
Organizational design and law-and-economics: Within bureaucracies and other hierarchical organizations (e.g., principal-agent relationships), as well as in the more specialized contexts of designing contracts and auctions, mechanism design can be applied to design incentive systems to promote revelation of local information, elicit desired behaviors despite private information, and optimize delegation and trade-offs between centralization and decentralization, taking into account costs of communication, monitoring, and control and inefficiencies due to remaining private information (Mookherjee, Reference Mookherjee2006). As a prominent application of the mechanism design perspective, the modern theory of law and economics (Miceli, Reference Miceli2017) explains how systems of laws establishing tort liability rules for hazardous activities, remedies for breach of contracts, property rights to internalize externalities, product liability and implicit warranty principles, and so forth can be designed to maximize the expected net economic benefit from voluntary transactions, usually assuming risk-neutral participants with quasi-linear preferences. Practical designs that explain many aspects of observed legal practice account for market imperfections such as private and asymmetric information (e.g., a consumer may not know how much care a manufacturer has taken to keep a product safe, or the manufacturer may not know how much care the consumer will exercise in using the product safely), costs of litigation, misperceptions of risk by buyers, and incentives for socially valuable research and disclosure of information by sellers.
3 Modern algorithms for single-and multiagent decision-making
The intersection of computer science with decision models and algorithms has tremendously advanced the design and practical application of algorithms for solving large-scale single-person and team decision optimization problems, as well as games and collective choice problems, in recent decades. Current state-of-the-art algorithms are briefly described next.
Monte Carlo Tree Search (MCTS). Decision trees and game trees showing possible sequences of actions (choice nodes) and uncertainty resolutions (chance nodes, with probabilities for each branch) leading to rewards (utilities) at the ends (leaf nodes) of the tree are perhaps the best known rational-comprehensive models of normative decision analysis for small problems (Raiffa, Reference Raiffa1968; Luce & Raiffa, Reference Luce and Raiffa1957). For large problems, recent MCTS algorithms (Munos, Reference Munos2014; Silver et al., Reference Silver, Huang, Maddison, Guez, Sifre, Driessche and Schrittwieser2016, Reference Silver, Hubert, Schrittwieser, Antonoglou, Lai, Guez and Lanctot2018) sample possible future paths and rewards to avoid enumerating all possibilities. This decouples “rational” decision-making, based on optimizing current decisions using predicted future reward probabilities, from “comprehensive” modeling of the causal relationship between choices and reward probabilities, by selecting only the most promising choice nodes in a tree for further simulation and evaluation. MCTS can be combined with reinforcement learning (RL) techniques discussed next (Vodopivec et al., Reference Vodopivec, Samothrakis and Ster2017) and applied to more general settings, such as those in which it is costly to observe the reward (Schulze & Evans, Reference Schulze and Evans2018), as is the case for many social policy interventions.
Reinforcement learning (RL) of high-reward policies through trial and error learning (Sutton & Barto, Reference Sutton and Barto1998, Reference Sutton and Barto2018). Decision-makers (agents) often initially do not know how their choices affect reward probabilities, or expected benefits, but must discover the immediate and longer-term costs and benefits of alternative policies or choices from experience. Denote true expected value starting in state s and acting optimally thereafter by an (initially unknown) value function, V(s) and let Q(a, s) denote an estimate of the value from taking each feasible action a when in each state s and then acting optimally (e.g., to maximize the discounted sum of future rewards) ever after. The initial estimates of these values may be random guesses, but they are updated in light of experience by adjusting current estimates by an amount proportional to the difference between expected and experienced rewards. The constant of proportionality is interpreted as the learning rate. For example, Q-learning uses the current estimate Q(a, s) to select which action to take next in the current state s. Then the resulting reward is used to update the estimate of Q(a, s) based on the difference between estimated and observed rewards. In many settings, estimated Q(a, s) values converge and the policy of selecting a to maximize Q(a, s) is then the optimal policy, while the estimated value of Q(a, s) when that policy is used is the true value function, V(s). This procedure is similar to value iteration in classical stochastic dynamic programming, but without the requirement that the reward function and state transition probabilities be initially known. It converges to yield optimal policies under certain conditions for Markov decision processes (MDPs), in which the actions taken affect next-state probabilities as well as probability distributions of current rewards (Krishnamurthy, Reference Krishnamurthy2015). The main conditions are that learning rates be kept small enough and that the MDPs are ergodic, involving no irreversible choices or fatal outcomes that would limit or prevent future exploration and adaptation (Bloembergen et al., Reference Bloembergen, Tuyls, Hennes and Kaisers2015; Krishnamurthy, Reference Krishnamurthy2015; Xu et al., Reference Xu, Qin, Wang and Liu2017).
RL using policy gradient algorithms. RL can also be based on algorithms that emphasize adjusting polices directly rather than estimating values for different actions as in benefit-cost analysis. As usual, a policy in RL is a decision rule mapping observations (e.g., the current state) to actions. In most RL algorithms, however, this mapping is randomized: thus, a policy RL specifies the probability of taking each feasible action when in each state (or, more generally, given current information, which may include imperfect observations of the current state). Polices are updated to favor selecting actions with higher expected values. The tension between exploring further in hopes of finding a more valuable policy and exploiting what has been learned so far by selecting the actions with the highest expected values is managed carefully by choosing action-selection probabilities to avoid premature convergence to suboptimal policies. For example, a simple and effective policy in many settings is to select each action with a probability equal to the currently estimated probability that it is the best (value-maximizing) action; this is called Thompson sampling (Schulze & Evans, Reference Schulze and Evans2018). Such randomized sampling schemes prevent jumping to possibly erroneous conclusions about what works best in clinical trials and similar sequential decision optimization settings (Villar et al., Reference Villar, Bowden and Wason2015). Adjustments of policies continue until expected and experienced average rewards no longer differ. For large classes of adaptive decision problems under uncertainty, the policies arrived at by such successive incremental adjustments are the optimal policies that would be obtained by classical operations research methods (Bloembergen et al., Reference Bloembergen, Tuyls, Hennes and Kaisers2015; Krishnamurthy, Reference Krishnamurthy2015; Xu et al., Reference Xu, Qin, Wang and Liu2017). Table 1 lists important refinements and enhancements used in practice to make RL quicker and more robust to data limitations. Table 2 summarizes methods for safe learning that have proved effective in applications ranging from learning to control helicopters and quadcopters (e.g., allowing them to hover or navigate safely in cluttered environments) to learning to manage power grids and other networked infrastructures, without risking costly accidents and failures during learning. Table 3 summarizes variations and extensions of multiagent reinforcement learning (MARL) in which multiple agents act, learn, and perhaps communicate about how to control a system or accomplish a task. MARL can greatly increase the speed of learning and average rewards generated per unit time, under certain conditions (Omidshafiei et al., Reference Omidshafiei, Pazis, Amato, How and Vian2017; Gupta et al., Reference Gupta, Egorov and Kochenderfer2017).
Table 1 Some enhancements to reinforcement learning (RL) algorithms.

Table 2 Some principles for safe learning, i.e., learning without risking catastrophic failures.

Table 3 Some MARL variations and extensions.
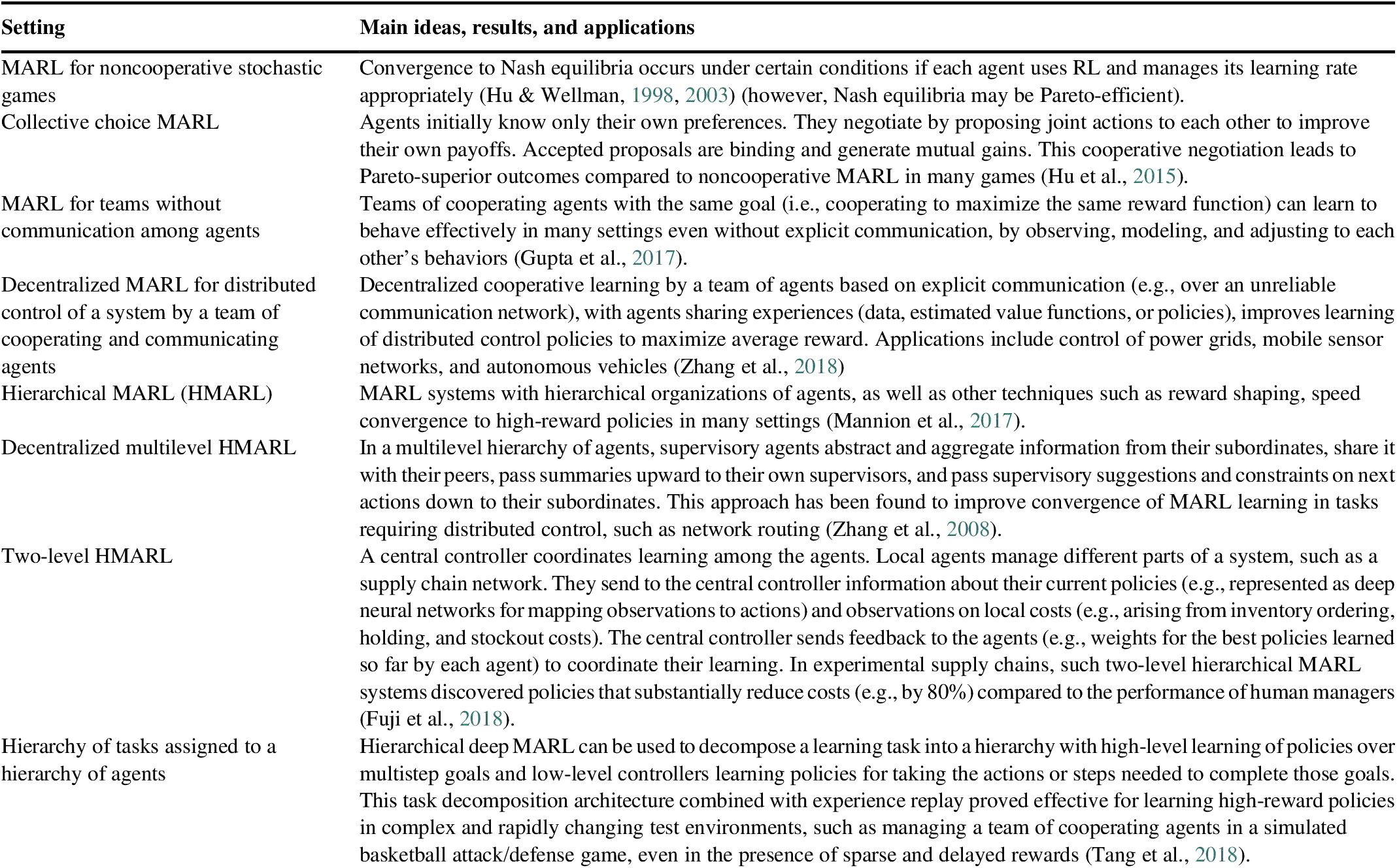
MARL algorithms and architectures that incorporate MCTS and enhancements to speed up convergence, safe learning, and communication and control hierarchies represent the current state of the art in machine learning models and methods for solving large-scale and distributed decision and control problems under uncertainty, including problems with sparse and delayed feedback. Although most MARL algorithms are designed for cooperating agents, Bowling and Veloso (Reference Bowling and Veloso2001) showed that convergence to Nash equilibria can also be achieved in a variety of noncooperative Markov games (generalizations of MDPs to multiple agents) if each agent uses RL but manages its learning rate to take large steps when the agent’s experienced rewards are less than expected (“learn fast when losing”) and small steps otherwise (when it is “winning” by receiving higher than expected rewards). The resulting WoLF (“win or learn fast”) principle has been incorporated into many subsequent MARL algorithms for cooperative learning. It gives agents who are lagging in learning to contribute to the team’s success time to catch up, while agents who are ahead of the rest continue to explore relatively cautiously (via relatively small incremental adjustment steps) for even better policies. In practice, MARL algorithms have been applied successfully to obtain high-reward policies for difficult distributed decision and control problems such as job shop scheduling among multiple agents (Gabel & Riedmiller, Reference Gabel and Riedmiller2007); coordination of military force attacks in increasingly large-scale and realistic war game simulations (e.g., StarCraft battles) (Usunier et al., Reference Usunier, Synnaeve, Lin and Chintala2016); and self-organizing control of swarms of drones to perform missions or to cooperate in choosing locations to obtain full visual coverage of a complex and initially unknown environment (Pham et al., Reference Pham, La, Feil-Seifer and Nefian2018). Safe MARL (SMARL) and Hierarchical MARL (HMARL) algorithms have demonstrated promising performance in controlling autonomous vehicles (Shalev-Shwartz et al., Reference Shalev-Shwartz, Shammah and Shashua2016) and teams of robots performing challenging tasks such as urban search and rescue in complex and uncertain environments (Cai et al., Reference Cai, Yang and Xu2013), respectively. Such results suggest the potential for MARL principles and their extensions to contribute to improved control of complex distributed systems in important practical business, military, and industrial engineering applications.
4 Discussion: implications of advances in rational-comprehensive decision theory for muddling through
A key insight from machine learning is that policy gradient algorithms and other RL and MARL techniques that take successive incremental steps guided by experience – and in this sense muddle through – end up solving dynamic optimization problems. This finding addresses the “rational” component of Lindblom’s critique by showing that muddling through and optimization are not opposed: muddling through provides one way to solve optimization problems. Likewise, RL’s ability to solve adaptive dynamic optimization problems without requiring initial knowledge of the optimization problems being solved – specifically of how different choices affect reward probabilities and next-state transition probabilities in dynamic systems or environments – renders the “comprehensive” knowledge requirement no longer necessary. Sampling-based approximate optimization algorithms such as MCTS further reduce the need for a comprehensive examination and evaluation of decision options. In short, rather than being thesis and antithesis, as Lindblom framed them, optimization and muddling through have undergone a useful synthesis in modern machine learning via RL and MARL.
However, fully automated RL and MARL techniques for quickly discovering optimal or near-optimal policies remain elusive. Computational complexity results for decentralized control of Markov decision processes (MDPs) and their generalizations suggest that some of these limitations are intrinsic for MARL (although not for single-agent RL with MDPs) (Papadimitriou & Tsitsiklis, Reference Papadimitriou and Tsitsiklis1985), and hence that discovery of high-reward policies will always be time-consuming unless there is some measure of centralized control (Bernstein et al., Reference Bernstein Daniel, Zilberstein and Immerman2000). Of course, real organizations do not simply implement computer science algorithms, and it would be simplistic to read into the complexities of human organizational design and behavior all the limitations (or only the limitations) of RL and MARL algorithms. Nonetheless, understanding how and why these algorithms fail in some settings suggests important pitfalls to avoid in organizations that rely on muddling through, insofar as they follow the same basic principles. Conversely, success factors that turn out to be necessary for effective RL or MARL machine learning of high-reward policies in relatively simple environments may help to suggest necessary (although not sufficient) conditions for effective organizational learning within and among human organizations. The following paragraphs summarize key lessons and some comparisons with observed real-world decision processes for human organizations.
1. Collect accurate, relevant feedback data and use it to improve policies.
After each new action is taken, RL evaluates the reward received and compares it to the reward that was expected so that the difference can be used to correct erroneous expectations and update the current policy. This requires that the effects of actions be evaluated and compared to prior expectations or predictions, and also that policies then be adjusted in light of the data. In the real world, policy-making and policy-administering bureaucracies frequently violate each of these requirements. For example, finding that investments in a costly course of action have yielded lower-than-expected returns may provoke those who originally chose it to escalate their commitment to it (Molden & Hui, Reference Molden and Hui2011; Schultze et al., Reference Schultze, Pfeiffer and Schulz-Hardt2012). Possible psychological and political explanations for escalating commitment range from loss aversion to seeking to manage the impressions of others, but clearly such resistance to modifying or abandoning previous choices in light of experience inhibits effective learning (Cox, Reference Cox2015; Tetlock & Gardner, Reference Tetlock and Gardner2015). In business as well as government, data needed to evaluate and compare actual to predicted performance of a policy are often not even collected, or are ignored or misinterpreted if they are collected (Russo & Schoemaker, Reference Russo and Schoemaker1989). In social policy application areas as diverse as education, criminal justice, and health care, changes in policy are often implemented without any clear predictions about expected changes in rewards or careful evaluations of actual changes in rewards (Tetlock & Gardner, Reference Tetlock and Gardner2015). These failures of design and analysis prevent the crucial learning from experience that is essential to effective muddling through. The remedy is to collect, retain, candidly communicate, and use accurate data on predicted and observed outcomes from implemented policies to improve them over time.
2. Explore via experiments to discover how to cause desired changes in outcome probabilities.
It is tempting for a policy analyst or policy maker steeped in the rational-comprehensive tradition criticized by Lindblom to create the best possible model of how one believes the world works and then to choose the action or policy that maximizes expected utility according to this model, as in equation (1). But in reality, the causal relationship between choices of policies and resulting conditional probabilities of different consequences and rewards is often initially highly uncertain. Prudent and effective policy-making requires acknowledging and coping with this model uncertainty, rather than selecting and using a single model. RL and MARL algorithms do this via randomized selection of actions (e.g., using Thompson sampling or other randomized sampling schemes) (Schulze & Evans, Reference Schulze and Evans2018) to discover which policies work best and to avoid becoming stuck in local optima, but it is counter-cultural among people who believe that one should know and not guess about the best course of action before taking it (Tetlock & Gardner, Reference Tetlock and Gardner2015), and among decision analysts who believe that one should solve an expected utility optimization problem and then make deterministic decisions based on the results. Neither belief fully acknowledges or responds constructively to the reality emphasized by Lindblom that current knowledge is often simply insufficient to permit confident identification of the best policy, and that experimentation is the only practical way to discover how to do better. Fortunately, the use of randomized controlled trials (RCTs) in social policy experimentation and evaluation of interventions has become increasingly accepted and practiced recently, in areas ranging from disrupting poverty (Tollefson, Reference Tollefson2015) to preventing delinquency (de Vries et al., Reference Vries, Hoeve, Asscher and Stams2018) to improving oral health of fifth grade students (Qadri et al., Reference Qadri, Alkilzy, Franze, Hoffmann and Splieth2018) to reducing child abuse by intervening with substance-abusing parents (Barlow et al., Reference Jane, Sembi, Parsons, Kim, Petrou, Harnett and Dawe2019). For collective learning and decision problems, such as controlling air pollution health effects, RCTs may not be practicable or ethical, but natural experiments and quasi-experiments provide valuable opportunities to learn from observed responses to unplanned or nonrandom interventions (Boogaard et al., Reference Hanna, Erp, Walker and Shaikh2017; Henneman et al., Reference Henneman, Liu, Mulholland and Russell2017).
3. During collective learning, agents should advance slowly when doing better than expected, but retreat quickly when doing worse.
The “win or lose fast” (WoLF) principle from MARL provides a useful heuristic for coordinating the rates at which agents on a team adjust their individual policies to prevent collective instability, so that they can eventually find and exploit a coordinated set of individual policies for maximizing team reward. In practice, destabilized policy-making processes in human organizations can manifest as “policy churn,” in which new policies are proposed before old ones are well implemented and evaluated by the teams of agents implementing them (Monios, Reference Monios2016). Teachers implementing education reform programs; bankers implementing new risk management regulations and requirements; medical staff implementing new infection control protocols in hospital wards; and workers in bureaucracies implementing policy changes have all been frustrated by policy churn that encourages costly activity and change without providing the opportunities for careful and thorough evaluation and improvement needed to improve outcomes. Perhaps fear of constant deflections and the resulting lack of progress explains some of the previously discussed reluctance to systematically collect and use feedback data to evaluate and improve policies. Conversely, the desire to show action and strong leadership, or to obscure the results of previous ineffective choices, might provide incentives for policy churn. In any case, the study of RL and MARL performance suggests that deliberately controlling step sizes and adjustment rates for policy updates might facilitate productive incorporation of feedback data into policy updates for a group of cooperating agents without destabilizing their learning and improvement process.
4. Separate actors and critics.
The RL idealization of frequent small adjustments made without significant costs, delays, or uncertainties in implementation is too simple to describe most real-world decision processes. Nonetheless, some RL and MARL principles may still be useful for human organizations. One of the most useful may be that decision and evaluation of decision performance should be kept distinct processes. Reasons abound in individual and group psychology for keeping those who make decisions about policy adjustments (analogous to “actors” in actor-critic RL algorithms) separate from those who evaluate the performance of the policies and provide feedback and suggestions for improving them (the “critics”). Among these reasons are confirmation bias, motivated reasoning, groupthink, and other heuristics and biases (Cox, Reference Cox2015). RL suggests an additional reason, rooted in statistics: in deep learning RL algorithms, training one network to decide what to do next and a separate one to evaluate how well it is working has been found to prevent overly optimistic assessments of policy performance due to overfitting, i.e., using the same data to both select estimated value-maximizing actions and estimate the values from taking those actions (van Hesselt et al., Reference Hesselt, Guez and Silver2015). The principle of separating the processes for choosing which changes to make and evaluating how well they perform can also be applied usefully to choice of learning rates (i.e., choosing how much to modify current policies in light of feedback) as well as to choice of policies (Xu et al., Reference Xu, Qin, Wang and Liu2017). Possible future advances include deliberately diversifying the learning rates of different agents on the same team to obtain the advantages of both rapid exploration of new policies and thorough exploitation and refinement of old ones. This is an old concept in organizational science (e.g., March, Reference March1991), but is still being developed in MARL research (Potter et al., Reference Potter, Meeden and Schultz2001).As a practical matter, separation of actors and critics can be applied fruitfully to major social learning and improvement initiatives, such as air pollution regulation, through accountability studies that revisit previous regulatory actions or other decisions to assess their results (Boogaard et al., Reference Hanna, Erp, Walker and Shaikh2017; Henneman et al., Reference Henneman, Liu, Mulholland and Russell2017). Use of such evaluation studies to evaluate and update previous policy decisions – ideally, in time to be useful in guiding policy decisions elsewhere – is clearly consistent with the principle of collecting and using relevant feedback data. Separation of actors and critics provides an additional principle for using feedback data to maximum advantage to improve polices and their results.
5. Shape rewards to promote learning and improvement.
Recently, it has been found that using causal (counterfactual) models to shape each agent’s reward to reflect the estimated difference it has made – the difference between what was actually achieved and what would have been expected without each agent’s contribution, or its marginal value, in microeconomic terms – can speed collective learning and optimization when each agent seeks to maximize its own reward (Devlin et al., Reference Devlin, Yliniemi, Kudenko and Tumer2014). This research uses mathematical rewards that are costless to implement, so that budget constraints such as that the sum of agent rewards must not exceed the collective reward of the team, do not apply. However, it seems plausible that, even in the presence of budget constraints, rewarding each agent according to its estimated marginal contribution (or its expected marginal contributions, or Shapley values in game theory) might promote joint learning about how to contribute more effectively, as well as having other properties of efficiency and fairness familiar from microeconomics and game theory. Of course, the asymmetric information about relative roles of chance and effort typical in principal-agent problems can inhibit accurate reward shaping in practice, and causal modeling of individual marginal contributions to team performance is challenging. Nonetheless, research on how best to use reward shaping to provide feedback and encourage effective learning, as well as to create incentives, may be useful for human organizations as well as for MARL algorithms.
6. Learn from the experiences and expertise of others.
Learning from each other by sharing valuable memories, experiences, and expertise (typically encoded as causal models or trained neural nets) helps teams of MARL agents discover high-reward joint policies for controlling large-scale systems and accomplishing tasks in complex, changing, uncertain environments. In applying such ideas to human organizations, it is valuable to recognize that the “agents” may themselves be organizations, such as different schools, hospitals, or companies; or similar government bureaucracies in different states or countries. States and counties implementing pollution-reducing regulations might learn from each other’s experiences about which combinations of interventions and conditions (possibly involving copollutants, weather variables, and sociodemographic characteristics of the exposed population) generate the greatest public health benefits from pollution reduction measures. As usual, effective learning in human organizations must overcome challenges from various types of learning aversion that have no clear counterparts in machine learning (Cox, Reference Cox2015). For example, human bureaucracies may reorganize to visibly mimic organizational structures in more successful organizations whose reputations they covet, but without corresponding learning of the more effective policies that drive improved performance (Monios, Reference Monios2016). Players preoccupied with managing the perceptions and impressions of others to shape allocations of collective efforts and rewards to their own individual advantages may be unable to achieve Pareto efficiency or to maximize any measure of collective success or reward. These threats do not arise for teams of agents trying to cooperate in maximizing the same reward function. Our recommendation that agents should learn from each other in order to speed mastery of joint policies for obtaining high rewards from the environment is primarily applicable to such teams of cooperating agents.
5 Conclusions
In 1973, two professors of design and city planning offered the following sober assessment of the prospects for scientifically based social policy:
“The search for scientific bases for confronting problems of social policy is bound to fail, because of the nature of these problems. They are ‘wicked’ problems, whereas science has developed to deal with ‘tame’ problems. Policy problems cannot be definitively described. Moreover, in a pluralistic society there is nothing like the undisputable public good; there is no objective definition of equity; policies that respond to social problems cannot be meaningfully correct or false; and it makes no sense to talk about ‘optimal solutions’ to social problems unless severe qualifications are imposed first. Even worse, there are no ‘solutions’ in the sense of definitive and objective answers.” (Rittel & Webber Reference Rittel and Webber1973)
We believe that subsequent developments warrant greater optimism. While it is true that sufficiently heterogeneous preferences may make it impracticable or impossible to define and measure a single indisputable public good to be optimized, it is also true that agents with at least some shared goals have already achieved impressive feats of cooperation and control using MARL principles, in applications as diverse as autonomous vehicle fleet and drone swarm control, search-and-rescue via teams of cooperating autonomous robots, distributed management of supply chains, and military gaming. Such applications are admittedly far less difficult than the wicked problems referred to by Rittel and Webber, but many of the differences are of scale rather than of kind: robot teams are already using RL, MARL, and HMARL to confront, with increasing competence, the difficulties of distributed decision-making with initially unclear roles and priorities, uncertain and changing environments, opportunistic revision of goals and plans, and local information that may be time consuming and expensive to share. Multiple practical applications have demonstrated the advantages of improving via small steps rather than trying to optimize in one big decision, and this insight from Lindblom’s 1959 paper remains true for machine learning as well human organizations. It has been augmented by the discovery that successive incremental improvement based on feedback at each step and careful selection of step sizes is often an effective way to solve dynamic optimization problems when they can be clearly formulated, as well as an effective way to learn how to act when not enough is initially known to formulate a clear decision optimization problem.
As artificial intelligence and machine learning algorithms are tested and improved on increasingly challenging tasks, principles for learning how to manage risks and act effectively in a variety of centralized, decentralized, and hierarchical organizational structures have begun to emerge. We have discussed several based on recent work that uses deep neural networks to approximate value functions in RL, MARL, and HMARL algorithms. These principles are only the beginning of what may soon become a substantial flow from multi agent machine learning to human management science of useful principles for improving organizational design and performance in coping with realistically complex and uncertain collective decision and policy improvement challenges. These principles will doubtless require modifications and extensions for the human world, since human psychology for both individuals and groups differs greatly from RL and MARL agent programming. But the pace of discovery and progress in using machine learning to solve increasingly large, difficult, and important real-world problems of decision-making under uncertainty is now extremely rapid. Discovering how groups and teams of agents can organize, learn, decide, and adapt more effectively is becoming an experimental and applied science, as well as a theoretical one, in current artificial intelligence and machine learning. It seems likely that this research will produce insights and principles to help tame currently wicked problems and develop increasingly effective and beneficial polices in collective choice applications with high stakes for humans.
Acknowledgments:
I thank Vicki Bier and Warner North for valuable comments on an early draft that improved the framing, content and exposition in this paper. I thank Susan Dudley for inviting me to prepare a paper and presentation for panel discussion at the Society for Risk Analysis (SRA) 2018 Annual Meeting, with partial support from the Searle Foundation. This paper reflects the enthusiastic comments and suggestions of organizers and participants in the SRA session. I am grateful for the opportunity to share, discuss, and improve these ideas.





