Research Papers
Availability of periodically inspected systems with Markovian wear and shocks
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 303-317
-
- Article
-
- You have access
- Export citation
Average optimality for Markov decision processes in borel spaces: a new condition and approach
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 318-334
-
- Article
-
- You have access
- Export citation
Boundedly rational quasi-Bayesian learning in coordination games with imperfect monitoring
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 335-350
-
- Article
-
- You have access
- Export citation
Structured coalescent with nonconservative migration
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 351-362
-
- Article
-
- You have access
- Export citation
On the value function of the M/Cox(r)/1 queue
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 363-376
-
- Article
-
- You have access
- Export citation
Limit distribution of distances in biased random tries
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 377-390
-
- Article
-
- You have access
- Export citation
Hazard rate ordering of order statistics and systems
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 391-408
-
- Article
-
- You have access
- Export citation
A central limit property under a modified Ehrenfest urn design
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 409-420
-
- Article
-
- You have access
- Export citation
On a random-coefficient AR(1) process with heavy-tailed renewal switching coefficient and heavy-tailed noise
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 421-440
-
- Article
-
- You have access
- Export citation
Stationary-increment Student and variance-gamma processes
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 441-453
-
- Article
-
- You have access
- Export citation
An optimal sequential procedure for a buying-selling problem with independent observations
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 454-462
-
- Article
-
- You have access
- Export citation
Rare events, temporal dependence, and the extremal index
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 463-485
-
- Article
-
- You have access
- Export citation
A monotonicity in reversible Markov chains
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 486-499
-
- Article
-
- You have access
- Export citation
On the time behaviour of Okazaki fragments
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 500-509
-
- Article
-
- You have access
- Export citation
Moments of a Markov-modulated, irreducible network of fluid queues
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 510-522
-
- Article
-
- You have access
- Export citation
On the nonoptimality of the foreground-background discipline for IMRL service times
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 523-534
-
- Article
-
- You have access
- Export citation
On the infinite-horizon probability of (non)ruin for integer-valued claims
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 535-551
-
- Article
-
- You have access
- Export citation
Percolation in the signal to interference ratio graph
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 552-562
-
- Article
-
- You have access
- Export citation
Limiting dependence structures for tail events, with applications to credit derivatives
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 563-586
-
- Article
-
- You have access
- Export citation
Short Communications
Tail behavior of negatively associated heavy-tailed sums
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 587-593
-
- Article
-
- You have access
- Export citation



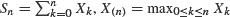 , and
, and