Hostname: page-component-848d4c4894-r5zm4 Total loading time: 0 Render date: 2024-06-21T10:51:54.285Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability of extremes with random sample size

Published online by Cambridge University Press:  14 July 2016

W. J. Voorn
W. J. Voorn*
Affiliation:
Universiteit van Amsterdam
*
∗ Postal address: Universiteit van Amsterdam, Vakgroep Medische Fysica, Meibergdreef 15, 1105 AZ Amsterdam, The Netherlands.
Get access Rights & Permissions [Opens in a new window]

Abstract

A non-degenerate distribution function F is called maximum stable with random sample size if there exist positive integer random variables Nn, n = 1, 2, ···, with P(Nn = 1) less than 1 and tending to 1 as n → ∞ and such that F and the distribution function of the maximum value of Nn independent observations from F (and independent of Nn) are of the same type for every index n. By proving the converse of an earlier result of the author, it is shown that the set of all maximum stable distribution functions with random sample size consists of all distribution functions F satisfying 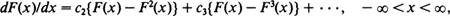where c2, c3, · ·· are arbitrary non-negative constants with 0 < c2 + c3 + · ·· <∞, and all distribution functions G and H defined by F(x)= G(c + exp(x)) and F(x) = H(c – exp(–x)), –∞ < x <∞, where c is an arbitrary real constant.

Keywords

LOGISTIC DISTRIBUTIONLOGLOGISTIC DISTRIBUTIONGEOMETRIC DISTRIBUTIONMAXIMAL TERMMIXTURES
Type
Research Papers
Information
Journal of Applied Probability , Volume 26 , Issue 4 , December 1989 , pp. 734 - 743
Copyright
Copyright © Applied Probability Trust 1989 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baringhaus, L. (1980) Eine simultane Charakterisierung der geometrischen Verteilung und der logistischen Verteilung. Metrika 27, 243–253.Google Scholar
Gnedenko, B. V. (1982) On some stability theorems. In Stability Problems for Stochastic Models. Proc. 6th Seminar, Moscow, eds. Kalashnikov, V. V. and Zolotarev, V. M., Lecture Notes in Mathematics 982, Springer-Verlag, Berlin, 24–31.Google Scholar
Kakosyan, A. V., Klebanov, L. B. and Melamed, J. A. (1984) Characterization of Distributions by the Method of Monotone Operators. Lecture Notes in Mathematics 1088, Springer-Verlag, Berlin.Google Scholar
Voorn, W. J. (1987) Characterization of the logistic and loglogistic distributions by extreme value related stability with random sample size. J. Appl. Prob. 24, 838–851.Google Scholar