Hostname: page-component-848d4c4894-jbqgn Total loading time: 0 Render date: 2024-06-25T05:32:14.176Z Has data issue: false hasContentIssue false
  • English
  • Français

A piecewise Markovian model for simulated annealing with stochastic cooling schedules

Part of: Markov processes Stochastic processes

Published online by Cambridge University Press:  14 July 2016

M. Kolonko
M. Kolonko*
Affiliation:
Universität Hildesheim
*
∗Postal address: Institut für Mathematik, Universität Hildesheim, Marienburger Platz 22, D-31141 Hildesheim, Germany
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce a stochastic process with discrete time and countable state space that is governed by a sequence of Markov matrices 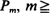. Each Pm is used for a random number of steps Tm and is then replaced by Pm+1. Tm is a randomized stopping time that may depend on the most recent part of the state history. Thus the global character of the process is non-Markovian.

This process can be used to model the well-known simulated annealing optimization algorithm with randomized, partly state depending cooling schedules. Generalizing the concept of strong stationary times (Aldous and Diaconis [1]) we are able to show the existence of optimal schedules and to prove some desirable properties. This result is mainly of theoretical interest as the proofs do not yield an explicit algorithm to construct the optimal schedules.

Keywords

INHOMOGENEOUS MARKOV CHAINSSEMI-REGENERATIVE PROCESSESSTRONG STATIONARY TIMES

MSC classification

Primary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Secondary: 60G40: Stopping times; optimal stopping problems; gambling theory
Type
Research Papers
Information
Journal of Applied Probability , Volume 32 , Issue 3 , September 1995 , pp. 649 - 658
Copyright
Copyright © Applied Probability Trust 1995 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Aldous, D. and Diaconis, P. (1987) Strong uniform times and finite random walks. Adv. Appl. Math. 8, 69–97.Google Scholar
[2] Anily, S. and Federgruen, A. (1987) Simulated annealing methods with general acceptance probabilities. J Appl. Prob. 24, 657–667.CrossRefGoogle Scholar
[3] Cerny, V. (1985) Thermodynamical approach to the travelling salesman problem: an efficient simulation algorithm. JOTA 45, 41–51.CrossRefGoogle Scholar
[4] ÇlInlar, E. (1975) Introduction to Stochastic Processes. Prentice-Hall, Englewood Cliffs, NJ.Google Scholar
[5] Geman, D. and Geman, S. (1987) Relaxation and annealing with constraints. Complex Systems Technical Report No. 35, Div. of Applied Mathematics, Brown University, Providence, RI 02912.Google Scholar
[6] Gidas, B. (1985) Non-stationary Markov chains and convergence of the annealing algorithm. J. Statist. Phys. 39, 73–131.Google Scholar
[7] Greene, J. W. and Supowit, K. J. (1986) Simulated annealing without rejecting moves. IEEE Trans. CAD 5, 221–228.CrossRefGoogle Scholar
[8] Hajek, B, (1988) Cooling schedules for optimal annealing. Math. Operat. Res. 13, 311–329.Google Scholar
[9] Kirkpatrick, S. and Gelatt, C. D. Jr. (1983) Optimization by simulated annealing. Science 220, No. 4598, 671–680.Google Scholar
[10] Kolonko, M. (1994) A piecewise Markovian model for simulated annealing with stochastic cooling schedule. Technical Report, Universität Hildesheim. Unabridged version of the present paper.Google Scholar
[11] Van Laarhoven, P. J. M. and Aarts, E. H. L. (1987) Simulated Annealing: Theory and Applications. Reidel, Dordrecht.Google Scholar
[12] Lundy, M. and Mees, A. (1986) Convergence of an annealing algorithm. Math. Progr. 34, 111–124.Google Scholar
[13] Mitra, D., Romeo, F. and Sangiovanni-Vincentelli, A. (1986) Convergence and finite-time behaviour of simulated annealing. Adv. Appl. Prob. 18, 747–771.Google Scholar
[14] Pitman, J. W. and Speed, T. P. (1973) A note on random times. Stoch. Proc. Appl. 1, 369–374.Google Scholar
[15] Ripley, B. D. (1987) Stochastic Simulation. Wiley, New York.Google Scholar
[16] Shahookar, K. and Mazumder, P. (1991) VLSI cell placement techniques. ACM Computing Surveys 23, 143–220.Google Scholar