Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-25T01:55:20.501Z Has data issue: false hasContentIssue false
  • English
  • Français

Percolation of coalescing random walks

Published online by Cambridge University Press:  14 July 2016

Bao Gia Nguyen
Bao Gia Nguyen*
Affiliation:
Illinois Institute of Technology
*
∗Postal address: Department of Mathematics, Illinois Institute of Technology, Chicago, IL 60616, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the shape of the binary tree containing 0 that is created from percolation of coalescing random walks. The key result is a duality lemma describing the shape of the tree. Furthermore, we show that 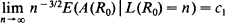and 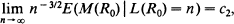where A(R0), M(R0), L(R0) are respectively the area, the number of external nodes and the length of the longest path of the tree R0.

Keywords

DUALITYCONDITIONED LIMIT THEOREM
Type
Research Papers
Information
Journal of Applied Probability , Volume 27 , Issue 2 , June 1990 , pp. 269 - 277
Copyright
Copyright © Applied Probability Trust 1990 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Belkin, B. (1970) A limit theorem for conditioned recurrent random walk attracted to a stable law. Ann. Math. Statist. 41, 146–163.CrossRefGoogle Scholar
Billingsley, P. (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
Durrett, R. (1984) Oriented percolation in two dimensions. Ann. Prob. 12, 1231–1271.Google Scholar
Feller, W. (1966) An Introduction to Probability Theory and Its Applications, Vol. II. Wiley, New York.Google Scholar
Hack, J. T. (1957) Studies of longitudinal stream profiles in Virginia and Maryland. US Geol. Surv. Prof. Paper 294B, B45–B97.Google Scholar
Ito, K. and Mckean, H. P. Jr. (1965) Diffusion Processes and Sample Paths. Springer-Verlag, Berlin.Google Scholar
Kaigh, W. D. (1975a) A conditional local limit theorem for recurrent random walk. Ann. Prob. 3, 882–887.CrossRefGoogle Scholar
Kaigh, W. D. (1975b) An invariance principle for random walk conditioned by a late return to zero. Ann. Prob. 4, 115–121.Google Scholar
Kesten, H. (1963) Ratio theorems for random walks II. J. Analyse Math. 9, 323–379.Google Scholar
Kesten, H. (1987) Percolation theory and first-passage percolation. Ann. Prob. 15, 1231–1271.Google Scholar
Leopold, L. B., and Langbein, W. B. (1962) The concept of entropy in landscape evolution. US Geol. Surv. Prof. Paper 500A, A1–A20.Google Scholar
Mesa, O. J. and Gupta, V. K. (1987) On the main channel length-area relationship for channel network. Water Resources. Res. 23, 2119–2122.Google Scholar
Mueller, J. E. (1973) Reevaluation of the relationship of master streams and drainage basins. Geol. Soc. Am. Bul. 83, 3471–3473.CrossRefGoogle Scholar
Spitzer, F. (1960) A Tauberian theorem and its probability interpretation. Trans. Amer. Math. Soc. 94, 150–169.Google Scholar
Stevens, P. S. (1974) Patterns in Nature. Little, Brown & Co. Boston.Google Scholar
Waymire, E. (1988) On the main channel length-area, formula for random networks: A solution to Moon's conjecture. Preprint.Google Scholar