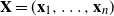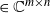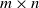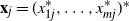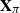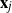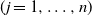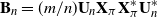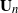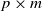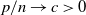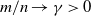1. Introduction
In multivariate statistical analysis, the sample covariance matrix is an extremely important statistic; see [Reference Anderson1] for more details. Its spectral properties serve as a fundamental theoretical underpinning for principal component analysis [Reference Jolliffe17]. In situations where the population size remains ‘small’ while the sample size becomes sufficiently large, the spectral properties are well understood. Classical probability outcomes reveal that the sample covariance matrix is a good approximation of the population one. However, when both sample and population sizes escalate indefinitely, this is not the case. Consequently, modern statistics urgently require a more robust theoretical framework, possibly with the constraint that their aspect ratio
![]() $c_n \;:\!=\; p/n$
approaches a finite limit
$c_n \;:\!=\; p/n$
approaches a finite limit
![]() $c \in (0, \infty)$
. In this context, the asymptotic spectral properties of the sample covariance matrix have garnered increasing attention in recent years, initiated by [Reference Marčenko and Pastur21] and further developed by [Reference Bai and Yin4, Reference Jonsson18, Reference Wachter26, Reference Yin29]. Extensive research has been carried out on models with a general population covariance; see, e.g., [Reference Silverstein22, Reference Silverstein and Bai24, Reference Silverstein and Choi25] for references.
$c \in (0, \infty)$
. In this context, the asymptotic spectral properties of the sample covariance matrix have garnered increasing attention in recent years, initiated by [Reference Marčenko and Pastur21] and further developed by [Reference Bai and Yin4, Reference Jonsson18, Reference Wachter26, Reference Yin29]. Extensive research has been carried out on models with a general population covariance; see, e.g., [Reference Silverstein22, Reference Silverstein and Bai24, Reference Silverstein and Choi25] for references.
To make the following discussions precise, we detail some notation.
Definition 1. Let
![]() $\textbf{A}$
be a
$\textbf{A}$
be a
![]() $p \times p$
Hermitian matrix, and denote its real eigenvalues by
$p \times p$
Hermitian matrix, and denote its real eigenvalues by
![]() ${\lambda_i}(\textbf{A})$
,
${\lambda_i}(\textbf{A})$
,
![]() $i = 1,2, \ldots, p$
. Then, the empirical spectral distribution (ESD) of
$i = 1,2, \ldots, p$
. Then, the empirical spectral distribution (ESD) of
![]() $\textbf{A}$
is defined by
$\textbf{A}$
is defined by
![]() $F^{\textbf{A}}(x) = ({1}/{p})\sum_{i = 1}^p{1({\lambda _i}(\textbf{A}) \le x)}$
, where 1(A) is the indicator function of an event A.
$F^{\textbf{A}}(x) = ({1}/{p})\sum_{i = 1}^p{1({\lambda _i}(\textbf{A}) \le x)}$
, where 1(A) is the indicator function of an event A.
Definition 2. If G(x) is a function of bounded variation on the real line, then its Stieltjes transform is defined by
where
![]() $z = u + {\mathrm{i}} v\in\mathbb{C}^+$
. Further, the Stieltjes transform of
$z = u + {\mathrm{i}} v\in\mathbb{C}^+$
. Further, the Stieltjes transform of
![]() ${F^{\textbf A}}(x)$
, which is the ESD of a
${F^{\textbf A}}(x)$
, which is the ESD of a
![]() $p \times p$
Hermitian matrix
$p \times p$
Hermitian matrix
![]() $\textbf{A}$
, is given by
$\textbf{A}$
, is given by
where
![]() $\textbf{I}_p$
is the identity matrix.
$\textbf{I}_p$
is the identity matrix.
Remark 1. For more details on the Stieltjes transform, we refer the reader to [Reference Geronimo and Hill13, Reference Silverstein23] and references therein.
We briefly review some relevant theoretical background here. Assume
![]() $\textbf{w}_j = \boldsymbol{\Sigma}_n^{1/2}\textbf v_j$
,
$\textbf{w}_j = \boldsymbol{\Sigma}_n^{1/2}\textbf v_j$
,
![]() $1\leq j\leq n$
, where
$1\leq j\leq n$
, where
![]() $\boldsymbol{\Sigma}_n^{1/2}$
is the square root of the non-negative definite Hermitian matrix
$\boldsymbol{\Sigma}_n^{1/2}$
is the square root of the non-negative definite Hermitian matrix
![]() $\boldsymbol{\Sigma}_n$
, and
$\boldsymbol{\Sigma}_n$
, and
![]() $\textbf V_n =(\textbf v_1, \textbf v_2, \ldots, \textbf v_n)$
is a
$\textbf V_n =(\textbf v_1, \textbf v_2, \ldots, \textbf v_n)$
is a
![]() $p\times n$
matrix. Its elements are independent and identically distributed (i.i.d.) complex random variables with zero means and unit variances. When
$p\times n$
matrix. Its elements are independent and identically distributed (i.i.d.) complex random variables with zero means and unit variances. When
![]() $p, n\to \infty$
,
$p, n\to \infty$
,
![]() $p/n\to c\in(0, \infty)$
, the ESD
$p/n\to c\in(0, \infty)$
, the ESD
![]() $F^{\boldsymbol{\Sigma}_n}$
of
$F^{\boldsymbol{\Sigma}_n}$
of
![]() $\boldsymbol{\Sigma}_n$
tends to a non-random probability distribution H, and the sequence
$\boldsymbol{\Sigma}_n$
tends to a non-random probability distribution H, and the sequence
![]() $\boldsymbol{\Sigma}_n$
is bounded in spectral norm. Then, the limiting spectral distribution (LSD) of the sample covariance matrix has been well studied in [Reference Silverstein22, Reference Silverstein and Bai24]. The theory states that with probability 1, the ESD
$\boldsymbol{\Sigma}_n$
is bounded in spectral norm. Then, the limiting spectral distribution (LSD) of the sample covariance matrix has been well studied in [Reference Silverstein22, Reference Silverstein and Bai24]. The theory states that with probability 1, the ESD
![]() $F^{\textbf S_n}$
of the sample covariance matrix
$F^{\textbf S_n}$
of the sample covariance matrix
![]() $\textbf S_n=({1}/{n})\sum^{n}_{j}\textbf{w}_j\textbf{w}_j^* =({1}/{n})\boldsymbol{\Sigma}_n^{1/2}\textbf V_n \textbf V_n^*\boldsymbol{\Sigma}_n^{1/2}$
weakly converges to a non-random distribution F as
$\textbf S_n=({1}/{n})\sum^{n}_{j}\textbf{w}_j\textbf{w}_j^* =({1}/{n})\boldsymbol{\Sigma}_n^{1/2}\textbf V_n \textbf V_n^*\boldsymbol{\Sigma}_n^{1/2}$
weakly converges to a non-random distribution F as
![]() $n \to \infty$
. Here,
$n \to \infty$
. Here,
![]() $\textbf W_n^*$
and
$\textbf W_n^*$
and
![]() $\textbf V_n^*$
are the conjugate transpose of matrices
$\textbf V_n^*$
are the conjugate transpose of matrices
![]() $\textbf W_n$
and
$\textbf W_n$
and
![]() $\textbf V_n$
, respectively. For each
$\textbf V_n$
, respectively. For each
![]() $z \in \mathbb{C}^+= \{u + {\mathrm{i}} v\colon v>0\}$
,
$z \in \mathbb{C}^+= \{u + {\mathrm{i}} v\colon v>0\}$
,
![]() $s(z) = s_F(z)$
is the unique solution to the equation
$s(z) = s_F(z)$
is the unique solution to the equation
in the set
![]() $\{s(z)\in\mathbb{C}\colon-(1-c)/z + cs(z)\in\mathbb{C}^+\}$
, where
$\{s(z)\in\mathbb{C}\colon-(1-c)/z + cs(z)\in\mathbb{C}^+\}$
, where
![]() $s_F(z)$
is defined as the Stieltjes transform of F. For more details, we refer the reader to [Reference Bai and Silverstein3, Reference Couillet and Debbah10, Reference Yao, Zheng and Bai28] for references.
$s_F(z)$
is defined as the Stieltjes transform of F. For more details, we refer the reader to [Reference Bai and Silverstein3, Reference Couillet and Debbah10, Reference Yao, Zheng and Bai28] for references.
In the fields of biology and finance, high-dimensional data with very small sample sizes are common. The permutation approach is an elegant technique in non-parametric statistics dating back to Fisher’s permutation test [Reference Fisher12]. The basic consideration is that permuting the observations of a sample preserves the magnitude of the sample (i.e. keeps sample moments of all orders invariant) while weakening the dependence between observations. Therefore, by comparing the statistics based on the original sample with that based on the permuted sample, we can find whether the original sample contains the assumed information. The permutation approach has been widely used for recovering data permutations from noisy observations [Reference Jeong, Dytso and Cardone16, Reference Ma, Cai and Li20], permutation parallel analysis for selecting the number of factors and principal components [Reference Buja and Eyuboglu7, Reference Dobriban11], and so on. Given these considerations, the sample covariance matrix of permuted samples may be of particular interest within the field of random matrix theory. In this paper, our exploration is centered around this compelling matter: the LSD of eigenvalues of random permutation matrices. An investigation into the limiting properties of large-dimensional random permutation matrices can instigate new challenges for classical statistical theory and propel the progression of large-dimensional random matrix theory
In what follows, we are ready to propose our model. We reprocess the raw data and divide the process into the following three steps. First, suppose that the raw data sample
![]() $\textbf z_1, \ldots, \textbf z_n$
$\textbf z_1, \ldots, \textbf z_n$
![]() $ \in \mathbb{C} ^m$
, where
$ \in \mathbb{C} ^m$
, where
![]() $\textbf z_j = (z_{1j}^{*}, \ldots, z_{mj}^{*} )^{*}$
,
$\textbf z_j = (z_{1j}^{*}, \ldots, z_{mj}^{*} )^{*}$
,
![]() $j=1, \ldots, n$
. Then, we centralize the raw data sample. Let
$j=1, \ldots, n$
. Then, we centralize the raw data sample. Let
![]() $\tilde{\textbf z}_j = \textbf z_j-\bar{z}_j \cdot \textbf{1}$
, where
$\tilde{\textbf z}_j = \textbf z_j-\bar{z}_j \cdot \textbf{1}$
, where
![]() $\textbf{1}= (1, \ldots , 1)^{*}$
denotes the m-dimensional vector of ones and
$\textbf{1}= (1, \ldots , 1)^{*}$
denotes the m-dimensional vector of ones and
![]() $\bar{ z}_j = ({1}/{m}) \sum_{i=1}^{m} z_{ij}$
. Accordingly,
$\bar{ z}_j = ({1}/{m}) \sum_{i=1}^{m} z_{ij}$
. Accordingly,
![]() $\tilde{z}_{ij} = z_{ij}-\bar{z}_j$
. Second, we further standardize the sample by letting
$\tilde{z}_{ij} = z_{ij}-\bar{z}_j$
. Second, we further standardize the sample by letting
 \begin{align*}x_{ij} = \frac{\tilde{z}_{ij}}{\sqrt{\sum_{i=1}^{m} \vert z_{ij} - \bar{z}_j \vert^{2}}\,} =\frac{z_{ij}-\bar{z}_j}{\sqrt{\sum_{i=1}^{m} \vert z_{ij} - \bar{z}_j \vert^{2}}\,}.\end{align*}
\begin{align*}x_{ij} = \frac{\tilde{z}_{ij}}{\sqrt{\sum_{i=1}^{m} \vert z_{ij} - \bar{z}_j \vert^{2}}\,} =\frac{z_{ij}-\bar{z}_j}{\sqrt{\sum_{i=1}^{m} \vert z_{ij} - \bar{z}_j \vert^{2}}\,}.\end{align*}
Thus, we could form the new
![]() $m \times n$
data matrix
$m \times n$
data matrix
![]() $\textbf X = (\textbf x_1,\ldots,\textbf x_n) \in \mathbb{C} ^{m \times n}$
(n samples and m features), where
$\textbf X = (\textbf x_1,\ldots,\textbf x_n) \in \mathbb{C} ^{m \times n}$
(n samples and m features), where
![]() $\textbf x_j = ( x_{1j}^{*},\ldots, x_{mj}^{*})^{*}$
. Finally, we focus on the self-normalized samples below. We shuffle each column of
$\textbf x_j = ( x_{1j}^{*},\ldots, x_{mj}^{*})^{*}$
. Finally, we focus on the self-normalized samples below. We shuffle each column of
![]() $\textbf X$
independently by randomly permuting its entries. Each column has a random permutation independent of all the other columns, and the permutation
$\textbf X$
independently by randomly permuting its entries. Each column has a random permutation independent of all the other columns, and the permutation
![]() $\boldsymbol{\pi}_j$
(
$\boldsymbol{\pi}_j$
(
![]() $j=1, \ldots, n$
) permutes the entries of the jth column of
$j=1, \ldots, n$
) permutes the entries of the jth column of
![]() $\textbf X $
, where
$\textbf X $
, where
![]() ${\pi}_1, \dots, {\pi}_n$
are n independent permutations of the set
${\pi}_1, \dots, {\pi}_n$
are n independent permutations of the set
![]() $ \{1, \ldots, m \} $
. Then, we obtain a permuted data matrix
$ \{1, \ldots, m \} $
. Then, we obtain a permuted data matrix
![]() $\textbf X_\pi$
, so
$\textbf X_\pi$
, so
![]() $\textbf X_\pi$
has entries
$\textbf X_\pi$
has entries
![]() ${({\textbf X_\pi})_{ij} = x_{\pi _i^{(j)},j}}$
,
${({\textbf X_\pi})_{ij} = x_{\pi _i^{(j)},j}}$
,
![]() $i=1, \ldots, m$
,
$i=1, \ldots, m$
,
![]() $j=1, \ldots, n$
. Let
$j=1, \ldots, n$
. Let
![]() ${\textbf x_{\pi^{(1)}}, \textbf x_{\pi^{(2)}}, \ldots, \textbf x_{\pi^{(n)}}}$
be the n columns of
${\textbf x_{\pi^{(1)}}, \textbf x_{\pi^{(2)}}, \ldots, \textbf x_{\pi^{(n)}}}$
be the n columns of
![]() $\textbf X_\pi$
. We propose a random permutation matrix model
$\textbf X_\pi$
. We propose a random permutation matrix model
where
![]() $\textbf{U}_n$
is a sequence of
$\textbf{U}_n$
is a sequence of
![]() $p \times m$
non-random complex matrices.
$p \times m$
non-random complex matrices.
In the literature, there are a few works on the eigenvalue distribution of random permutation matrices based on data permutation. The closest studies to this subject are the recent papers [Reference Hong, Sheng and Dobriban14, Reference Hu, Wang, Zhang and Zhou15], which prove that, with probability 1, the ESD of
![]() $({m}/{n})\textbf{N}_\pi\textbf{N}_\pi^\top$
for random permutation matrices
$({m}/{n})\textbf{N}_\pi\textbf{N}_\pi^\top$
for random permutation matrices
![]() $\textbf{N}_\pi$
weakly converges to the generalized Marčenko–Pastur distribution. Here,
$\textbf{N}_\pi$
weakly converges to the generalized Marčenko–Pastur distribution. Here,
![]() $\textbf N = \textbf{U} \textbf{X}$
,
$\textbf N = \textbf{U} \textbf{X}$
,
![]() $\textbf{U}$
is an
$\textbf{U}$
is an
![]() $m\times m$
diagonal matrix, and
$m\times m$
diagonal matrix, and
![]() $\textbf{N}_\pi$
is the randomly row-permuted matrix of
$\textbf{N}_\pi$
is the randomly row-permuted matrix of
![]() $\textbf N$
, i.e. for each
$\textbf N$
, i.e. for each
![]() $l \in \{1, \ldots, m\}$
, the entries of the lth row of
$l \in \{1, \ldots, m\}$
, the entries of the lth row of
![]() $\textbf{N}$
are randomly permuted. Compared to the results in [Reference Hong, Sheng and Dobriban14, Reference Hu, Wang, Zhang and Zhou15], we examine the LSD of a covariance matrix comprised of column-permuted data with a non-permuted matrix
$\textbf{N}$
are randomly permuted. Compared to the results in [Reference Hong, Sheng and Dobriban14, Reference Hu, Wang, Zhang and Zhou15], we examine the LSD of a covariance matrix comprised of column-permuted data with a non-permuted matrix
![]() $\textbf{U}_n$
. Moreover, we do not require
$\textbf{U}_n$
. Moreover, we do not require
![]() $\textbf{U}_n$
to be diagonal.
$\textbf{U}_n$
to be diagonal.
The approach used in this article is similar to that used by our third author in [Reference Bai and Zhou5], i.e. the Stieltjes transform
![]() $s_{F^{\textbf{B}_n}}(z)$
converges with probability 1 as
$s_{F^{\textbf{B}_n}}(z)$
converges with probability 1 as
![]() $n \to \infty $
to a limit, which can be divided into the following three key steps. We first apply the martingale technique to obtain almost sure convergence of the random part. Secondly, we select a deterministic matrix
$n \to \infty $
to a limit, which can be divided into the following three key steps. We first apply the martingale technique to obtain almost sure convergence of the random part. Secondly, we select a deterministic matrix
![]() $\textbf{K}$
to ensure the convergence of the non-random part. Finally, the existence and uniqueness of the solution of the system of equations (1) is established.
$\textbf{K}$
to ensure the convergence of the non-random part. Finally, the existence and uniqueness of the solution of the system of equations (1) is established.
Throughout the paper, let
![]() $\vert\textbf{A}\vert$
be the matrix whose (i, j)th entry is the absolute value of the (i, j)th entry of
$\vert\textbf{A}\vert$
be the matrix whose (i, j)th entry is the absolute value of the (i, j)th entry of
![]() $\textbf{A}$
. We denote the trace of a matrix
$\textbf{A}$
. We denote the trace of a matrix
![]() $\textbf{A}$
by
$\textbf{A}$
by
![]() $\operatorname{tr}(\textbf{A})$
. We denote the Hadamard product of two matrices
$\operatorname{tr}(\textbf{A})$
. We denote the Hadamard product of two matrices
![]() $\textbf{A}$
and
$\textbf{A}$
and
![]() $\textbf{C}$
of the same size by
$\textbf{C}$
of the same size by
![]() $\textbf{A} \circ \textbf{C}$
. For a
$\textbf{A} \circ \textbf{C}$
. For a
![]() $p\times n$
matrix
$p\times n$
matrix
![]() $\textbf{A}$
, the notation
$\textbf{A}$
, the notation
![]() $\|\textbf{A}\|$
means the spectral norm of the matrix
$\|\textbf{A}\|$
means the spectral norm of the matrix
![]() $\textbf{A}$
. The
$\textbf{A}$
. The
![]() $L_{p}$
norm of a vector
$L_{p}$
norm of a vector
![]() $ \textbf{x} \in \mathbb{R}^{m}$
is defined as
$ \textbf{x} \in \mathbb{R}^{m}$
is defined as
![]() $\|\textbf{x}\|_{p}=\big(\sum_{i=1}^{m} \vert x_{i}\vert^{p}\big)^{1 / p}$
,
$\|\textbf{x}\|_{p}=\big(\sum_{i=1}^{m} \vert x_{i}\vert^{p}\big)^{1 / p}$
,
![]() $p \geq 1$
. The symbol
$p \geq 1$
. The symbol
![]() $\stackrel{\text { a.s. }} {\longrightarrow}$
means almost sure convergence, and ‘
$\stackrel{\text { a.s. }} {\longrightarrow}$
means almost sure convergence, and ‘
![]() $*$
’ denotes the conventional conjugate transpose. We use big-O and little-o notation to express the asymptotic relationship between two quantities. And we also use L to denote various positive universal constants which may be different from one line to the next.
$*$
’ denotes the conventional conjugate transpose. We use big-O and little-o notation to express the asymptotic relationship between two quantities. And we also use L to denote various positive universal constants which may be different from one line to the next.
The remainder of the paper is structured as follows. In Section 2 we formulate the main result. In Section 3, application of this model is presented. Proofs of the main results are given in Section 4. Appendix A contains some auxiliary lemmas for convenience.
2. Main results
We begin to investigate the asymptotic properties of the ESD of random permutation matrices in high-dimensional frameworks, under the following assumptions.
Assumption 1.
![]() $c_n = p/n \to c \in (0, \infty)$
and
$c_n = p/n \to c \in (0, \infty)$
and
![]() $\gamma_n = m/n \to \gamma \in (0, \infty)$
as
$\gamma_n = m/n \to \gamma \in (0, \infty)$
as
![]() $n \to \infty$
.
$n \to \infty$
.
Assumption 2. Let
![]() $\textbf{U}_n$
be a sequence of
$\textbf{U}_n$
be a sequence of
![]() $p \times m$
non-random complex matrices. The spectral norm of the matrix
$p \times m$
non-random complex matrices. The spectral norm of the matrix
![]() $\textbf{T}_n = \textbf{U}_n \textbf{U}_n^{*}$
is uniformly bounded and its ESD converges weakly to a probability distribution H.
$\textbf{T}_n = \textbf{U}_n \textbf{U}_n^{*}$
is uniformly bounded and its ESD converges weakly to a probability distribution H.
Assumption 3. Let
![]() $\textbf X = (\textbf x_1, \ldots, \textbf x_n) \in \mathbb{C} ^{m \times n}$
be an
$\textbf X = (\textbf x_1, \ldots, \textbf x_n) \in \mathbb{C} ^{m \times n}$
be an
![]() $m \times n$
random matrix with, for all
$m \times n$
random matrix with, for all
![]() $j\in \{1, \ldots,n\}$
,
$j\in \{1, \ldots,n\}$
,
![]() $\sum_{i = 1}^m {x_{ij}} = 0$
,
$\sum_{i = 1}^m {x_{ij}} = 0$
,
![]() $\sum_{i = 1}^m {\vert x_{ij}\vert^2} = 1$
, and
$\sum_{i = 1}^m {\vert x_{ij}\vert^2} = 1$
, and
![]() $\sum_{i = 1}^m \mathbb{E}{\vert x_{ij}\vert^4} \to 0$
uniformly in
$\sum_{i = 1}^m \mathbb{E}{\vert x_{ij}\vert^4} \to 0$
uniformly in
![]() $j\le n$
, as
$j\le n$
, as
![]() $m \to \infty$
.
$m \to \infty$
.
The main result of this paper is as follows.
Theorem 1. Suppose that Assumptions 1–3 hold. Then, almost surely, the ESD of
![]() $\textbf{B}_n$
weakly converges to the generalized Marčenko–Pastur distribution, whose Stieltjes transform s(z) satisfies
$\textbf{B}_n$
weakly converges to the generalized Marčenko–Pastur distribution, whose Stieltjes transform s(z) satisfies
Remark 2. Note that in this theorem we do not need the entries of
![]() $\textbf X$
to be i.i.d. Moreover, the conditions
$\textbf X$
to be i.i.d. Moreover, the conditions
![]() $\sum_{i= 1}^m{x_{ij}} = 0$
and
$\sum_{i= 1}^m{x_{ij}} = 0$
and
![]() $\sum_{i= 1}^m\vert x_{ij}\vert^2 = 1$
hold after self-normalization and are necessary to make sure that the moment calculation is simpler under a very general dependence structure.
$\sum_{i= 1}^m\vert x_{ij}\vert^2 = 1$
hold after self-normalization and are necessary to make sure that the moment calculation is simpler under a very general dependence structure.
Remark 3. The condition
![]() $\sum_{i = 1}^m \mathbb{E} {\vert x_{ij}\vert^4 } \to 0$
is straightforward when the fourth moment of the raw data is finite uniformly, by the relationship between uniformly integrable and moment.
$\sum_{i = 1}^m \mathbb{E} {\vert x_{ij}\vert^4 } \to 0$
is straightforward when the fourth moment of the raw data is finite uniformly, by the relationship between uniformly integrable and moment.
Remark 4. When the entries
![]() $x_{ij}$
of
$x_{ij}$
of
![]() $\textbf X$
are non-random, we apply the same shuffling process to each column of
$\textbf X$
are non-random, we apply the same shuffling process to each column of
![]() $\textbf X$
. Theorem 1 apparently still holds.
$\textbf X$
. Theorem 1 apparently still holds.
Specifically, considering a non-random normalized vector
![]() $\textbf x = (x_1, x_2, \ldots, x_m)^{\top}$
, we permute the entries of
$\textbf x = (x_1, x_2, \ldots, x_m)^{\top}$
, we permute the entries of
![]() $\textbf x$
randomly n times to obtain random permutation matrices
$\textbf x$
randomly n times to obtain random permutation matrices
![]() $\textbf X_\pi$
. The permutation method is similar to sampling without replacement from finite populations. Thus, the following result is in line with Application 2.3 of the main theorem investigated by [Reference Bai and Zhou5].
$\textbf X_\pi$
. The permutation method is similar to sampling without replacement from finite populations. Thus, the following result is in line with Application 2.3 of the main theorem investigated by [Reference Bai and Zhou5].
Corollary 1. Let
![]() $\textbf X_\pi = (\textbf X_\pi)_{ij} \in \mathbb{R}^{m \times n}$
be a sequence of random permutation matrices with independent columns, where
$\textbf X_\pi = (\textbf X_\pi)_{ij} \in \mathbb{R}^{m \times n}$
be a sequence of random permutation matrices with independent columns, where
![]() $\textbf X_\pi$
is taken with respect to the non-random vector
$\textbf X_\pi$
is taken with respect to the non-random vector
![]() $\textbf x = (x_1, x_2, \ldots, x_m)^{\top}$
. Suppose that
$\textbf x = (x_1, x_2, \ldots, x_m)^{\top}$
. Suppose that
![]() $n, m \to \infty$
such that
$n, m \to \infty$
such that
![]() $\gamma_n = m/n \to \gamma > 0$
and the vector
$\gamma_n = m/n \to \gamma > 0$
and the vector
![]() $\textbf x$
satisfies
$\textbf x$
satisfies
![]() $\|\textbf{x}\|_2^{2} = 1$
,
$\|\textbf{x}\|_2^{2} = 1$
,
![]() $\|\textbf{x}\|_4^4 \to 0$
, and
$\|\textbf{x}\|_4^4 \to 0$
, and
![]() $\sum_{i = 1}^m{x_i} = 0$
. Then, with probability 1, the empirical spectral distribution of
$\sum_{i = 1}^m{x_i} = 0$
. Then, with probability 1, the empirical spectral distribution of
![]() $\textbf X_\pi\textbf X_\pi^{\top}$
converges weakly to the Marčenko–Pastur distribution, whose Stieltjes transform
$\textbf X_\pi\textbf X_\pi^{\top}$
converges weakly to the Marčenko–Pastur distribution, whose Stieltjes transform
![]() $s = s(z)$
satisfies
$s = s(z)$
satisfies
3. Application of the model
In this section, we discuss a potential application of the introduced model. Assume that
![]() ${W}_{1}, \ldots, {W}_{n} $
are n observations from the
${W}_{1}, \ldots, {W}_{n} $
are n observations from the
![]() $\operatorname{AR}(p)$
process defined as
$\operatorname{AR}(p)$
process defined as
![]() ${W}_{t}-{\phi}_{1} {W}_{t-1}-\cdots-{\phi}_{p} {W}_{t-p}={Z}_{t}$
, where
${W}_{t}-{\phi}_{1} {W}_{t-1}-\cdots-{\phi}_{p} {W}_{t-p}={Z}_{t}$
, where
![]() ${\phi}_{1}, \ldots, \phi_{p}$
are real constants,
${\phi}_{1}, \ldots, \phi_{p}$
are real constants,
![]() $(1-{\phi}_{1} z-\cdots-{\phi}_{p} z^{p}) \neq 0$
for
$(1-{\phi}_{1} z-\cdots-{\phi}_{p} z^{p}) \neq 0$
for
![]() $|z| \leqslant 1 $
, and
$|z| \leqslant 1 $
, and
![]() $ \{Z_{t}\} \stackrel{\mathrm{i.i.d.}}{\sim}(0, {\sigma}^2)$
, i.e.
$ \{Z_{t}\} \stackrel{\mathrm{i.i.d.}}{\sim}(0, {\sigma}^2)$
, i.e.
![]() $\{ Z_{t}\}$
are i.i.d. random variables with mean 0 and covariance
$\{ Z_{t}\}$
are i.i.d. random variables with mean 0 and covariance
![]() ${\sigma}^2>0$
. Recall that [Reference Chen, Davis and Brockwell8, Reference Chen, Davis, Brockwell and Bai9] advocated a selection algorithm by employing a data-driven penalty to select the proper model among AR(p). The algorithm is defined as follows. First, choose a fixed integer K, which is believed to be greater than the true order p, and compute the Yule–Walker estimates
${\sigma}^2>0$
. Recall that [Reference Chen, Davis and Brockwell8, Reference Chen, Davis, Brockwell and Bai9] advocated a selection algorithm by employing a data-driven penalty to select the proper model among AR(p). The algorithm is defined as follows. First, choose a fixed integer K, which is believed to be greater than the true order p, and compute the Yule–Walker estimates
![]() $\hat{{\phi}}_{K 1}, \ldots, \hat{{\phi}}_{K K}, \hat{{\sigma}}^2_{K}$
from the observed data,
$\hat{{\phi}}_{K 1}, \ldots, \hat{{\phi}}_{K K}, \hat{{\sigma}}^2_{K}$
from the observed data,
![]() $\{{W}_{t}\}_{t=1}^{n}$
. The residual sequence is given by
$\{{W}_{t}\}_{t=1}^{n}$
. The residual sequence is given by
![]() $\hat{{Z}}_{t}={W}_{t}-\hat{{\phi}}_{K 1}{W}_{t-1}-\cdots-\hat{{\phi}}_{K K} {W}_{t-K}$
for
$\hat{{Z}}_{t}={W}_{t}-\hat{{\phi}}_{K 1}{W}_{t-1}-\cdots-\hat{{\phi}}_{K K} {W}_{t-K}$
for
![]() $t=K+1, \ldots, n$
. Centralize and standardize the residuals by subtracting the sample mean
$t=K+1, \ldots, n$
. Centralize and standardize the residuals by subtracting the sample mean
![]() $\bar{{Z}}_{t}=1 / (n-K) \sum_{t=K+1}^{m} \widehat{{Z}}_{t}$
and standardized deviation
$\bar{{Z}}_{t}=1 / (n-K) \sum_{t=K+1}^{m} \widehat{{Z}}_{t}$
and standardized deviation
![]() $s_{nt}=\sqrt{1 / (n-K-1) \sum_{t=K+1}^{n} (\widehat{{Z}}_{t}-\bar{{Z}}_{t})^2}$
. For simplicity, we use the same notation
$s_{nt}=\sqrt{1 / (n-K-1) \sum_{t=K+1}^{n} (\widehat{{Z}}_{t}-\bar{{Z}}_{t})^2}$
. For simplicity, we use the same notation
![]() $\{\widehat{{Z}}_{t}\}_{K+1}^{n}$
for the normalized residuals. Then, choose a positive intege
$\{\widehat{{Z}}_{t}\}_{K+1}^{n}$
for the normalized residuals. Then, choose a positive intege
![]() $K_1 \leq K$
for each
$K_1 \leq K$
for each
![]() $k=0, \ldots, K_1$
, select proper
$k=0, \ldots, K_1$
, select proper
![]() $\operatorname{AR}$
coefficients
$\operatorname{AR}$
coefficients
![]() ${{\tilde\phi}}_{k 1}, \ldots, {{\tilde\phi}}_{k k}$
and construct a pseudo-
${{\tilde\phi}}_{k 1}, \ldots, {{\tilde\phi}}_{k k}$
and construct a pseudo-
![]() $\operatorname{AR}(k)$
series
$\operatorname{AR}(k)$
series
![]() ${Y}_{1}^{(k)}, \ldots, {Y}_{n}^{(k)}$
from the model
${Y}_{1}^{(k)}, \ldots, {Y}_{n}^{(k)}$
from the model
![]() ${Y}_{t}^{(k)}-{{\tilde\phi}}_{k 1} {Y}_{t-1}^{(k)}-\cdots-{{\tilde\phi}}_{k k} {Y}_{t-k}^{(k)}=\hat {Z}_{t}^{*}$
, where
${Y}_{t}^{(k)}-{{\tilde\phi}}_{k 1} {Y}_{t-1}^{(k)}-\cdots-{{\tilde\phi}}_{k k} {Y}_{t-k}^{(k)}=\hat {Z}_{t}^{*}$
, where
![]() $\{\hat {Z}_{t}^{*}\}$
is an i.i.d. sequence sampled from the normalized residuals,
$\{\hat {Z}_{t}^{*}\}$
is an i.i.d. sequence sampled from the normalized residuals,
![]() $\{\widehat{{Z}}_{t}\}_{K+1}^{n}$
. The case
$\{\widehat{{Z}}_{t}\}_{K+1}^{n}$
. The case
![]() $k=0$
corresponds to
$k=0$
corresponds to
![]() ${Y}_{t}^{(0)}=\hat {Z}_{t}^{*}$
. Note that
${Y}_{t}^{(0)}=\hat {Z}_{t}^{*}$
. Note that
![]() ${{\tilde\phi}}_{k 1}, \ldots, {{\tilde\phi}}_{k k}$
are user-selected coefficients in accordance with the real requirement of accuracy. Next, apply a larger set of pseudo-time series to approximate the range of correct penalty factors, and then ultimately make the estimated order of the model more accurate.
${{\tilde\phi}}_{k 1}, \ldots, {{\tilde\phi}}_{k k}$
are user-selected coefficients in accordance with the real requirement of accuracy. Next, apply a larger set of pseudo-time series to approximate the range of correct penalty factors, and then ultimately make the estimated order of the model more accurate.
In fact, the data-driven selection criterion can easily extend to the causal
![]() $\operatorname{ARMA}(p,q)$
process satisfying the recursive equation
$\operatorname{ARMA}(p,q)$
process satisfying the recursive equation
![]() ${\Phi}(B) {W}_{t}= {\Theta}(B) {Z}_{t}$
,
${\Phi}(B) {W}_{t}= {\Theta}(B) {Z}_{t}$
,
![]() $\{{Z}_{t}\} \sim {W N}(0, {\sigma^2})$
, where the polynomial
$\{{Z}_{t}\} \sim {W N}(0, {\sigma^2})$
, where the polynomial
![]() ${\Phi}(z)\;:\!=\;1 - {\phi}_{1} z-\cdots - {\phi}_{p} z^{p}$
satisfies the causality condition
${\Phi}(z)\;:\!=\;1 - {\phi}_{1} z-\cdots - {\phi}_{p} z^{p}$
satisfies the causality condition
![]() ${\Phi}(z) \neq 0$
for
${\Phi}(z) \neq 0$
for
![]() $|z| \leqslant 1 $
,
$|z| \leqslant 1 $
,
![]() ${\Theta}(z)\;:\!=\;1 + {\theta}_{1} z+\cdots+{\theta}_{q} z^{q}$
,
${\Theta}(z)\;:\!=\;1 + {\theta}_{1} z+\cdots+{\theta}_{q} z^{q}$
,
![]() ${W N}(0, {\sigma^2})$
stands for white noise with zero mean and variance
${W N}(0, {\sigma^2})$
stands for white noise with zero mean and variance
![]() $\sigma^2$
, and B as usual denotes the backward shift operator. By [Reference Brockwell and Davis6, Theorem 3.1.1 (Causality Criterion), p. 85], the causal
$\sigma^2$
, and B as usual denotes the backward shift operator. By [Reference Brockwell and Davis6, Theorem 3.1.1 (Causality Criterion), p. 85], the causal
![]() $\operatorname{ARMA}(p,q)$
process has the representation
$\operatorname{ARMA}(p,q)$
process has the representation
![]() ${W}_{t}={\Phi}^{-1}(B) {\Theta}(B) {Z}_{t}\;:\!=\; {\Psi}(B){Z}_{t}$
. Thus, we have the desired representation
${W}_{t}={\Phi}^{-1}(B) {\Theta}(B) {Z}_{t}\;:\!=\; {\Psi}(B){Z}_{t}$
. Thus, we have the desired representation
![]() $W_{t}=\sum_{i=0}^{\infty} \Psi_{i} Z_{t-i}$
, where the sequence
$W_{t}=\sum_{i=0}^{\infty} \Psi_{i} Z_{t-i}$
, where the sequence
![]() $\{\Psi_{i}\}$
is determined by
$\{\Psi_{i}\}$
is determined by
![]() $\Psi(z)=\sum_{i=0}^{\infty} \Psi_{i} z^{i}=\Theta(z) / \Phi(z)$
,
$\Psi(z)=\sum_{i=0}^{\infty} \Psi_{i} z^{i}=\Theta(z) / \Phi(z)$
,
![]() $|z| \leq 1$
.
$|z| \leq 1$
.
We deal with the causal
![]() $\operatorname{ARMA}(p,q)$
process similarly to the
$\operatorname{ARMA}(p,q)$
process similarly to the
![]() $\operatorname{AR}$
process. For the pair (K, Q), where it is believed that
$\operatorname{AR}$
process. For the pair (K, Q), where it is believed that
![]() $K\ge p$
and
$K\ge p$
and
![]() $Q\ge q$
, we could estimate the coefficients
$Q\ge q$
, we could estimate the coefficients
![]() $\hat\phi_k$
and
$\hat\phi_k$
and
![]() $\hat \theta_s$
from the observed data,
$\hat \theta_s$
from the observed data,
![]() $1 \le k\le K$
,
$1 \le k\le K$
,
![]() $1 \le s\le Q$
. Then, centralize and normalize the residuals after computing them using the estimated coefficients. Note that each column is a time series, so the coefficients are estimated by column, and thus the residuals are also calculated by column. Next, choose positive integers
$1 \le s\le Q$
. Then, centralize and normalize the residuals after computing them using the estimated coefficients. Note that each column is a time series, so the coefficients are estimated by column, and thus the residuals are also calculated by column. Next, choose positive integers
![]() $K_1 \leq K$
,
$K_1 \leq K$
,
![]() $Q_1 \leq Q$
, for each pair (k, s) and construct the pseudo-
$Q_1 \leq Q$
, for each pair (k, s) and construct the pseudo-
![]() $\operatorname{ARMA}(k,s)$
series
$\operatorname{ARMA}(k,s)$
series
![]() ${Y}_{j, t}^{(k,s)}$
for
${Y}_{j, t}^{(k,s)}$
for
![]() $k=1, \dots, K_1$
,
$k=1, \dots, K_1$
,
![]() $s=1, \ldots, Q_1$
from the model
$s=1, \ldots, Q_1$
from the model
where the coefficients
![]() $\tilde{{\Psi}}(B)$
are determined by the preselected coefficients of
$\tilde{{\Psi}}(B)$
are determined by the preselected coefficients of
![]() ${\Phi}(B)$
and
${\Phi}(B)$
and
![]() ${\Theta}(B)$
with the relation
${\Theta}(B)$
with the relation
![]() $\tilde{\Psi}(B)={\Phi}^{-1}(B) {\Theta}(B) $
, and set the residuals
$\tilde{\Psi}(B)={\Phi}^{-1}(B) {\Theta}(B) $
, and set the residuals
![]() $\{\hat {Z}_{t}^{*}\}$
to be sampled from the normalized residuals.
$\{\hat {Z}_{t}^{*}\}$
to be sampled from the normalized residuals.
![]() $\hat Z_{j,t}^{*}$
is assigned to be 0 if there is no such residual. Say, if the last coefficient is too small, the order of the model would be a lower one. Note that
$\hat Z_{j,t}^{*}$
is assigned to be 0 if there is no such residual. Say, if the last coefficient is too small, the order of the model would be a lower one. Note that
![]() $\hat{{\Psi}}(B)$
is an infinite series and there are only finitely many residuals, so one has to truncate the backward operator
$\hat{{\Psi}}(B)$
is an infinite series and there are only finitely many residuals, so one has to truncate the backward operator
![]() $\hat{{{\Psi}}}(B)$
to a finite sum, say the first m terms. In that way, the jth reconstructed series
$\hat{{{\Psi}}}(B)$
to a finite sum, say the first m terms. In that way, the jth reconstructed series
![]() $\textbf{Y}_{j}^{(k,s)} = ({Y}_{j,1}^{(k,s)}, \ldots, {Y}_{j,m}^{(k,s)} )^{\prime} $
in (4) can be written as
$\textbf{Y}_{j}^{(k,s)} = ({Y}_{j,1}^{(k,s)}, \ldots, {Y}_{j,m}^{(k,s)} )^{\prime} $
in (4) can be written as
where
 \begin{align*}\tilde{\boldsymbol{\Psi}} = \left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c}\tilde{{\Psi}}_{j,0} & 0 & 0 & \cdots & 0 \\[5pt] \tilde{{\Psi}}_{j,1} & \tilde{{\Psi}}_{j,0} & 0 & \ldots & 0 \\[5pt] \tilde{{\Psi}}_{j,2} & \tilde{{\Psi}}_{j,1} & \tilde{{\Psi}}_{j,0} & \cdots & 0\\[5pt] \vdots & \cdots & \cdots & \ddots & \vdots \\[5pt] \cdots &\cdots & \cdots & \cdots &\tilde{{\Psi}}_{j,0} \\[5pt] \end{array}\right).\end{align*}
\begin{align*}\tilde{\boldsymbol{\Psi}} = \left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c}\tilde{{\Psi}}_{j,0} & 0 & 0 & \cdots & 0 \\[5pt] \tilde{{\Psi}}_{j,1} & \tilde{{\Psi}}_{j,0} & 0 & \ldots & 0 \\[5pt] \tilde{{\Psi}}_{j,2} & \tilde{{\Psi}}_{j,1} & \tilde{{\Psi}}_{j,0} & \cdots & 0\\[5pt] \vdots & \cdots & \cdots & \ddots & \vdots \\[5pt] \cdots &\cdots & \cdots & \cdots &\tilde{{\Psi}}_{j,0} \\[5pt] \end{array}\right).\end{align*}
To avoid confusion, it is worth noting once more that the elements in the matrices
![]() $\tilde{\boldsymbol{\Psi}}$
are preselected here, similar to the way they were handled in [Reference Chen, Davis and Brockwell8, Reference Chen, Davis, Brockwell and Bai9]. Inspired by (5), the sample from the normalized residuals can also be regarded as a procedure for permuting the normalized residual sequences. Thus, the construction of pseudo-time series may benefit from a permutation of the normalized residuals to reduce sampling variability. This approach introduces increased randomness and enables the construction of a larger set of pseudo-series. This, in turn, provides a sound rationale for our proposed model (2). That is, the columns of
$\tilde{\boldsymbol{\Psi}}$
are preselected here, similar to the way they were handled in [Reference Chen, Davis and Brockwell8, Reference Chen, Davis, Brockwell and Bai9]. Inspired by (5), the sample from the normalized residuals can also be regarded as a procedure for permuting the normalized residual sequences. Thus, the construction of pseudo-time series may benefit from a permutation of the normalized residuals to reduce sampling variability. This approach introduces increased randomness and enables the construction of a larger set of pseudo-series. This, in turn, provides a sound rationale for our proposed model (2). That is, the columns of
![]() $\textbf X_n$
are permuted (corresponding to the permuted residuals), while those of
$\textbf X_n$
are permuted (corresponding to the permuted residuals), while those of
![]() $\textbf U_n$
(corresponding to the preselected coefficient matrices
$\textbf U_n$
(corresponding to the preselected coefficient matrices
![]() $\tilde{\boldsymbol{\Psi}}$
) remain as is.
$\tilde{\boldsymbol{\Psi}}$
) remain as is.
An attractive model order estimation technique was developed in [Reference Liang, Wilkes and Cadzow19, Reference Wax and Kailath27] based on the minimum eigenvalue of a covariance matrix derived from the observed data, which avoided the need for estimating the model parameters. In conjunction with the above discussion, we may make it feasible to estimate the true orders of the model by using the minimum eigenvalue of the covariance matrix of a larger set of pseudo-sequences. Consequently, the results established in this paper could offer useful insights for the theoretical analysis pertaining to data-driven model selection for order detection in time series. This prospect is indeed intriguing for future research. Nevertheless, the issue of model selection falls outside the scope of random matrix theory. For this reason, our discussion is limited to a straightforward description of the structure of the reconstructed models in this paper. The further investigation of the spectral properties of large-dimensional random permutation matrices in order determination for the causal
![]() $\operatorname{ARMA}(p,q)$
process will be left for future work.
$\operatorname{ARMA}(p,q)$
process will be left for future work.
4. Proof of the main result
Proof of Theorem 1. Throughout the proof, for any z we write
![]() $z=u+{\mathrm{i}} v$
, where u, v are the real and imaginary parts of z. Since
$z=u+{\mathrm{i}} v$
, where u, v are the real and imaginary parts of z. Since
![]() $z\in\mathbb C^+$
, we always have
$z\in\mathbb C^+$
, we always have
![]() $v>0$
. For convenience, in the following we write
$v>0$
. For convenience, in the following we write
 \begin{equation*} \textbf{B}_n \;:\!=\; \frac{m}{n}\textbf{U}_{n}\textbf{X}_\pi\textbf{X}_\pi^{*}\textbf{U}_{n}^{*} = \frac{m}{n}\sum_{k = 1}^n{\textbf{U}_{n}\textbf x_{\pi^{(k)}}\textbf x_{\pi^{(k)}}^{*}\textbf{U}_{n}^{*}}, \qquad \textbf{B}_{k,n} \;:\!=\; \Bigg(\sum_{k=1}^n{\textbf{r}_{k}\textbf{r}_{k}^{*}}\Bigg) - \textbf{r}_{k}\textbf{r}_{k}^{*}, \end{equation*}
\begin{equation*} \textbf{B}_n \;:\!=\; \frac{m}{n}\textbf{U}_{n}\textbf{X}_\pi\textbf{X}_\pi^{*}\textbf{U}_{n}^{*} = \frac{m}{n}\sum_{k = 1}^n{\textbf{U}_{n}\textbf x_{\pi^{(k)}}\textbf x_{\pi^{(k)}}^{*}\textbf{U}_{n}^{*}}, \qquad \textbf{B}_{k,n} \;:\!=\; \Bigg(\sum_{k=1}^n{\textbf{r}_{k}\textbf{r}_{k}^{*}}\Bigg) - \textbf{r}_{k}\textbf{r}_{k}^{*}, \end{equation*}
and
![]() $\textbf{r}_{k} = \sqrt{{m}/{n}}\textbf{U}_{n}\textbf x_{\pi^{(k)}}$
,
$\textbf{r}_{k} = \sqrt{{m}/{n}}\textbf{U}_{n}\textbf x_{\pi^{(k)}}$
,
![]() $k=1,\ldots,n$
. Note that the matrix
$k=1,\ldots,n$
. Note that the matrix
![]() $\textbf{B}_{k,n}$
is obtained from
$\textbf{B}_{k,n}$
is obtained from
![]() $\textbf {B}_n$
with
$\textbf {B}_n$
with
![]() $\textbf{r}_{k}$
removed. Recall that
$\textbf{r}_{k}$
removed. Recall that
![]() $s_{F^{\textbf{B}_n}}(z) = s_n(z) = p^{-1}\operatorname{tr}(({m}/{n})\textbf{U}_{n}\textbf{X}_\pi\textbf{X}_\pi^{*}\textbf{U}_{n}^{*}-z\textbf I_p)^{-1} = p^{-1}\operatorname{tr}\mathcal{B}_n^{-1}$
, where
$s_{F^{\textbf{B}_n}}(z) = s_n(z) = p^{-1}\operatorname{tr}(({m}/{n})\textbf{U}_{n}\textbf{X}_\pi\textbf{X}_\pi^{*}\textbf{U}_{n}^{*}-z\textbf I_p)^{-1} = p^{-1}\operatorname{tr}\mathcal{B}_n^{-1}$
, where
![]() $\mathcal B_n \;:\!=\; \textbf{B}_n - z\textbf I_p$
. We also write
$\mathcal B_n \;:\!=\; \textbf{B}_n - z\textbf I_p$
. We also write
![]() $\mathcal B_{k,n} \;:\!=\; \textbf{B}_{k,n} - z \textbf I_p$
. With this observation, we can make the following moment calculations:
$\mathcal B_{k,n} \;:\!=\; \textbf{B}_{k,n} - z \textbf I_p$
. With this observation, we can make the following moment calculations:
 \begin{align*} \mathbb Ex_{\pi _i^{(1)},j} & = \mathbb E\frac{{\sum_{i = 1}^m{x_{ij}}}}{m} = 0, \\[5pt] \mathbb E\vert x_{\pi_i^{(1)},j}\vert^2 & = \mathbb E\frac{{\sum_{i=1}^m{\vert x_{ij}\vert^2}}}{m} = \frac{1}{m}, \\[5pt] \mathbb Ex_{\pi_{i_1}^{(1)},j}\overline{x}_{\pi_{i_2}^{(1)},j} & = \mathbb E\frac{{\sum_{i_1 \ne i_2}^m{x_{i_1 j}}\overline{x}_{i_2 j}}}{{m({m - 1})}} = \frac{{-1}}{{m({m - 1})}}, \qquad i_1\neq i_2. \end{align*}
\begin{align*} \mathbb Ex_{\pi _i^{(1)},j} & = \mathbb E\frac{{\sum_{i = 1}^m{x_{ij}}}}{m} = 0, \\[5pt] \mathbb E\vert x_{\pi_i^{(1)},j}\vert^2 & = \mathbb E\frac{{\sum_{i=1}^m{\vert x_{ij}\vert^2}}}{m} = \frac{1}{m}, \\[5pt] \mathbb Ex_{\pi_{i_1}^{(1)},j}\overline{x}_{\pi_{i_2}^{(1)},j} & = \mathbb E\frac{{\sum_{i_1 \ne i_2}^m{x_{i_1 j}}\overline{x}_{i_2 j}}}{{m({m - 1})}} = \frac{{-1}}{{m({m - 1})}}, \qquad i_1\neq i_2. \end{align*}
We further write
![]() $\boldsymbol{\Sigma}_{\pi} \;:\!=\; \mathbb Ex_{\pi^{({{j}})}}x_{\pi^{({{j}})}}^{*}$
for
$\boldsymbol{\Sigma}_{\pi} \;:\!=\; \mathbb Ex_{\pi^{({{j}})}}x_{\pi^{({{j}})}}^{*}$
for
![]() $j=1, \ldots, n$
, which is in fact independent of j and will be denoted as
$j=1, \ldots, n$
, which is in fact independent of j and will be denoted as
![]() $\boldsymbol{\Sigma} _\pi = ({\sigma_{il}})$
for later use. Write
$\boldsymbol{\Sigma} _\pi = ({\sigma_{il}})$
for later use. Write
![]() $\boldsymbol{\widetilde\Sigma}_\pi = \textbf I_m - ({1}/{m})\textbf{1}\textbf{1}^{*}$
, which is in fact
$\boldsymbol{\widetilde\Sigma}_\pi = \textbf I_m - ({1}/{m})\textbf{1}\textbf{1}^{*}$
, which is in fact
![]() $(m-1)\boldsymbol{\Sigma}_{\pi}$
, i.e.
$(m-1)\boldsymbol{\Sigma}_{\pi}$
, i.e.
![]() $\boldsymbol{\Sigma}_{\pi} = ({1}/({m-1}))\boldsymbol{\widetilde\Sigma}_\pi$
, and
$\boldsymbol{\Sigma}_{\pi} = ({1}/({m-1}))\boldsymbol{\widetilde\Sigma}_\pi$
, and
![]() $\textbf{1} = (1,\ldots,1)^{*}$
.
$\textbf{1} = (1,\ldots,1)^{*}$
.
According to [Reference Bai and Silverstein3, Theorem B.9], the almost sure convergence of the Stieltjes transform
![]() $s_n(z)$
to s(z) ensures that the ESD weakly converges to a probability distribution almost surely. Thus, we proceed with the proof by the following two steps:
$s_n(z)$
to s(z) ensures that the ESD weakly converges to a probability distribution almost surely. Thus, we proceed with the proof by the following two steps:
-
(i)
 $s_n(z) - \mathbb E s_n(z) \stackrel{\text{a.s.}}{\longrightarrow}0$
;
$s_n(z) - \mathbb E s_n(z) \stackrel{\text{a.s.}}{\longrightarrow}0$
; -
(ii)
 $\mathbb E s_n(z) \to s(z)$
, which satisfies (3).
$\mathbb E s_n(z) \to s(z)$
, which satisfies (3).
Step (i):
![]() $s_n(z) - \mathbb{E} s_n(z) \stackrel{\text { a.s. }}{\longrightarrow} 0$
. Let
$s_n(z) - \mathbb{E} s_n(z) \stackrel{\text { a.s. }}{\longrightarrow} 0$
. Let
![]() $\mathbb E_k(\cdot) = \mathbb E(\,\cdot\mid\textbf x_{\pi^{({{{k+1}}})}},\ldots,\textbf x_{\pi^{(n)}})$
denote the conditional expectation with respect to the
$\mathbb E_k(\cdot) = \mathbb E(\,\cdot\mid\textbf x_{\pi^{({{{k+1}}})}},\ldots,\textbf x_{\pi^{(n)}})$
denote the conditional expectation with respect to the
![]() $\sigma$
-field generated by
$\sigma$
-field generated by
![]() $\textbf x_{\pi^{({{{k+1}}})}},\ldots,\textbf x_{\pi^{(n)}}$
. It follows that
$\textbf x_{\pi^{({{{k+1}}})}},\ldots,\textbf x_{\pi^{(n)}}$
. It follows that
![]() $\mathbb Es_n(z) = \mathbb E_n({s_n(z)})$
and
$\mathbb Es_n(z) = \mathbb E_n({s_n(z)})$
and
![]() $s_n(z) = \mathbb E_0({s_n(z)})$
. Similar to [Reference Bai2], we can write
$s_n(z) = \mathbb E_0({s_n(z)})$
. Similar to [Reference Bai2], we can write
![]() $s_n(z) - \mathbb{E}s_n(z)$
as the sum of martingale differences, i.e.
$s_n(z) - \mathbb{E}s_n(z)$
as the sum of martingale differences, i.e.
 \begin{align*} s_n(z) - \mathbb{E} s_n(z) & = \mathbb{E}_0 s_n(z) - \mathbb{E}_n s_n(z) \\[5pt] & = \sum_{k=1}^n (\mathbb{E}_{k-1} s_n(z) - \mathbb{E}_k s_n(z)) \\[5pt] & = \frac{1}{p}\sum_{k=1}^n(\mathbb{E}_{k-1}-\mathbb{E}_k) \big(\mathrm{tr}\,\mathcal{B}_n^{-1} - \operatorname{tr}\mathcal{B}_{k,n}^{-1}\big) = \frac{1}{p}\sum_{k=1}^n(\mathbb{E}_{k-1}-\mathbb{E}_k)\varepsilon_k, \end{align*}
\begin{align*} s_n(z) - \mathbb{E} s_n(z) & = \mathbb{E}_0 s_n(z) - \mathbb{E}_n s_n(z) \\[5pt] & = \sum_{k=1}^n (\mathbb{E}_{k-1} s_n(z) - \mathbb{E}_k s_n(z)) \\[5pt] & = \frac{1}{p}\sum_{k=1}^n(\mathbb{E}_{k-1}-\mathbb{E}_k) \big(\mathrm{tr}\,\mathcal{B}_n^{-1} - \operatorname{tr}\mathcal{B}_{k,n}^{-1}\big) = \frac{1}{p}\sum_{k=1}^n(\mathbb{E}_{k-1}-\mathbb{E}_k)\varepsilon_k, \end{align*}
where
![]() $\varepsilon_k \;:\!=\; \operatorname{tr}\mathcal{B}_n^{-1} - \operatorname{tr}\mathcal{B}_{k,n}^{-1}$
. Notice that
$\varepsilon_k \;:\!=\; \operatorname{tr}\mathcal{B}_n^{-1} - \operatorname{tr}\mathcal{B}_{k,n}^{-1}$
. Notice that
 \begin{align*} \mathcal{B}_{n}^{-1} = \mathcal{B}_{k,n}^{-1} - \frac{\mathcal{B}_{k,n}^{-1}(\textbf{r}_{k}\textbf{r}_{k}^{*})\mathcal{B}_{k,n}^{-1}} {1 + \textbf{r}_{k}^{*}\mathcal{B}_{k,n}^{-1}\textbf{r}_{k}}. \end{align*}
\begin{align*} \mathcal{B}_{n}^{-1} = \mathcal{B}_{k,n}^{-1} - \frac{\mathcal{B}_{k,n}^{-1}(\textbf{r}_{k}\textbf{r}_{k}^{*})\mathcal{B}_{k,n}^{-1}} {1 + \textbf{r}_{k}^{*}\mathcal{B}_{k,n}^{-1}\textbf{r}_{k}}. \end{align*}
By Lemma 1, we have
 \begin{align*} \vert\varepsilon_k\vert \le \frac{\|\mathcal{B}_{k,n}^{-1}\textbf{r}_{k}\|^2} {\vert 1 + \textbf{r}_{k}^{*}\mathcal{B}_{k,n}^{-1}\textbf{r}_{k}\vert} \leq v^{-1}. \end{align*}
\begin{align*} \vert\varepsilon_k\vert \le \frac{\|\mathcal{B}_{k,n}^{-1}\textbf{r}_{k}\|^2} {\vert 1 + \textbf{r}_{k}^{*}\mathcal{B}_{k,n}^{-1}\textbf{r}_{k}\vert} \leq v^{-1}. \end{align*}
It follows that
![]() $(\mathbb{E}_{k-1}-\mathbb{E}_k)\varepsilon_k$
forms a bounded martingale difference sequence. By the Burkholder inequality (see Lemma 2), this yields
$(\mathbb{E}_{k-1}-\mathbb{E}_k)\varepsilon_k$
forms a bounded martingale difference sequence. By the Burkholder inequality (see Lemma 2), this yields
 \begin{equation*} \mathbb{E}\vert s_n(z) - \mathbb{E} s_n(z)\vert^q \leq K_q p^{-q}\mathbb{E}\Bigg(\sum_{k=1}^n\vert(\mathbb{E}_{k-1}-\mathbb{E}_k)\gamma_k\vert^2\Bigg)^{q/2} \leq K_q\bigg(\frac{2}{v}\bigg)^q p^{-q/2}\bigg(\frac{p}{n}\bigg)^{-q/2}, \end{equation*}
\begin{equation*} \mathbb{E}\vert s_n(z) - \mathbb{E} s_n(z)\vert^q \leq K_q p^{-q}\mathbb{E}\Bigg(\sum_{k=1}^n\vert(\mathbb{E}_{k-1}-\mathbb{E}_k)\gamma_k\vert^2\Bigg)^{q/2} \leq K_q\bigg(\frac{2}{v}\bigg)^q p^{-q/2}\bigg(\frac{p}{n}\bigg)^{-q/2}, \end{equation*}
which implies that it is summable for
![]() $q > 2$
. By the Borel–Cantelli lemma,
$q > 2$
. By the Borel–Cantelli lemma,
![]() $s_n(z) - \mathbb{E}s_n(z) = p^{-1}\sum_{k=1}^n(\mathbb{E}_{k-1} - \mathbb{E}_k)\varepsilon_k \stackrel{\text{a.s.}}{\longrightarrow} 0$
is obtained.
$s_n(z) - \mathbb{E}s_n(z) = p^{-1}\sum_{k=1}^n(\mathbb{E}_{k-1} - \mathbb{E}_k)\varepsilon_k \stackrel{\text{a.s.}}{\longrightarrow} 0$
is obtained.
Step (ii):
![]() $\mathbb{E} s_n(z) \to s(z)$
. The fundamental technique of the approach is to surmise the deterministic equivalent of
$\mathbb{E} s_n(z) \to s(z)$
. The fundamental technique of the approach is to surmise the deterministic equivalent of
![]() $s_n(z)$
by writing it in the form
$s_n(z)$
by writing it in the form
![]() $p^{-1}\operatorname{tr}(\textbf K - z\textbf{I}_p)^{-1}$
at first, where
$p^{-1}\operatorname{tr}(\textbf K - z\textbf{I}_p)^{-1}$
at first, where
![]() $\textbf K$
is assumed to be deterministic. Then, it will be performed by taking the difference
$\textbf K$
is assumed to be deterministic. Then, it will be performed by taking the difference
![]() $p^{-1}\mathbb E\operatorname{tr}(\textbf{B}_n - z\textbf{I}_p)^{-1} - p^{-1}\mathbb E\operatorname{tr}(\textbf K - z\textbf{I}_p)^{-1}$
and, during the calculation, determining
$p^{-1}\mathbb E\operatorname{tr}(\textbf{B}_n - z\textbf{I}_p)^{-1} - p^{-1}\mathbb E\operatorname{tr}(\textbf K - z\textbf{I}_p)^{-1}$
and, during the calculation, determining
![]() $\textbf K$
such that the difference tends to zero. Define
$\textbf K$
such that the difference tends to zero. Define
Since
 \begin{equation*} (\textbf{B}_n - z \textbf I_p) - (\textbf K - z \textbf I_p) = \Bigg\{{\sum\limits_{i=1}^n{\textbf{r}_{k}\textbf{r}_{k}^{*}}}\Bigg\} - \textbf K , \end{equation*}
\begin{equation*} (\textbf{B}_n - z \textbf I_p) - (\textbf K - z \textbf I_p) = \Bigg\{{\sum\limits_{i=1}^n{\textbf{r}_{k}\textbf{r}_{k}^{*}}}\Bigg\} - \textbf K , \end{equation*}
by (20) of Lemma 3 and the resolvent identity
![]() $\textbf{A}^{-1} - \textbf{C}^{-1} = -\textbf{A}^{-1}(\textbf{A}-\textbf{C})\textbf{C}^{-1}$
for any
$\textbf{A}^{-1} - \textbf{C}^{-1} = -\textbf{A}^{-1}(\textbf{A}-\textbf{C})\textbf{C}^{-1}$
for any
![]() $p \times p$
invertible matrices
$p \times p$
invertible matrices
![]() $\textbf A$
and
$\textbf A$
and
![]() $\textbf C$
, we have
$\textbf C$
, we have
 \begin{align} & (\textbf K-z\textbf I_p)^{-1} - (\textbf{B}_n - z\textbf I_p)^{-1} \nonumber\\ & \quad = (\textbf K-z\textbf I_p)^{-1}((\textbf{B}_n - z\textbf I_p) - (\textbf K-z\textbf I_p)) (\textbf{B}_n - z\textbf I_p)^{-1} \nonumber \\[5pt] & \quad = \Bigg\{\sum_{k=1}^n(\textbf K - z\textbf I_p)^{-1}\textbf{r}_{k}\textbf{r}_{k}^{*} (\textbf{B}_n - z\textbf I_p)^{-1}\Bigg\} - (\textbf K - z\textbf I_p)^{-1}\textbf K(\textbf{B}_n - z\textbf I_p)^{-1} \nonumber \\[5pt] & \quad = \Bigg\{\sum_{k=1}^n\frac{(\textbf K - z\textbf I_p)^{-1}(\textbf{r}_{k}\textbf{r}_{k}^{*})\mathcal{B}_{k,n}^{-1}} {1 + \textbf{r}_{k}^{*}\mathcal{B}_{k,n}^{-1}\textbf{r}_{k}}\Bigg\} - (\textbf K - z\textbf I_p)^{-1}\textbf K(\textbf{B}_n - z\textbf I_p)^{-1}. \end{align}
\begin{align} & (\textbf K-z\textbf I_p)^{-1} - (\textbf{B}_n - z\textbf I_p)^{-1} \nonumber\\ & \quad = (\textbf K-z\textbf I_p)^{-1}((\textbf{B}_n - z\textbf I_p) - (\textbf K-z\textbf I_p)) (\textbf{B}_n - z\textbf I_p)^{-1} \nonumber \\[5pt] & \quad = \Bigg\{\sum_{k=1}^n(\textbf K - z\textbf I_p)^{-1}\textbf{r}_{k}\textbf{r}_{k}^{*} (\textbf{B}_n - z\textbf I_p)^{-1}\Bigg\} - (\textbf K - z\textbf I_p)^{-1}\textbf K(\textbf{B}_n - z\textbf I_p)^{-1} \nonumber \\[5pt] & \quad = \Bigg\{\sum_{k=1}^n\frac{(\textbf K - z\textbf I_p)^{-1}(\textbf{r}_{k}\textbf{r}_{k}^{*})\mathcal{B}_{k,n}^{-1}} {1 + \textbf{r}_{k}^{*}\mathcal{B}_{k,n}^{-1}\textbf{r}_{k}}\Bigg\} - (\textbf K - z\textbf I_p)^{-1}\textbf K(\textbf{B}_n - z\textbf I_p)^{-1}. \end{align}
Let
![]() $\textbf T_n^0=\textbf I_p$
and
$\textbf T_n^0=\textbf I_p$
and
![]() $\textbf T_n^1=\textbf T_n$
. Multiplying
$\textbf T_n^1=\textbf T_n$
. Multiplying
![]() $({1}/{p})\textbf T_n^{l}$
for
$({1}/{p})\textbf T_n^{l}$
for
![]() $l=0, 1$
on both sides of (6), and then taking the trace and expectation, we obtain that
$l=0, 1$
on both sides of (6), and then taking the trace and expectation, we obtain that
 \begin{multline} \frac{1}{p}\mathbb E\operatorname{tr}\textbf T_n^{l}(\textbf K-z\textbf I_p)^{-1} - \frac{1}{p}\mathbb E\operatorname{tr}\textbf T_n^{l}(\textbf{B}_n - z\textbf I_p)^{-1} \\[5pt] = \frac{1}{p}\mathbb E\Bigg\{\sum_{k=1}^n \frac{\textbf{r}_{k}^{*}\mathcal{B}_{k,n}^{-1}\textbf T_n^{l}(\textbf K - z\textbf I_p)^{-1}\textbf{r}_{k}} {1 + \textbf{r}_{k}^{*}\mathcal{B}_{k,n}^{-1}\textbf{r}_{k}}\Bigg\} - \frac{1}{p}\mathbb E\operatorname{tr}\textbf T^{l}_n(\textbf K - z\textbf I_p)^{-1}\textbf K (\textbf{B}_n - z\textbf I_p)^{-1} . \end{multline}
\begin{multline} \frac{1}{p}\mathbb E\operatorname{tr}\textbf T_n^{l}(\textbf K-z\textbf I_p)^{-1} - \frac{1}{p}\mathbb E\operatorname{tr}\textbf T_n^{l}(\textbf{B}_n - z\textbf I_p)^{-1} \\[5pt] = \frac{1}{p}\mathbb E\Bigg\{\sum_{k=1}^n \frac{\textbf{r}_{k}^{*}\mathcal{B}_{k,n}^{-1}\textbf T_n^{l}(\textbf K - z\textbf I_p)^{-1}\textbf{r}_{k}} {1 + \textbf{r}_{k}^{*}\mathcal{B}_{k,n}^{-1}\textbf{r}_{k}}\Bigg\} - \frac{1}{p}\mathbb E\operatorname{tr}\textbf T^{l}_n(\textbf K - z\textbf I_p)^{-1}\textbf K (\textbf{B}_n - z\textbf I_p)^{-1} . \end{multline}
Note that
 \begin{align} \mathbb E\bigg\vert\big(1 + \textbf{r}_{k}^{*}\mathcal{B}_{k,n}^{-1}\textbf{r}_{k}\big) - \bigg(1 & + \frac{m}{n}\mathbb E\operatorname{tr}\textbf U_n^{*} \mathcal{B}_{n}^{-1}\textbf U_n\boldsymbol{\Sigma}_\pi\bigg)\bigg\vert^2 \nonumber \\[5pt] & \leq \mathbb E\bigg\vert\textbf{r}_{k}^{*}\mathcal{B}_{k,n}^{-1}\textbf{r}_{k} - \frac{m}{n}\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{k,n}^{-1}\textbf U_n\boldsymbol{\Sigma}_\pi \notag \\[5pt] & \qquad + \frac{m}{n}\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{k,n}^{-1}\textbf U_n\boldsymbol{\Sigma}_\pi - \frac{m}{n}\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1}\textbf U_n\boldsymbol{\Sigma}_\pi \notag \\[5pt] & \qquad + \frac{m}{n}\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1}\textbf U_n\boldsymbol{\Sigma}_\pi - \frac{m}{n}\mathbb E\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1}\textbf U_n \boldsymbol{\Sigma}_\pi\bigg\vert^2 \notag \\[5pt] & \leq 3\gamma\bigg(\mathbb E\big\vert\textbf x_{\pi^{(k)}}^{*}\textbf{U}_{n}^{*}\mathcal{B}_{k,n}^{-1} \textbf{U}_{n}\textbf x_{\pi^{(k)}} - \operatorname{tr}\textbf U_n^{*}\mathcal{B}_{k,n}^{-1}\textbf U_n\boldsymbol{\Sigma}_\pi\big\vert^2 \end{align}
\begin{align} \mathbb E\bigg\vert\big(1 + \textbf{r}_{k}^{*}\mathcal{B}_{k,n}^{-1}\textbf{r}_{k}\big) - \bigg(1 & + \frac{m}{n}\mathbb E\operatorname{tr}\textbf U_n^{*} \mathcal{B}_{n}^{-1}\textbf U_n\boldsymbol{\Sigma}_\pi\bigg)\bigg\vert^2 \nonumber \\[5pt] & \leq \mathbb E\bigg\vert\textbf{r}_{k}^{*}\mathcal{B}_{k,n}^{-1}\textbf{r}_{k} - \frac{m}{n}\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{k,n}^{-1}\textbf U_n\boldsymbol{\Sigma}_\pi \notag \\[5pt] & \qquad + \frac{m}{n}\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{k,n}^{-1}\textbf U_n\boldsymbol{\Sigma}_\pi - \frac{m}{n}\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1}\textbf U_n\boldsymbol{\Sigma}_\pi \notag \\[5pt] & \qquad + \frac{m}{n}\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1}\textbf U_n\boldsymbol{\Sigma}_\pi - \frac{m}{n}\mathbb E\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1}\textbf U_n \boldsymbol{\Sigma}_\pi\bigg\vert^2 \notag \\[5pt] & \leq 3\gamma\bigg(\mathbb E\big\vert\textbf x_{\pi^{(k)}}^{*}\textbf{U}_{n}^{*}\mathcal{B}_{k,n}^{-1} \textbf{U}_{n}\textbf x_{\pi^{(k)}} - \operatorname{tr}\textbf U_n^{*}\mathcal{B}_{k,n}^{-1}\textbf U_n\boldsymbol{\Sigma}_\pi\big\vert^2 \end{align}
where the last inequality follows from Jensen’s inequality. For (8), writing
![]() $\textbf{B}=\textbf U_n^{*}\mathcal B_{k,n}^{-1}\textbf U_n = (b_{il})$
and
$\textbf{B}=\textbf U_n^{*}\mathcal B_{k,n}^{-1}\textbf U_n = (b_{il})$
and
![]() $\boldsymbol{\Sigma}_\pi = ({\sigma_{il}})$
, we can obtain that
$\boldsymbol{\Sigma}_\pi = ({\sigma_{il}})$
, we can obtain that
 \begin{align} \mathbb E\big\vert{\textbf x_{\pi^{(k)}}^{*}\textbf{U}_{n}^{*}\mathcal{B}_{k,n}^{-1} \textbf{U}_{n}\textbf x_{\pi^{(k)}}} - \operatorname{tr}\textbf U_n^{*}\mathcal{B}_{k,n}^{-1}\textbf U_n\boldsymbol{\Sigma}_\pi\big\vert^2 = \mathbb E\Bigg\vert{\sum_{i=1}^m{\sum_{l=1}^m{b_{il}}}\big({x_{\pi_i^{(k)},k}x_{\pi_l^{(k)},k}-\sigma_{il}}\big)} \Bigg\vert^2 \to 0. \end{align}
\begin{align} \mathbb E\big\vert{\textbf x_{\pi^{(k)}}^{*}\textbf{U}_{n}^{*}\mathcal{B}_{k,n}^{-1} \textbf{U}_{n}\textbf x_{\pi^{(k)}}} - \operatorname{tr}\textbf U_n^{*}\mathcal{B}_{k,n}^{-1}\textbf U_n\boldsymbol{\Sigma}_\pi\big\vert^2 = \mathbb E\Bigg\vert{\sum_{i=1}^m{\sum_{l=1}^m{b_{il}}}\big({x_{\pi_i^{(k)},k}x_{\pi_l^{(k)},k}-\sigma_{il}}\big)} \Bigg\vert^2 \to 0. \end{align}
Since the calculation of (11) is tedious, we postpone it to the appendix for interested readers. For (9), it follows from Lemma 1 that, as
![]() $m \to \infty$
,
$m \to \infty$
,
which implies that (9) converges to zero. For (10), by the similar martingale decomposition in Step (i) and Lemma 2, we have, as
![]() $n \to \infty$
,
$n \to \infty$
,
 \begin{align*} &\mathbb E\bigg\vert\frac{1}{m-1}\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1} \textbf U_n\boldsymbol{\widetilde\Sigma}_\pi - \frac{1}{m-1}\mathbb E\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1} \textbf U_n\boldsymbol{\widetilde\Sigma}_\pi\bigg\vert^2 \\[9pt] & \quad \leq K_2(m-1)^{-2}\mathbb E\Bigg(\sum_{k=1}^n\big\vert(\mathbb E_{k-1}-\mathbb E_k) (\operatorname{tr}\textbf U_n^{*}\boldsymbol{\widetilde\Sigma}_\pi\textbf U_n\mathcal{B}_{n}^{-1} - \operatorname{tr}\textbf U_n^{*}\boldsymbol{\widetilde\Sigma}_\pi\textbf U_n\mathcal{B}_{k,n}^{-1}) \big\vert^2\Bigg) \\[9pt] & \quad \leq K_2\Bigg(\frac{2\big\|\textbf U_n^{*}\boldsymbol{\widetilde\Sigma}_\pi\textbf U_n\big\|}{v}\Bigg)^2 (m-1)^{-1}\bigg(\frac{m-1}{n}\bigg)^{-1} \to 0. \end{align*}
\begin{align*} &\mathbb E\bigg\vert\frac{1}{m-1}\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1} \textbf U_n\boldsymbol{\widetilde\Sigma}_\pi - \frac{1}{m-1}\mathbb E\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1} \textbf U_n\boldsymbol{\widetilde\Sigma}_\pi\bigg\vert^2 \\[9pt] & \quad \leq K_2(m-1)^{-2}\mathbb E\Bigg(\sum_{k=1}^n\big\vert(\mathbb E_{k-1}-\mathbb E_k) (\operatorname{tr}\textbf U_n^{*}\boldsymbol{\widetilde\Sigma}_\pi\textbf U_n\mathcal{B}_{n}^{-1} - \operatorname{tr}\textbf U_n^{*}\boldsymbol{\widetilde\Sigma}_\pi\textbf U_n\mathcal{B}_{k,n}^{-1}) \big\vert^2\Bigg) \\[9pt] & \quad \leq K_2\Bigg(\frac{2\big\|\textbf U_n^{*}\boldsymbol{\widetilde\Sigma}_\pi\textbf U_n\big\|}{v}\Bigg)^2 (m-1)^{-1}\bigg(\frac{m-1}{n}\bigg)^{-1} \to 0. \end{align*}
Therefore, by combining (8), (9), and (10), we obtain
Moreover, note that
It then follows from (7) and (12) that
 \begin{align*} \frac{1}{p}\mathbb E\Bigg\{\sum_{k=1}^n & \frac{\textbf{r}_{k}^{*}\mathcal{B}_{k,n}^{-1}\textbf T_n^{l}(\textbf K - z\textbf I_p)^{-1}\textbf{r}_{k}} {1 + \textbf{r}_{k}^{*}\mathcal{B}_{k,n}^{-1}\textbf{r}_{k}}\Bigg\} - \frac{1}{p}\mathbb E\operatorname{tr}\textbf T^{l}_n(\textbf K - z\textbf I_p)^{-1}\textbf K (\textbf{B}_n - z\textbf I_p)^{-1} \\[5pt] & = \frac{1}{p}\sum_{k=1}^n\mathbb E\bigg\{ \textbf{r}_{k}^{*}\mathcal{B}_{k,n}^{-1}\textbf T_n^{l}(\textbf K - z\textbf I_p)^{-1} \textbf{r}_{k}\bigg(1 + \frac{m}{n}\mathbb E\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1} \textbf U_n\boldsymbol{\Sigma}_\pi\bigg)^{-1}\bigg\} \\[5pt] & \quad - \frac{1}{p}\mathbb E\operatorname{tr}\mathcal B_{n}^{-1}\textbf T^{l}_n(\textbf K - z\textbf I_p)^{-1} \textbf K + o(1) \\[5pt] & = \frac{1}{np}\sum_{k=1}^n\mathbb E\bigg\{\operatorname{tr}\mathcal B_{k,n}^{-1}\textbf T_n^{l} (\textbf K - z\textbf I_p)^{-1}\textbf{U}_n\boldsymbol{\widetilde\Sigma}_\pi\textbf U_n^{*} \bigg(1 + \frac{m}{n}\mathbb E\operatorname{tr}\mathcal{B}_{n}^{-1}\textbf U_n\boldsymbol{\Sigma}_\pi \textbf U_n^{*}\bigg)^{-1}\bigg\} \\[5pt] & \quad - \frac{1}{p}\mathbb E\operatorname{tr}\mathcal B_{n}^{-1}\textbf T^{l}_n(\textbf K - z\textbf I_p)^{-1} \textbf K + o(1) \\[5pt] & = \frac{1}{np}\sum_{k=1}^n\mathbb E \big\{\operatorname{tr}\mathcal B_{k,n}^{-1}\textbf T_n^{l}(\textbf K - z\textbf I_p)^{-1}\textbf K\big\} - \frac{1}{p}\mathbb E\operatorname{tr}\mathcal B_{n}^{-1}\textbf T^{l}_n(\textbf K - z\textbf I_p)^{-1} \textbf K + o(1) \\[5pt] & = \frac{1}{np}\sum_{k=1}^n\big\{\mathbb E\operatorname{tr}\mathcal B_{k,n}^{-1}\textbf T_n^{l} (\textbf K - z\textbf I_p)^{-1}\textbf K - \mathbb E\operatorname{tr}\mathcal B_{n}^{-1}\textbf T^{l}_n(\textbf K - z\textbf I_p)^{-1} \textbf K\big\} + o(1) = o(1), \end{align*}
\begin{align*} \frac{1}{p}\mathbb E\Bigg\{\sum_{k=1}^n & \frac{\textbf{r}_{k}^{*}\mathcal{B}_{k,n}^{-1}\textbf T_n^{l}(\textbf K - z\textbf I_p)^{-1}\textbf{r}_{k}} {1 + \textbf{r}_{k}^{*}\mathcal{B}_{k,n}^{-1}\textbf{r}_{k}}\Bigg\} - \frac{1}{p}\mathbb E\operatorname{tr}\textbf T^{l}_n(\textbf K - z\textbf I_p)^{-1}\textbf K (\textbf{B}_n - z\textbf I_p)^{-1} \\[5pt] & = \frac{1}{p}\sum_{k=1}^n\mathbb E\bigg\{ \textbf{r}_{k}^{*}\mathcal{B}_{k,n}^{-1}\textbf T_n^{l}(\textbf K - z\textbf I_p)^{-1} \textbf{r}_{k}\bigg(1 + \frac{m}{n}\mathbb E\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1} \textbf U_n\boldsymbol{\Sigma}_\pi\bigg)^{-1}\bigg\} \\[5pt] & \quad - \frac{1}{p}\mathbb E\operatorname{tr}\mathcal B_{n}^{-1}\textbf T^{l}_n(\textbf K - z\textbf I_p)^{-1} \textbf K + o(1) \\[5pt] & = \frac{1}{np}\sum_{k=1}^n\mathbb E\bigg\{\operatorname{tr}\mathcal B_{k,n}^{-1}\textbf T_n^{l} (\textbf K - z\textbf I_p)^{-1}\textbf{U}_n\boldsymbol{\widetilde\Sigma}_\pi\textbf U_n^{*} \bigg(1 + \frac{m}{n}\mathbb E\operatorname{tr}\mathcal{B}_{n}^{-1}\textbf U_n\boldsymbol{\Sigma}_\pi \textbf U_n^{*}\bigg)^{-1}\bigg\} \\[5pt] & \quad - \frac{1}{p}\mathbb E\operatorname{tr}\mathcal B_{n}^{-1}\textbf T^{l}_n(\textbf K - z\textbf I_p)^{-1} \textbf K + o(1) \\[5pt] & = \frac{1}{np}\sum_{k=1}^n\mathbb E \big\{\operatorname{tr}\mathcal B_{k,n}^{-1}\textbf T_n^{l}(\textbf K - z\textbf I_p)^{-1}\textbf K\big\} - \frac{1}{p}\mathbb E\operatorname{tr}\mathcal B_{n}^{-1}\textbf T^{l}_n(\textbf K - z\textbf I_p)^{-1} \textbf K + o(1) \\[5pt] & = \frac{1}{np}\sum_{k=1}^n\big\{\mathbb E\operatorname{tr}\mathcal B_{k,n}^{-1}\textbf T_n^{l} (\textbf K - z\textbf I_p)^{-1}\textbf K - \mathbb E\operatorname{tr}\mathcal B_{n}^{-1}\textbf T^{l}_n(\textbf K - z\textbf I_p)^{-1} \textbf K\big\} + o(1) = o(1), \end{align*}
where for the last equality we used Lemma 1 again. Finally, we deduce that, for
![]() $l=0, 1$
,
$l=0, 1$
,
Write
 \begin{align*} (\textbf K -z\textbf I_p)^{-1} & = \bigg(\frac{\textbf U_n\boldsymbol{\widetilde\Sigma}_\pi\textbf U_n^{*}} {1 + ({m}/{n})\mathbb E\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1}\textbf U_n \boldsymbol{\Sigma}_\pi} - z\textbf I_p\bigg)^{-1} \\[5pt] & = \bigg(\frac{\textbf T_n} {1 + ({m}/{n})\mathbb E\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1}\textbf U_n \boldsymbol{\Sigma}_\pi} - z\textbf I_p - \frac{({1}/{m})\textbf U_n\textbf{1}\textbf{1}^{*}\textbf U_n^{*}} {1 + ({m}/{n})\mathbb E\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1}\textbf U_n \boldsymbol{\Sigma}_\pi}\bigg)^{-1}. \end{align*}
\begin{align*} (\textbf K -z\textbf I_p)^{-1} & = \bigg(\frac{\textbf U_n\boldsymbol{\widetilde\Sigma}_\pi\textbf U_n^{*}} {1 + ({m}/{n})\mathbb E\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1}\textbf U_n \boldsymbol{\Sigma}_\pi} - z\textbf I_p\bigg)^{-1} \\[5pt] & = \bigg(\frac{\textbf T_n} {1 + ({m}/{n})\mathbb E\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1}\textbf U_n \boldsymbol{\Sigma}_\pi} - z\textbf I_p - \frac{({1}/{m})\textbf U_n\textbf{1}\textbf{1}^{*}\textbf U_n^{*}} {1 + ({m}/{n})\mathbb E\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1}\textbf U_n \boldsymbol{\Sigma}_\pi}\bigg)^{-1}. \end{align*}
For any real
![]() $\lambda >0$
, it is easy to show that
$\lambda >0$
, it is easy to show that
Then, we can check that
 \begin{align*} \bigg\|\bigg(\frac{\textbf T_n} {1 + ({m}/{n})\mathbb E\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1}\textbf U_n \boldsymbol{\Sigma}_\pi} - z\textbf I_p\bigg)^{-1}\bigg\| & \leq \max_{t \ge 0}\bigg\vert\frac{t} {1 + ({m}/{n})\mathbb E\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1}\textbf U_n \boldsymbol{\Sigma}_\pi} - z\bigg\vert^{-1} \\[5pt] & \leq \max_{t \ge 0}\bigg\vert\frac{1 + ({m}/{n})\mathbb E\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1}\textbf U_n\boldsymbol{\Sigma}_\pi} {t-z(1+({m}/{n})\mathbb E\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1}\textbf U_n \boldsymbol{\Sigma}_\pi)}\bigg\vert \leq L/v, \end{align*}
\begin{align*} \bigg\|\bigg(\frac{\textbf T_n} {1 + ({m}/{n})\mathbb E\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1}\textbf U_n \boldsymbol{\Sigma}_\pi} - z\textbf I_p\bigg)^{-1}\bigg\| & \leq \max_{t \ge 0}\bigg\vert\frac{t} {1 + ({m}/{n})\mathbb E\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1}\textbf U_n \boldsymbol{\Sigma}_\pi} - z\bigg\vert^{-1} \\[5pt] & \leq \max_{t \ge 0}\bigg\vert\frac{1 + ({m}/{n})\mathbb E\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1}\textbf U_n\boldsymbol{\Sigma}_\pi} {t-z(1+({m}/{n})\mathbb E\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1}\textbf U_n \boldsymbol{\Sigma}_\pi)}\bigg\vert \leq L/v, \end{align*}
where the constant L may change from one appearance to the next. Consequently, we could find that
By using (21) from Lemma 3 and (14), we can show that
Similarly, by using (21) from Lemma 3 again and Lemma 4, we have
![]() $\|(\textbf K -z\textbf I_p)^{-1}\| \leq L$
. Thus, we obtain
$\|(\textbf K -z\textbf I_p)^{-1}\| \leq L$
. Thus, we obtain
 \begin{equation} \bigg\vert\frac{1}{p} \frac{\mathbb E\operatorname{tr}({1}/{m})\textbf U_n\textbf 1\textbf 1^{*}\textbf U_n^{*} (\textbf{K} - z\textbf I_p)^{-1}} {1 + ({m}/{n})\mathbb E\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1}\textbf U_n\boldsymbol{\Sigma}_\pi} \Bigg\vert \to 0. \end{equation}
\begin{equation} \bigg\vert\frac{1}{p} \frac{\mathbb E\operatorname{tr}({1}/{m})\textbf U_n\textbf 1\textbf 1^{*}\textbf U_n^{*} (\textbf{K} - z\textbf I_p)^{-1}} {1 + ({m}/{n})\mathbb E\operatorname{tr}\textbf U_n^{*}\mathcal{B}_{n}^{-1}\textbf U_n\boldsymbol{\Sigma}_\pi} \Bigg\vert \to 0. \end{equation}
Notice that
By (16) we obtain
as
![]() $n\to\infty$
. Then, combining (13), (15), and (17), it follows that
$n\to\infty$
. Then, combining (13), (15), and (17), it follows that
where we utilized the identity relation between
![]() $\boldsymbol{\Sigma}_\pi$
and
$\boldsymbol{\Sigma}_\pi$
and
![]() $\boldsymbol{\widetilde\Sigma}_\pi$
. Consequently, we deduce that
$\boldsymbol{\widetilde\Sigma}_\pi$
. Consequently, we deduce that
Substituting this into (15), we obtain
For any fixed
![]() $z\in\mathbb C^+$
,
$z\in\mathbb C^+$
,
![]() $\mathbb{E} s_n(z)=p^{-1}\mathbb{E}\operatorname{tr}\mathcal{B}_n^{-1}$
is a bounded sequence. Thus, for any subsequence
$\mathbb{E} s_n(z)=p^{-1}\mathbb{E}\operatorname{tr}\mathcal{B}_n^{-1}$
is a bounded sequence. Thus, for any subsequence
![]() $\{n'\}$
, there is a subsubsequence
$\{n'\}$
, there is a subsubsequence
![]() $\{n''\}$
such that
$\{n''\}$
such that
![]() $\mathbb E s_{n^{\prime\prime}}(z)$
converges to a limit s(z). Then, from (18), s(z) satisfies
$\mathbb E s_{n^{\prime\prime}}(z)$
converges to a limit s(z). Then, from (18), s(z) satisfies
In [Reference Silverstein22], it is proved that for any
![]() $z\in\mathbb C^+$
(19) has a unique solution in
$z\in\mathbb C^+$
(19) has a unique solution in
![]() $\mathbb C^+$
. Thus, we conclude that
$\mathbb C^+$
. Thus, we conclude that
![]() $\mathbb{E} s_n(z) $
tends to a unique s(z). We have therefore finished the proof of Theorem 1.
$\mathbb{E} s_n(z) $
tends to a unique s(z). We have therefore finished the proof of Theorem 1.
Appendix A. Supporting results
In this appendix we list some results that are needed in the proof.
Lemma 1. ([Reference Silverstein and Bai24, Lemma 2.6].) Let
![]() $\textbf A$
and
$\textbf A$
and
![]() $\textbf C$
be
$\textbf C$
be
![]() $p \times p$
Hermitian matrices. For
$p \times p$
Hermitian matrices. For
![]() $\tau \in \mathbb R$
,
$\tau \in \mathbb R$
,
![]() $q \in \mathbb C^{p}$
, and
$q \in \mathbb C^{p}$
, and
![]() $z=u+{\mathrm{i}} v \in\mathbb C^+$
,
$z=u+{\mathrm{i}} v \in\mathbb C^+$
,
Lemma 2. (Burkholder inequality in [Reference Bai and Silverstein3, Lemma 2.12].) Let
![]() $\{\textbf X_k\}$
be a complex martingale difference sequence with respect to the increasing
$\{\textbf X_k\}$
be a complex martingale difference sequence with respect to the increasing
![]() $\sigma$
-field
$\sigma$
-field
![]() $\{{F}_k\}$
. Then, for
$\{{F}_k\}$
. Then, for
![]() $q>1$
,
$q>1$
,
Lemma 3. For any
![]() $z\in\mathbb{C}$
with
$z\in\mathbb{C}$
with
![]() ${\mathrm{Im}}(z)\neq0$
, any Hermitian matrix
${\mathrm{Im}}(z)\neq0$
, any Hermitian matrix
![]() $\textbf C\in\mathbb{C}^{p\times p}$
, and
$\textbf C\in\mathbb{C}^{p\times p}$
, and
![]() $\boldsymbol{\alpha},\boldsymbol{\beta}\in\mathbb{C}^p$
where
$\boldsymbol{\alpha},\boldsymbol{\beta}\in\mathbb{C}^p$
where
![]() $\textbf{C}+\boldsymbol{\alpha}\boldsymbol{\alpha}^{*}-z\textbf{I}_p$
,
$\textbf{C}+\boldsymbol{\alpha}\boldsymbol{\alpha}^{*}-z\textbf{I}_p$
,
![]() $\textbf{C}+\boldsymbol{\alpha}\boldsymbol{\beta}^{*}-z\textbf{I}_p$
, and
$\textbf{C}+\boldsymbol{\alpha}\boldsymbol{\beta}^{*}-z\textbf{I}_p$
, and
![]() $\textbf{C}-z\textbf{I}_p$
are invertible, we have
$\textbf{C}-z\textbf{I}_p$
are invertible, we have
The formula in (20) can be regarded as a special case of [Reference Silverstein and Bai24, (2.2)], and (21) is a direct result of the resolvent identity
where
![]() $\textbf{A}$
is a
$\textbf{A}$
is a
![]() $p \times p$
Hermitian matrix and
$p \times p$
Hermitian matrix and
![]() $\textbf{p}, \textbf{q} \in \mathbb C^{p}$
.
$\textbf{p}, \textbf{q} \in \mathbb C^{p}$
.
Lemma 4. (Weyl’s inequality) Let
![]() $\textbf A$
and
$\textbf A$
and
![]() $\textbf C$
be
$\textbf C$
be
![]() $p \times p$
Hermitian matrices. Let
$p \times p$
Hermitian matrices. Let
![]() $\lambda_{1}(\textbf{C}) \geq \lambda_{2}(\textbf{C}) \geq \cdots \geq \lambda_{p}(\textbf{C})$
denote the p eigenvalues of
$\lambda_{1}(\textbf{C}) \geq \lambda_{2}(\textbf{C}) \geq \cdots \geq \lambda_{p}(\textbf{C})$
denote the p eigenvalues of
![]() $\textbf C$
, and
$\textbf C$
, and
![]() $\lambda_{i}(\textbf{A})$
the ith eigenvalue of
$\lambda_{i}(\textbf{A})$
the ith eigenvalue of
![]() $\textbf A$
. Then
$\textbf A$
. Then
![]() $\lambda_{i}(\textbf{A}) + \lambda_{p}(\textbf{C}) \leq \lambda_{i}(\textbf{A} + \textbf{C}) \leq \lambda_{i}(\textbf{A}) + \lambda_{1}(\textbf{C})$
.
$\lambda_{i}(\textbf{A}) + \lambda_{p}(\textbf{C}) \leq \lambda_{i}(\textbf{A} + \textbf{C}) \leq \lambda_{i}(\textbf{A}) + \lambda_{1}(\textbf{C})$
.
Proof of (11). Before proceeding, let us introduce some notation. Let
![]() $\textbf{e}_k$
be the
$\textbf{e}_k$
be the
![]() $m \times 1$
vector with the kth element being 1 and the others zero. In addition, we will use Assumption 3 repeatedly, often without mention. For
$m \times 1$
vector with the kth element being 1 and the others zero. In addition, we will use Assumption 3 repeatedly, often without mention. For
![]() $k=1,\ldots,n$
, let
$k=1,\ldots,n$
, let
 \begin{equation*} \sigma_{il} = \begin{cases} \mathbb E x_{\pi_{i}^{(k)},k}\overline{x}_{\pi_{l}^{(k)},k} = \mathbb E\dfrac{{\sum_{i \ne l}^m{x_{ik}}\overline{x}_{lk}}}{{m({m - 1})}} = \dfrac{{-1}}{{m({m - 1})}}, & i \ne l; \\[9pt] \mathbb E x_{\pi_{i}^{(k)},k}\overline{x}_{\pi_{i}^{(k)},k} = \mathbb E\dfrac{{\sum_{i = 1}^m{x_{ik}\overline{x}_{ik}}}}{m} = \dfrac{1}{m}, & i=l. \end{cases} \end{equation*}
\begin{equation*} \sigma_{il} = \begin{cases} \mathbb E x_{\pi_{i}^{(k)},k}\overline{x}_{\pi_{l}^{(k)},k} = \mathbb E\dfrac{{\sum_{i \ne l}^m{x_{ik}}\overline{x}_{lk}}}{{m({m - 1})}} = \dfrac{{-1}}{{m({m - 1})}}, & i \ne l; \\[9pt] \mathbb E x_{\pi_{i}^{(k)},k}\overline{x}_{\pi_{i}^{(k)},k} = \mathbb E\dfrac{{\sum_{i = 1}^m{x_{ik}\overline{x}_{ik}}}}{m} = \dfrac{1}{m}, & i=l. \end{cases} \end{equation*}
We start with the quantity
 \begin{align*} & \mathbb E\Bigg\vert{\sum_{i=1}^m{\sum_{l=1}^m{b_{il}}} \big({\overline{x}_{\pi_i^{(k)},k}x_{\pi_l^{(k)},k} - \sigma_{il}}\big)}\Bigg\vert^2 = \\[5pt] & \quad \sum_{i_1=1}^{m}\sum_{i_2=1}^{m}\sum_{l_1=1}^{m}\sum_{l_2=1}^{m}b_{i_1l_1}\overline{b}_{i_2l_2} \mathbb E\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{l_1}^{(k)},k} - \sigma_{i_1l_1}}\big) \big({x_{\pi_{i_2}^{(k)},k}\overline{x}_{\pi_{l_2}^{(k)},k} - \sigma_{i_2l_2}}\big). \end{align*}
\begin{align*} & \mathbb E\Bigg\vert{\sum_{i=1}^m{\sum_{l=1}^m{b_{il}}} \big({\overline{x}_{\pi_i^{(k)},k}x_{\pi_l^{(k)},k} - \sigma_{il}}\big)}\Bigg\vert^2 = \\[5pt] & \quad \sum_{i_1=1}^{m}\sum_{i_2=1}^{m}\sum_{l_1=1}^{m}\sum_{l_2=1}^{m}b_{i_1l_1}\overline{b}_{i_2l_2} \mathbb E\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{l_1}^{(k)},k} - \sigma_{i_1l_1}}\big) \big({x_{\pi_{i_2}^{(k)},k}\overline{x}_{\pi_{l_2}^{(k)},k} - \sigma_{i_2l_2}}\big). \end{align*}
Note that the matrix
![]() $\textbf{B} = \textbf U_n^{*}\mathcal B_{k,n}^{-1} \textbf U_n = (b_{il})$
is independent of
$\textbf{B} = \textbf U_n^{*}\mathcal B_{k,n}^{-1} \textbf U_n = (b_{il})$
is independent of
![]() $\textbf x_{\pi^{(k)}}$
, and its spectral norm is uniformly bounded. In this expression, the random variables with the same first index (i, l) are dependent. Thus there are now five cases, depending on how many distinct indices there are among them.
$\textbf x_{\pi^{(k)}}$
, and its spectral norm is uniformly bounded. In this expression, the random variables with the same first index (i, l) are dependent. Thus there are now five cases, depending on how many distinct indices there are among them.
One unique index:
![]() $i_1= i_2 =l_1 = l_2$
. In this case, we can write the summation as
$i_1= i_2 =l_1 = l_2$
. In this case, we can write the summation as
where
Here we used the condition
![]() $\sum_{i=1}^m{\mathbb{E}\vert x_{ik}\vert^4} \to 0$
$\sum_{i=1}^m{\mathbb{E}\vert x_{ik}\vert^4} \to 0$
![]() $(k=1,\ldots,n)$
. Note that
$(k=1,\ldots,n)$
. Note that
Thus, we conclude that
![]() $\mbox{I} = o(1)$
.
$\mbox{I} = o(1)$
.
Two distinct indices.
![]() $i_1= i_2 =l_1 \neq l_2$
and
$i_1= i_2 =l_1 \neq l_2$
and
![]() $i_1= i_2 =l_2 \neq l_1$
are symmetric cases;
$i_1= i_2 =l_2 \neq l_1$
are symmetric cases;
![]() $i_1= l_2 =l_1 \neq i_2$
and
$i_1= l_2 =l_1 \neq i_2$
and
![]() $l_1= i_2 =l_2 \neq i_1$
are symmetric cases. Then we have that
$l_1= i_2 =l_2 \neq i_1$
are symmetric cases. Then we have that
 \begin{align*} \mbox{II} & = 2\sum_{i_1=i_2=l_2\neq l_1}^m{b_{i_1l_1}\overline{b}_{i_1i_1}} \cdot \mathbb{E}\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{l_1}^{(k)},k} - \sigma_{i_1l_1}}\big) \big({x_{\pi_{i_1}^{(k)},k}\overline{x}_{\pi_{i_1}^{(k)},k} - \sigma_{i_1i_1}}\big) \\[5pt] & \quad + 2\sum_{l_1=i_2=l_2\neq i_1}^m{b_{i_1l_1}\overline{b}_{l_1l_1}} \cdot \mathbb{E}\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{l_1}^{(k)},k} - \sigma_{i_1l_1}}\big) \big({x_{\pi_{l_1}^{(k)},k}\overline{x}_{\pi_{l_1}^{(k)},k} - \sigma_{l_1l_1}}\big), \end{align*}
\begin{align*} \mbox{II} & = 2\sum_{i_1=i_2=l_2\neq l_1}^m{b_{i_1l_1}\overline{b}_{i_1i_1}} \cdot \mathbb{E}\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{l_1}^{(k)},k} - \sigma_{i_1l_1}}\big) \big({x_{\pi_{i_1}^{(k)},k}\overline{x}_{\pi_{i_1}^{(k)},k} - \sigma_{i_1i_1}}\big) \\[5pt] & \quad + 2\sum_{l_1=i_2=l_2\neq i_1}^m{b_{i_1l_1}\overline{b}_{l_1l_1}} \cdot \mathbb{E}\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{l_1}^{(k)},k} - \sigma_{i_1l_1}}\big) \big({x_{\pi_{l_1}^{(k)},k}\overline{x}_{\pi_{l_1}^{(k)},k} - \sigma_{l_1l_1}}\big), \end{align*}
where for
![]() $i_1 \ne l_1$
we have
$i_1 \ne l_1$
we have
 \begin{align*} \mathbb{E}\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{l_1}^{(k)},k} - \sigma_{i_1l_1}}\big) \big({x_{\pi_{l_1}^{(k)},k}\overline{x}_{\pi_{l_1}^{(k)},k} - \sigma_{l_1l_1}}\big) & = \mathbb{E}\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{l_1}^{(k)},k} - \sigma_{i_1l_1}}\big) \big({x_{\pi_{i_1}^{(k)},k}\overline{x}_{\pi_{i_1}^{(k)},k} - \sigma_{i_1i_1}}\big) \\[5pt] & = \mathbb{E}x_{\pi_{i_1}^{(k)},k}(\overline{x}_{\pi_{i_1}^{(k)},k})^2x_{\pi_{l_1}^{(k)},k} - \frac{{-1}}{{m^2(m - 1)}} \\[5pt] & = \frac{{-\mathbb{E}\sum_{i_1=1}^m{\vert x_{i_1k}\vert^4}}}{{m(m - 1)}} - \frac{{-1}}{{m^2(m - 1)}} \\[5pt] & = \frac{{1}}{{m^2(m - 1)}} + o(1/m^2). \end{align*}
\begin{align*} \mathbb{E}\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{l_1}^{(k)},k} - \sigma_{i_1l_1}}\big) \big({x_{\pi_{l_1}^{(k)},k}\overline{x}_{\pi_{l_1}^{(k)},k} - \sigma_{l_1l_1}}\big) & = \mathbb{E}\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{l_1}^{(k)},k} - \sigma_{i_1l_1}}\big) \big({x_{\pi_{i_1}^{(k)},k}\overline{x}_{\pi_{i_1}^{(k)},k} - \sigma_{i_1i_1}}\big) \\[5pt] & = \mathbb{E}x_{\pi_{i_1}^{(k)},k}(\overline{x}_{\pi_{i_1}^{(k)},k})^2x_{\pi_{l_1}^{(k)},k} - \frac{{-1}}{{m^2(m - 1)}} \\[5pt] & = \frac{{-\mathbb{E}\sum_{i_1=1}^m{\vert x_{i_1k}\vert^4}}}{{m(m - 1)}} - \frac{{-1}}{{m^2(m - 1)}} \\[5pt] & = \frac{{1}}{{m^2(m - 1)}} + o(1/m^2). \end{align*}
Note that
 \begin{equation*} \Bigg\vert\sum_{i_1\neq l_1}b_{i_1l_1}\overline{b}_{l_1l_1}\Bigg\vert = \Bigg\vert\sum_{i_1\neq l_1}b_{i_1l_1}\overline{b}_{i_1i_1}\Bigg\vert = \Bigg\vert\sum_{i_1=1}^{m}\overline{b}_{i_1i_1} \cdot \textbf{e}_{i_1}^{*}\textbf{B}(\textbf{1}-\textbf{e}_{i_1})\Bigg\vert \leq m^{2}\|\overline{\textbf{B}}\| \cdot \|\textbf{B}\|. \end{equation*}
\begin{equation*} \Bigg\vert\sum_{i_1\neq l_1}b_{i_1l_1}\overline{b}_{l_1l_1}\Bigg\vert = \Bigg\vert\sum_{i_1\neq l_1}b_{i_1l_1}\overline{b}_{i_1i_1}\Bigg\vert = \Bigg\vert\sum_{i_1=1}^{m}\overline{b}_{i_1i_1} \cdot \textbf{e}_{i_1}^{*}\textbf{B}(\textbf{1}-\textbf{e}_{i_1})\Bigg\vert \leq m^{2}\|\overline{\textbf{B}}\| \cdot \|\textbf{B}\|. \end{equation*}
Thus, we obtain
![]() $\mbox{II} = o(1)$
.
$\mbox{II} = o(1)$
.
Two distinct indices:
![]() $i_1= i_2 \neq l_1=l_2$
,
$i_1= i_2 \neq l_1=l_2$
,
![]() $i_1= l_1 \neq l_2=i_2$
, and
$i_1= l_1 \neq l_2=i_2$
, and
![]() $i_1= l_2 \neq i_2=l_1$
. Here we could simplify the summation as
$i_1= l_2 \neq i_2=l_1$
. Here we could simplify the summation as
![]() $\mbox{III} = \mbox{III}_1 + \mbox{III}_2 + \mbox{III}_3$
, where
$\mbox{III} = \mbox{III}_1 + \mbox{III}_2 + \mbox{III}_3$
, where
 \begin{align*} \mbox{III}_1 & = \sum_{i_1=i_2\neq l_1=l_2}^m\vert{b_{i_1l_1}\vert^2} \cdot \mathbb{E}\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{l_1}^{(k)},k} - \sigma_{i_1l_1}}\big)^2; \\[5pt] \mbox{III}_2 & = \sum_{i_1=l_1\neq l_2=i_2}^m{b_{i_1i_1}\overline{b}_{i_2i_2}} \cdot \mathbb{E}\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{i_1}^{(k)},k} - \sigma_{i_1i_1}}\big) \big({\overline{x}_{\pi_{i_2}^{(k)},k}x_{\pi_{i_2}^{(k)},k} - \sigma_{i_2i_2}}); \\[5pt] \mbox{III}_3 & = \sum_{i_1=l_2\neq i_2=l_1}^m{b_{i_1i_2}\overline{b}_{i_2i_1}} \cdot \mathbb{E}\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{i_2}^{(k)},k} - \sigma_{i_1i_2}}\big) \big({x_{\pi_{i_2}^{(k)},k}\overline{x}_{\pi_{i_1}^{(k)},k} - \sigma_{i_2i_1}}\big). \end{align*}
\begin{align*} \mbox{III}_1 & = \sum_{i_1=i_2\neq l_1=l_2}^m\vert{b_{i_1l_1}\vert^2} \cdot \mathbb{E}\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{l_1}^{(k)},k} - \sigma_{i_1l_1}}\big)^2; \\[5pt] \mbox{III}_2 & = \sum_{i_1=l_1\neq l_2=i_2}^m{b_{i_1i_1}\overline{b}_{i_2i_2}} \cdot \mathbb{E}\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{i_1}^{(k)},k} - \sigma_{i_1i_1}}\big) \big({\overline{x}_{\pi_{i_2}^{(k)},k}x_{\pi_{i_2}^{(k)},k} - \sigma_{i_2i_2}}); \\[5pt] \mbox{III}_3 & = \sum_{i_1=l_2\neq i_2=l_1}^m{b_{i_1i_2}\overline{b}_{i_2i_1}} \cdot \mathbb{E}\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{i_2}^{(k)},k} - \sigma_{i_1i_2}}\big) \big({x_{\pi_{i_2}^{(k)},k}\overline{x}_{\pi_{i_1}^{(k)},k} - \sigma_{i_2i_1}}\big). \end{align*}
When
![]() $i_1 \ne i_2$
, we can write
$i_1 \ne i_2$
, we can write
 \begin{align*} \mathbb{E}\big({x_{\pi_{i_1}^{(k)},k}\overline{x}_{\pi_{i_2}^{(k)},k} - \sigma_{i_1i_2}}\big)^2 &= \mathbb{E}x_{\pi_{i_1}^{(k)},k}^2\big(\overline{x}_{\pi_{i_2}^{(k)},k}\big)^2 - \sigma_{i_1i_2}^2\\[5pt] & = \frac{{\mathbb E\sum_{i_1\ne i_2}^p{x^2_{i_1 k}(\overline{x}_{i_2 k})^2}}}{{m(m - 1)}} - \frac{1}{{m^2(m - 1)^2}} = O(m^{-2}); \end{align*}
\begin{align*} \mathbb{E}\big({x_{\pi_{i_1}^{(k)},k}\overline{x}_{\pi_{i_2}^{(k)},k} - \sigma_{i_1i_2}}\big)^2 &= \mathbb{E}x_{\pi_{i_1}^{(k)},k}^2\big(\overline{x}_{\pi_{i_2}^{(k)},k}\big)^2 - \sigma_{i_1i_2}^2\\[5pt] & = \frac{{\mathbb E\sum_{i_1\ne i_2}^p{x^2_{i_1 k}(\overline{x}_{i_2 k})^2}}}{{m(m - 1)}} - \frac{1}{{m^2(m - 1)^2}} = O(m^{-2}); \end{align*}
 \begin{align*} \mathbb{E}\big({x_{\pi_{i_1}^{(k)},k}\overline{x}_{\pi_{i_1}^{(k)},k} - \sigma_{i_1i_1}}\big) \big({x_{\pi_{i_2}^{(k)},k}\overline{x}_{\pi_{i_2}^{(k)},k} - \sigma_{i_2i_2}}\big) & = \mathbb{E}{\big\vert x_{\pi_{i_1}^{(k)},k}\big\vert^2\big\vert x_{\pi_{i_2}^{(k)},k}\big\vert^2} - \sigma_{i_1i_1}\sigma_{i_2i_2} \\[5pt] & = \frac{{\mathbb E\sum_{i_1\ne i_2 }^m{\vert x_{i_1 k}\vert^2\vert x_{i_2 k}\vert^2}}}{{m(m - 1)}} - \frac{1}{{m^2}} \\[5pt] & = \frac{{\mathbb E\big({\sum_{i_1=1}^m{\vert x_{i_1 k}\vert^2}}\big)^2 - \mathbb E\big({\sum_{i_1=1}^m{\vert x_{i_1 k}}\vert^4}\big)}}{{m(m - 1)}} - \frac{1}{{m^2}}\\[5pt] &= o(1/m^2). \end{align*}
\begin{align*} \mathbb{E}\big({x_{\pi_{i_1}^{(k)},k}\overline{x}_{\pi_{i_1}^{(k)},k} - \sigma_{i_1i_1}}\big) \big({x_{\pi_{i_2}^{(k)},k}\overline{x}_{\pi_{i_2}^{(k)},k} - \sigma_{i_2i_2}}\big) & = \mathbb{E}{\big\vert x_{\pi_{i_1}^{(k)},k}\big\vert^2\big\vert x_{\pi_{i_2}^{(k)},k}\big\vert^2} - \sigma_{i_1i_1}\sigma_{i_2i_2} \\[5pt] & = \frac{{\mathbb E\sum_{i_1\ne i_2 }^m{\vert x_{i_1 k}\vert^2\vert x_{i_2 k}\vert^2}}}{{m(m - 1)}} - \frac{1}{{m^2}} \\[5pt] & = \frac{{\mathbb E\big({\sum_{i_1=1}^m{\vert x_{i_1 k}\vert^2}}\big)^2 - \mathbb E\big({\sum_{i_1=1}^m{\vert x_{i_1 k}}\vert^4}\big)}}{{m(m - 1)}} - \frac{1}{{m^2}}\\[5pt] &= o(1/m^2). \end{align*}
Here,
![]() $\mbox{III}_2 = o(1)$
follows from the fact that
$\mbox{III}_2 = o(1)$
follows from the fact that
![]() $\mathbb E{\sum_{i_1=1}^m{\vert x_{i_1 k}\vert^2}} = 1$
. As to the term
$\mathbb E{\sum_{i_1=1}^m{\vert x_{i_1 k}\vert^2}} = 1$
. As to the term
![]() $\mathbb{E}x_{\pi_{i_1}^{(k)},k}^2\big(\overline{x}_{\pi_{i_2}^{(k)},k}\big)^2$
, we check that
$\mathbb{E}x_{\pi_{i_1}^{(k)},k}^2\big(\overline{x}_{\pi_{i_2}^{(k)},k}\big)^2$
, we check that
 \begin{equation} \Bigg\vert\mathbb E\sum_{i_1,i_2}{x^2_{i_1 k}(\overline{x}_{i_2 k})^2}\Bigg\vert \leq \mathbb E\sum_{i_1,i_2}\vert x^2_{i_1 k}\vert\vert\overline{x}_{i_2 k}\vert^2 \leq 1. \end{equation}
\begin{equation} \Bigg\vert\mathbb E\sum_{i_1,i_2}{x^2_{i_1 k}(\overline{x}_{i_2 k})^2}\Bigg\vert \leq \mathbb E\sum_{i_1,i_2}\vert x^2_{i_1 k}\vert\vert\overline{x}_{i_2 k}\vert^2 \leq 1. \end{equation}
Note that
 \begin{align*} \sum_{i_1\neq l_1}\vert b_{i_1l_1}\vert^{2} & = \Bigg\vert\operatorname{tr}\textbf{B}\textbf{B}^{*} - \sum_{i_1=1}^{m}\vert b_{i_1i_1}\vert^{2}\Bigg\vert \leq Lm\|\overline{\textbf{B}}\|\cdot\|\textbf{B}\|, \\[5pt] \Bigg\vert\sum_{i_1\neq l_1}b_{i_1i_2}\overline{b}_{i_2i_1}\Bigg\vert & = \Bigg\vert\operatorname{tr}\textbf{B}\overline{\textbf{B}} - \sum_{i=1}^{m}\vert b_{i_1i_1}\vert^{2}\Bigg\vert \leq Lm\|\overline{\textbf{B}}\|\cdot\|\textbf{B}\|. \end{align*}
\begin{align*} \sum_{i_1\neq l_1}\vert b_{i_1l_1}\vert^{2} & = \Bigg\vert\operatorname{tr}\textbf{B}\textbf{B}^{*} - \sum_{i_1=1}^{m}\vert b_{i_1i_1}\vert^{2}\Bigg\vert \leq Lm\|\overline{\textbf{B}}\|\cdot\|\textbf{B}\|, \\[5pt] \Bigg\vert\sum_{i_1\neq l_1}b_{i_1i_2}\overline{b}_{i_2i_1}\Bigg\vert & = \Bigg\vert\operatorname{tr}\textbf{B}\overline{\textbf{B}} - \sum_{i=1}^{m}\vert b_{i_1i_1}\vert^{2}\Bigg\vert \leq Lm\|\overline{\textbf{B}}\|\cdot\|\textbf{B}\|. \end{align*}
Thus, as
![]() $m \to \infty$
, we could obtain
$m \to \infty$
, we could obtain
 \begin{align*} \mbox{III}_1 + \mbox{III}_3 \leq \sum_{i_1\neq l_1}^m{b_{i_1l_1}\overline{b}_{i_1l_1}}\big\vert\mathbb{E}x_{\pi_{i_1}^{(k)},k}^2 \big(\overline{x}_{\pi_{l_1}^{(k)},k}\big)^2\big\vert + \sum_{i_1\neq i_2}^m{b_{i_1i_2}\overline{b}_{i_2i_1}}\big\vert\mathbb{E}x_{\pi_{i_1}^{(k)},k}^2 \big(\overline{x}_{\pi_{i_2}^{(k)},k}\big)^2\big\vert = o(1). \end{align*}
\begin{align*} \mbox{III}_1 + \mbox{III}_3 \leq \sum_{i_1\neq l_1}^m{b_{i_1l_1}\overline{b}_{i_1l_1}}\big\vert\mathbb{E}x_{\pi_{i_1}^{(k)},k}^2 \big(\overline{x}_{\pi_{l_1}^{(k)},k}\big)^2\big\vert + \sum_{i_1\neq i_2}^m{b_{i_1i_2}\overline{b}_{i_2i_1}}\big\vert\mathbb{E}x_{\pi_{i_1}^{(k)},k}^2 \big(\overline{x}_{\pi_{i_2}^{(k)},k}\big)^2\big\vert = o(1). \end{align*}
Eventually, we get
![]() $\mbox{III} = o(1)$
.
$\mbox{III} = o(1)$
.
Three distinct indices. In this case, we divide it into six classes, writing
![]() $\mathcal{I}_{1} = \{i_1 = i_2$
, other indices different
$\mathcal{I}_{1} = \{i_1 = i_2$
, other indices different
![]() $\}$
;
$\}$
;
![]() $\mathcal{I}_{2} = \{i_1 = l_1$
, other indices different
$\mathcal{I}_{2} = \{i_1 = l_1$
, other indices different
![]() $\}$
;
$\}$
;
![]() $\mathcal{I}_{3} = \{i_1 = l_2$
, other indices different
$\mathcal{I}_{3} = \{i_1 = l_2$
, other indices different
![]() $\}$
;
$\}$
;
![]() $\mathcal{I}_{4} = \{l_1 = i_2$
, other indices different
$\mathcal{I}_{4} = \{l_1 = i_2$
, other indices different
![]() $\}$
;
$\}$
;
![]() $\mathcal{I}_{5} = \{i_2 = l_2$
, other indices different
$\mathcal{I}_{5} = \{i_2 = l_2$
, other indices different
![]() $\}$
; and
$\}$
; and
![]() $\mathcal{I}_{6} = \{l_1 = l_2$
, other indices different
$\mathcal{I}_{6} = \{l_1 = l_2$
, other indices different
![]() $\}$
. In what follows, we proceed to deal with the summation of three distinct indices,
$\}$
. In what follows, we proceed to deal with the summation of three distinct indices,
![]() $\mbox{IV} = \mbox{IV}_1 + \mbox{IV}_2 + \mbox{IV}_3 + \mbox{IV}_4 + \mbox{IV}_5 + \mbox{IV}_6$
. Here,
$\mbox{IV} = \mbox{IV}_1 + \mbox{IV}_2 + \mbox{IV}_3 + \mbox{IV}_4 + \mbox{IV}_5 + \mbox{IV}_6$
. Here,
 \begin{align*} \mbox{IV}_1 & = \sum_{l_1,i_1,i_2,l_2\in\mathcal{I}_{1}}^m{b_{i_1l_1}\overline{b}_{i_1l_2}} \cdot \mathbb E\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{l_1}^{(k)},k} - \sigma_{i_1l_1}}\big) \big({x_{\pi_{i1}^{(k)},k}\overline{x}_{\pi_{l_2}^{(k)},k} - \sigma_{i_1l_2}}\big); \\[5pt] \mbox{IV}_2 & = \sum_{l_1,i_1,i_2,l_2\in\mathcal{I}_{2}}^m{b_{i_1i_1}\overline{b}_{i_2l_2}} \cdot \mathbb E\big({\big\vert x_{\pi_{i_1}^{(k)},k}\big\vert^2 - \sigma_{i_1i_1}}\big) \big({x_{\pi_{i_2}^{(k)},k}\overline{x}_{\pi_{l_2}^{(k)},k} - \sigma_{i_2l_2}}\big); \\[5pt] \mbox{IV}_3 & = \sum_{l_1,i_1,i_2,l_2\in\mathcal{I}_{3}}^m{b_{i_1l_1}\overline{b}_{i_2i_1}} \cdot \mathbb E\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{l_1}^{(k)},k} - \sigma_{i_1l_1}}\big) \big({x_{\pi_{i_2}^{(k)},k}\overline{x}_{\pi_{i_1}^{(k)},k} - \sigma_{i_2i_1}}\big); \\[5pt] \mbox{IV}_4 & = \sum_{l_1,i_1,i_2,l_2\in\mathcal{I}_{4}}^m{b_{i_1l_1}\overline{b}_{l_1l_2}} \cdot \mathbb E\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{l_1}^{(k)},k} - \sigma_{i_1l_1}}\big) \big({x_{\pi_{l_1}^{(k)},k}\overline{x}_{\pi_{l_2}^{(k)},k} - \sigma_{l_1l_2}}\big); \\[5pt] \mbox{IV}_5 & = \sum_{l_1,i_1,i_2,l_2\in\mathcal{I}_{5}}^m{b_{i_1l_1}\overline{b}_{i_2i_2}} \cdot \mathbb E\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{l_1}^{(k)},k} - \sigma_{i_1l_1}}\big) \big({\big\vert x_{\pi_{i_2}^{(k)},k}\big\vert^2 - \sigma_{i_2i_2}}\big); \\[5pt] \mbox{IV}_6 & = \sum_{l_1,i_1,i_2,l_2\in\mathcal{I}_{6}}^m{b_{i_1l_1}\overline{b}_{i_2l_1}} \cdot \mathbb E\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{l_1}^{(k)},k} - \sigma_{i_1l_1}}\big) \big({x_{\pi_{i_2}^{(k)},k}\overline{x}_{\pi_{l_1}^{(k)},k} - \sigma_{i_2l_1}}\big). \end{align*}
\begin{align*} \mbox{IV}_1 & = \sum_{l_1,i_1,i_2,l_2\in\mathcal{I}_{1}}^m{b_{i_1l_1}\overline{b}_{i_1l_2}} \cdot \mathbb E\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{l_1}^{(k)},k} - \sigma_{i_1l_1}}\big) \big({x_{\pi_{i1}^{(k)},k}\overline{x}_{\pi_{l_2}^{(k)},k} - \sigma_{i_1l_2}}\big); \\[5pt] \mbox{IV}_2 & = \sum_{l_1,i_1,i_2,l_2\in\mathcal{I}_{2}}^m{b_{i_1i_1}\overline{b}_{i_2l_2}} \cdot \mathbb E\big({\big\vert x_{\pi_{i_1}^{(k)},k}\big\vert^2 - \sigma_{i_1i_1}}\big) \big({x_{\pi_{i_2}^{(k)},k}\overline{x}_{\pi_{l_2}^{(k)},k} - \sigma_{i_2l_2}}\big); \\[5pt] \mbox{IV}_3 & = \sum_{l_1,i_1,i_2,l_2\in\mathcal{I}_{3}}^m{b_{i_1l_1}\overline{b}_{i_2i_1}} \cdot \mathbb E\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{l_1}^{(k)},k} - \sigma_{i_1l_1}}\big) \big({x_{\pi_{i_2}^{(k)},k}\overline{x}_{\pi_{i_1}^{(k)},k} - \sigma_{i_2i_1}}\big); \\[5pt] \mbox{IV}_4 & = \sum_{l_1,i_1,i_2,l_2\in\mathcal{I}_{4}}^m{b_{i_1l_1}\overline{b}_{l_1l_2}} \cdot \mathbb E\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{l_1}^{(k)},k} - \sigma_{i_1l_1}}\big) \big({x_{\pi_{l_1}^{(k)},k}\overline{x}_{\pi_{l_2}^{(k)},k} - \sigma_{l_1l_2}}\big); \\[5pt] \mbox{IV}_5 & = \sum_{l_1,i_1,i_2,l_2\in\mathcal{I}_{5}}^m{b_{i_1l_1}\overline{b}_{i_2i_2}} \cdot \mathbb E\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{l_1}^{(k)},k} - \sigma_{i_1l_1}}\big) \big({\big\vert x_{\pi_{i_2}^{(k)},k}\big\vert^2 - \sigma_{i_2i_2}}\big); \\[5pt] \mbox{IV}_6 & = \sum_{l_1,i_1,i_2,l_2\in\mathcal{I}_{6}}^m{b_{i_1l_1}\overline{b}_{i_2l_1}} \cdot \mathbb E\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{l_1}^{(k)},k} - \sigma_{i_1l_1}}\big) \big({x_{\pi_{i_2}^{(k)},k}\overline{x}_{\pi_{l_1}^{(k)},k} - \sigma_{i_2l_1}}\big). \end{align*}
By carefully checking the expectations, we point out that the main components of the above expectations are as follows:
For all
![]() $l_1, i_1, i_2, l_2 \in \mathcal{I}_{1}$
, we have
$l_1, i_1, i_2, l_2 \in \mathcal{I}_{1}$
, we have
 \begin{align*} \mathbb E\big\vert x_{\pi_{i_1}^{(k)},k}\big\vert^2x_{\pi_{l_1}^{(k)},k}\overline{x}_{\pi_{l_2}^{(k)},k} & = \frac{1}{{m(m - 1)(m - 2)}} \mathbb E\sum_{l_1,i_1,i_2,l_2\in\mathcal{I}_{1}}^m{\vert x_{i_1k}\vert^2x_{l_1k}}\overline{x}_{l_2k} \\[5pt] & = -\frac{1}{{m(m - 1)(m - 2)}} \Bigg[\mathbb E\sum_{i_1\ne l_1}^m\vert x_{i_1k}\vert^2\vert x_{l_1k}\vert^2 - \mathbb E\sum_{i_1}^m\vert x_{i_1k}\vert^4\Bigg] = O(m^{-3}), \end{align*}
\begin{align*} \mathbb E\big\vert x_{\pi_{i_1}^{(k)},k}\big\vert^2x_{\pi_{l_1}^{(k)},k}\overline{x}_{\pi_{l_2}^{(k)},k} & = \frac{1}{{m(m - 1)(m - 2)}} \mathbb E\sum_{l_1,i_1,i_2,l_2\in\mathcal{I}_{1}}^m{\vert x_{i_1k}\vert^2x_{l_1k}}\overline{x}_{l_2k} \\[5pt] & = -\frac{1}{{m(m - 1)(m - 2)}} \Bigg[\mathbb E\sum_{i_1\ne l_1}^m\vert x_{i_1k}\vert^2\vert x_{l_1k}\vert^2 - \mathbb E\sum_{i_1}^m\vert x_{i_1k}\vert^4\Bigg] = O(m^{-3}), \end{align*}
where we used the fact that
![]() $\mathbb E{\sum_{i_1=1}^m{\vert x_{i_1k}\vert^2}} = 1$
.
$\mathbb E{\sum_{i_1=1}^m{\vert x_{i_1k}\vert^2}} = 1$
.
For all
![]() $l_1, i_1, i_2, l_2 \in \mathcal{I}_{3}$
, we similarly obtain
$l_1, i_1, i_2, l_2 \in \mathcal{I}_{3}$
, we similarly obtain
 \begin{align*} \mathbb E\big(\overline{x}_{\pi_{i_1}^{(k)},k}\big)^2x_{\pi_{l_1}^{(k)},k}x_{\pi_{i_2}^{(k)},k} & = \frac{1}{{m(m - 1)(m - 2)}} \mathbb E\sum_{l_1,i_1,i_2,l_2\in\mathcal{I}_{3}}^m{(\overline{x}_{i_1k})^2x_{l_1k}}x_{i_2k} \\[5pt] & = -\frac{1}{{m(m - 1)(m - 2)}} \Bigg[\mathbb E\sum_{i_1\ne l_1}^m(\overline{x}_{i_1k})^2x_{l_1k}^2 - \mathbb E\sum_{i_1}^m\vert x_{i_1k}\vert^4\Bigg] = O(m^{-3}), \end{align*}
\begin{align*} \mathbb E\big(\overline{x}_{\pi_{i_1}^{(k)},k}\big)^2x_{\pi_{l_1}^{(k)},k}x_{\pi_{i_2}^{(k)},k} & = \frac{1}{{m(m - 1)(m - 2)}} \mathbb E\sum_{l_1,i_1,i_2,l_2\in\mathcal{I}_{3}}^m{(\overline{x}_{i_1k})^2x_{l_1k}}x_{i_2k} \\[5pt] & = -\frac{1}{{m(m - 1)(m - 2)}} \Bigg[\mathbb E\sum_{i_1\ne l_1}^m(\overline{x}_{i_1k})^2x_{l_1k}^2 - \mathbb E\sum_{i_1}^m\vert x_{i_1k}\vert^4\Bigg] = O(m^{-3}), \end{align*}
where we used (22) again.
And then, for all
![]() $l_1, i_1, i_2, l_2 \in \mathcal{I}_{4}$
,
$l_1, i_1, i_2, l_2 \in \mathcal{I}_{4}$
,
![]() $\mathbb E\big(x_{\pi_{l_1}^{(k)},k}\big)^2\overline{x}_{\pi_{l_2}^{(k)},k}\overline{x}_{\pi_{i_1}^{(k)},k}=O(m^{-3})$
is immediate. Note that
$\mathbb E\big(x_{\pi_{l_1}^{(k)},k}\big)^2\overline{x}_{\pi_{l_2}^{(k)},k}\overline{x}_{\pi_{i_1}^{(k)},k}=O(m^{-3})$
is immediate. Note that
![]() $\mbox{IV}_2 = \overline{\mbox{IV}}_5 = o(1)$
since
$\mbox{IV}_2 = \overline{\mbox{IV}}_5 = o(1)$
since
 \begin{align*} & \Bigg\vert\sum_{l_1,i_1,i_2,l_2\in\mathcal{I}_{2}}^m{b_{i_1i_1}\overline{b}_{i_2l_2}}\Bigg\vert \\[5pt] &\quad = \Bigg\vert\operatorname{tr}\textbf{B}\cdot\textbf{1}^{*}\overline{\textbf{B}}\textbf{1} - \sum_{i_1=l_1=i_2,l_2}^mb_{i_1i_1}\overline{b}_{i_1l_2} - \sum_{i_1=l_1=l_2,i_2}^mb_{i_1i_1}\overline{b}_{i_2i_1} + \sum_{i_1=l_1=i_2=l_2}^mb_{i_1i_1}\overline{b}_{i_1i_1}\Bigg\vert \\[5pt] & \quad = \Bigg\vert\operatorname{tr}\textbf{B}\cdot\textbf{1}^{*}\overline{\textbf{B}}\textbf{1} - \textbf{1}^{*}(\textbf{B}_\mathrm{d}\overline{\textbf{B}})\textbf{1} - \textbf{1}^{*}(\textbf{B}_\mathrm{d}\overline{\textbf{B}})\textbf{1} + \sum_{i=1}^m\vert b_{ii}\vert^2\Bigg\vert = O(m^2), \end{align*}
\begin{align*} & \Bigg\vert\sum_{l_1,i_1,i_2,l_2\in\mathcal{I}_{2}}^m{b_{i_1i_1}\overline{b}_{i_2l_2}}\Bigg\vert \\[5pt] &\quad = \Bigg\vert\operatorname{tr}\textbf{B}\cdot\textbf{1}^{*}\overline{\textbf{B}}\textbf{1} - \sum_{i_1=l_1=i_2,l_2}^mb_{i_1i_1}\overline{b}_{i_1l_2} - \sum_{i_1=l_1=l_2,i_2}^mb_{i_1i_1}\overline{b}_{i_2i_1} + \sum_{i_1=l_1=i_2=l_2}^mb_{i_1i_1}\overline{b}_{i_1i_1}\Bigg\vert \\[5pt] & \quad = \Bigg\vert\operatorname{tr}\textbf{B}\cdot\textbf{1}^{*}\overline{\textbf{B}}\textbf{1} - \textbf{1}^{*}(\textbf{B}_\mathrm{d}\overline{\textbf{B}})\textbf{1} - \textbf{1}^{*}(\textbf{B}_\mathrm{d}\overline{\textbf{B}})\textbf{1} + \sum_{i=1}^m\vert b_{ii}\vert^2\Bigg\vert = O(m^2), \end{align*}
where
![]() $\textbf{B}_\mathrm{d}$
is the diagonal matrix of the diagonal entries of
$\textbf{B}_\mathrm{d}$
is the diagonal matrix of the diagonal entries of
![]() $\textbf{B}$
. Then, we turn to analyze the remainder terms. It follows that
$\textbf{B}$
. Then, we turn to analyze the remainder terms. It follows that
 \begin{align*} \Bigg\vert\sum_{l_1,i_1,i_2,l_2\in\mathcal{I}_{1}}^m{b_{i_1l_1}\overline{b}_{i_1l_2}}\Bigg\vert & = \Bigg\vert\textbf{1}^{*}\textbf{B}\textbf{B}^{*}\textbf{1} - \textbf{1}^{*}\textbf{B}_\mathrm{d}\overline{\textbf{B}}\textbf{1} - \textbf{1}\textbf{B}\overline{\textbf{B}}_\mathrm{d}\textbf{1} + \sum_{i=1}^m\vert b_{ii}\vert^2\Bigg\vert = O(m^2), \\[5pt] \Bigg\vert\sum_{l_1,i_1,i_2,l_2\in\mathcal{I}_{3}}^m{b_{i_1l_1}\overline{b}_{i_2i_1}}\Bigg\vert & = \Bigg\vert\textbf{1}^{*}\textbf{B}\overline{\textbf B}\textbf{1} - \textbf{1}^{*}\textbf{B}\overline{\textbf B}_{\mathrm{d}}\textbf{1} - \textbf{1}^{\ast}\textbf{B}_{\mathrm{d}}\textbf{B}^{\ast}\textbf{1} + \sum_{i=1}^m\vert b_{ii}\vert^2\Bigg\vert = O(m^2). \end{align*}
\begin{align*} \Bigg\vert\sum_{l_1,i_1,i_2,l_2\in\mathcal{I}_{1}}^m{b_{i_1l_1}\overline{b}_{i_1l_2}}\Bigg\vert & = \Bigg\vert\textbf{1}^{*}\textbf{B}\textbf{B}^{*}\textbf{1} - \textbf{1}^{*}\textbf{B}_\mathrm{d}\overline{\textbf{B}}\textbf{1} - \textbf{1}\textbf{B}\overline{\textbf{B}}_\mathrm{d}\textbf{1} + \sum_{i=1}^m\vert b_{ii}\vert^2\Bigg\vert = O(m^2), \\[5pt] \Bigg\vert\sum_{l_1,i_1,i_2,l_2\in\mathcal{I}_{3}}^m{b_{i_1l_1}\overline{b}_{i_2i_1}}\Bigg\vert & = \Bigg\vert\textbf{1}^{*}\textbf{B}\overline{\textbf B}\textbf{1} - \textbf{1}^{*}\textbf{B}\overline{\textbf B}_{\mathrm{d}}\textbf{1} - \textbf{1}^{\ast}\textbf{B}_{\mathrm{d}}\textbf{B}^{\ast}\textbf{1} + \sum_{i=1}^m\vert b_{ii}\vert^2\Bigg\vert = O(m^2). \end{align*}
Similarly, we can obtain
![]() $\big\vert\sum_{l_1,i_1,i_2,l_2\in\mathcal{I}_{4}}^m{b_{i_1l_1}\overline{b}_{i_2i_1}}\big\vert = O(m^2)$
and
$\big\vert\sum_{l_1,i_1,i_2,l_2\in\mathcal{I}_{4}}^m{b_{i_1l_1}\overline{b}_{i_2i_1}}\big\vert = O(m^2)$
and
![]() $\big\vert\sum_{l_1,i_1,i_2,l_2\in\mathcal{I}_{6}}^m{b_{i_1l_1}\overline{b}_{i_2i_1}}\big\vert = O(m^2)$
. Hence,
$\big\vert\sum_{l_1,i_1,i_2,l_2\in\mathcal{I}_{6}}^m{b_{i_1l_1}\overline{b}_{i_2i_1}}\big\vert = O(m^2)$
. Hence,
![]() $\mbox{IV}_1 + \mbox{IV}_3 + \mbox{IV}_4 + \mbox{IV}_6 = O(m^{-1})$
. Thus, we conclude that the overall terms
$\mbox{IV}_1 + \mbox{IV}_3 + \mbox{IV}_4 + \mbox{IV}_6 = O(m^{-1})$
. Thus, we conclude that the overall terms
![]() $\mbox{IV} = o(1)$
.
$\mbox{IV} = o(1)$
.
Four distinct indices:
![]() $i_1 \ne i_2 \ne l_1 \ne l_2$
. In this case, we can write the summation as
$i_1 \ne i_2 \ne l_1 \ne l_2$
. In this case, we can write the summation as
 \begin{align*} \mbox{V} = \sum_{i_1\ne i_2\ne l_1\ne l_2}^p{b_{i_1l_1}\overline{b}_{i_2l_2}} \cdot \mathbb{E}\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{l_1}^{(k)},k} - \sigma_{i_1l_1}}\big) \big({x_{\pi_{i_2}^{(k)},k}\overline{x}_{\pi_{l_2}^{(k)},k} - \sigma_{i_2l_2}}\big). \end{align*}
\begin{align*} \mbox{V} = \sum_{i_1\ne i_2\ne l_1\ne l_2}^p{b_{i_1l_1}\overline{b}_{i_2l_2}} \cdot \mathbb{E}\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{l_1}^{(k)},k} - \sigma_{i_1l_1}}\big) \big({x_{\pi_{i_2}^{(k)},k}\overline{x}_{\pi_{l_2}^{(k)},k} - \sigma_{i_2l_2}}\big). \end{align*}
For
![]() $i_1 \ne i_2 \ne l_1 \ne l_2$
, we write
$i_1 \ne i_2 \ne l_1 \ne l_2$
, we write
 \begin{align*} \mathbb E\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{l_1}^{(k)},k} - \sigma_{i_1l_1}}\big) \big({x_{\pi_{i_2}^{(k)},k}\overline{x}_{\pi_{l_2}^{(k)},k} - \sigma_{i_2l_2}}\big) & = \mathbb E\overline{x}_{\pi_{i1}^{(k)},k}x_{\pi_{i_2}^{(k)},k}x_{\pi_{l_1}^{(k)},k}\overline{x}_{\pi_{l_2}^{(k)},k} - \frac{1}{{m^2(m - 1)^2}} \\[5pt] & = \frac{{\mathbb E\sum_{i_1\ne i_2\ne l_1\ne l_2}^m{\overline{x}_{i_1k}x_{l_1k}x_{l_2k}\overline{x}_{i_2k}}}} {{m(m - 1)(m - 2)(m - 3)}} \\[5pt] &\quad - \frac{1}{{m^2(m - 1)^2}} = O(m^{-4}). \end{align*}
\begin{align*} \mathbb E\big({\overline{x}_{\pi_{i_1}^{(k)},k}x_{\pi_{l_1}^{(k)},k} - \sigma_{i_1l_1}}\big) \big({x_{\pi_{i_2}^{(k)},k}\overline{x}_{\pi_{l_2}^{(k)},k} - \sigma_{i_2l_2}}\big) & = \mathbb E\overline{x}_{\pi_{i1}^{(k)},k}x_{\pi_{i_2}^{(k)},k}x_{\pi_{l_1}^{(k)},k}\overline{x}_{\pi_{l_2}^{(k)},k} - \frac{1}{{m^2(m - 1)^2}} \\[5pt] & = \frac{{\mathbb E\sum_{i_1\ne i_2\ne l_1\ne l_2}^m{\overline{x}_{i_1k}x_{l_1k}x_{l_2k}\overline{x}_{i_2k}}}} {{m(m - 1)(m - 2)(m - 3)}} \\[5pt] &\quad - \frac{1}{{m^2(m - 1)^2}} = O(m^{-4}). \end{align*}
Note that
 \begin{align*} & \sum_{i_1\neq i_2\neq l_1\neq l_2}b_{i_1l_1}\bar b_{i_2l_2}\\[5pt] & = \Bigg[\sum_{\{i_1,l_1,i_2,l_2\}} - \sum_{\{i_1=i_2\}} - \sum_{\{i_1=l_1\}} - \sum_{\{i_1=l_2\}} - \sum_{\{l_1=i_2\}} - \sum_{\{l_1=l_2\}} - \sum_{\{i_2=l_2\}} + \sum_{\{i_1=i_2=l_1\}} + \sum_{\{i_1=i_2=l_2\}} \\[5pt] & \quad + \sum_{\{i_2=l_1=l_2\}} + \sum_{\{i_1=l_1=l_2\}} + \sum_{\{i_1=i_2,l_1=l_2\}} + \sum_{\{i_1=l_1, i_2=l_2\}} + \sum_{\{i_1=l_2, i_2=l_1\}} - \sum_{\{i_1=i_2=l_1=l_2\}}\Bigg](b_{i_1l_1}\overline{b}_{i_2l_2}) \\[5pt] & = (\textbf{1}^{*}\textbf{B}\textbf{1})(\textbf{1}^{*}\overline{\textbf{B}}\textbf{1}) - \operatorname{tr}\textbf{B} \cdot \textbf{1}^{*}\overline{\textbf{B}}\textbf{1} - \operatorname{tr}\overline{\textbf{B}} \cdot \textbf{1}^{*}\textbf{B}\textbf{1} - 2\textbf{1}^{*}\textbf{B}\overline{\textbf{B}}\textbf 1 - 2\textbf{1}^{*}\textbf{B}\textbf{B}^{*}\textbf{1} + \\[5pt] & \quad 2{\mathrm{Re}}(\textbf{1}^{*}\textbf{B}_\mathrm{d}\textbf{B}^*\textbf 1) + 2{\mathrm{Re}}(\textbf{1}^{*}\textbf{B}\overline{\textbf{B}}_\mathrm{d}\textbf{1}) + \vert\operatorname{tr}\textbf{B}\vert^2 + \operatorname{tr}\textbf{BB}^* + \operatorname{tr}\textbf{B}\overline{\textbf{B}} - \sum_{i=1}^m\vert b_{ii}\vert^2 \\[5pt] & = O(m^2). \end{align*}
\begin{align*} & \sum_{i_1\neq i_2\neq l_1\neq l_2}b_{i_1l_1}\bar b_{i_2l_2}\\[5pt] & = \Bigg[\sum_{\{i_1,l_1,i_2,l_2\}} - \sum_{\{i_1=i_2\}} - \sum_{\{i_1=l_1\}} - \sum_{\{i_1=l_2\}} - \sum_{\{l_1=i_2\}} - \sum_{\{l_1=l_2\}} - \sum_{\{i_2=l_2\}} + \sum_{\{i_1=i_2=l_1\}} + \sum_{\{i_1=i_2=l_2\}} \\[5pt] & \quad + \sum_{\{i_2=l_1=l_2\}} + \sum_{\{i_1=l_1=l_2\}} + \sum_{\{i_1=i_2,l_1=l_2\}} + \sum_{\{i_1=l_1, i_2=l_2\}} + \sum_{\{i_1=l_2, i_2=l_1\}} - \sum_{\{i_1=i_2=l_1=l_2\}}\Bigg](b_{i_1l_1}\overline{b}_{i_2l_2}) \\[5pt] & = (\textbf{1}^{*}\textbf{B}\textbf{1})(\textbf{1}^{*}\overline{\textbf{B}}\textbf{1}) - \operatorname{tr}\textbf{B} \cdot \textbf{1}^{*}\overline{\textbf{B}}\textbf{1} - \operatorname{tr}\overline{\textbf{B}} \cdot \textbf{1}^{*}\textbf{B}\textbf{1} - 2\textbf{1}^{*}\textbf{B}\overline{\textbf{B}}\textbf 1 - 2\textbf{1}^{*}\textbf{B}\textbf{B}^{*}\textbf{1} + \\[5pt] & \quad 2{\mathrm{Re}}(\textbf{1}^{*}\textbf{B}_\mathrm{d}\textbf{B}^*\textbf 1) + 2{\mathrm{Re}}(\textbf{1}^{*}\textbf{B}\overline{\textbf{B}}_\mathrm{d}\textbf{1}) + \vert\operatorname{tr}\textbf{B}\vert^2 + \operatorname{tr}\textbf{BB}^* + \operatorname{tr}\textbf{B}\overline{\textbf{B}} - \sum_{i=1}^m\vert b_{ii}\vert^2 \\[5pt] & = O(m^2). \end{align*}
Here we used the results established in the previous calculation of the four cases. Now, it is easy to see that the summation term of the
![]() $b_{i l}$
part is at most of the order of
$b_{i l}$
part is at most of the order of
![]() $m^2$
. However, the expectation terms are of the order of
$m^2$
. However, the expectation terms are of the order of
![]() $m^{-4}$
, since
$m^{-4}$
, since
![]() $\sum_{i=1}^m{\mathbb{E}\vert x_{ik}\vert^4} \to 0$
$\sum_{i=1}^m{\mathbb{E}\vert x_{ik}\vert^4} \to 0$
![]() $(k=1, \ldots, n)$
. Hence, the term
$(k=1, \ldots, n)$
. Hence, the term
![]() $\mbox{V} = o(1)$
.
$\mbox{V} = o(1)$
.
Putting together the results from the five cases, we obtain the desired result:
Acknowledgements
We thank the Editor, Associate Editor, and the two referees for their insightful comments. Jianghao Li wishes to thank Ms. Xinlei Li for her encouragement and discussion.
Funding information
Zhidong Bai was partially supported by NSFC Grants Nos. 12171198, 12271536 and Team Project of Jilin Provincial Department of Science and Technology No. 20210101147JC. Jiang Hu was partially supported by NSFC Grants Nos. 12292980, 12292982, 12171078, 12326606, National Key R&D Program of China No. 2020YFA0714102, and Fundamental Research Funds for the Central Universities No. 2412023YQ003.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.