Hostname: page-component-76fb5796d-zzh7m Total loading time: 0 Render date: 2024-04-27T00:34:25.943Z Has data issue: false hasContentIssue false
  • English
  • Français

Extreme values, range and weak convergence of integrals of Markov chains

Published online by Cambridge University Press:  14 July 2016

P. J. Brockwell ,
S. I. Resnick  and
N. Pacheco-Santiago
P. J. Brockwell*
Affiliation:
Colorado State University
S. I. Resnick*
Affiliation:
Colorado State University
N. Pacheco-Santiago*
Affiliation:
USAF Academy
*
∗ Postal address: Department of Statistics, Colorado State University, Fort Collins, CO 80523, U.S.A.
∗ Postal address: Department of Statistics, Colorado State University, Fort Collins, CO 80523, U.S.A.
∗∗ Postal address: Qtrs 4510 C, USAF Academy, CO 80840, U.S.A. Research supported by the United States Air Force.
Get access Rights & Permissions [Opens in a new window]

Abstract

A study is made of the maximum, minimum and range on [0, t] of the integral process 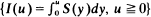where S is a finite state-space Markov chain. Approximate results are derived by establishing weak convergence of a sequence of such processes to a Wiener process. For a particular family of two-state stationary Markov chains we show that the corresponding centered integral processes exhibit the Hurst phenomenon to a remarkable degree in their pre-asymptotic behaviour.

Keywords

STORAGE THEORYDEPENDENT INPUTSINTEGRAL OF A MARKOV CHAINEXTREME VALUESRANGEWEAK CONVERGENCEWIENER PROCESSHURST PHENOMENON
Type
Research Papers
Information
Journal of Applied Probability , Volume 19 , Issue 2 , June 1982 , pp. 272 - 288
Copyright
Copyright © Applied Probability Trust 1982 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported by NSF Grant No. MCS 78–00915–01.

References

Abramowitz, M. and Stegun, I. (1965) Handbook of Mathematical Functions. Dover, New York.Google Scholar
Ali Khan, M. and Gani, J. (1968) Infinite dams with inputs forming a Markov chain. J. Appl. Prob. 5, 72–83.CrossRefGoogle Scholar
Bather, J. A. (1968) A diffusion model for the control of a dam. J. Appl. Prob. 5, 55–71.Google Scholar
Bhattacharya, P. K. and Brockwell, P. J. (1976) The minimum of an additive process with applications to signal estimation and storage theory. Z. Wahrscheinlichkeitsth. 37, 51–75.Google Scholar
Billingsley, P. (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
Brockwell, P. J. (1972) A storage model in which the net growth-rate is a Markov chain. J. Appl. Prob. 9, 129–139.Google Scholar
Brockwell, P. J. (1973) On the spectrum of a class of matrices arising in storage theory. Z. Wahrscheinlichkeitsth. 25, 253–260.Google Scholar
Brockwell, P. J. (1977) Stationary distributions for dams with additive input and content-dependent release rate. Adv. Appl. Prob. 9, 645–663.Google Scholar
Brockwell, P. J. and Pacheco-Santiago, N. (1980) Invariant imbedding and dams with Markovian input rate. J. Appl. Prob. 17, 778–789.Google Scholar
Chung, K. L. (1967) Markov Chains with Stationary Transition Probabilities, 2nd edn. Springer-Verlag, Berlin.Google Scholar
Çinlar, E. and Pinsky, M. (1971) A stochastic integral in storage theory. Z. Wahrscheinlichkeitsth. 2, 180–224.Google Scholar
Doetsch, G. (1974) Introduction to the Theory and Application of the Laplace Transformation. Springer-Verlag, Berlin.Google Scholar
Erickson, R. V. (1972) Stationary measures for a class of storage models driven by a Markov chain. Ann. Math. Statist. 43, 997–1007.Google Scholar
Faddy, M. J. (1974) Optimal control of finite dams: discrete (2-stage) output procedure. J. Appl. Prob. 11, 111–121.Google Scholar
Feller, W. (1951) The asymptotic distribution of the range of sums of independent random variables. Ann. Math. Statist. 22, 427–432.Google Scholar
Fukushima, M. and Hitsuda, M. (1967) On a class of Markov processes taking values on lines and the central limit theorem. Nagoya Math. J. 30, 47–56.Google Scholar
Gani, J. and Prabhu, N. U. (1960) The content of a dam as the supremum of an infinitely divisible process. J. Math. Mech. 9, 639–651.Google Scholar
Harrison, J. M. and Resnick, S. I. (1975) The stationary distribution and first-exit probabilities of a storage process with general release rate. Math. Operat. Res. 1, 347–358.Google Scholar
Hurst, H. (1951) Long-term storage capacity of reservoirs. Trans. Amer. Soc. Civil Engrs. 116, 778–808.Google Scholar
Iglehart, D. and Whitt, W. (1971) The equivalence of functional central limit theorems for counting processes and associated partial sums. Ann. Math. Statist. 42, 1372–1378.Google Scholar
Kendall, D. G. (1957) Some problems in the theory of dams. J. R. Statist. Soc. B 19, 207–212.Google Scholar
Lindvall, T. (1973) Weak convergence on the function space D[0, 8). J. Appl. Prob. 10, 109–121.Google Scholar
Mcneil, D. R. (1972) A simple model for a dam in continuous time with Markovian input. Z. Wahrscheinlichkeitsth. 21, 241–254.CrossRefGoogle Scholar
Moran, P. A. P. (1959) The Theory of Storage. Methuen, London.Google Scholar
Odoom, S. and Lloyd, E. (1965) A note on the equilibrium distribution of levels in a semi-infinite reservoir subject to Markovian inputs and unit withdrawals. J. Appl. Prob. 1, 215–222.CrossRefGoogle Scholar
Pakes, A. G. (1973) On dams with Markovian inputs. J. Appl. Prob. 10, 317–329.Google Scholar
Pinsky, M. (1968) Differential equations with a small parameter and the central limit theorem for functions defined on a Markov chain. Z. Wahrscheinlichkeitsth. 9, 101–111.CrossRefGoogle Scholar
Salas, J. D., Boes, D. C., Yevjevich, V. and Pegram, G. G. S. (1979) Hurst phenomenon as a preasymptotic behavior. J. Hydrology 44, 1–15.Google Scholar
Vervaat, W. (1972) Functional central limit theorems for process with positive drift and their inverses. Z. Wahrscheinlichkeitsth. 23, 245–253.CrossRefGoogle Scholar
Whitt, W. (1980) Some useful functions for functional limit theorems. Math. Operat. Res. 5, 67–85.Google Scholar
Zuckerman, D. (1977) Two-stage output procedure of a finite dam. J. Appl. Prob. 14, 421–425.Google Scholar