Hostname: page-component-848d4c4894-xm8r8 Total loading time: 0 Render date: 2024-06-24T21:28:00.894Z Has data issue: false hasContentIssue false
  • English
  • Français

Estimation of the variance for the multitype Galton–Watson process

Published online by Cambridge University Press:  14 July 2016

K. Nanthi
K. Nanthi*
Affiliation:
University of Madras
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is concerned with the estimation of the variance for the multitype Galton-Watson process X = {Xn = (Xn(1),…, Xn(p)); n ≧ 0}. Two estimators for the variance matrix are obtained and asymptotic results for the estimators are given. The first is a maximum likelihood estimator based upon knowledge of individual offspring sizes, the second estimator is based on parent-offspring type combination counts only. Estimators for the asymptotic variances of the Asmussen and Keiding estimator 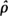and Becker estimator 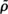are also proposed.

Keywords

CONFIDENCE BOUNDSASYMPTOTIC PROPERTIES
Type
Short Communications
Information
Journal of Applied Probability , Volume 19 , Issue 2 , June 1982 , pp. 408 - 414
Copyright
Copyright © Applied Probability Trust 1982 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work forms part of the authors' doctoral dissertation under the guidance of Professor K. N. Venkataraman, University of Madras. Research supported by the University Grants Commission, India.

References

Asmussen, S. and Keiding, N. (1978) Martingale central limit theorems and asymptotic estimation theory for multitype branching processes. Adv. Appl. Prob. 10, 109–129.CrossRefGoogle Scholar
Athreya, K. B. and Ney, P. E. (1972) Branching Processes. Springer-Verlag, Berlin.CrossRefGoogle Scholar
Becker, N. (1977) Estimation for discrete time branching processes with application to epidemics. Biometrics 33, 515–522.CrossRefGoogle ScholarPubMed
Billingsley, P. (1961) Statistical Inference for Markov Processes. The University of Chicago Press, Chicago.Google Scholar
Billingsley, P. (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
Dion, J. P. (1975) Estimation of the variance of a branching process. Ann. Statist. 3, 1183–1187.CrossRefGoogle Scholar
Dion, J. P. and Keiding, N. (1978) In Advances in Probability, ed. Ney, P., Dekker, New York.Google Scholar
Heyde, C. C. (1974) On estimating the variance of the offspring distribution in a simple branching process. Adv. Appl. Prob. 6, 421–433.CrossRefGoogle Scholar
Keiding, N. and Lauritzen, S. L. (1978) Marginal maximum likelihood estimates and estimation of the offspring mean in a branching process. Scand. J. Statist. 5, 106–110.Google Scholar
Kesten, H. and Stigum, B. P. (1966) A limit theorem for multidimensional Galton-Watson processes. Ann. Math. Statist. 37, 1211–1223.CrossRefGoogle Scholar
Loève, M. (1968) Probability Theory. Affiliated East-West Press Pvt. Ltd., New Delhi.Google Scholar
Nanthi, K. (1978) Estimation of the offspring mean/growth rate in a supercritical Galton-Watson process/multitype Galton-Watson process. Madras Univ. J. B, 41.Google Scholar