Hostname: page-component-77c89778f8-cnmwb Total loading time: 0 Render date: 2024-07-17T00:46:33.858Z Has data issue: false hasContentIssue false
  • English
  • Français

Equality of critical densities in continuum percolation

Part of: Equilibrium statistical mechanics Stochastic processes Special processes

Published online by Cambridge University Press:  14 July 2016

Ronald Meester
Ronald Meester*
Affiliation:
University of Utrecht
*
∗Postal address: Department of Mathematics, University of Utrecht, P.O. Box 80.010, 3508 TA Utrecht, The Netherlands.
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider a homogeneous Poisson process in 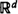with density ρ, and add the origin as an extra point. Now connect any two points x and y of the process with probability g(x − y), independently of the point process and all other pairs, where g is a function which depends only on the Euclidean distance between x and y, and which is nonincreasing in the distance. We distinguish two critical densities in this model. The first is the infimum of all densities for which the cluster of the origin is infinite with positive probability, and the second is the infimum of all densities for which the expected size of the cluster of the origin is infinite. It is known that if 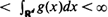, then the two critical densities are non-trivial, i.e. bounded away from 0 and ∞. It is also known that if g is of the form 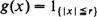, for some r > 0, then the two critical densities coincide. In this paper we generalize this result and show that under the integrability condition mentioned above the two critical densities are always equal.

Keywords

POISSON PROCESSPERCOLATION THEORY

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Secondary: 82B43: Percolation 60G55: Point processes
Type
Research Papers
Information
Journal of Applied Probability , Volume 32 , Issue 1 , March 1995 , pp. 90 - 104
Copyright
Copyright © Applied Probability Trust 1995 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aizenman, M. and Barsky, D. J. (1987) Sharpness of the phase transition in percolation models. Commun. Math. Phys. 108, 489–526.CrossRefGoogle Scholar
Berg, J. V.D. and Kesten, H. (1985) Inequalities with applications to percolation and reliability. J. Appl. Prob. 22, 556–569.CrossRefGoogle Scholar
Grimmett, G. (1989) Percolation. Springer-Verlag, New York.Google Scholar
Hall, P. (1985) On continuum percolation. Ann. Prob. 13, 1250–1266.CrossRefGoogle Scholar
Kesten, H. (1980) The critical probability of bond percolation on the square lattice equals ½. Commun. Math. Phys. 74, 41–59.CrossRefGoogle Scholar
Kesten, H. (1982) Percolation Theory for Mathematicians. Birkhäuser, Boston.Google Scholar
Menshikov, M. V. (1986) Coincidence of critical points in percolation problems. Sov. Math. Dokl. 33, 856–859.Google Scholar
Menshikov, M. V. and Sidorenko, A. F. (1987) Coincidence of critical points for Poisson percolation models. Theory Prob. Appl. 32, 603–606.Google Scholar
Menshikov, M. V., Molchanov, S. and Sidorenko, A. F. (1986) Percolation theory and some applications. Itogi Nauki i Techniki. Series on probability theory, Math. Stat. Theoret. Cybernet. 24, 53–110.Google Scholar
Penrose, M. D. (1991) On a continuum percolation model. Adv. Appl. Prob. 23, 536–556.CrossRefGoogle Scholar
Roy, R. (1990) The Russo-Seymour-Welsh theorem and the equality of critical densities and the ‘dual’ densities for continuum percolation on ½. Ann. Prob. 18, 1563–1575.CrossRefGoogle Scholar
Roy, R. (1991) Percolation of Poisson sticks in the plane. Prob. Theory Rel. Fields 89, 503–517.Google Scholar
Zuev, S. A. and Sidorenko, A. F. (1985a) Continuous models of percolation theory I. Theoret. Math. Phys. 62, 77–86 (51-59 in translation).Google Scholar
Zuev, S. A. and Sidorenko, A. F. (1985b) Continuous models of percolation theory II, Theoret. Math. Phys. 62, 253–262.Google Scholar