Hostname: page-component-76fb5796d-9pm4c Total loading time: 0 Render date: 2024-04-25T07:55:30.938Z Has data issue: false hasContentIssue false
  • English
  • Français

A central limit theorem for conservative fragmentation chains

Part of: Limit theorems Markov processes

Published online by Cambridge University Press:  17 March 2023

Sylvain Rubenthaler Open the ORCID record for Sylvain Rubenthaler [Opens in a new window]
Sylvain Rubenthaler*
Affiliation:
Université Côte d’Azur
*
*Postal address: Université Côte d’Azur, CNRS, LJAD, France. Email: rubentha@unice.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

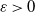We are interested in a fragmentation process. We observe fragments frozen when their sizes are less than $\varepsilon$ ($\varepsilon>0$). It is known (Bertoin and Martínez, 2005) that the empirical measure of these fragments converges in law, under some renormalization. Hoffmann and Krell (2011) showed a bound for the rate of convergence. Here, we show a central limit theorem, under some assumptions. This gives us an exact rate of convergence.

Keywords

Fragmentationbranching processrenewal theorycentral-limit theoremspropagation of chaosU-statistics

MSC classification

Primary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.)
Secondary: 60F05: Central limit and other weak theorems
Type
Original Article
Information
Journal of Applied Probability , Volume 60 , Issue 3 , September 2023 , pp. 1031 - 1068
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asmussen, S. (2003). Applied Probability and Queues, 2nd edn (Appl. Math. (New York) 51). Springer, New York.Google Scholar
Bertoin, J. (2002). Self-similar fragmentations. Ann. Inst. H. Poincaré Prob. Statist. 38, 319–340.CrossRefGoogle Scholar
Bertoin, J. (2006). Random Fragmentation and Coagulation Processes (Cambridge Studies Adv. Math. 102). Cambridge University Press.Google Scholar
Bertoin, J. and Martínez, S. (2005). Fragmentation energy. Adv. Appl. Prob. 37, 553–570.CrossRefGoogle Scholar
Bond, F. C. (1952). The third theory of comminution. Trans. AIME Mining Eng. 193, 484–494.Google Scholar
Charles, R. J. (1957). Energy–size reduction relationships in comminution. Trans. AIME Mining Eng. 208, 80–88.Google Scholar
Dawson, D. A. and Zheng, X. (1991). Law of large numbers and central limit theorem for unbounded jump mean-field models. Adv. Appl. Math. 12, 293–326.CrossRefGoogle Scholar
de la Peña, V. H. and Giné, E. (1999). Decoupling. Springer, New York.CrossRefGoogle Scholar
Del Moral, P., Patras, F. and Rubenthaler, S. (2009). Tree-based functional expansions for Feynman–Kac particle models. Ann. Appl. Prob. 19, 778–825.CrossRefGoogle Scholar
Del Moral, P., Patras, F. and Rubenthaler, S. (2011). Convergence of U-statistics for interacting particle systems. J. Theor. Prob. 24, 1002–1027.CrossRefGoogle Scholar
Del Moral, P., Patras, F. and Rubenthaler, S. (2011). A mean field theory of nonlinear filtering. In The Oxford Handbook of Nonlinear Filtering. Oxford University Press, pp. 705–740.Google Scholar
Devoto, D. and Martnez, S. (1998). Truncated Pareto law and oresize distribution of ground rocks. Math. Geology 30, 661–673.CrossRefGoogle Scholar
Dynkin, E. B. and Mandelbaum, A. (1983). Symmetric statistics, Poisson point processes, and multiple Wiener integrals. Ann. Statist. 11, 739–745.CrossRefGoogle Scholar
Fontbona, J., Krell, N. and Martnez, S. (2010). Energy efficiency of consecutive fragmentation processes. J. Appl. Prob. 47, 543–561.CrossRefGoogle Scholar
Harris, S. C., Knobloch, R. and Kyprianou, A. E. (2010). Strong law of large numbers for fragmentation processes. Ann. Inst. H. Poincaré Prob. Statist. 46, 119–134.CrossRefGoogle Scholar
Hoffmann, M. and Krell, N. (2011). Statistical analysis of self-similar conservative fragmentation chains. Bernoulli 17, 395–423.CrossRefGoogle Scholar
Lee, A. J. (1990). U-statistics (Statistics: Textbooks and Monographs 110). Marcel Dekker Inc., New York.Google Scholar
Meleard, S. (1998). Convergence of the fluctuations for interacting diffusions with jumps associated with Boltzmann equations. Stoch. Stoch. Rep. 63, 195–225.CrossRefGoogle Scholar
Perrier, E. M. and Bird, N. R. (2002). Modelling soil fragmentation: The pore solid fractal approach. Soil and Tillage Res. 64, 91–99.CrossRefGoogle Scholar
Rubenthaler, S. (2016). Central limit theorem through expansion of the propagation of chaos for Bird and Nanbu systems. Ann. Fac. Sci. Toulouse Math. (6) 25, 829–873.CrossRefGoogle Scholar
Sgibnev, M. S. (2002). Stone’s decomposition of the renewal measure via Banach-algebraic techniques. Proc. Amer. Math. Soc. 130, 2425–2430.CrossRefGoogle Scholar
Turcotte, D. L. (1986). Fractals and fragmentation. J. Geophys. Res. 91, 1921–1926.CrossRefGoogle Scholar
Uchiyama, K. (1988). Fluctuations in a Markovian system of pairwise interacting particles. Prob. Theory Relat. Fields 79, 289–302.CrossRefGoogle Scholar
Walker, W. H., Lewis, W. K., McAdams, W. H. and Gilliland, E. R. (1967). Principles of Chemical Engineering. McGraw-Hill, New York.Google Scholar
Weiss, N. L. (1985). SME Mineral Processing Handbook. Society of Mining Engineers of the American Institute of Mining, Metallurgical, and Petroleum Engineers, New York.Google Scholar