Hostname: page-component-848d4c4894-pjpqr Total loading time: 0 Render date: 2024-06-24T22:30:08.511Z Has data issue: false hasContentIssue false
  • English
  • Français

Branching processes with immigration

Published online by Cambridge University Press:  14 July 2016

A. G. Pakes
A. G. Pakes*
Affiliation:
Monash University
Get access Rights & Permissions [Opens in a new window]

Extract

Consider a branching process in which each individual reproduces independently of all others and has probability aj (j = 0, 1, ···) of giving rise to j progeny in the following generation, and in which there is an independent immigration component where, with probability bj (j = 0, 1, ···) j objects enter the population at each generation. Then letting Xn (n = 0, 1, ···) be the population size of the nth generation, it is known (Heathcote (1965), (1966)) that {Xn} defines a Markov chain on the non-negative integers and it is called a branching process with immigration (b.p.i.). 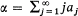We shall call the process sub-critical or super-critical according as the mean number of offspring of an individual, , satisfies α < 1 or α > 1, respectively. Unless stated specifically to the contrary, we assume that the following condition holds.

Type
Research Papers
Information
Journal of Applied Probability , Volume 8 , Issue 1 , March 1971 , pp. 32 - 42
Copyright
Copyright © Applied Probability Trust 1971 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Dwass, M. (1968) A theorem about infinitely divisible distributions. Z. Wahrscheinlichkeitsth. 9, 287–289.Google Scholar
Feller, W. (1968) An Introduction to Probability Theory and its Applications. Vol. 1, 3rd ed. Wiley, New York.Google Scholar
Gnedenko, B. and Kolmogorov, A. (1954) Limit Distributions for Sums of Independent Random Variables. Addison-Wesley, Reading.Google Scholar
Harris, T. E. (1948) Branching processes. Ann. Math. Statist. 19, 474–494.CrossRefGoogle Scholar
Harris, T. E. (1963) The Theory of Branching Processes. Springer-Verlag, Berlin.CrossRefGoogle Scholar
HEATHCOTE, C. R. (1965) A branching process allowing immigration. J. R. Statist. Soc. B 27, 138–143.Google Scholar
Heathcote, C. R. (1966) Corrections and comments on the paper ‘A branching process allowing immigration’. J. R. Statist. Soc. B 28, 213–217.Google Scholar
Heathcote, C. R., Seneta, E. and Vere-Jones, D. (1967) A refinement of two theorems in the theory of branching processes. Teor. Veroyat. Primen. 12, 341–346.Google Scholar
Heyde, C. C. (1970) Extension of a result of Seneta for the super-critical Galton-Watson process. Ann. Math. Statist. 41, 739–742.Google Scholar
Karlin, S. and Mcgregor, J. (1966) Spectral theory of branching processes. I. Z. Wahrscheinlichkeitsth. 5, 6–33.Google Scholar
Kendall, D. G. (1959) Unitary dilations of Markov transition operators and the corresponding integral representations for transition probability matrices. Probability and Statistics, 162–174. Edited by Grenander, U. Wiley, New York.Google Scholar
Kendall, D. G. (1966) On super critical branching processes with a positive chance of extinction. Research Papers in Statistics, 157–165. Edited by David, F. N. Wiley, London.Google Scholar
LoèVe, M. (1963) Probability Theory. Van Nostrand, Princeton.Google Scholar
Révész, P. (1968) The Laws of Large Numbers. Academic Press, New York.Google Scholar
Seneta, E. (1969) Functional equations and the Galton-Watson process. Adv. Appl. Prob. 1, 1–42.Google Scholar
Seneta, E. (1970) On the supercritical Galton-Watson process with immigration. Math. Biosciences 7, 9–14.Google Scholar
Titchmarsh, E. C. (1939) The Theory of Functions. 2nd ed. Oxford University Press.Google Scholar
Vere-Jones, D. (1962) Geometric ergodicity in denumerable Markov chains. Quart. J. Math. 13, 7–28.Google Scholar