Hostname: page-component-77c89778f8-sh8wx Total loading time: 0 Render date: 2024-07-19T22:07:56.875Z Has data issue: false hasContentIssue false
  • English
  • Français

An infinite variance solidarity theorem for Markov renewal functions

Part of: Special processes

Published online by Cambridge University Press:  14 July 2016

M. S. Sgibnev
M. S. Sgibnev*
Affiliation:
Institute of Mathematics, Novosibirsk
*
∗Postal address: Institute of Mathematics, Siberian Branch of the Russian Academy of Sciences, Novosibirsk 90, 630090 Russia.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 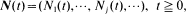, be a recurrent Markov renewal process and Mik(t) be the expected value of Nk(t) provided that at the initial moment the system is in state i. It is shown that when the mean recurrence times μ ii are finite, the differences μ ij Mki (t) – t behave asymptotically the same for all states i and k.

Keywords

MARKOV RENEWAL FUNCTIONSINFINITE VARIANCE

MSC classification

Primary: 60K15: Markov renewal processes, semi-Markov processes
Secondary: 60K05: Renewal theory
Type
Research Papers
Information
Journal of Applied Probability , Volume 33 , Issue 2 , September 1996 , pp. 434 - 438
Copyright
Copyright © Applied Probability Trust 1996 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Çinlar, E. (1969) Markov renewal theory. Adv. Appl Prob. 1, 123–187.Google Scholar
[2] Pyke, R. (1961) Markov renewal processes: definitions and preliminary properties. Ann. Math. Statist. 32, 1231–1242.CrossRefGoogle Scholar
[3] Pyke, R. (1961) Markov renewal processes with finitely many states. Ann. Math. Statist. 32, 1243–1259.Google Scholar
[4] Pyke, R. and Schaufele, R. (1964) Limit theorems for Markov renewal processes. Ann. Math. Statist. 35, 1746–1764.Google Scholar
[5] Sgibnev, M. S. (1981) Renewal theorem in the case of an infinite variance. Siberian Math. J. 22, 787–796.Google Scholar
[6] Teugels, J. L. (1968) Renewal theorems when the first or the second moment is infinite. Ann. Math. Statist. 39, 1210–1219.CrossRefGoogle Scholar
[7] Teugels, J. L. (1968) Exponential ergodicity in Markov renewal processes. J. Appl. Prob. 5, 387–400.CrossRefGoogle Scholar
[8] Teugels, J. L. (1970) Regular variation of Markov renewal functions. J. London Math. Soc. 2, 179–190.Google Scholar