Hostname: page-component-848d4c4894-ndmmz Total loading time: 0 Render date: 2024-05-12T13:19:31.160Z Has data issue: false hasContentIssue false
  • English
  • Français

Almost sure stability of maxima

Published online by Cambridge University Press:  14 July 2016

Sidney I. Resnick  and
R. J. Tomkins
Sidney I. Resnick*
Affiliation:
Technion — Israel Institute of Technology
R. J. Tomkins
Affiliation:
University of Saskatchewan, Regina
*
*Now at Stanford University.
Get access Rights & Permissions [Opens in a new window]

Abstract

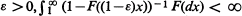For random variables {Xn, n ≧ 1} unbounded above set Mn = max {X1, X2, …, Xn}. When do normalizing constants bn exist such that Mn/bn→ 1 a.s.; i.e., when is {Mn} a.s. stable? If {Xn} is i.i.d. then {Mn} is a.s. stable iff for all and in this case bn ∼ F–1 (1 – 1/n) Necessary and sufficient conditions for lim supn→∞, Mn/bn = l > 1 a.s. are given and this is shown to be insufficient in general for lim infn→∞Mn/bn = 1 a.s. except when l = 1. When the Xn are r.v.'s defined on a finite Markov chain, one shows by means of an analogue of the Borel Zero-One Law and properties of semi-Markov matrices that the stability problem for this case can be reduced to the i.i.d. case.

Keywords

MAXIMA; ALMOST SURE STABILITYSEMI-MARKOV PROCESSESMARKOV CHAINS
Type
Research Papers
Information
Journal of Applied Probability , Volume 10 , Issue 2 , June 1973 , pp. 387 - 401
Copyright
Copyright © Applied Probability Trust 1973 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Barndorff-Nielsen, O. (1961) On the rate of growth of the partial maxima of a sequence of independent identically distributed random variables. Math. Scand. 9, 383–394.Google Scholar
[2] Barndorff-Nielsen, O. (1963) On the limit behavior of extreme order statistics. Ann. Math. Statist. 34, 992–1002.Google Scholar
[3] Chung, K. L. (1960) Markov Chains with Stationary Transition Probabilities. Springer-Verlag, Berlin.Google Scholar
[4] Geffroy, J. (1958) Contributions à. la théorie des valeurs extrèmes. Publ. Inst. Statist. Paris 7, 37–123.Google Scholar
[5] Gnedenko, B. V. (1943) Sur la distribution limite du terme maximum d'une séries aléatoire. Ann. Math. 44, 423–453.Google Scholar
[6] Haan, L. De and Hordijk, A. (1972) The rate of growth of sample maxima. Ann. Math. Statist. 43, 1185–1196.Google Scholar
[7] Pickands, J. (1967) Sample sequences of maxima. Ann. Math. Statist. 38, 1570–1574.Google Scholar
[8] Resnick, S. I. and Neuts, M. F. (1970) Limit laws for maxima of a sequence of random variables defined on a Markov chain. Adv. Appl. Prob. 2, 323–343.CrossRefGoogle Scholar
[9] Resnick, S. I. (1971) Tail equivalence and its applications. J. Appl. Prob. 8, 136–156.Google Scholar
[10] Resnick, S. I. (1971) Asymptotic location and recurrence properties of maxima of a sequence of random variables defined on a Markov chain. Zeit. Wahrscheinlichkeitsth. 18, 197–217.Google Scholar
[11] Resnick, S. I. (1972) Stability of maxima of random variables defined on a Markov chain. Adv. Appl. Prob. 4, 285–295.CrossRefGoogle Scholar