Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-25T07:52:14.570Z Has data issue: false hasContentIssue false
  • English
  • Français

Subgeometric ergodicity and β-mixing

Part of: Ergodic theory Markov processes

Published online by Cambridge University Press:  16 September 2021

Mika Meitz Open the ORCID record for Mika Meitz [Opens in a new window]  and
Pentti Saikkonen
Pentti Saikkonen*
Affiliation:
University of Helsinki
*
**Postal address: Department of Mathematics and Statistics, University of Helsinki, PO Box 68, FI–00014 University of Helsinki, Finland. Email address: pentti.saikkonen@helsinki.fi
Get access Rights & Permissions [Opens in a new window]

Abstract

It is well known that stationary geometrically ergodic Markov chains are 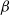$\beta$ -mixing (absolutely regular) with geometrically decaying mixing coefficients. Furthermore, for initial distributions other than the stationary one, geometric ergodicity implies $\beta$ -mixing under suitable moment assumptions. In this note we show that similar results hold also for subgeometrically ergodic Markov chains. In particular, for both stationary and other initial distributions, subgeometric ergodicity implies $\beta$ -mixing with subgeometrically decaying mixing coefficients. Although this result is simple, it should prove very useful in obtaining rates of mixing in situations where geometric ergodicity cannot be established. 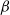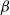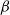To illustrate our results we derive new subgeometric ergodicity and $\beta$ -mixing results for the self-exciting threshold autoregressive model.

Keywords

Markov chainrate of convergencemixing coefficientsubgeometric ratesubexponential ratepolynomial rateSETAR model

MSC classification

Primary: 60J05: Discrete-time Markov processes on general state spaces
Secondary: 37A25: Ergodicity, mixing, rates of mixing
Type
Original Article
Information
Journal of Applied Probability , Volume 58 , Issue 3 , September 2021 , pp. 594 - 608
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The supplementary material for this article can be found at http://doi.org/10.1017/jpr.2020.108.

References

Bradley, R. C. (1986). Basic properties of strong mixing conditions. In Dependence in Probability and Statistics, eds E. Eberlein and M. S. Taqqu, pp. 165–192. BirkhÄuser, Boston.CrossRefGoogle Scholar
Bradley, R. C. (2005). Basic properties of strong mixing conditions: a survey and some open questions. Prob. Surveys 2, 107–144.CrossRefGoogle Scholar
Bradley, R. C. (2007). Introduction to Strong Mixing Conditions, Vols 1–3. Kendrick Press, Heber City.Google Scholar
Chan, K. S., Petruccelli, J. D., Tong, H. and Woolford, S. W. (1985). A multiple-threshold AR(1) model. J. Appl. Prob. 22, 267–279.CrossRefGoogle Scholar
Davydov, Y. A. (1973). Mixing conditions for Markov chains. Theory Prob. Appl. 18, 312–328.CrossRefGoogle Scholar
Douc, R., Fort, G., Moulines, E. and Soulier, P. (2004). Practical drift conditions for subgeometric rates of convergence. Ann. Appl. Prob. 14, 1353–1377.CrossRefGoogle Scholar
Douc, R., Moulines, E., Priouret, P. and Soulier, P. (2018). Markov Chains. Springer, Cham.CrossRefGoogle Scholar
Doukhan, P. (1994). Mixing: Properties and Examples. Springer, New York.CrossRefGoogle Scholar
Fort, G. and Moulines, E. (2000). V-subgeometric ergodicity for a Hastings–Metropolis algorithm. Statist. Prob. Lett. 49, 401–410.CrossRefGoogle Scholar
Fort, G. and Moulines, E. (2003). Polynomial ergodicity of Markov transition kernels. Stoch. Proc. Appl. 103, 57–99.CrossRefGoogle Scholar
Jarner, S. F. and Roberts, G. O. (2002). Polynomial convergence rates of Markov chains. Ann. Appl. Prob. 12, 224–247.CrossRefGoogle Scholar
Jarner, S. F. and Tweedie, R. L. (2003). Necessary conditions for geometric and polynomial ergodicity of random-walk-type Markov chains. Bernoulli 9, 559–578.CrossRefGoogle Scholar
Klokov, S. A. (2007). Lower bounds of mixing rate for a class of Markov processes. Theory Prob. Appl. 51, 528–535.CrossRefGoogle Scholar
Klokov, S. A. and Veretennikov, A. Y. (2004). Sub-exponential mixing rate for a class of Markov chains. Math. Commun. 9, 9–26.Google Scholar
Klokov, S. A. and Veretennikov, A. Y. (2005). On subexponential mixing rate for Markov processes. Theory Prob. Appl. 49, 110–122.CrossRefGoogle Scholar
Liebscher, E. (2005). Towards a unified approach for proving geometric ergodicity and mixing properties of nonlinear autoregressive processes. J. Time Series Anal. 26, 669–689.CrossRefGoogle Scholar
Meitz, M. and Saikkonen, P. (2020). Subgeometrically ergodic autoregressions. To appear in Econometric Theory. Available at http://doi.org/10.1017/S0266466620000419.CrossRefGoogle Scholar
Meitz, M. and Saikkonen, P. (2021). Subgeometric ergodicity and $\beta$ -mixing: supplementary material. Available at http://doi.org/10.1017/[TO BE SET].Google Scholar
Meyn, S. P. and Tweedie, R. L. (2009). Markov Chains and Stochastic Stability, 2nd edn. Cambridge University Press.CrossRefGoogle Scholar
Nummelin, E. and Tuominen, P. (1982). Geometric ergodicity of Harris recurrent Markov chains with applications to renewal theory. Stoch. Proc. Appl. 12, 187–202.CrossRefGoogle Scholar
Nummelin, E. and Tuominen, P. (1983). The rate of convergence in Orey’s theorem for Harris recurrent Markov chains with applications to renewal theory. Stoch. Proc. Appl. 15, 295–311.CrossRefGoogle Scholar
Stone, C. and Wainger, S. (1967). One-sided error estimates in renewal theory. J. Anal. Math. 20, 325–352.CrossRefGoogle Scholar
Tuominen, P. and Tweedie, R. L. (1994). Subgeometric rates of convergence of f-ergodic Markov chains. Adv. Appl. Prob. 26, 775–798.CrossRefGoogle Scholar
Tweedie, R. L. (1983). Criteria for rates of convergence of Markov chains, with application to queueing and storage theory. In Probability, Statistics and Analysis, eds J. F. C. Kingman and G. E. H. Reuter, pp. 260–276. Cambridge University Press.CrossRefGoogle Scholar
Veretennikov, A. Y. (1988). Bounds for the mixing rate in the theory of stochastic equations. Theory Prob. Appl. 32, 273–281.CrossRefGoogle Scholar
Veretennikov, A. Y. (1991). Estimating the mixing rate for Markov processes. Lith. Math. J. 31, 27–34.CrossRefGoogle Scholar
Veretennikov, A. Y. (2000). On polynomial mixing and convergence rate for stochastic difference and differential equations. Theory Prob. Appl. 44, 361–374.CrossRefGoogle Scholar
Veretennikov, A. Y. and Gulinskii, O. V. (1990). Rate of mixing and the averaging principle for stochastic recursive procedures. Autom. Remote Control 51, 779–788.Google Scholar
Volkonskii, V. A. and Rozanov, Y. A. (1959). Some limit theorems for random functions, I. Theory Prob. Appl. 4, 178–197.CrossRefGoogle Scholar
Volkonskii, V. A. and Rozanov, Y. A. (1961). Some limit theorems for random functions, II. Theory Prob. Appl. 6, 186–198.CrossRefGoogle Scholar
Supplementary material: PDF

Meitz and Saikkonen supplementary material

Meitz and Saikkonen supplementary material

Download Meitz and Saikkonen supplementary material(PDF)
PDF 242 KB