Hostname: page-component-84b7d79bbc-c654p Total loading time: 0 Render date: 2024-07-26T20:05:31.943Z Has data issue: false hasContentIssue false
  • English
  • Français

On sequential occupancy problems

Published online by Cambridge University Press:  14 July 2016

Lars Holst
Lars Holst*
Affiliation:
Uppsala University
*
∗Postal address: Department of Mathematics, Thunbergsv. 3, S-75238 Uppsala, Sweden.
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider n cells into which balls are thrown at random until k cells contain at least l + 1 balls each. Let Yl, · ··, Yn be the number of balls in the cells when stopping. In this paper two representations are given for the characteristic functions of random variables of the form 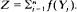The usefulness of these representations are illustrated by two examples. In the first the number of cells with exactly one ball when each cell contains at least one ball is considered. In the second the waiting time until the ball-throwing process stops is discussed.

Keywords

BIRTHDAY PROBLEMSCOUPON-COLLECTINGOCCUPANCYSEQUENTIAL OCCUPANCYURN MODELSPOISSON PROCESSWAITING TIMELIMIT THEOREMS
Type
Research Papers
Information
Journal of Applied Probability , Volume 18 , Issue 2 , June 1981 , pp. 435 - 442
Copyright
Copyright © Applied Probability Trust 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported by a fellowship from the American-Scandinavian Foundation and a grant from the Swedish Natural Science Research Council. The work was partly carried out while the author was visiting Stanford University.

References

Andersson, K., Sobel, M. and Uppuluri, V. R. R. (1980) Multivariate hypergeometric and multinomial waiting times. Technical Report No. 147, Department of Statistics, Stanford.Google Scholar
Baum, L. E. and Billingsley, P. (1965) Asymptotic distribution for the coupon collector's problem. Ann. Math. Statist. 36, 1835–1839.Google Scholar
Bekessy, A. (1964) On classical occupancy problems II (sequential occupancy). Magy. Tud. Akad. Mat. Kutató Int. Közl. 9, 133–141.Google Scholar
Erdös, P. and Renyi, A. (1961) On a classical problem of probability theory. Magy. Tud. Akad. Mat. Kutató Int. Közl. 6, 215–220.Google Scholar
Holst, L. (1979) A unified approach to limit theorems for urn models. J. Appl. Prob. 16, 154–162.Google Scholar
Johnson, N. L. and Kotz, S. (1977) Urn Models and their Applications: An Approach to Modern Discrete Probability Theory. Wiley, New York.Google Scholar
Rao, C. R. (1973) Linear Statistical Inference and its Applications, 2nd edition. Wiley, New York.Google Scholar
Samuel-Cahn, E. (1974) Asymptotic distributions for occupancy and waiting time problems with positive probability of falling through the cells. Ann. Prob. 2, 515–521.Google Scholar