Hostname: page-component-77c89778f8-sh8wx Total loading time: 0 Render date: 2024-07-16T19:26:53.776Z Has data issue: false hasContentIssue false
  • English
  • Français

Gaussian process approximations for multicolor Pólya urn models

Part of: Limit theorems Physiological, cellular and medical topics

Published online by Cambridge University Press:  25 February 2021

Konstantin Borovkov Open the ORCID record for Konstantin Borovkov [Opens in a new window]
Konstantin Borovkov*
Affiliation:
The University of Melbourne
*
*Postal address: School of Mathematics and Statistics, The University of Melbourne, Parkville3010, Australia. Email address: borovkov@unimelb.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

Motivated by mathematical tissue growth modelling, we consider the problem of approximating the dynamics of multicolor Pólya urn processes that start with large numbers of balls of different colors and run for a long time. Using strong approximation theorems for empirical and quantile processes, we establish Gaussian process approximations for the Pólya urn processes. The approximating processes are sums of a multivariate Brownian motion process and an independent linear drift with a random Gaussian coefficient. The dominating term between the two depends on the ratio of the number of time steps n to the initial number of balls N in the urn. We also establish an upper bound of the form 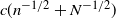$c(n^{-1/2}+N^{-1/2})$ for the maximum deviation over the class of convex Borel sets of the step-n urn composition distribution from the approximating normal law.

Keywords

multicolor Pólya–Eggenberger urnstrong approximationKiefer processproliferative tissue growthcentral limit theoremconvergence rates

MSC classification

Primary: 60F17: Functional limit theorems; invariance principles
Secondary: 60F15: Strong theorems 60F05: Central limit and other weak theorems 92C17: Cell movement (chemotaxis, etc.)
Type
Research Papers
Information
Journal of Applied Probability , Volume 58 , Issue 1 , March 2021 , pp. 274 - 286
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Athreya, K. B. and Ney, P. E. (1968). Embedding of urn schemes into continuous time Markov branching processes and related limit theorems. Ann. Math. Statist. 39, 1801–1817.CrossRefGoogle Scholar
Athreya, K. B. and Ney, P. E. (1972). Branching Processes. Springer, New York.CrossRefGoogle Scholar
Balakrishnan, N. and Rao, C. R. (1998). Order statistics: an introduction. In Handbook of Statistics, Vol. 16, Order Statistics: Theory and Methods, eds N. Balakrishnan and C. R. Rao. Elsevier Science, Amsterdam, pp. 3–24.CrossRefGoogle Scholar
Billingsley, P. (1999). Convergence of Probability Measures, 2nd edn. Wiley, New York.CrossRefGoogle Scholar
Binder, B. J., Landman, K. A. and Simpson, M. J. (2008) Modeling proliferative tissue growth: a general approach and an avian case study. Phis. Rev. E, 78, 031912.CrossRefGoogle Scholar
Binder, B. J. and Landman, K. A. (2009). Exclusion processes on a growing domain. J. Theoret. Biol. 259, 541–551.CrossRefGoogle ScholarPubMed
Blackwell, D. and MacQueen, J. B. (1973). Ferguson distributions via Pólya urn schemes. Ann. Statist. 1, 353–355.CrossRefGoogle Scholar
Blom, G. and Holst, L. (1991). Embedding procedures for discrete problems in probability. Math. Scientist, 16, 29–40.Google Scholar
Cheliotis, D. and Kouloumpou, D. Functional limit theorems for the Pólya and q-Píya urns. Preprint, arXiv:1905.13336.Google Scholar
Csörgö, M. and Révész, P. (1978). Strong approximations of the quantile process. Ann. Statist. 6, 882–894.CrossRefGoogle Scholar
Csörgö, M. and Révész, P. (1981). Strong Approximations in Probability and Statistics. Academic Press, New York.Google Scholar
de La Fortelle, A. (2006). Yule process sample path asymptotics. Electron. Commun. Prob. 11, 193–199.CrossRefGoogle Scholar
Devroye, L., Mehrabian, A. and Reddad, T. (2018). The total variation distance between high-dimensional Gaussians. Preprint, arXiv:1810.08693.Google Scholar
Eggenberger, F. and Pólya, G. (1923). über die Statistik verketteter Vorgange. Z. Angew. Math. Mech. 3, 279–289.CrossRefGoogle Scholar
Goldstein, L. and Reinert, G. (2013). Stein’s method for the Beta distribution and the Pólya–Eggenberger urn. J. App. Prob. 50, 1187–1205.CrossRefGoogle Scholar
Hewitt, E. and Savage, L. J. (1955). Symmetric measures on Cartesian products. Trans. Amer. Math. Soc. 80, 470–501.CrossRefGoogle Scholar
Ikeda, S. and Matsunawa, T. (1972). On the uniform asymptotic normality of sample quantiles. Ann. Inst. Stat. Math. 24, 33–52.CrossRefGoogle Scholar
Janson, S. (2004). Functional limit theorems for multitype branching processes and generalized Pólya urns. Stoch. Process Appl. 110, 177–245.CrossRefGoogle Scholar
Janson, S. (2006). Limit theorems for triangular urn schemes. Prob. Theory Relat. Fields 134, 417–452.CrossRefGoogle Scholar
Johnson, N. L. and Kotz, S. (1977). Urn Models and Their Applications. Springer, New York.Google Scholar
Komlos, J., Major, P. and Tusnady, G. (1975). An approximation of partial sums of independent RVs and the sample DF. I. Z. Wahrscheinlichkeitsth. 32, 111–131.CrossRefGoogle Scholar
Kotz, S. and Balakrishnan, N. (1997). Advances in urn models during the past two decades. In Advances in Combinatorial Methods and Applications to Probability and Statistics, ed. N. Balakrishnan. Birkhäuser, Boston, pp. 203–257.CrossRefGoogle Scholar
Mahmoud, H. M. (2009). Pólya Urn Models. CRC Press, Boca Raton.Google Scholar
Markov, A. A. (1906). Extension of the law of large numbers to quantities depending on each other. Izv. fizm.-mat. obsch. Kazanskom univ. 2, 135–156 (in Russian). [Reprinted in J. Electron. Hist. Prob. Statist. 2, Article 10 (2006).]Google Scholar
Matsunawa, T. (1975). On the error evaluation of the joint normal approximation for sample quantiles. Ann. Inst. Statist. Math. 27, 189–199.CrossRefGoogle Scholar
Rachev, S. T., Klebanov, L. B., Stoyanov, S. V. and Fabozzi, F. (2013). The Methods of Distances in the Theory of Probability and Statistics. Springer, New York.CrossRefGoogle Scholar
Sazonov, V. V. (1975). On a bound for the rate of convergence in the multidimensional central limit theorem. In Proc. Sixth Berkeley Symp. on Math. Stat. and Prob., Berkeley and Los Angeles, University of California Press. Vol. 2, pp. 563–582.Google Scholar
Walker, A. M. (1968). A note on the asymptotic distribution of sample quantiles. J. R. Statist. Soc. B 30, 570–575.Google Scholar