Hostname: page-component-848d4c4894-mwx4w Total loading time: 0 Render date: 2024-06-26T11:51:20.831Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Number of Isolating Integrals in Systems with Three Degrees of Freedom

Published online by Cambridge University Press:  12 April 2016

Claude Froeschle
Claude Froeschle*
Affiliation:
Observatoire de Nice, Le Mont-Gros, 06 Nice (France)

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Dynamical systems with three degrees of freedom can be reduced to the study of a four-dimensional mapping. We consider here, as a model problem, the mapping given by the following equations:

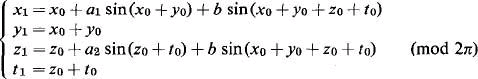
We have found that as soon as b ≠ 0, i.e. even for a very weak coupling, a dynamical system with three degrees of freedom has in general either two or zero isolating integrals (besides the usual energy integral).

Type
Research Article
Information
International Astronomical Union Colloquium , Volume 10: Gravitational N-Body Problem , November 1971 , pp. 110 - 117
Copyright
Copyright © Reidel 1971

References

Arnold, V. I. : private communication to Dr Hénon, M..Google Scholar
Contopoulos, G.: 1970, Cont. from the Ast. Dept. Univ. of Thessaloniki, No. 53.Google Scholar
Froeschle, C.: 1970, Astr. Astrophys. 4, 115.Google Scholar
Froeschle, C.: 1970, Astr. Astrophys. 5, 177.Google Scholar
Hénon, M.: 1969, Quart. Appl. Math. 27, 291.CrossRefGoogle Scholar
Poincaré, H.: 1892, Les Méthodes Nouvelles de la Mécanique Céleste, Gauthier-Villars, Paris.Google Scholar
Taylor, J. B.: 1969, private communication; see Culham Laboratory Progress Report CLM-PR-12.Google Scholar