1 Magnetized liner inertial fusion (MagLIF) concept
Magnetized liner inertial fusion (MagLIF) is an approach for thermonuclear fusion that is driven by Sandia’s Z pulsed power facility[Reference Matzen, Atherton, Cuneo, Donovan, Hall, Herrmann, Kiefer, Leeper, Leifeste, Long, McKee, Mehlhorn, Porter, Schneider, Struve, Stygar and Weinbrecht1]. More than 20 MA of drive current are channeled into a centimeter-sized deuterium filled beryllium liner. The resulting magnetic pressure implodes the liner and compresses the fuel therein. Since the involved time scales in the electric discharge and compression are too long to adiabatically heat cold fuel to fusion temperatures due to involved cooling rates, magnetization is used as a method to increase the temperature and reduce heat losses[Reference Slutz and Vesey2]. A dedicated, smaller pulsed power device is feeding electromagnetic coils and fired prior to the main Z discharge. This creates an axial magnetic field of about 10 T inside the liner, parallel to its axis. Shortly after Z fires, when the liner is barely starting to implode, the Z-Beamlet laser (ZBL)[Reference Rambo, Smith, Porter, Hurst, Speas, Adams, Garcia, Dawson, Thurston, Wakefield, Kellogg, Slattery, Ives, Broyles, Caird, Erlandson, Murray, Behrendt, Neilsen and Narduzzi3] delivers 2–4 kJ of laser light at 527 nm through a polyimide window into the fuel, creating a plasma with temperatures of several 100 eV. Since the charged particles of the plasma cannot freely move across field lines of the previously applied axial magnetic field (and vice versa), the magnetic field gets compressed and amplified once the liner implodes. This strong axial magnetic field forces electrons to spiral along the axis, which greatly reduces heat losses that would normally occur due to electron conduction. Figure 1 depicts the three main stages of the MagLIF concept, namely: early magnetization (left), laser heating (middle), and fuel compression (right). Early MagLIF experiments demonstrated that neutron yields increased dramatically if an initial B-field was applied and the fuel was pre-heated with ZBL. Either of these processes by themselves did not accomplish such an enhancement[Reference Gomez, Slutz, Sefkow, Hahn, Hansen, Knapp, Schmit, Ruiz, Sinars, Harding, Jennings, Awe, Geissel, Rovang, Smith, Chandler, Cooper, Cuneo, Harvey-Thompson, Herrmann, Hess, Lamppa, Martin, McBride, Peterson, Porter, Rochau, Savage, Schroen, Stygar and Vesey4]. One should note that the temperature of the ZBL pre-heated plasma does proportionally affect the expected fusion gain in the MagLIF concept. Therefore, it was decided to increase the available laser energy of the ZBL.

Figure 1. Three main stages of the MagLIF concept: (left) early magnetization in which the radial magnetic field line compress then Be liner while an axially external field is applied, (middle) laser heating via a long-pulse kJ-class laser yielding plasma temperatures of order 100 eV, (right) fuel compression and fusion neutron yield due to magnetic confinement.
2 ZBL energy upgrade
Until recently, ZBL operated at 2 kJ energy at 527 nm with 2 ns pulsewidth. This was sufficient for its primary backlighting mission, but it will not be enough for future laser heating requirements for MagLIF. In order to extract the 5 kJ (at 1054 nm) of energy stored in the eleven main ZBL amplifiers, one has to increase the laser pulsewidth which risks transverse stimulated Brillouin scattering (SBS) in the large scale vacuum spatial filter lenses. Consequently, ZBL’s single-frequency front-end laser was replaced with a phase modulation (PM) system that also required development of a PM failsafe system. Even with these enhancements ZBL’s front end remains relatively simple compared to the multi-pulse, multi-frequency modulation used on systems such as OMEGA EP[Reference Dorrer, Roides, Cuffney, Okishev, Bittle, Balonek, Consentino, Hill and Zuegel5], NIF[Reference Bowers, Burkhart, Cohen, Erbert, Heebner, Hermann and Jedlovec6], LMJ[Reference Gleyzea, Hares, Vidala, Becka, Dubertranda and Perrina7] and the SG-III laser[Reference Zhu, Zheng, Wei, Jing, Hu, Zhou, Feng, Wang, Peng, Liu, Chen, Ding, Lin, Guo, Dang and Deng8].
2.1 SBS suppression system
High fluence in nanosecond-pulsed kJ-class laser systems can lead to conditions that exceed the threshold for SBS. Because beam diameters in kJ lasers are typically ![]() ${\geqslant}30~\text{cm}$, the interaction length in optical components that is perpendicular to beam propagation, acting in combination with a sufficiently long pulse, allows amplification of an initially weak transverse reflection across the aperture. Upon reaching the SBS threshold transmission falls dramatically and the depleted incident energy is confined to a shallow layer below the entrance surface of the optical component. Continued growth of this side scattered wave, referred to as transverse SBS, induces additional nonlinear effects including stimulated Raman scattering (SRS), self-focusing, backward propagating SBS and perhaps higher-order interactions, and it will eventually result in damage to optical elements. Transverse SBS and its associated damage are observed almost exclusively in kJ-class lasers that employ large diameter optical elements.
${\geqslant}30~\text{cm}$, the interaction length in optical components that is perpendicular to beam propagation, acting in combination with a sufficiently long pulse, allows amplification of an initially weak transverse reflection across the aperture. Upon reaching the SBS threshold transmission falls dramatically and the depleted incident energy is confined to a shallow layer below the entrance surface of the optical component. Continued growth of this side scattered wave, referred to as transverse SBS, induces additional nonlinear effects including stimulated Raman scattering (SRS), self-focusing, backward propagating SBS and perhaps higher-order interactions, and it will eventually result in damage to optical elements. Transverse SBS and its associated damage are observed almost exclusively in kJ-class lasers that employ large diameter optical elements.
Theoretical treatments of SBS, including the transient regime appropriate for nanosecond kJ lasers, have been developed by various authors[Reference Valley9–Reference Yu and Meng12]. Observations of SBS leading to energy loss and subsequent damage are well documented[Reference Uy, Haw and Hsu13–Reference Kyrazis and Weiland15]. Detailed measurements of the SBS threshold at 351 nm, including observed damage and validation of predictions for transient behavior, were carried out in large diameter optics on the NOVA laser[Reference Murray, Ray Smith, Ehrlich, Kyrazis, Thompson, Weiland and Wilcox16].
Because transverse SBS poses such a great risk for damage, methods to suppress SBS have been developed and deployed in essentially all of the world’s major kJ-class laser systems[Reference Dorrer, Roides, Cuffney, Okishev, Bittle, Balonek, Consentino, Hill and Zuegel5–Reference Zhu, Zheng, Wei, Jing, Hu, Zhou, Feng, Wang, Peng, Liu, Chen, Ding, Lin, Guo, Dang and Deng8, Reference Dixit17]. Suppression of SBS usually relies on increasing the laser bandwidth using PM, which also requires compensating for the inevitable conversion of PM to amplitude modulation (AM)[Reference Cao, Lu, Li, Yin, Ma, Zhu and Fan18]. However, other non-PM methods to increase bandwidth have been explored[Reference Eimerl, Campbell, Krupke, Zweiback, Kruer, Marozas, Zuegel, Myatt, Kelly, Froula and McCrory19]. Because insufficient PM bandwidth or outright failure of PM can lead to extensive damage, all kJ lasers that suppress SBS using PM employ some form of PM failsafe system[Reference Thompson, Browning, Padilla, Weiland and Wintemute20].
The PM frequency, depth of modulation and therefore the total bandwidth adequate to suppress SBS can be estimated using the intrinsic Brillouin lifetime and gain of optical materials[Reference Murray, Ray Smith, Ehrlich, Kyrazis, Thompson, Weiland and Wilcox16, Reference Dixit17, Reference Heiman, Hamilton and Hellwarth21–Reference Belkov, Dolgopolov, Kochemasov, Kulikov, Soloveva, Sukharev and Voronich23]. Modulation using a single frequency ![]() ${\geqslant}3~\text{GHz}$ and a modulation index (MI)
${\geqslant}3~\text{GHz}$ and a modulation index (MI) ![]() ${\geqslant}5$ usually provides an adequate margin of safety for amplification in fibers and for conditions found in kJ lasers. In practice however, modulation schemes can involve multiple drive frequencies much higher than 3 GHz, for example in the front-end lasers that inject multi-beam kJ systems used for direct-drive inertial confinement fusion (ICF). An example of this type of front-end system is at the OMEGA EP Laser at the laboratory of laser energetics (LLE)[Reference Dorrer, Roides, Cuffney, Okishev, Bittle, Balonek, Consentino, Hill and Zuegel5], where complex temporal pulse shapes require multiple modulation frequencies up to 31.9 GHz and spatially uniform target illumination requires two-dimensional smoothing by spectral dispersion (SSD)[Reference Skupsky, Short, Kessler, Craxton, Letzring and Soures24, Reference Regan, Marozas, Craxton, Kelly, Donaldson, Jaanimagi, Jacobs-Perkins, Keck, Kessler, Meyerhofer, Sangster, Seka, Smalyuk, Skupsky and Zuegel25]. Because failure of any component of a multi-frequency PM scheme could compromise performance, or lead to serious damage, the PM failsafe systems for these complex front ends employ multiple levels of PM testing and validation.
${\geqslant}5$ usually provides an adequate margin of safety for amplification in fibers and for conditions found in kJ lasers. In practice however, modulation schemes can involve multiple drive frequencies much higher than 3 GHz, for example in the front-end lasers that inject multi-beam kJ systems used for direct-drive inertial confinement fusion (ICF). An example of this type of front-end system is at the OMEGA EP Laser at the laboratory of laser energetics (LLE)[Reference Dorrer, Roides, Cuffney, Okishev, Bittle, Balonek, Consentino, Hill and Zuegel5], where complex temporal pulse shapes require multiple modulation frequencies up to 31.9 GHz and spatially uniform target illumination requires two-dimensional smoothing by spectral dispersion (SSD)[Reference Skupsky, Short, Kessler, Craxton, Letzring and Soures24, Reference Regan, Marozas, Craxton, Kelly, Donaldson, Jaanimagi, Jacobs-Perkins, Keck, Kessler, Meyerhofer, Sangster, Seka, Smalyuk, Skupsky and Zuegel25]. Because failure of any component of a multi-frequency PM scheme could compromise performance, or lead to serious damage, the PM failsafe systems for these complex front ends employ multiple levels of PM testing and validation.
Using highly efficient waveguide modulators available today, obtaining a PM spectrum from continuous wave (CW) fiber lasers used in low-power front ends is simple, even for phase excursions of many radians and modulation frequencies beyond 30 GHz. Although ZBL does not currently employ SSD, where nanosecond pulse lengths dictate use of frequencies in the range of 17–18 GHz, anticipating future need for SSD suggests operating near that frequency range. While modulation frequency is one parameter that might influence the design of a PM failsafe system, it is only one among many. PM scheme complexity and the facility size also impacts failsafe design, where optical and electrical signal propagation times can impose limits for safely canceling a shot. For example, ZBL is housed in a single ![]() $11500~\text{ft}^{2}$ clean room facility, whereas NIF’s 192 beamlines occupy approximately
$11500~\text{ft}^{2}$ clean room facility, whereas NIF’s 192 beamlines occupy approximately ![]() $678000~\text{ft}^{2}$[26], the LLE occupies approximately
$678000~\text{ft}^{2}$[26], the LLE occupies approximately ![]() $82000~\text{ft}^{2}$[27], and LMJ is probably comparable to NIF in size[28].
$82000~\text{ft}^{2}$[27], and LMJ is probably comparable to NIF in size[28].
Given ZBL’s comparatively small size and the conceptual simplicity afforded by its pulse formats and single-frequency PM, we concluded that a suitable PM failsafe design could be based on monitoring a single parameter, namely continuous detection of an optical heterodyne signal. This signal can be derived prior to temporal pulse formatting and it can be autonomous with respect to timing signals used to fire ZBL, i.e., it operates independent of clock signals and responds to a PM failure condition whenever it occurs. And finally, heterodyne detection in a system composed almost entirely of single-mode polarization maintaining (SMPM) fiber and single-mode polarizing (PZ) fiber is simple to implement.
The method to derive a ‘trigger’ for the PM failsafe is illustrated by the spectra shown in Figure 2, where the main PM spectrum injected into ZBL has a modulation frequency of 14.8 GHz and MI of 5.52, and a reference PM spectrum has a frequency of 12.8 GHz and ![]() $\text{MI}_{\text{Ref}}=2.42$. A heterodyne beat note of 2 GHz is generated by interference of first-order sidebands, where the reference spectrum is optically filtered using an étalon to eliminate additional observable beat notes at 4 and 6 GHz. The first-order reference sideband could interfere with higher-order sidebands in the main PM spectrum and generate additional higher beat frequencies, but they exceed the detector bandwidth of 8 GHz. The choice of
$\text{MI}_{\text{Ref}}=2.42$. A heterodyne beat note of 2 GHz is generated by interference of first-order sidebands, where the reference spectrum is optically filtered using an étalon to eliminate additional observable beat notes at 4 and 6 GHz. The first-order reference sideband could interfere with higher-order sidebands in the main PM spectrum and generate additional higher beat frequencies, but they exceed the detector bandwidth of 8 GHz. The choice of ![]() $\text{MI}_{\text{Ref}}=2.42$ results in large first-order sidebands while
$\text{MI}_{\text{Ref}}=2.42$ results in large first-order sidebands while ![]() $\text{MI}_{\text{Main}}=5.52$ provides adequate bandwidth, and with zero carrier amplitude also provides a simple visual cue to system operators that the main PM is operating as expected. Although ZBL’s failsafe trigger itself is not constrained by timing signals, the two PM drive frequencies are phase locked to the facility’s main rubidium clock so that the heterodyne beat note maintains a fixed phase relative to all timing signals used in the system.
$\text{MI}_{\text{Main}}=5.52$ provides adequate bandwidth, and with zero carrier amplitude also provides a simple visual cue to system operators that the main PM is operating as expected. Although ZBL’s failsafe trigger itself is not constrained by timing signals, the two PM drive frequencies are phase locked to the facility’s main rubidium clock so that the heterodyne beat note maintains a fixed phase relative to all timing signals used in the system.

Figure 2. Plot of PM spectra for ![]() $\text{MI}=2.42$ (red) and
$\text{MI}=2.42$ (red) and ![]() $\text{MI}=5.52$ (blue) showing how first-order sideband interference generates a 2 GHz heterodyne beat note used to generate a PM failsafe trigger. The main modulation frequency is 14.8 GHz and the reference is 12.8 GHz. The solid red sideband represents the first-order sideband transmitted by an étalon.
$\text{MI}=5.52$ (blue) showing how first-order sideband interference generates a 2 GHz heterodyne beat note used to generate a PM failsafe trigger. The main modulation frequency is 14.8 GHz and the reference is 12.8 GHz. The solid red sideband represents the first-order sideband transmitted by an étalon.
A diagram of the optical assembly that generates the main PM spectrum injected into ZBL, and that also generates the heterodyne signal, is shown in Figure 3. With the exception of the custom-ordered phase modulators the entire assembly is built from commercial off-the-shelf (COTS) products. While the assembly is housed in an inexpensive rack-mount box, all optical components are mounted on a solid breadboard resting on sorbothane feet and sorbothane sheets sandwiched between plastic sheets lining the interior to reduce acoustic coupling. Although the optical path between the two ![]() $50/50$ fiber splitters effectively forms a Mach–Zehnder interferometer, acoustic perturbation is minimal and does not affect the heterodyne beat note stability.
$50/50$ fiber splitters effectively forms a Mach–Zehnder interferometer, acoustic perturbation is minimal and does not affect the heterodyne beat note stability.

Figure 3. Functional diagram of the optical assembly that generates the main PM spectrum injected into ZBL and that also generates the heterodyne signal that triggers the PM failsafe. Red lines with circles denote optical fibers. Mode matching lenses for the confocal scanning étalon, and its output collimating lens, are not shown. The étalon transmits only one first-order sideband of the reference PM spectrum.
The confocal étalon that filters the reference PM spectrum is locked to a first-order sideband using a simple dither lock, with dither frequency of approximately 8 kHz. Given the inherent long- and short-term frequency stability of the 1053 nm fiber laser and Invar construction of the étalon, lock can be maintained almost indefinitely. Demodulation using an analog lock-in amplifier generates the error signal that is sent to a servo controller to lock the etalon.
Electrical processing of the heterodyne beat note to generate the failsafe trigger consists of bandpass filtering at 2 GHz, multi-stage amplification, power conversion to a direct current (DC) level and final low-pass filtering with a cut-off frequency of about 750 MHz. The minimum bandwidth of the active components in this chain is about 4 GHz, and the passive radio frequency (RF) power detector’s bandwidth is also 4 GHz. The initial RF power in the heterodyne signal is about ![]() $20~\unicode[STIX]{x03BC}\text{W}$, and it rides on top of a DC pedestal resulting in part from integration of higher optical frequencies that exceed the 8 GHz bandwidth of the detector. Variable RF amplifier gain is used to adjust DC output from the power detector for compatibility with transistor–transistor logic (TTL) or complementary metal-oxide semiconductor (CMOS) logic levels. In its current configuration the DC trigger voltage is set for a TTL level that controls a 5 GHz high-isolation semiconductor switch.
$20~\unicode[STIX]{x03BC}\text{W}$, and it rides on top of a DC pedestal resulting in part from integration of higher optical frequencies that exceed the 8 GHz bandwidth of the detector. Variable RF amplifier gain is used to adjust DC output from the power detector for compatibility with transistor–transistor logic (TTL) or complementary metal-oxide semiconductor (CMOS) logic levels. In its current configuration the DC trigger voltage is set for a TTL level that controls a 5 GHz high-isolation semiconductor switch.
When a PM failure occurs that switch induces a high-to-low transition coupled out through a 250 mA, 180 MHz buffer that inhibits triggering of the delay generator that controls the ‘slicer’ Pockels cell following ZBL’s regenerative amplifier (regen). To eliminate the possibility that a glitch event triggers the failsafe but otherwise allows continued normal operation, the high-to-low transition triggers a one-shot that drives the base of a high bandwidth transistor for ![]() ${>}2~\text{ms}$ to latch the trigger to ground while relays shut off the RF power to the main phase modulator. This sequence of events makes a failure permanent until the system is reset by an operator. In the event of a PM failure during an actual laser shot, ZBL’s four-pass rod amplifier and main amplifiers would still fire but would produce nothing more than amplified spontaneous emission due to absence of the pulse from the regen.
${>}2~\text{ms}$ to latch the trigger to ground while relays shut off the RF power to the main phase modulator. This sequence of events makes a failure permanent until the system is reset by an operator. In the event of a PM failure during an actual laser shot, ZBL’s four-pass rod amplifier and main amplifiers would still fire but would produce nothing more than amplified spontaneous emission due to absence of the pulse from the regen.
The fiber laser front-end and the PM failsafe system are located in the master oscillator room (MOR) that is separate from the laser bay where ZBL is located. A pulse of light leaving the MOR propagates through 30 m of PZ fiber before injection into the first stage of amplification provided by ZBL’s regen. After a sufficient number of round trips in the regen, and a corresponding delay, the pulse is coupled out and a ‘slicer’ Pockels cell following the regen opens to allow propagation to the rest of the amplification chain while chopping out pre- and post-pulses. To provide a sufficient margin of safety the PM failsafe must sense the absence of PM with enough time to prevent the slicer from opening in the event of a PM failure. Using simulated instantaneous failures, we measured the margin of safety to be 35 ns. This means a pulse can enter the 30 m PZ fiber and a subsequent PM failure can be detected in the MOR, initiate the failsafe and block the pulse at the slicer Pockels cell. In this scenario involving an instantaneous failure, a pulse that likely has an appropriate PM spectrum would be stopped after the regen.
Fundamental to achieving a reasonable margin of safety for an instantaneous PM failure is a failsafe system that responds on nanosecond time scales. Figure 4 shows the transition time after the heterodyne signal is intentionally interrupted using an RF switch with a 5 GHz bandwidth. The time of 30 ns shown in Figure 4 is measured from switch closure until the 1 V crossing time on a high-to-low transition of the failsafe output, where 1 V corresponds approximately to the threshold for the trigger-inhibit input of the delay generator that controls the slicer Pockels cell. The transition time is set by adjusting amplification of the heterodyne signal prior to power conversion, with the least time occurring as the DC level of the trigger approaches the TTL threshold of the high isolation switch. The transition time can be adjusted from about 22 to 40 ns; however, operating the system too close to the TTL threshold can result in undesirable instability. We find stable operation is obtained for transition times of 30–34 ns, where longer transition times are also undesirable.

Figure 4. An example of a 30 ns transition time from high to ground for the PM failsafe system. A monitor output for the 2 GHz heterodyne beat note is shown in red, and the output of the 180 MHz buffer into ![]() $50~\unicode[STIX]{x03A9}$ on a 12 GHz oscilloscope is shown in blue. The transition time to a level of 1 V, approximately the trigger-inhibit threshold for an SRS DG535 delay generator equipped with an optional inhibit input, is adjustable from about 22–40 ns. Note that the 35 ns margin of safety described in the text is measured relative to the time when the falling edge of the failsafe signal crosses this 1 V threshold.
$50~\unicode[STIX]{x03A9}$ on a 12 GHz oscilloscope is shown in blue. The transition time to a level of 1 V, approximately the trigger-inhibit threshold for an SRS DG535 delay generator equipped with an optional inhibit input, is adjustable from about 22–40 ns. Note that the 35 ns margin of safety described in the text is measured relative to the time when the falling edge of the failsafe signal crosses this 1 V threshold.
Another important consideration is the value of the modulation index that triggers a failsafe event. This is measured by adjusting the main phase modulator’s RF power until the change in amplitude of its first-order sideband triggers a failure. During this measurement ![]() $\text{MI}_{\text{Ref}}$ remains unchanged. Decreasing the RF power triggers a failsafe event at
$\text{MI}_{\text{Ref}}$ remains unchanged. Decreasing the RF power triggers a failsafe event at ![]() $\text{MI}_{\text{Main}}\approx 4.5$ and increasing the RF power triggers the failsafe at
$\text{MI}_{\text{Main}}\approx 4.5$ and increasing the RF power triggers the failsafe at ![]() $\text{MI}_{\text{Main}}\approx 6.2$, although the resulting increase in bandwidth from higher RF power is not an important consideration. For the maximum energy of about 4.5 kJ that ZBL can currently produce, PM spectra for both failure points provide adequate bandwidth to maintain operating conditions below the SBS threshold. Figure 5 shows the nominal PM spectrum for
$\text{MI}_{\text{Main}}\approx 6.2$, although the resulting increase in bandwidth from higher RF power is not an important consideration. For the maximum energy of about 4.5 kJ that ZBL can currently produce, PM spectra for both failure points provide adequate bandwidth to maintain operating conditions below the SBS threshold. Figure 5 shows the nominal PM spectrum for ![]() $\text{MI}_{\text{Main}}=5.52$ and spectra for the two MI values where failsafe events occur.
$\text{MI}_{\text{Main}}=5.52$ and spectra for the two MI values where failsafe events occur.

Figure 5. The PM spectrum for the nominal value of ![]() $\text{MI}_{\text{Main}}=5.52$ and the spectra for
$\text{MI}_{\text{Main}}=5.52$ and the spectra for ![]() $\text{MI}_{\text{Main}}=4.5$ and
$\text{MI}_{\text{Main}}=4.5$ and ![]() $\text{MI}_{\text{Main}}=6.2$, where the first-order sideband amplitude is diminished sufficiently to result in a PM failsafe event. All three PM spectra are plotted on the same vertical scale. Both modulation frequencies and the resulting heterodyne beat note frequency remain unchanged during these measurements.
$\text{MI}_{\text{Main}}=6.2$, where the first-order sideband amplitude is diminished sufficiently to result in a PM failsafe event. All three PM spectra are plotted on the same vertical scale. Both modulation frequencies and the resulting heterodyne beat note frequency remain unchanged during these measurements.
A final consideration is the change in main PM drive frequency that would result in a failsafe event. Although a direct measurement cannot be easily carried out on the fully assembled system, its value can be inferred from the transmission characteristics of the 2 GHz bandpass filter that is the first element in the electrical processing of the heterodyne signal. Assuming 5–6 dB of attenuation (which we know from previous system characterization corresponds to greater reduction in the heterodyne power than occurs at either ![]() $\text{MI}_{\text{Main}}$ associated with the failsafe events discussed above), we can infer the main PM frequency difference from the resulting change in the heterodyne signal. Increasing or decreasing the PM frequency by
$\text{MI}_{\text{Main}}$ associated with the failsafe events discussed above), we can infer the main PM frequency difference from the resulting change in the heterodyne signal. Increasing or decreasing the PM frequency by ![]() ${\sim}600~\text{MHz}$ results in at least 5–6 dB of attenuation according to data sheets provided by the vendor for the 2 GHz bandpass filter. Thus the required changes are small relative to the main PM frequency of 14.8 GHz. Given that a PM frequency of 3 GHz is sufficient for SBS suppression, the failsafe provides adequate protection against frequency drift. A more detailed description of the SBS suppression system and its associated failsafe system can be found here[Reference Rambo, Armstrong, Schwarz, Smith, Shores, Shane Speas and Porter29, Reference Armstrong30].
${\sim}600~\text{MHz}$ results in at least 5–6 dB of attenuation according to data sheets provided by the vendor for the 2 GHz bandpass filter. Thus the required changes are small relative to the main PM frequency of 14.8 GHz. Given that a PM frequency of 3 GHz is sufficient for SBS suppression, the failsafe provides adequate protection against frequency drift. A more detailed description of the SBS suppression system and its associated failsafe system can be found here[Reference Rambo, Armstrong, Schwarz, Smith, Shores, Shane Speas and Porter29, Reference Armstrong30].
2.1.1 PM to AM suppression
The amplified, PM pulse is sent through 30 m of PM fiber to the fiber output collimator at the input of the ZBL ring-regenerative amplifier. Due to the spectral dispersion in the fiber, one can observe a 14.8 GHz AM on the order of 10% of peak signal. This PM to AM conversion was successfully suppressed by pre-compensating this spectral dispersion via a temporal grating compressor at the input of the fiber run.
The output of the regen shows significant PM to AM conversion as well, because the gain profile is not constant across all frequency sidebands. This differential gain was reversed by placing a birefringent filter (BRF) inside the regen cavity. The BRF acts as a spectral filter that can be tuned to cause additional losses at the higher or lower (as needed) frequency band, in order to compensate the differential gain seen by some sidebands.
2.1.2 Demonstrating increased laser energy
Once we verified that we can indeed efficiently suppress any PM to AM conversion and have a robust PM failsafe in place, we slowly increased the laser pulsewidth and laser energy by increasing the rod amplifier seed into the main amplifiers. Figure 6 shows temporal diode traces of the frequency doubled ZBL beam for various pulsewidths and laser energies. One can see that the output energy doubles as one goes from 2 ns full width at half maximum (FWHM) to 4 ns FWHM.

Figure 6. Frequency doubled laser energy versus pulsewidth.
2.2 Installation of additional booster amplifiers
An obvious way to adding more laser energy to the current ZBL beam is adding booster amplifiers. Beamlet (the ZBL predecessor at Livermore) was originally designed for eleven main amplifiers and five additional booster amps. Each ZBL main amplifier housing currently contains one laser slab at the top level and one absorber slab at the bottom level since the bottom beamline is not used. Each slab stores about 500 J of energy for a total of 8 kJ at 1054 nm (referred to as ![]() $1\unicode[STIX]{x1D714}$) and corresponding 6 kJ at 527 nm (referred to as
$1\unicode[STIX]{x1D714}$) and corresponding 6 kJ at 527 nm (referred to as ![]() $2\unicode[STIX]{x1D714}$). As of now, we have added one booster amplifier for a maximum
$2\unicode[STIX]{x1D714}$). As of now, we have added one booster amplifier for a maximum ![]() $2\unicode[STIX]{x1D714}$ energy of 4.5 kJ at 4 ns. The current absence of additional electrical pulsed power infrastructure limits the addition of further booster activation. However, we are planning to upgrade Z-Petawatt laser (ZPW)[Reference Schwarz, Rambo, Geissel, Edens, Smith, Brambrink, Kimmel and Atherton31] to full aperture beam size in the near future, at which point we will modify our linear ten main amplifier chain to a five amplifier wrap-around
$2\unicode[STIX]{x1D714}$ energy of 4.5 kJ at 4 ns. The current absence of additional electrical pulsed power infrastructure limits the addition of further booster activation. However, we are planning to upgrade Z-Petawatt laser (ZPW)[Reference Schwarz, Rambo, Geissel, Edens, Smith, Brambrink, Kimmel and Atherton31] to full aperture beam size in the near future, at which point we will modify our linear ten main amplifier chain to a five amplifier wrap-around ![]() $1\times 2$ configuration (see Figure 7). This will liberate five pulsed power circuits which can be re-appropriated for further ZBL booster activation.
$1\times 2$ configuration (see Figure 7). This will liberate five pulsed power circuits which can be re-appropriated for further ZBL booster activation.

Figure 7. ZPW main amplifier configuration after full beam aperture upgrade. In this configuration, the top and bottom level of the amplifier contain laser glass for a total of 10 laser slabs. The full aperture beam enters the top level of the amplifier housing (top right) and wraps around to the lower level laser slabs, where it is retro-reflected by a mirror. In this way, one can preserve the same total gain of 10 amplifier slabs while cutting the pulsed power requirements in half.
3 Upgrading ZPW for long-pulse mode
Another way to add energy for MagLIF is to add energy from a second laser. Therefore, it has been decided that the ZPW would be modified to operate in short- or long-pulse mode with an additional beam aperture increase from the current 16 cm round beam to ![]() $30~\text{cm}\times 30~\text{cm}$ beam. Going to full aperture and long-pulse mode, ZPW should also be able to extract up to 5 kJ of 1054 nm light. It should be noted that one cannot simply use a stretched broad-band seed beam in order to accomplish this task. For a chirped pulse, gain narrowing will cause pulse shortening in the amplifiers which will lead to nonlinear optical damage. Hence, our optical parametric chirped pulse amplification (OPCPA) front end had to be modified for single-frequency, long-pulse operation.
$30~\text{cm}\times 30~\text{cm}$ beam. Going to full aperture and long-pulse mode, ZPW should also be able to extract up to 5 kJ of 1054 nm light. It should be noted that one cannot simply use a stretched broad-band seed beam in order to accomplish this task. For a chirped pulse, gain narrowing will cause pulse shortening in the amplifiers which will lead to nonlinear optical damage. Hence, our optical parametric chirped pulse amplification (OPCPA) front end had to be modified for single-frequency, long-pulse operation.
3.1 Modifying OPCPA for long-pulse operation
A detailed description of our OPCPA system can be found elsewhere[Reference Schwarz, Rambo, Geissel, Kimmel, Brambrink, Atherton and Glassman32]. That system is seeded with a stretched 2.5 ns pulse from a Ti:sapphire laser that is tuned to 1053.5 nm. This chirped pulsewidth matches the pump pulsewidth of the OPCPA pump laser. For the modified front end, we have added a second alternate seed source based on a chopped single longitudinal mode (SLM) CW laser. When this SLM seed enters the OPCPA system with the chirped beam blocked, it is being amplified via the same optical parametric amplification (OPA) process as was the chirped fs seed. The amplified beam exiting the OPA then has a pulsewidth of 2.5 ns (based on the width of the pump pulse) at an energy of 45 mJ. During implementation of the alternate seed source, it was decided that we needed to upgrade the performance of the legacy OPCPA. We improved the energy stability of the pump laser, changed relay telescopes for improved pump beam size and beam quality, changed coating descriptions on optics and most significantly exchanged the old BBO crystals with LBO in the first two stages. All these improvements led to a slightly broader bandwidth (8–10 nm FWHM), better energy and pointing stability, higher damage threshold and improved temporal control of the amplified seed exiting the OPA system. Figure 8 shows a schematic of the modified OPCPA/OPA system. In order to extract the maximum energy of 5 kJ at 1054 nm from the long-pulse ZPW system, one has to increase the current sub-aperture beam of 16 cm round to the full aperture of ![]() $33~\text{cm}\times 33~\text{cm}$. At this point, one would have to install an SBS suppression system similar to the one described earlier. Since we operate the main amplifier system in double pass (not four-pass as is most common for such systems) one requires a correspondingly higher seed energy into the main amplifiers. Hence we upgraded our rod amplifier section as well (see Figure 9). It now includes an additional double passed 45 and 64 mm diameter rod amplifier for a total output energy of up to 50 J. Taking this approach leads to more B-Integral than a lower energy rod amplifier followed by a 4-pass main amplifier (like ZBL). As such, this higher energy front-end design requires a balance between pulsewidth and energy outputs in order to minimize nonlinear effects.
$33~\text{cm}\times 33~\text{cm}$. At this point, one would have to install an SBS suppression system similar to the one described earlier. Since we operate the main amplifier system in double pass (not four-pass as is most common for such systems) one requires a correspondingly higher seed energy into the main amplifiers. Hence we upgraded our rod amplifier section as well (see Figure 9). It now includes an additional double passed 45 and 64 mm diameter rod amplifier for a total output energy of up to 50 J. Taking this approach leads to more B-Integral than a lower energy rod amplifier followed by a 4-pass main amplifier (like ZBL). As such, this higher energy front-end design requires a balance between pulsewidth and energy outputs in order to minimize nonlinear effects.

Figure 8. Schematic of the modified OPCPA system. One can see that the system can be either seeded with an SLM laser (100 pJ) or a stretched short pulse seed (375 pJ). Either pulse is amplified in the first stage by a walk-off compensated double LBO stage (![]() $2~\text{mm}\times 25~\text{mm}$ crystals). The same technique is used for OPA stage 2 (
$2~\text{mm}\times 25~\text{mm}$ crystals). The same technique is used for OPA stage 2 (![]() $2~\text{mm}\times 13~\text{mm}$ crystals) with a final amplification in a single BBO crystal. The output beam has a flat-top beam size of 4 mm FWHM and 45 mJ energy at 10 Hz repetition rate.
$2~\text{mm}\times 13~\text{mm}$ crystals) with a final amplification in a single BBO crystal. The output beam has a flat-top beam size of 4 mm FWHM and 45 mJ energy at 10 Hz repetition rate.

Figure 9. Schematic of the modified rod amplifier section. A ![]() $=$ aperture, VSF
$=$ aperture, VSF ![]() $=$ vacuum spatial filter, QWP
$=$ vacuum spatial filter, QWP ![]() $=$ quarter-wave plate, FI
$=$ quarter-wave plate, FI ![]() $=$ faraday isolator, PC
$=$ faraday isolator, PC ![]() $=$ Pockels cell.
$=$ Pockels cell.
3.2 Adding infrastructure to co-inject and co-propagate ZPW with ZBL
Having a long-pulse ZPW beam in place now requires the ability to co-inject and co-propagate this beam along the ZBL beamline into the Z center section. Figure 10 shows a bird’s-eye view of the Z-backlighter facility (bottom) and the Z pulsed power facility (top). Both lasers are located at the south Z-backlighter building from which they propagate through the target bay (middle building) to the Z facility (top). The target bay houses the large ZPW temporal compressor and foure stand-alone target chambers (not all shown) for high energy density experiments and prototyping of Z diagnostics. The idea is to implement a dichroic beam combination on top of the mezzanine in the laser building. Figure 11 depicts the frequency doubled ZBL beam passing straight through a dichroic combiner[Reference Bellum, Field, Kletecka, Rambo and Smith33]. A beam pick-off mirror is inserted at the ZPW laser end that re-directs the beam over to the ZBL side where the 1054 nm beam is reflected off that same dichroic combiner. Similarly, any residual 1054 nm light in ZBL is now stripped by the combiner. ZPW will frequency double in the subsequent second harmonic crystal while the ZBL beam remains unchanged because its polarization is orthogonal to the nonlinear birefringent crystal axis. We have completed the co-injection of a sub-aperture long-pulse ZPW beam with ZBL and are currently working on the frequency doubling of ZPW. We are expecting up to 400 J at 527 nm at sub-aperture and up to 3 kJ at full aperture in the future.

Figure 10. Bird’s-eye view of the Z-backlighter facility (Building 986, bottom) and the Z pulsed power facility (Building 983, top). Building 986 houses ZBL and ZPW. Both lasers can be sent (separately or co-injected) into the Target Bay for stand-alone experiments in up to four dedicated target chambers. A single beamline connects the Target Bay and the Z pulsed power facility. This beamline is currently used by ZBL only in order to provide pre-heating of MagLIF fuel or x-ray backlighting for various other experiments.
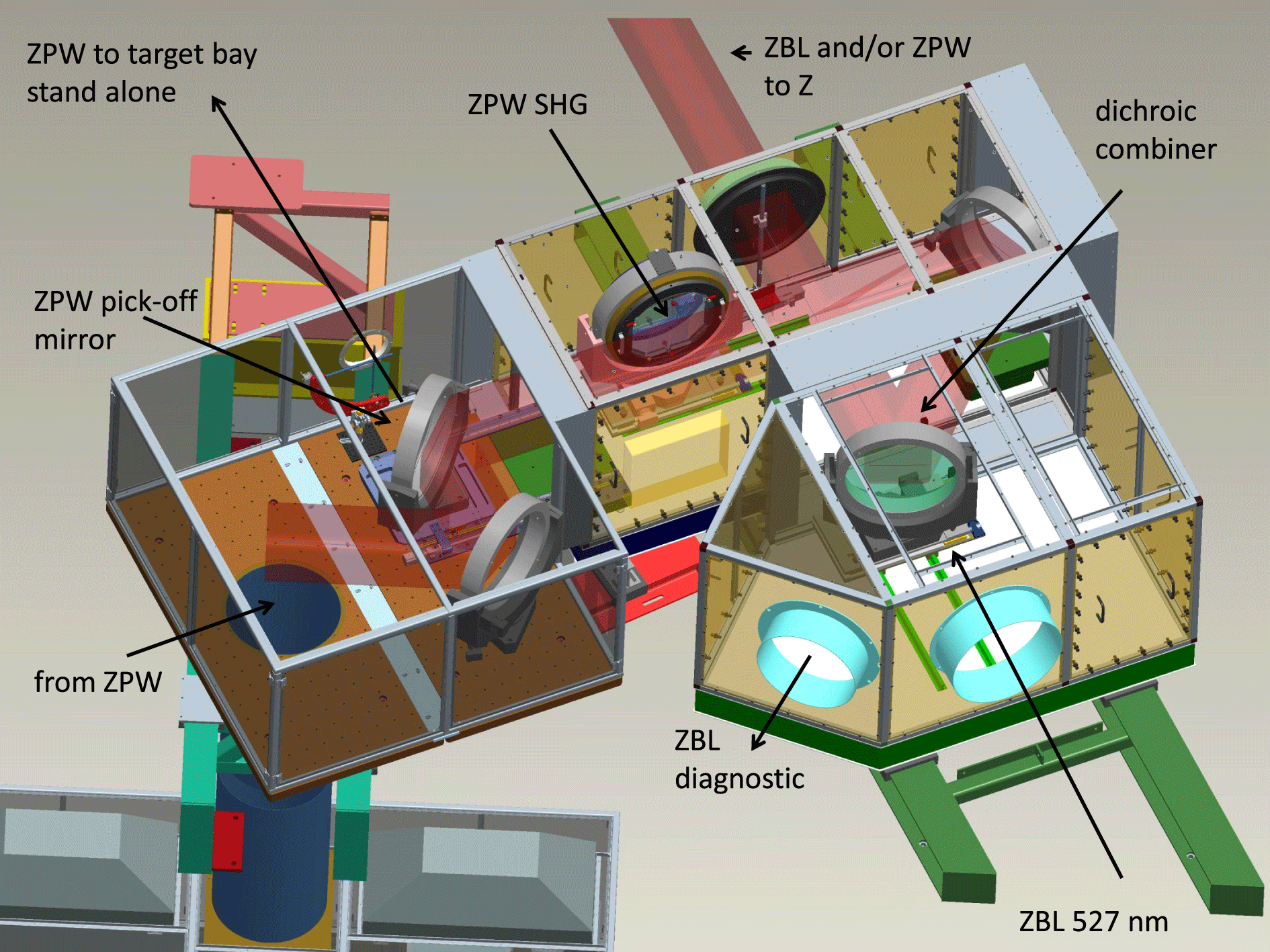
Figure 11. Schematic of the ZPW and ZBL co-injection area.
4 Explore possible MagLIF backlighting
Having ZPW operating in short- and long-pulse mode opens up the possibility of backlighting an MagLIF experiment using ZPW while ZBL acts as the heating beam.
4.1 Scenario 1: short-pulse PW
In this backlighting scenario, one would operate ZPW in the short-pulse mode. The beam would not be combined with ZBL at the building 986 mezzanine, but would be temporally compressed in the temporal compressor chamber located in the target bay (see Figure 10). At the exit of the temporal compressor, the beam would then be combined with ZBL using a dichroic combiner. This infrastructure already exists. The final optics assembly (FOA) in the Z facility would dichroicly split the two beams. ZBL can be reflected down into the Be liner (as usual) while ZPW passes through the dichroic separator before it is focused by a second lens to an off-axis target for x-ray backlighting (see Figure 12 option 1). Note that ZPW cannot be fully compressed in this scenario due to filamentation and beam breakup concerns in the focusing lens. B-Integral calculations show that 500 J at 250 ps would be a safe operating point for a sub-aperture beam. This backlighting option will have more energy than option 2 (see below), because one does not lose energy during frequency conversion. Furthermore, the higher intensity short pulse should allow the creation of higher energy x-rays ![]() ${>}8~\text{keV}$ which would allow us to probe high plasma density at stagnation. A large area plasma electrode Pockels cell (PEPC) is used at the output of the main amplifiers to prevent target backreflection from being amplified which could damage the laser system.
${>}8~\text{keV}$ which would allow us to probe high plasma density at stagnation. A large area plasma electrode Pockels cell (PEPC) is used at the output of the main amplifiers to prevent target backreflection from being amplified which could damage the laser system.
4.2 Scenario 2: long-pulse PW
In the long-pulse PW scenario (see Figure 12 option 2), one would use the frequency doubled co-injected beam (as described above) in conjunction with a polarizing beam splitter in the FOA. Even though one would lose some energy during frequency conversion, the higher laser to x-ray conversion would compensate the loss. Furthermore, using the second harmonic light provides an inherent safety for backreflection protection. One should note that we still have the PEPC for backreflection protection of residual 1054 nm light. Since this beam would be on the order of ns pulsewidth, it would only produce x-rays below 8 keV.

Figure 12. Comparison between short- and long-pulse backlighting scenarios for MagLIF.

Figure 13. Comparison of laser illumination without a phase plate and defocused (left) and a similar sized illumination with a ![]() $750~\unicode[STIX]{x03BC}\text{m}$ phase plate at best focus. The images are scaled logarithmically to enhance lower intensity features of the spot without phase plate. The high intensity areas in the unconditioned beam (without phase plate) can cause filamentation and LPI amplification.
$750~\unicode[STIX]{x03BC}\text{m}$ phase plate at best focus. The images are scaled logarithmically to enhance lower intensity features of the spot without phase plate. The high intensity areas in the unconditioned beam (without phase plate) can cause filamentation and LPI amplification.
5 Control laser beam shape
The ZBL laser was originally designed and constructed at Lawrence Livermore National Laboratory as the Beamlet prototype for the National Ignition Facility (NIF) laser system. It was equipped with a 15 cm scale, multi-actuator deformable mirror (DFM)[Reference Hartley, Kartz, Behrendt, Hines, Pollock, Bliss, Thaddeus Salmon, Winters, Van Wonterghem and Zacharias34] in order to compensate static, thermal and on-shot aberrations. After the laser was decommissioned and brought to Sandia National Laboratories (SNL) this capability could not be retained because of the custom, prototype nature of the adaptive optics (AO) solution.
For many years, the primary mission of ZBL has been backlighting of high energy density events[Reference Bennett, Sinars, Wenger, Cuneo, Adams, Barnard, Beutler, Burr, Campbell, Claus, Foresi, Johnson, Keller, Lackey, Leifeste, McPherson, Mulville, Neely, Rambo, Rovang, Ruggles, Porter, Simpson, Smith and Speas35] at the center of the Z-accelerator. In the bent crystal backlighting technique employed[Reference Sinars, Cuneo, Bennett, Wenger, Ruggles, Vargas, Porter, Adams, Johnson, Keller, Rambo, Rovang, Seamen, Simpson, Smith and Speas36] the laser source size is of minor importance with respect to spatial resolution. Hence, there has been no programmatic need for the implementation of an AO system at ZBL. However, for MagLIF experiments focal spot control is of paramount importance because it will dramatically affect the laser plasma interactions (LPI) at the laser entrance hole (LEH) of the MagLIF liner. Two methods of focal spot control are presented below: passive control of the focal spot via a phase plate and active control via an AO system. Both approaches are currently pursued for MagLIF since it is not clear at this point if a large focal spot on then LEH (via phase plate) or a beam focus/defocus on the LEH (controlled via AO) is the best approach for depositing energy into the fuel. Furthermore, Z-beamlet is still mostly used as a backlighter laser and in this case we have shown that the conversion efficiency into x-rays is dramatically improved (by up to a factor 5) when the AO system is used.
5.1 Passive control: phase plates
To minimize LPI build-up at the LEH, one can lower the laser intensity by defocusing the laser to the anticipated ideal spot size. Without additional optical elements, this leads to an ill-defined intensity distribution caused by an ‘intermediate’ imaging plane, which is neither the relay-imaged near-field of the collimated beam nor its far-field (FF) Fourier plane equivalent, i.e., the plane of best focus. Defocused near flat-top beams of high energy lasers, which lack a perfect Gaussian cross-section and have significant phase distortions, are prone to very strong modulations and irregular hot-spot distributions. Consequently, just defocusing a beam is not a good method for reducing LPI. A better solution is to control the spot size in the focal plane by using random phase plates or their better defined successors, the distributed phase plates[Reference Kessler, Lin, Joseph Armstrong and Velazquez37]. These optical elements effectively scramble the phase front information and project laser light to a pre-defined area. Local phase front and intensity variations are averaged over the whole illuminated area. In this process, rays from wide ranging areas of the phase plate interfere in the focal plane and cause speckles which also exhibit a deep modulation. Fortunately, heat conduction in a plasma acts fast enough over the small scale of a speckle to reduce temperature gradient driven filamentation. A comparison of measured laser spots with and without phase plate are shown in Figure 13. In order to characterize the impact of phase plates on LPI, we performed measurements on stand-alone targets (without firing Z itself) that had an applied B-field of 9.5 T. SBS target reflection was diagnosed by placing a target-facing fiber into the soft edge of the laser beam. The light that is captured by this fiber is analyzed by a streaked visible spectrometer (SVS). All experiments used a 500 ps pre-pulse to decompress the window, aiding in better laser penetration overall. Figure 14 shows the streaked spectrum for a 4 kJ shot with phase plate (top) and a 2 kJ shot without phase plate (bottom). The beam sizes were 1.8 and 0.7 mm, respectively. One can clearly see a pre-pulse in both images. The SBS spectral broadening from this pre-pulse is similar in both cases because the pulse interacts with a solid-state density polyimide entrance window. Once the window is ‘blown away’, the main pulse interacts with the low density gas fuel behind it. At that point, one can clearly see a reduction of SBS from the phase plate compared to the defocused beam.

Figure 14. Comparison of a 4 kJ shot with a phase plate (top) and a 2 kJ shot with unconditioned beam at roughly ![]() $700~\unicode[STIX]{x03BC}\text{m}$ diameter (bottom). Despite the higher energy, there is a dramatic reduction of SBS for the case with a large diameter focal spot.
$700~\unicode[STIX]{x03BC}\text{m}$ diameter (bottom). Despite the higher energy, there is a dramatic reduction of SBS for the case with a large diameter focal spot.
A comparison of LEH transmission with and without phase plate clearly demonstrates the benefit of a smoother, conditioned beam. This aspect was measured by focusing a ZBL beam on an LEH window in a stand-alone target chamber with no B-field capability. Transmission was measured through the LEH window using a ![]() $40~\text{cm}\times 40~\text{cm}$ large scale calorimeter after beam expansion. Table 1 shows the results for two transmission measurements through a
$40~\text{cm}\times 40~\text{cm}$ large scale calorimeter after beam expansion. Table 1 shows the results for two transmission measurements through a ![]() $1~\unicode[STIX]{x03BC}\text{m}$ thick polyester foil with a defocused beam (the spot size is about 1 mm) and with a large phase plate spot of 2 mm FWHM, where the ‘maximum’ is chosen to be the average intensity of the speckled center region of the focus rather than the highest speckle intensity. Even though the much smaller spot would heat the foil much more easily and therefore penetrate better in the absence of LPI, the large and conditioned beam shows much more laser penetration. While more precise measurements are on the way, the benefit of suitable phase plates for MagLIF was already demonstrated at Sandia National Laboratories. The MagLIF programme is now in the process of optimizing laser intensity for the pre-heat phase of the experiments with dedicated phase plates. Note: Since the time this paper was accpeted, we have now achieved main pulse window transmission of up to 90%.
$1~\unicode[STIX]{x03BC}\text{m}$ thick polyester foil with a defocused beam (the spot size is about 1 mm) and with a large phase plate spot of 2 mm FWHM, where the ‘maximum’ is chosen to be the average intensity of the speckled center region of the focus rather than the highest speckle intensity. Even though the much smaller spot would heat the foil much more easily and therefore penetrate better in the absence of LPI, the large and conditioned beam shows much more laser penetration. While more precise measurements are on the way, the benefit of suitable phase plates for MagLIF was already demonstrated at Sandia National Laboratories. The MagLIF programme is now in the process of optimizing laser intensity for the pre-heat phase of the experiments with dedicated phase plates. Note: Since the time this paper was accpeted, we have now achieved main pulse window transmission of up to 90%.
Table 1. Comparison of window penetration with and without phase plate.

5.2 Active control: adaptive optics
Figure 15(a) shows a rough schematic of the past ZBL architecture. ZBL consists of a pulsed fiber laser front end with variable pulse-shape control that gets pre-amplified in a ring-regenerative amplifier. Before amplification in a 4-pass rod amplifier, the beam intensity profile gets shaped into a square flat-top beam at the rod amp input (RAI). After the 4-pass rod amplifier, amplification to the kJ level occurs in the 4-pass large area slab amplifiers before the beam gets frequency doubled in a KDP crystal and sent onto a target in the Z center section.

Figure 15. Existing (a) and modified (b) ZBL architecture in order to accommodate the need for an AO system.
Figure 15(b) depicts the modified ZBL system layout with the DFM being located at the rod amp output (RAO). An SID4 wavefront sensor (WFS) from Phasics is located at the ![]() $1\unicode[STIX]{x1D714}$ diagnostics box which senses all aberrations up to this point. A closed loop control software (also from Phasics; http://www.phasics.fr) can then post-compensate for beam distortions in the rod amplifier and pre-compensate on-shot main amplifier aberrations.
$1\unicode[STIX]{x1D714}$ diagnostics box which senses all aberrations up to this point. A closed loop control software (also from Phasics; http://www.phasics.fr) can then post-compensate for beam distortions in the rod amplifier and pre-compensate on-shot main amplifier aberrations.
The 41-actuator bimorph DFM (DM2-90-41) was purchased from NightN (www.nightn.ru) together with the electronic HV control unit (CDM-41-300U). Size and actuator pattern of the bimorph was based on the ![]() $5~\text{cm}\times 5~\text{cm}$ laser beam size at the RAO. 36 actuators cover a square active area of
$5~\text{cm}\times 5~\text{cm}$ laser beam size at the RAO. 36 actuators cover a square active area of ![]() $6~\text{cm}\times 6~\text{cm}$ within a clear aperture of 9 cm diameter. The number one electrode is special in that it provides a global (de-)focus term whereas electrodes 38–41 provide astigmatism control.
$6~\text{cm}\times 6~\text{cm}$ within a clear aperture of 9 cm diameter. The number one electrode is special in that it provides a global (de-)focus term whereas electrodes 38–41 provide astigmatism control.
Our wavefront control relies on the WFS located at a near-field (NF) image plane inside the ![]() $1\unicode[STIX]{x1D714}$ diagnostic box up on the mezzanine in building 986. In this configuration, beam aberrations can be compensated until just prior to the frequency doubling crystal. A major challenge in most wavefront sensing allocations is the problem of finding a perfectly ‘flat wavefront’ that the WFS can be calibrated against. In our case, for example, the WFS factory calibration cannot be used, because the sensor would measure the laser beam train aberrations plus the aberrations from the down-collimating optics in the
$1\unicode[STIX]{x1D714}$ diagnostic box up on the mezzanine in building 986. In this configuration, beam aberrations can be compensated until just prior to the frequency doubling crystal. A major challenge in most wavefront sensing allocations is the problem of finding a perfectly ‘flat wavefront’ that the WFS can be calibrated against. In our case, for example, the WFS factory calibration cannot be used, because the sensor would measure the laser beam train aberrations plus the aberrations from the down-collimating optics in the ![]() $1\unicode[STIX]{x1D714}$ sensor package. In order to remove the diagnostic aberrations one has to create a perfect wavefront at the diagnostic input, measure the beam distortions and then later subtract them. In our case, this plane wavefront is created by illuminating a diffraction limited pinhole in the transport spatial filter (TSF) using the CW
$1\unicode[STIX]{x1D714}$ sensor package. In order to remove the diagnostic aberrations one has to create a perfect wavefront at the diagnostic input, measure the beam distortions and then later subtract them. In our case, this plane wavefront is created by illuminating a diffraction limited pinhole in the transport spatial filter (TSF) using the CW ![]() $1\unicode[STIX]{x1D714}$ alignment beam. This creates a point source that is re-collimated by the L4 lens and sent into the diagnostic package. The measured aberrations (see Figure 16) are solely due to the diagnostic optics (assuming that L4 lens and subsequent three mirrors are perfect).
$1\unicode[STIX]{x1D714}$ alignment beam. This creates a point source that is re-collimated by the L4 lens and sent into the diagnostic package. The measured aberrations (see Figure 16) are solely due to the diagnostic optics (assuming that L4 lens and subsequent three mirrors are perfect).

Figure 16. Phasics software screenshot of calibration measurement.
Note that the beam NF has a circular, Gaussian intensity profile consistent with the lowest-order spatial mode created by a point source as opposed to the square flat-top beam that would otherwise be measured. The wavefront measurement nicely shows the ‘hole’ in the lens from the first down-collimating optic as well as some spherical aberration. This measurement was saved as a reference and will be subtracted from any future measurement.
As a first test of the AO system, it was decided to compensate any existing static aberrations in the ZBL train using the ![]() $1\unicode[STIX]{x1D714}$ CW alignment beam. Figure 17 shows a screenshot of the wavefront measurement (including a measured FF inset) for a cold amplifier beam train.
$1\unicode[STIX]{x1D714}$ CW alignment beam. Figure 17 shows a screenshot of the wavefront measurement (including a measured FF inset) for a cold amplifier beam train.

Figure 17. Phasics software screenshot of ![]() $1\unicode[STIX]{x1D714}$ cw alignment beam passing through a cold amplifier beam train. The inset on the upper left shows the
$1\unicode[STIX]{x1D714}$ cw alignment beam passing through a cold amplifier beam train. The inset on the upper left shows the ![]() $1\unicode[STIX]{x1D714}$ FF measured in the diagnostic box on the mezzanine.
$1\unicode[STIX]{x1D714}$ FF measured in the diagnostic box on the mezzanine.
The peak to valley (PV) wavefront deviation is 2.5 waves with a root mean square (RMS) deviation of 0.45 waves. The calculated FF is in qualitative agreement with the measured FF showing a Strehl ratio of 0.09. This Strehl ratio is far below 0.8 which is typically considered near diffraction limited focus quality. One can also see the applied mirror voltages corresponding to a flat DFM setting. Figure 18 is a screenshot of the wavefront measurement (including an FF inset) for static aberration corrected cold amplifier beam train. The PV wavefront deviation is now only 1.1 waves with an RMS deviation of 0.1 waves. The calculated FF is in good agreement with the measured FF showing a Strehl ratio of 0.7 which is far closer to the desired value of 0.8. One can also see how the applied mirror voltages have changed going from a flat setting (right) to a static corrected setting (left).

Figure 18. Phasics software screenshot of ![]() $1\unicode[STIX]{x1D714}$ cw alignment beam passing through a static aberration corrected cold amplifier beam train. The inset on the upper left shows the
$1\unicode[STIX]{x1D714}$ cw alignment beam passing through a static aberration corrected cold amplifier beam train. The inset on the upper left shows the ![]() $1\unicode[STIX]{x1D714}$ FF measured in the diagnostic box on the mezzanine. Note that the filter and gain settings on the FF camera are the some for both insets.
$1\unicode[STIX]{x1D714}$ FF measured in the diagnostic box on the mezzanine. Note that the filter and gain settings on the FF camera are the some for both insets.
Following the successful correction of static aberration, we then attempted the pre-correction of prompt on-shot aberrations in the amplifier chain. This requires taking a set of uncompensated full system shot wavefront measurements (see Figure 19) with the assumption that the aberrations are not going to change much from shot to shot. Obviously this assumption is not quite correct and the ability to compensate for prompt aberrations will depend largely on the shot to shot repeatability.

Figure 19. Phasics software screenshot of an uncorrected full system shot.
PV and RMS aberrations are of the order of 4.9 waves and 0.9 waves, Respectively, with a corresponding Strehl ratio of 0.05. In order to correct for prompt aberrations one has to invert the measured wavefront and drive the DFM to that shape while compensating for the static aberrations as well. Figure 20 shows a measured full system shot wavefront that was corrected for residual thermal distortions (from previous shots that day), static aberrations, as well as pre-corrected for prompt aberrations at the same time.

Figure 20. Phasics software screenshot of a pre-corrected full system shot.
We achieved a PV of 1.4 waves, an RMS of 0.19 waves and an associated Strehl ratio of 0.3. This is a more than three times increase in focusability and hence about an order of magnitude increase in on target intensity. Recently, we have identified two 12 cm diameter half-wave plates as the main source of our static aberrations and have since then replaced them. This will further improve the beam focal quality in the future.
6 Conclusions
We have presented a brief introduction to the MagLIF concept and how it has prompted new requirements for our high energy lasers. As a result, ZBL was upgraded to twice its previous energy (4 kJ at 527 nm) and its focal spot performance was greatly improved. ZPW has been modified to operate in a long-pulse mode and is now being co-injected into the ZBL beamline. This will make it a versatile tool for MagLIF, backlighting, and high intensity laser plasma interactions.
Acknowledgements
Sandia National Laboratories is a multi-mission laboratory managed and operated by Sandia Corporation, a wholly owned subsidiary of Lockheed Martin Corporation, for the U.S. Department of Energy’s National Nuclear Security Administration under contract DE-AC04-94AL85000.

























