1 Introduction
The quantum description of a classically oscillating electromagnetic field[Reference Glauber1, Reference Glauber2] changed the course of the history on light technology and light–matter interaction, opening the way for the development of quantum optics which has led to countless applications in quantum technology[Reference Acín, Bloch, Buhrman, Calarco, Eichler, Eisert, Esteve, Gisin, Glaser and Jelezko3, Reference Walmsley4]. The nonclassical light sources[Reference Schnabel5–Reference Scully and Zubairy11] have a vital role in this research domain, as they offer a unique resource for fundamental studies and applications in quantum technology. Despite the tremendous progress of this research domain, the majority of the achievements have been accomplished using relatively weak electromagnetic fields (low photon number light sources). Consequently, the applicability of the majority of the existing nonclassical sources is limited by their low intensity while the development of new schemes for the generation of high-intensity nonclassical light is considered as a challenging task. It is practically impossible to address in a single article the countless applications in basic research and technology that can be conducted using sources delivering high photon flux nonclassical light. For this reason, in this perspective article, after a brief introduction on the fundamentals of quantum optics and the generation of nonclassical light, we focus our discussion on the effect of the photon statistics of the light source in nonlinear optics emphasizing on multiphoton excitation processes.
2 Scientific background: classical and nonclassical light
Quantum optics is founded on the quantization of the electromagnetic radiation and the quantum description of a classically oscillating current (coherent states). A key aspect of the studies in this research domain is the measurement and interpretation of light intensity fluctuations and the characterization of the quantum states of light. These are typically achieved by means of photon statistics measurements, phase sensitive homodyne detection schemes such as quantum tomography[Reference Breitennbach, Schiller and Mlynek7, Reference Yuen and Chan8] and measurements of the Glauber correlation functions[Reference Glauber12–Reference Garry and Knight16]. Nonclassical, or quantum, light states, are the light states where the electromagnetic field cannot be described by the classical wave mechanics. Such are, for example, the states of squeezed light, the photon number states, and the cat states. Some of the most useful criteria to distinguish the classical from the nonclassical light are based on the measurement of the (i) Glauber correlation functions ![]() ${g}^{(q)}\left(\tau \right)$, typically obtained by
${g}^{(q)}\left(\tau \right)$, typically obtained by ![]() $q$th-order autocorrelation measurements, with
$q$th-order autocorrelation measurements, with ![]() $q$ being the order of nonlinearity and
$q$ being the order of nonlinearity and ![]() $\tau$ the time delay between the signals, (ii) Wigner function (Q- or P-functions) in phase space[Reference Schleich17], and (iii) photon number distribution, which can be obtained from the Wigner function or directly by photon statistics measurements. As it is nicely described in the book chapter of Strekalov and Lechs (see Ref. [Reference Strekalov and Leuchs18] and references therein), each of the criteria alone is sufficient but not necessary to distinguish classical from nonclassical light.
$\tau$ the time delay between the signals, (ii) Wigner function (Q- or P-functions) in phase space[Reference Schleich17], and (iii) photon number distribution, which can be obtained from the Wigner function or directly by photon statistics measurements. As it is nicely described in the book chapter of Strekalov and Lechs (see Ref. [Reference Strekalov and Leuchs18] and references therein), each of the criteria alone is sufficient but not necessary to distinguish classical from nonclassical light.
Regarding the statistical properties of light, there are several considerations to be taken into account. (i) A coherent state depicts a Poissonian photon number distribution with a normalized ![]() ${g}^{(2)}=1$. This refers to the case where photons randomly reach a detector. (ii) A nonclassical light with super-Poissonian photon number distribution and
${g}^{(2)}=1$. This refers to the case where photons randomly reach a detector. (ii) A nonclassical light with super-Poissonian photon number distribution and ![]() ${g}^{(2)}(0)\,{>}\,1$, is characterized as photon bunching. This refers to the case where the photons have the tendency to reach the detector in bunches, i.e., more close in space (time) than the photons of the coherent state. Chaotic, thermal, or stochastic light, although considered as classical, also corresponds to this case (with the photon number fluctuations to be determined by the coherence time of the light source). (iii) A nonclassical light with sub-Poissonian photon number distribution and
${g}^{(2)}(0)\,{>}\,1$, is characterized as photon bunching. This refers to the case where the photons have the tendency to reach the detector in bunches, i.e., more close in space (time) than the photons of the coherent state. Chaotic, thermal, or stochastic light, although considered as classical, also corresponds to this case (with the photon number fluctuations to be determined by the coherence time of the light source). (iii) A nonclassical light with sub-Poissonian photon number distribution and ![]() $0<{g}^{(2)}(0)<1$, is characterized as photon antibunching. This is a purely quantum effect which refers to the case where the photons have the tendency to reach the detector more equally and further away in space (time) than those of a coherent state. However, in the present article, we consider as nonclassical the light states having a Wigner function that depicts negative values and/or non-Gaussian distributions, and a photon number distribution that deviates from the corresponding of a coherent state that is considered as the best quantum description of a classically oscillating field.
$0<{g}^{(2)}(0)<1$, is characterized as photon antibunching. This is a purely quantum effect which refers to the case where the photons have the tendency to reach the detector more equally and further away in space (time) than those of a coherent state. However, in the present article, we consider as nonclassical the light states having a Wigner function that depicts negative values and/or non-Gaussian distributions, and a photon number distribution that deviates from the corresponding of a coherent state that is considered as the best quantum description of a classically oscillating field.
In particular, a coherent light state is a quantum state of the field that describes the classical behavior of the electromagnetic radiation typically produced by a conventional continuous wave (CW) or pulsed laser system. In this state, the quantum fluctuations of the quadrature components (which are equal to the fluctuations of the vacuum state and randomly distributed in the quadrature components) are equal and the uncertainty of their product is the minimum given by the Heisenberg relation. For a coherent light state, as is considered the light state of a laser field, the electric field variance ![]() $\Delta E$ remains constant within its cycle. An important measurable feature of a light source is its photon number distribution
$\Delta E$ remains constant within its cycle. An important measurable feature of a light source is its photon number distribution ![]() ${P}_n$, resulted by the projection of the light state to the photon number state
${P}_n$, resulted by the projection of the light state to the photon number state ![]() $\mid n\rangle$. For coherent light states
$\mid n\rangle$. For coherent light states ![]() $\mid \alpha \rangle$ this distribution is Poissonian,
$\mid \alpha \rangle$ this distribution is Poissonian,
 $$\begin{align*}{P}_n={\left|\left\langle n|\alpha \right\rangle \right|}^2=\frac{< n{>}^n}{n!}{e}^{-< n >},\end{align*}$$
$$\begin{align*}{P}_n={\left|\left\langle n|\alpha \right\rangle \right|}^2=\frac{< n{>}^n}{n!}{e}^{-< n >},\end{align*}$$and for high mean photon numbers it can be approximated by a Gaussian,
 $$\begin{align*}{P}_n\approx \frac{1}{2\pi {N}_0}\exp \left[\frac{{\left(n-{N}_0\right)}^2}{2{N}_0}\right],\end{align*}$$
$$\begin{align*}{P}_n\approx \frac{1}{2\pi {N}_0}\exp \left[\frac{{\left(n-{N}_0\right)}^2}{2{N}_0}\right],\end{align*}$$where ![]() ${N}_0$ is the mean photon number of the field. In addition, the Wigner function
${N}_0$ is the mean photon number of the field. In addition, the Wigner function
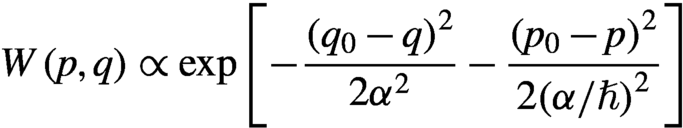
depicts a Gaussian distribution in phase space (where ![]() $q$,
$q$, ![]() $p$ are the field quadratures and
$p$ are the field quadratures and ![]() $\alpha$ the width of the distribution in
$\alpha$ the width of the distribution in ![]() $q$) and a second-order Glauber correlation function
$q$) and a second-order Glauber correlation function ![]() ${g}^{(2)}(0)=1$.
${g}^{(2)}(0)=1$.
A good example of nonclassical light states is the well-known and extensively studied squeezed light states. These are a special class of quantum states where the quantum noise is not randomly distributed between the field quadratures. It is reduced in one of the quadrature components and increased in the other. In this case, the variance of the field quadratures is modulated within the cycle of the field. The photon statistics of these nonclassical light sources significantly deviates from the Poissonian of the coherent states and the Wigner function depicts a distribution that significantly deviates from the Gaussian. Other well-known examples of nonclassical light are the photon number states (or Fock states) and the ‘cat’ states (see Ref. [Reference Strekalov and Leuchs18] and references therein). One of the main characteristics of these light states is that their Wigner function, despite its non-Gaussian form, depicts negative values.
3 Sources of nonclassical light
Nowadays, the nonclassical light states are usually produced by parametric down/up-conversion methods in solids, Kerr effects in optical fibers, semiconductor lasers, wave-mixing processes in atomic ensembles, etc.[Reference Strekalov and Leuchs18, Reference Andersen, Gehring, Marquardt and Leuchs19] and/or by implementing light engineering protocols having as recourses the squeezed, photon number states, and detection approaches[Reference Ourjoumtsev, Jeong, Tualle-Brouri and Grangier20–25]. Although, these sources typically deliver low photon number nonclassical light, recent developments have shown that high-gain parametric down conversion processes can be used for the generation of high photon number squeezed light states[Reference Perez, Spasibko, Sharapova, Tikhonova, Leuchs and Chekhova26–Reference Spasibko, Kopylov, Krutyanskiy, Murzina, Leuchs and Chekhova28]. In addition, in the last few years the fully quantized description of the strong field laser–matter interaction, which takes into account the back action of the interaction on the coherent state of the driving field, has attracted a considerable interest from the theoretical[Reference Gonoskov, Tsatrafyllis, Kominis and Tzallas29–Reference Gorlach, Neufeld, Rivera, Cohen and Kaminer31] and experimental[Reference Tsatrafyllis, Kominis, Gonoskov and Tzallas32, Reference Tsatrafyllis, Khn, Dumergue, Foldi, Kahaly, Cormier, Gonoskov, Kiss, Varju, Varro and Tzallas33] point of view, with the very recent investigation of Ref. [Reference Lewenstein, Ciappina, Pisanty, Rivera-Dean, Lamprou and Tzallas34], to demonstrate in a rigorous way that strongly laser-driven materials can be used for the generation of unique nonclassical light states with controllable features. Taking into account that these sources are driven by intense laser pulses[Reference Mourou35] capable of inducing interactions in the moderate and relativistic regime[Reference Burnett, Baldis, Richardson and Enright36–Reference Thaury and Quéré38] makes them a very promising candidate for the generation of intense nonclassical light.
4 Photon statistics effects in nonlinear optics
Multiphoton processes are the essence of nonlinear optics with countless applications in basic research and technology. This cannot be better outlined than the way that is done using the sentence ‘At this point, one may raise a question: are all media basically nonlinear? The answer is yes. Even in the case of vacuum, photons can interact through vacuum polarization. The nonlinearity is, however, so small that with currently available light sources…’ in the introduction of Shen’s book Principles of Nonlinear Optics [Reference Shen39]. Harmonic generation[25, Reference Shen39, Reference Franken, Hill, Peters and Weinreich40], high harmonic generation in moderate[Reference McPherson, Gibson, Jara, Johann, Luk, McIntyre, Boyer and Rhodes41–Reference Heyl, Arnold, Couairon and L’Huillier43] and relativistic intensity regimes[Reference Mourou35–Reference Thaury and Quéré38], multiphoton processes in atoms[Reference Delone and Krainov44], polymerization[25, Reference Shen39], vacuum polarization in super-relativistic intensities[Reference Mourou35, Reference Mukamel45–Reference Tommasini, Novoa and Roso47], visual science[25, Reference Min, Freudiger, Lu and Xie48], etc. are some examples illustrating the importance of nonlinear optics in different research directions of basic research and technology. Eventually the observation of the nonlinear effects requires driving forces that can efficiently induce nonlinear processes up to the level of observation by the available detection systems. In case that the driving force is induced by an electromagnetic field, nonlinear processes can be observed by increasing the photon flux as well as the quantum fluctuations of the electromagnetic field.
For coherent light states, this is shown by the dependence of the transition rate ![]() $W$ of a qth-order multiphoton process that is proportional to the qth power of the driving field intensity, i.e.,
$W$ of a qth-order multiphoton process that is proportional to the qth power of the driving field intensity, i.e., ![]() $W\propto {F}^q$ (where
$W\propto {F}^q$ (where ![]() $F$ is the photon flux of the driving field). However, the complete relation which includes the photon fluctuations of a light source is
$F$ is the photon flux of the driving field). However, the complete relation which includes the photon fluctuations of a light source is ![]() $W\propto {g}^{(q)}{F}^q$, where
$W\propto {g}^{(q)}{F}^q$, where ![]() ${g}^{(q)}$ is the qth-order Glauber functions with
${g}^{(q)}$ is the qth-order Glauber functions with  $\left\langle :{n}^q:\right\rangle \equiv \left\langle {\left({a}^{\dagger}\right)}^q{a}^q\right\rangle$,
$\left\langle :{n}^q:\right\rangle \equiv \left\langle {\left({a}^{\dagger}\right)}^q{a}^q\right\rangle$, ![]() $n$ is the photon number incident reaching the detector,
$n$ is the photon number incident reaching the detector, ![]() $\left\langle n\right\rangle$ is the average photon number (time integrated) reaching the detector,
$\left\langle n\right\rangle$ is the average photon number (time integrated) reaching the detector, ![]() $F=\left\langle n\right\rangle$ is the mean photon number or photon flux, and
$F=\left\langle n\right\rangle$ is the mean photon number or photon flux, and ![]() ${a}^{\dagger }$,
${a}^{\dagger }$, ![]() $a$ the photon creation and annihilation operators, respectively. Evidently, the photon statistics of a light source, which appears in the
$a$ the photon creation and annihilation operators, respectively. Evidently, the photon statistics of a light source, which appears in the ![]() ${g}^{(q)}$ functions, can dramatically influence the
${g}^{(q)}$ functions, can dramatically influence the ![]() $q$-photon transition rates of a multiphoton process[25, Reference Min, Freudiger, Lu and Xie48–Reference Jechow, Seefeldt, Kurzke, Heuer and Menzel61] simply because any nonlinear effect with ultrashort response time will experience the high/low and ultrafast/slow fluctuating photon numbers (photon bunching/antibunching). This remarkable effect, has tremendous advantages in nonlinear optics. For example, while for a coherent light state
$q$-photon transition rates of a multiphoton process[25, Reference Min, Freudiger, Lu and Xie48–Reference Jechow, Seefeldt, Kurzke, Heuer and Menzel61] simply because any nonlinear effect with ultrashort response time will experience the high/low and ultrafast/slow fluctuating photon numbers (photon bunching/antibunching). This remarkable effect, has tremendous advantages in nonlinear optics. For example, while for a coherent light state ![]() ${g}^{(q)}=1$, the corresponding functions of a chaotic and vacuum squeezed state are
${g}^{(q)}=1$, the corresponding functions of a chaotic and vacuum squeezed state are ![]() ${g}^{(q)}=q!$ and
${g}^{(q)}=q!$ and ![]() ${g}^{(q)}=\left(2q-1\right)!!$ , respectively (Figure 1).
${g}^{(q)}=\left(2q-1\right)!!$ , respectively (Figure 1).
Hence, for the same ![]() $F$, chaotic and nonclassical light states with super-Poissonian photon number distribution can lead to a significant enhancement of the transition rates of highly nonlinear processes compared with those of the coherent light sources (Figure 2).
$F$, chaotic and nonclassical light states with super-Poissonian photon number distribution can lead to a significant enhancement of the transition rates of highly nonlinear processes compared with those of the coherent light sources (Figure 2).
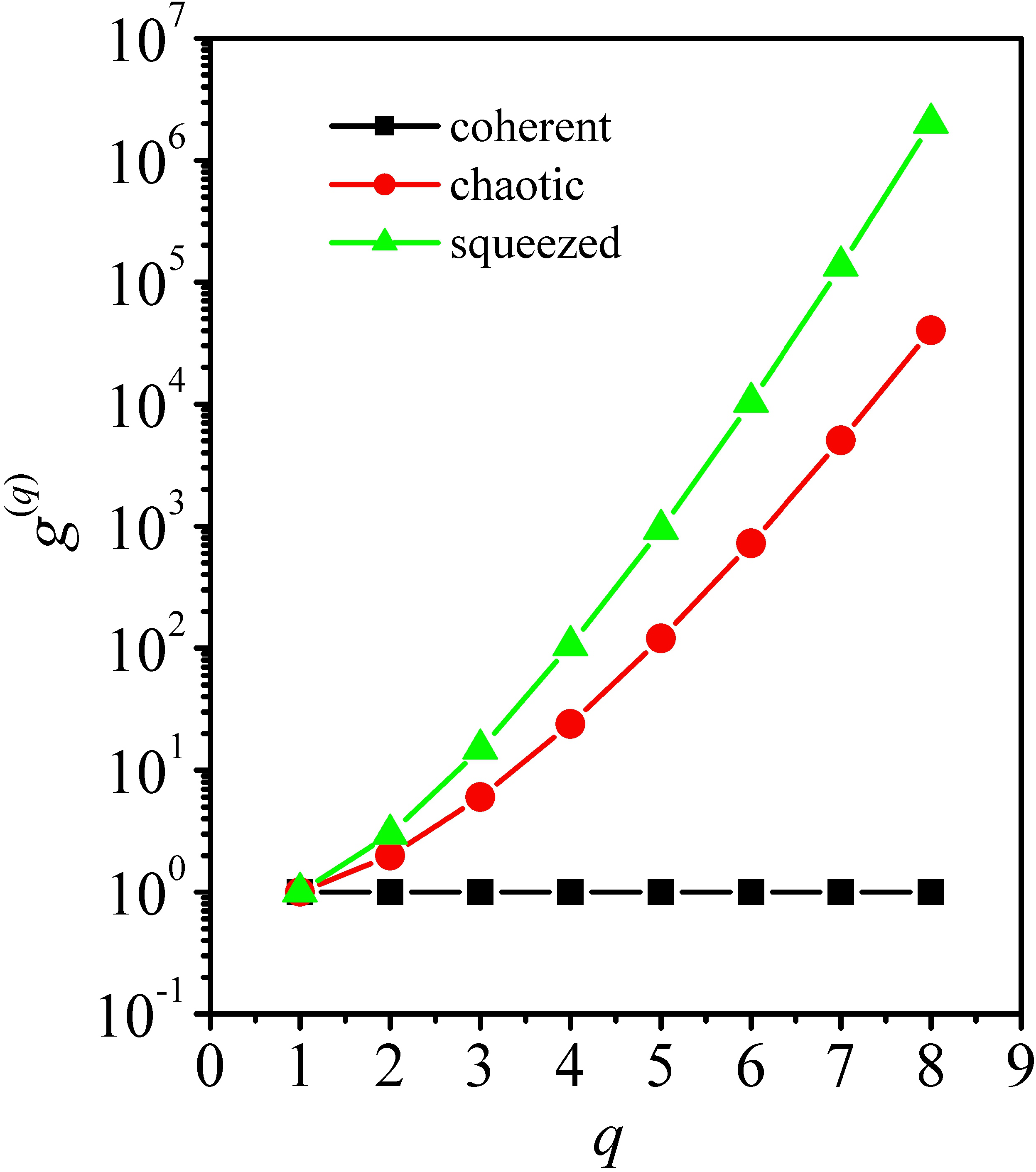
Figure 1 Dependence of ![]() $g$ on the order of nonlinearity
$g$ on the order of nonlinearity ![]() $q$, for coherent (black squares), chaotic (red circles), and squeezed (green triangles) light.
$q$, for coherent (black squares), chaotic (red circles), and squeezed (green triangles) light.
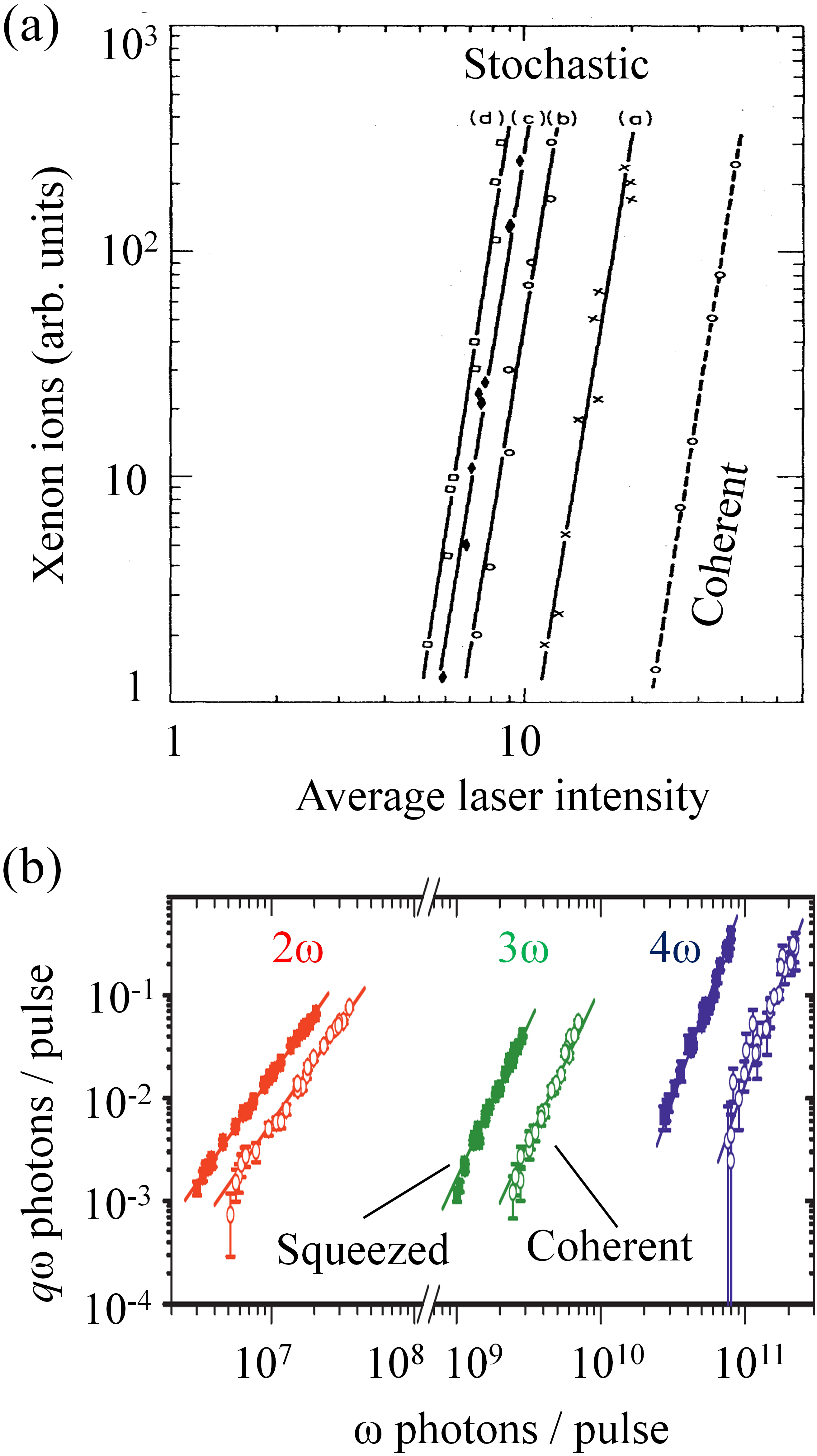
Figure 2 (a) Dependence of the 11-photon multiphoton ionization of Xe on the intensity of a coherent and stochastic light field operating with 10, 30, 70, and 100 phase-unlocked modes (shown with a, b, c, and d in the graph). (b) Dependence of the harmonic yield, produced by nonlinear processes in a crystal, on the intensity of a vacuum squeezed (solid squares) and a coherent (open circles) light states. Parts (a) and (b) are reproduced from Refs. [Reference Lecompte, Mainfray, Manus and Sanchez57] and [Reference Spasibko, Kopylov, Krutyanskiy, Murzina, Leuchs and Chekhova28], respectively.
Evidently, such light sources can also be proved highly beneficial for observing nonlinear processes such as laser-induced pair production or vacuum polarization effects[Reference Mourou35, Reference Salamin, Hu, Hatsagortsyan and Keitel46–Reference Min, Freudiger, Lu and Xie48], which is one of the most challenging tasks in ultrarelativistic interactions. The enhancement of the transition rates was clearly shown using stochastic and vacuum squeezed states. This was achieved by measuring the ion yield produced by multiphoton ionization process of xenon (Figure 2(a))[Reference Lecompte, Mainfray, Manus and Sanchez57] and the harmonic yield produced by nonlinear process in a crystal (Figure 2(b))[Reference Spasibko, Kopylov, Krutyanskiy, Murzina, Leuchs and Chekhova28], respectively. It is noted that, owing to limitations of producing high-intensity thermal light from natural sources, the enhancement of the multiphoton transition rates shown in Figure 2(a), was achieved by mimicking a natural source using stochastic laser pulses generated by an multimode phase unlocked laser system.
The enhancement of the multiphoton transition rates was also studied theoretically and observed experimentally in the XUV spectral region, using FEL sources[Reference Lambropoulos and Nikolopoulos62], whereas the differences compared with the laser-driven coherent XUV sources have been discussed in Ref. [Reference Nayak, Orfanos, Makos, Dumergue, Kühn, Skantzakis, Bodi, Varju, Kalpouzos, Banks, Emmanouilidou, Charalambidis and Tzallas63].
A direct consequence of this enhancement is the ability to study nonlinear processes in all states of matter using light intensities below the damage threshold of the materials. This makes the quantum light a unique resource for studies in visual science, ultrafast science and nonlinear spectroscopy providing the means to observe and control nonlinear processes on a fundamental quantum level. The advantages of using the quantum light towards these directions have been beautifully described in Ref. [Reference Dorfman, Schlawin and Mukamel64]. As is briefly discussed in Ref. [Reference Mukamel, Freyberger, Schleich, Bellini, Zavatta, Leuchs, Silberhorn, Boyd, Sánchez-Soto, Stefanov, Barbieri, Paterova, Krivitsky, Shwartz, Tamasaku, Dorfman, Schlawin, Sandoghdar, Raymer, Marcus, Varnavski, Goodson, Zhou, Shi, Asban, Scully, Agarwal, Peng, Sokolov, Zhang, Zubairy, Vartanyants, del Valle and Laussy65]:
Quantum light offers several advantages to spectroscopy – by enhancing signal strengths, by creating new ‘control knobs’ for the manipulation of optical signals, or by even allowing entirely new types of signals. The strong fluctuations of quantum light can enhance the nonlinear signal strength relative to linear absorption[Reference Schlawin, Dorfman and Mukamel66]. In addition, time-frequency entanglement of photons can be employed to control excitation pathways and excited state populations in aggregates[Reference Schlawin, Dorfman, Fingerhut and Mukamel67]. Third, the quantum nature of light may be used to study collective effects in many-body systems by back and forth projection of entanglement from the field onto the matter. This allows to prepare and control higher excited states in molecular aggregates, and access dark multi-particle states. Finally, photon coincidence counting experiments can access useful material information imprinted on the quantum statistics of emitted light fields.
The most recent example which depicts the impact of the intense quantum light, is demonstrated in the theoretical work of Ref. [Reference Moloudakis and Lambropoulos68] where the authors have shown the influence of the statistical properties of light in atomic spectroscopy and particularly the AC Stark splitting effect.
5 Conclusions
Over the last few decades, tremendous efforts in laser engineering have led to the development of laser systems delivering high-power laser pulses with duration down to 5 fs and power up to the tens of petawatts range. Such systems have been employed in groundbreaking investigations in strong laser field physics[Reference Mourou35]. However, the development and the upgrade of these high-power lasers have mainly been focused on the energy enhancement of the coherent light states of the laser field, leaving unexploited the potential effect that the intense nonclassical or stochastic light sources can have for investigations in nonlinear optics. In this perspective article, we aimed at highlighting the important role that high-power laser systems may play towards the development of intense quantum or stochastic light and its novel applications in nonlinear optics including interactions in the ultrarelativistic regime (such as laser-induced pair production or vacuum polarization effects[Reference Mourou35, Reference Salamin, Hu, Hatsagortsyan and Keitel46–Reference Min, Freudiger, Lu and Xie48]) where the enhancement of the desired signal remains a challenging task. After a brief presentation of the potential schemes that can be used towards this direction, we have discussed the remarkable effects of photon statistics in nonlinear optics.
Acknowledgments
The authors acknowledge LASERLABEUROPE (ECs Seventh Framework Programme, grant number 284464), FORTH Synergy Grant AgiIDA, HELLAS-CH (MIS grant number 5002735), which is implemented under the Action for Strengthening Research and Innovation Infrastructures, funded by the Operational Program Competitiveness, Entrepreneurship and Innovation (NSRF 20142020) and co-financed by Greece and the European Union (European Regional Development Fund), and, finally, the European Unions Horizon 2020 research. ELI-ALPS is supported by the European Union and co-financed by the European Regional Development Fund (GINOP grant number 2.3.6-15-2015-00001).








