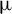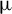1 Introduction
In the past two decades, the study of high-power femtosecond fiber lasers (HPFFLs) has made significant progress thanks to the breakthrough in manufacturing large-mode-area (LMA) fibers, for example, the chirally coupled-core fiber[
Reference Liu, Chang, Litchinitser, Guertin, Jacobsen, Tankala and Galvanauskas
1
] and large-pitch fiber (LPF)[
Reference Limpert, Stutzki, Jansen, Otto, Eidam, Jauregui and Tünnermann
2
]. With the use of LMA fibers it is possible to generate hundreds-of-
![]() $\unicode{x3bc}$
J pulse energy without compromising the beam quality[
Reference Chang and Wei
3
]. Remarkably, a record pulse energy of 2.2 mJ was achieved using LPF at 1.0
$\unicode{x3bc}$
J pulse energy without compromising the beam quality[
Reference Chang and Wei
3
]. Remarkably, a record pulse energy of 2.2 mJ was achieved using LPF at 1.0
![]() $\unicode{x3bc}$
m[
Reference Eidam, Rothhardt, Stutzki, Jansen, Hädrich, Carstens, Jauregui, Limpert and Tünnermann
4
]. By further exploiting the coherent beam combining technique[
Reference Klenke, Muller, Stark, Kienel, Jauregui, Tunnermann and Limpert
5
], an average power of more than 10 kW[
Reference Müller, Aleshire, Klenke, Klenke, Haddad, Légaré, Tünnermann, Tünnermann, Tünnermann and Limpert
6
] and a pulse energy of more than 20 mJ[
Reference Stark, Buldt, Müller, Klenke, Tünnermann and Limpert
7
] have been obtained. In contrast to the great success at 1.0
$\unicode{x3bc}$
m[
Reference Eidam, Rothhardt, Stutzki, Jansen, Hädrich, Carstens, Jauregui, Limpert and Tünnermann
4
]. By further exploiting the coherent beam combining technique[
Reference Klenke, Muller, Stark, Kienel, Jauregui, Tunnermann and Limpert
5
], an average power of more than 10 kW[
Reference Müller, Aleshire, Klenke, Klenke, Haddad, Légaré, Tünnermann, Tünnermann, Tünnermann and Limpert
6
] and a pulse energy of more than 20 mJ[
Reference Stark, Buldt, Müller, Klenke, Tünnermann and Limpert
7
] have been obtained. In contrast to the great success at 1.0
![]() $\unicode{x3bc}$
m, the progress of studying HPFFLs at 1.5
$\unicode{x3bc}$
m, the progress of studying HPFFLs at 1.5
![]() $\unicode{x3bc}$
m is limited, and their performance metrics, particularly the average power and pulse energy, are largely unsatisfying. This can be mainly attributed to the large quantum defect for 980-nm pumping[
Reference Pavlov, Ilbey, Dülgergil, Bayri and Ilday
8
] and technical challenge in fabricating high-gain Er-Yb-doped LMA fibers[
Reference Kuhn, Unger, Jetschke, Kracht, Neumann, Kirchhof and Wessels
9
,
Reference Tankala, Samson, Carter, Farroni, Machewirth, Jacobson, Manyam, Sanchez, Chen, Galvanauskas, Torruellas and Chen
10
]. Frontier applications, however, have a high demand for HPFFLs at 1.5
$\unicode{x3bc}$
m is limited, and their performance metrics, particularly the average power and pulse energy, are largely unsatisfying. This can be mainly attributed to the large quantum defect for 980-nm pumping[
Reference Pavlov, Ilbey, Dülgergil, Bayri and Ilday
8
] and technical challenge in fabricating high-gain Er-Yb-doped LMA fibers[
Reference Kuhn, Unger, Jetschke, Kracht, Neumann, Kirchhof and Wessels
9
,
Reference Tankala, Samson, Carter, Farroni, Machewirth, Jacobson, Manyam, Sanchez, Chen, Galvanauskas, Torruellas and Chen
10
]. Frontier applications, however, have a high demand for HPFFLs at 1.5
![]() $\unicode{x3bc}$
m, for example, high-aspect-ratio through-silicon-vias fabrication[
Reference He, Yu, Tan, Chu, Zhou, Cheng and Sugioka
11
] and corneal surgery[
Reference Plamann, Aptel, Arnold, Courjaud, Crotti, Deloison, Druon, Georges, Hanna, Legeais, Morin, Mottay, Nuzzo, Peyrot and Savoldelli
12
,
Reference Crotti, Deloison, Alahyane, Aptel, Kowalczuk, Legeais, Peyrot, Savoldelli and Plamann
13
]. Moreover, HPFFLs at 1.5
$\unicode{x3bc}$
m, for example, high-aspect-ratio through-silicon-vias fabrication[
Reference He, Yu, Tan, Chu, Zhou, Cheng and Sugioka
11
] and corneal surgery[
Reference Plamann, Aptel, Arnold, Courjaud, Crotti, Deloison, Druon, Georges, Hanna, Legeais, Morin, Mottay, Nuzzo, Peyrot and Savoldelli
12
,
Reference Crotti, Deloison, Alahyane, Aptel, Kowalczuk, Legeais, Peyrot, Savoldelli and Plamann
13
]. Moreover, HPFFLs at 1.5
![]() $\unicode{x3bc}$
m are promising drive sources for frequency conversions through second-harmonic generation[
Reference Jiang, Chen, Yin, Forsberg and He
14
,
Reference Stachowiak, Bogusławski, Głuszek, Łaszczych, Wojtkowski and Soboń
15
], Cherenkov radiation[
Reference Luo, Zhan, Wang, Zhang, Feng and Shen
16
], soliton self-frequency shift (SSFS)[
Reference Nguyen, Kieu, Churin, Ota, Miyawaki and Peyghambarian
17
,
Reference Nicholson, Desantolo, Kaenders and Zach
18
] and self-phase modulation[
Reference Chung, Liu, Cao, Kärtner and Chang
19
], to name just a few. In general, the average-power (or pulse-energy) scaling of the 1.5-
$\unicode{x3bc}$
m are promising drive sources for frequency conversions through second-harmonic generation[
Reference Jiang, Chen, Yin, Forsberg and He
14
,
Reference Stachowiak, Bogusławski, Głuszek, Łaszczych, Wojtkowski and Soboń
15
], Cherenkov radiation[
Reference Luo, Zhan, Wang, Zhang, Feng and Shen
16
], soliton self-frequency shift (SSFS)[
Reference Nguyen, Kieu, Churin, Ota, Miyawaki and Peyghambarian
17
,
Reference Nicholson, Desantolo, Kaenders and Zach
18
] and self-phase modulation[
Reference Chung, Liu, Cao, Kärtner and Chang
19
], to name just a few. In general, the average-power (or pulse-energy) scaling of the 1.5-
![]() $\unicode{x3bc}$
m fs fiber laser is mainly based on chirped pulse amplification (CPA)[
Reference Strickland and Mourou
20
]. A maximum average power of approximately 10 W has been reported for fs pulses at a repetition rate of 100 MHz[
Reference Han, Jang, Kim, Kim and Kim
21
], while mJ pulse energy has been obtained for fs pulses at kHz repetition rates[
Reference Sobon, Kaczmarek, Gluszek, Sotor and Abramski
22
,
Reference Pavlova, Rezaei, Pavlov, Kalaycıoğlu and Ilday
23
]. In most prior schemes, either free-space components[
Reference Elahi, Kalaycıoğlu, Li, Akçaalan and Ilday
24
] or specially designed fibers (e.g., hollow-core photonic crystal fiber[
Reference Wei, Wang, Zhu, Lai, Yan, Ruan, Wang, Sun and Hasan
25
]) were required for the final pulse compression, which however inherently increased their complexity. Inspired by the concept of ablation-cooled material removal technology using GHz-repetition-rate fs pulses[
Reference Audouard, Bonamis, Hönninger and Mottay
26
,
Reference Chen, Lin, Wang, Guan, Wen, Qiao, Wei and Yang
27
], it is of great interest to explore high-power GHz fs fiber lasers for emerging applications requiring fast high-repetition-rate ultrashort pulses. In 2021, a 10.9-W fs all-fiber laser system at 1.5
$\unicode{x3bc}$
m fs fiber laser is mainly based on chirped pulse amplification (CPA)[
Reference Strickland and Mourou
20
]. A maximum average power of approximately 10 W has been reported for fs pulses at a repetition rate of 100 MHz[
Reference Han, Jang, Kim, Kim and Kim
21
], while mJ pulse energy has been obtained for fs pulses at kHz repetition rates[
Reference Sobon, Kaczmarek, Gluszek, Sotor and Abramski
22
,
Reference Pavlova, Rezaei, Pavlov, Kalaycıoğlu and Ilday
23
]. In most prior schemes, either free-space components[
Reference Elahi, Kalaycıoğlu, Li, Akçaalan and Ilday
24
] or specially designed fibers (e.g., hollow-core photonic crystal fiber[
Reference Wei, Wang, Zhu, Lai, Yan, Ruan, Wang, Sun and Hasan
25
]) were required for the final pulse compression, which however inherently increased their complexity. Inspired by the concept of ablation-cooled material removal technology using GHz-repetition-rate fs pulses[
Reference Audouard, Bonamis, Hönninger and Mottay
26
,
Reference Chen, Lin, Wang, Guan, Wen, Qiao, Wei and Yang
27
], it is of great interest to explore high-power GHz fs fiber lasers for emerging applications requiring fast high-repetition-rate ultrashort pulses. In 2021, a 10.9-W fs all-fiber laser system at 1.5
![]() $\unicode{x3bc}$
m with a fundamental repetition rate of 4.9 GHz was reported[
Reference Kuznetsova and Wise
28
], wherein the pulse amplification leveraged the soliton-effect-mediated self-compression process, named nonlinear chirped pulse amplification (NCPA)[
Reference Wu, Liang, Lin, Ling, Zhang, Yang, Wei and Yang
29
], which has been proven to be promising for high-power GHz-repetition-rate fs all-fiber lasers with energy of several to tens of nJ[
Reference Chao, Sander, Chang, Morse, Cox, Petrich, Kolodziejski, Kärtner and Ippen
30
,
Reference Dudley, Genty and Coen
31
].
$\unicode{x3bc}$
m with a fundamental repetition rate of 4.9 GHz was reported[
Reference Kuznetsova and Wise
28
], wherein the pulse amplification leveraged the soliton-effect-mediated self-compression process, named nonlinear chirped pulse amplification (NCPA)[
Reference Wu, Liang, Lin, Ling, Zhang, Yang, Wei and Yang
29
], which has been proven to be promising for high-power GHz-repetition-rate fs all-fiber lasers with energy of several to tens of nJ[
Reference Chao, Sander, Chang, Morse, Cox, Petrich, Kolodziejski, Kärtner and Ippen
30
,
Reference Dudley, Genty and Coen
31
].
To compare the parameter regimes of NCPA systems with those of conventional CPA systems, the typical average power and soliton order N of 1.5-
![]() $\unicode{x3bc}$
m CPA- and NCPA-based HPFFLs are summarized in Figure 1. In contrast to the higher soliton order of CPA systems, that is, typically higher than 100 for long enough dispersion length
$\unicode{x3bc}$
m CPA- and NCPA-based HPFFLs are summarized in Figure 1. In contrast to the higher soliton order of CPA systems, that is, typically higher than 100 for long enough dispersion length
![]() ${L}_{\mathrm{D}}$
, the soliton order of NCPA systems typically ranges between
${L}_{\mathrm{D}}$
, the soliton order of NCPA systems typically ranges between
![]() $N=2$
and
$N=2$
and
![]() $N=16$
, and here it is worth noting that a soliton order of less than 16 is significantly important for preventing severe coherence degradation caused by parametrically amplified intensity noise of the high-power pulse[
Reference Pelusi and Liu
32
]. The definition of the soliton order can be written as follows[
Reference Otto, Stutzki, Jansen, Eidam, Jauregui, Limpert and Tünnermann
33
]:
$N=16$
, and here it is worth noting that a soliton order of less than 16 is significantly important for preventing severe coherence degradation caused by parametrically amplified intensity noise of the high-power pulse[
Reference Pelusi and Liu
32
]. The definition of the soliton order can be written as follows[
Reference Otto, Stutzki, Jansen, Eidam, Jauregui, Limpert and Tünnermann
33
]:
 $$\begin{align}N=\sqrt{\frac{\gamma {P}_{\mathrm{av}}\tau }{3.526\left|{\beta}_2\right|{f}_{\mathrm{R}}}},\end{align}$$
$$\begin{align}N=\sqrt{\frac{\gamma {P}_{\mathrm{av}}\tau }{3.526\left|{\beta}_2\right|{f}_{\mathrm{R}}}},\end{align}$$
where
![]() $\gamma$
is the nonlinear coefficient,
$\gamma$
is the nonlinear coefficient,
![]() ${P}_{\mathrm{av}}$
is the average power,
${P}_{\mathrm{av}}$
is the average power,
![]() $\tau$
is the pulse duration,
$\tau$
is the pulse duration,
![]() ${f}_{\mathrm{R}}$
is the repetition rate and
${f}_{\mathrm{R}}$
is the repetition rate and
![]() ${\beta}_2$
is the group velocity dispersion. By utilizing LMA fibers with a lower nonlinear coefficient and increasing repetition rate, further power scaling of NCPA-HPFFLs at a relatively low soliton-order level could be realized, which is anticipated and depicted by the dashed line in Figure 1. Meanwhile, we admit that pushing the power of 1.5-
${\beta}_2$
is the group velocity dispersion. By utilizing LMA fibers with a lower nonlinear coefficient and increasing repetition rate, further power scaling of NCPA-HPFFLs at a relatively low soliton-order level could be realized, which is anticipated and depicted by the dashed line in Figure 1. Meanwhile, we admit that pushing the power of 1.5-
![]() $\unicode{x3bc}$
m HPFFLs to the 100-W level in all-fiber configurations approaches or even enters the transverse mode instability (TMI) regime (shaded area in Figure 1)[
Reference Jauregui, Stihler and Limpert
34
,
Reference Dudley and Taylor
35
], especially for a relatively large quantum defect for Er-Yb-doped fibers (EYDFs) using a 980-nm pumping scheme.
$\unicode{x3bc}$
m HPFFLs to the 100-W level in all-fiber configurations approaches or even enters the transverse mode instability (TMI) regime (shaded area in Figure 1)[
Reference Jauregui, Stihler and Limpert
34
,
Reference Dudley and Taylor
35
], especially for a relatively large quantum defect for Er-Yb-doped fibers (EYDFs) using a 980-nm pumping scheme.

Figure 1 The average power versus soliton order N of 1.5-
![]() $\unicode{x3bc}$
m high-power ultrafast fiber lasers. Triangles and hexagrams respectively denote CPA- and NCPA-based fiber lasers. A more comprehensive survey of related references is provided in Table 3, Appendix A. The dashed-dotted line and dashed line correspond to a 10-
$\unicode{x3bc}$
m high-power ultrafast fiber lasers. Triangles and hexagrams respectively denote CPA- and NCPA-based fiber lasers. A more comprehensive survey of related references is provided in Table 3, Appendix A. The dashed-dotted line and dashed line correspond to a 10-
![]() $\unicode{x3bc}$
m-core double-cladding fiber laser system (
$\unicode{x3bc}$
m-core double-cladding fiber laser system (
![]() ${f}_{\mathrm{R}}=5\;\mathrm{GHz}$
,
${f}_{\mathrm{R}}=5\;\mathrm{GHz}$
,
![]() $\gamma =1.6\times {10}^{-3}$
) and a 25-
$\gamma =1.6\times {10}^{-3}$
) and a 25-
![]() $\unicode{x3bc}$
m-core large-mode-area fiber laser system (
$\unicode{x3bc}$
m-core large-mode-area fiber laser system (
![]() ${f}_{\mathrm{R}}=10\;\mathrm{GHz}$
,
${f}_{\mathrm{R}}=10\;\mathrm{GHz}$
,
![]() $\gamma =4\times {10}^{-4}$
), respectively (assuming
$\gamma =4\times {10}^{-4}$
), respectively (assuming
![]() $\tau =5\;\mathrm{ps}$
). CPA, chirped pulse amplification; NCPA, nonlinear chirped pulse amplification; TMI, transverse mode instability.
$\tau =5\;\mathrm{ps}$
). CPA, chirped pulse amplification; NCPA, nonlinear chirped pulse amplification; TMI, transverse mode instability.
In this work, we demonstrate a 100-W-class NCPA-based fs laser system at 1.5 µm in an all-fiber configuration by adopting LMA fiber. By leveraging the soliton-effect-based pulse compression effect as well as pre-chirping dispersion management, 239-fs pulses at a repetition rate of 10.6 GHz are generated with a maximum power of 106.4 W – a record value so far. The coherence performance of the high-power GHz fs pulses is evaluated by the spectral fringe visibility measurement, wherein optical spectra with the distinguishable 10.6-GHz longitudinal-mode spacing are recorded. Furthermore, the potential nonlinear interaction among transverse modes LP01, LP11 and LP21 is carefully investigated for high-power amplification using LMA fiber, and the intermodal (IM) modulational instability (MI) is theoretically investigated and experimentally identified.
2 Experimental setup: design and implementation
In this section, we firstly investigate the pulse characteristics in the NCPA system by numerically solving the generalized nonlinear Schrödinger equation (GNLSE). The numerical simulation aims to identify the appropriate range of pre-chirping group delay dispersion (GDD) for optimal pulse compression, based on which the 1.5-
![]() $\unicode{x3bc}$
m 100-W-class GHz fs all-fiber laser system is designed.
$\unicode{x3bc}$
m 100-W-class GHz fs all-fiber laser system is designed.
2.1 Theoretical model of the 100-W-class GHz fs all-fiber laser system at 1.5
 $\mu$
m
$\mu$
m
To characterize the pulse propagation along the LMA fiber used in the main fiber amplifier, the GNLSE is utilized[ Reference Mitschke and Mollenauer 36 ]:
 $$\begin{align} &\frac{\partial A}{\partial z}+i\frac{\beta_2}{2}\frac{\partial^2A}{\partial {t}^2}-\frac{\beta_3}{6}\frac{\partial^3A}{\partial {t}^3}\nonumber\\&\quad= i\gamma \left(1+\frac{i}{\omega_0}\frac{\partial }{\partial t}\right)\left(A\left(z,t\right){\int}_{-\infty}^{\infty }R\left({t}^{\prime}\right){\left|A\left(z,t-{t}^{\prime}\right)\right|}^2\mathrm{d}{t}^{\prime}\right), \nonumber\\&R(t)=\left(1-{f}_{\mathrm{R}}\right)\delta (t)+{f}_{\mathrm{R}}\left({\tau}_1^{-2}+{\tau}_2^{-2}\right){\tau}_1{e}^{-t/{\tau}_2}\sin \left(\frac{t}{\tau_1}\right)H(t),\nonumber\\&A\left(0,t\right)={\mathcal{F}}^{-1}\left(\mathcal{F}\left(\sqrt{P_{\mathrm{p}0}}\operatorname{sech}\left(1.763\frac{t}{\tau_0}\right)\right){e}^{i{\beta}_{\mathrm{PC}}{\omega}^2/2}\right), \end{align}$$
$$\begin{align} &\frac{\partial A}{\partial z}+i\frac{\beta_2}{2}\frac{\partial^2A}{\partial {t}^2}-\frac{\beta_3}{6}\frac{\partial^3A}{\partial {t}^3}\nonumber\\&\quad= i\gamma \left(1+\frac{i}{\omega_0}\frac{\partial }{\partial t}\right)\left(A\left(z,t\right){\int}_{-\infty}^{\infty }R\left({t}^{\prime}\right){\left|A\left(z,t-{t}^{\prime}\right)\right|}^2\mathrm{d}{t}^{\prime}\right), \nonumber\\&R(t)=\left(1-{f}_{\mathrm{R}}\right)\delta (t)+{f}_{\mathrm{R}}\left({\tau}_1^{-2}+{\tau}_2^{-2}\right){\tau}_1{e}^{-t/{\tau}_2}\sin \left(\frac{t}{\tau_1}\right)H(t),\nonumber\\&A\left(0,t\right)={\mathcal{F}}^{-1}\left(\mathcal{F}\left(\sqrt{P_{\mathrm{p}0}}\operatorname{sech}\left(1.763\frac{t}{\tau_0}\right)\right){e}^{i{\beta}_{\mathrm{PC}}{\omega}^2/2}\right), \end{align}$$
where
![]() $A\left(z,t\right)$
is the slowly varying field envelope at a carrier angular frequency
$A\left(z,t\right)$
is the slowly varying field envelope at a carrier angular frequency
![]() ${\omega}_0$
and
${\omega}_0$
and
![]() $R(t)$
accounts for the Raman response, wherein
$R(t)$
accounts for the Raman response, wherein
![]() $\delta (t)$
and
$\delta (t)$
and
![]() $H(t)$
are the Dirac function and Heaviside step function, respectively. The key parameters used in Equation (2) are provided in Table 1. Considering the power variation in the main fiber amplifier, an effective fiber length
$H(t)$
are the Dirac function and Heaviside step function, respectively. The key parameters used in Equation (2) are provided in Table 1. Considering the power variation in the main fiber amplifier, an effective fiber length
![]() ${L}_{\mathrm{eff}}$
in the numerical calculation is defined as follows:
${L}_{\mathrm{eff}}$
in the numerical calculation is defined as follows:
where
![]() ${L}_{\mathrm{LMA}}$
and
${L}_{\mathrm{LMA}}$
and
![]() ${L}_{\mathrm{PF}}$
are the length of the LMA fiber and the matching passive fiber, respectively. To study the coherence degradation, an intensity noise with a fraction of approximately 2% is applied to the input signal
${L}_{\mathrm{PF}}$
are the length of the LMA fiber and the matching passive fiber, respectively. To study the coherence degradation, an intensity noise with a fraction of approximately 2% is applied to the input signal
![]() ${\left|A\left(0,t\right)\right|}^2$
.
${\left|A\left(0,t\right)\right|}^2$
.
Table 1 Key parameters used in the numerical simulation.

By varying the pre-chirping GDD
![]() ${\beta}_{\mathrm{PC}}$
, the optical spectrum, as well as the compressed pulsewidth of the pulse at
${\beta}_{\mathrm{PC}}$
, the optical spectrum, as well as the compressed pulsewidth of the pulse at
![]() $z={L}_{\mathrm{eff}}$
, is visualized and is shown in Figure 2. According to the spectral-temporal characteristics, three distinctive regimes are identified. In regime I for
$z={L}_{\mathrm{eff}}$
, is visualized and is shown in Figure 2. According to the spectral-temporal characteristics, three distinctive regimes are identified. In regime I for
![]() $\left|{\beta}_{\mathrm{PC}}\right|\le 0.25\;{\mathrm{ps}}^2$
, the asymmetric red-shift component clearly identifies the Raman-effect-driven SSFS[
Reference Gordon
37
,
Reference Agrawal
38
], as manifested by the spectral evolution. In this case, appreciable energy transfer to Raman solitons can occur when the length of LMA fiber exceeds the fission distance
$\left|{\beta}_{\mathrm{PC}}\right|\le 0.25\;{\mathrm{ps}}^2$
, the asymmetric red-shift component clearly identifies the Raman-effect-driven SSFS[
Reference Gordon
37
,
Reference Agrawal
38
], as manifested by the spectral evolution. In this case, appreciable energy transfer to Raman solitons can occur when the length of LMA fiber exceeds the fission distance
![]() ${L}_{\mathrm{fiss}}$
[
Reference Pelusi and Liu
32
], which is defined by
${L}_{\mathrm{fiss}}$
[
Reference Pelusi and Liu
32
], which is defined by
![]() ${L}_{\mathrm{fiss}}\sim {L}_{\mathrm{D}}/N\propto \tau /\sqrt{P_{\mathrm{p}}}$
, where
${L}_{\mathrm{fiss}}\sim {L}_{\mathrm{D}}/N\propto \tau /\sqrt{P_{\mathrm{p}}}$
, where
![]() ${L}_{\mathrm{D}}$
is the dispersion length and
${L}_{\mathrm{D}}$
is the dispersion length and
![]() $\tau$
and
$\tau$
and
![]() ${P}_{\mathrm{p}}$
are the pulsewidth and peak power, respectively, with respect to the pre-chirped signal
${P}_{\mathrm{p}}$
are the pulsewidth and peak power, respectively, with respect to the pre-chirped signal
![]() $A\left(0,t\right)$
. From this perspective, the smaller
$A\left(0,t\right)$
. From this perspective, the smaller
![]() ${\beta}_{\mathrm{PC}}$
that results in shorter pulsewidth and higher peak power corresponds to a smaller fission distance
${\beta}_{\mathrm{PC}}$
that results in shorter pulsewidth and higher peak power corresponds to a smaller fission distance
![]() ${L}_{\mathrm{fiss}}$
, indicating a higher possibility of SSFS. In regime III for
${L}_{\mathrm{fiss}}$
, indicating a higher possibility of SSFS. In regime III for
![]() $\left|{\beta}_{\mathrm{PC}}\right|>1\;{\mathrm{ps}}^2$
, the duration of the compressed pulse is broadened to the ps level as a relatively weak nonlinear effect. Specifically, the pulse stretch with larger pre-chirping GDD renders an optimal distance for self-compression
$\left|{\beta}_{\mathrm{PC}}\right|>1\;{\mathrm{ps}}^2$
, the duration of the compressed pulse is broadened to the ps level as a relatively weak nonlinear effect. Specifically, the pulse stretch with larger pre-chirping GDD renders an optimal distance for self-compression
![]() ${L}_{\mathrm{SC}}\sim 0.16\pi {L}_{\mathrm{fiss}}$
[
Reference McFerran, Nenadović, Swann, Schlager and Newbury
39
] that is considerably longer than the length of the LMA fiber.
${L}_{\mathrm{SC}}\sim 0.16\pi {L}_{\mathrm{fiss}}$
[
Reference McFerran, Nenadović, Swann, Schlager and Newbury
39
] that is considerably longer than the length of the LMA fiber.

Figure 2 Numerical simulations of the amplified signals with different pre-chirping group delay dispersions (GDDs). (a) The contour plot of optical spectra with varying pre-chirping dispersion. SSFS, soliton self-frequency shift. (b) The corresponding pulsewidth variation. Regimes I, II and III are designated according to the spectral-temporal characteristics, and the pulse amplifications governed by the Raman effect, the soliton effect and weak nonlinearity, respectively, are identified.
Regime II exhibits higher-order soliton dynamics without the onset of soliton fission (i.e., generation of Raman solitons). In this regime, the pre-chirping GDD imposed upon the pulse leads to a self-compression distance
![]() ${L}_{\mathrm{SC}}$
that fits the length of the LMA fiber, such that the nonlinear spectral broadening occurs before the generation of the Stokes wave resulting from the Raman effect. The design of the NCPA system here must rely on the control of soliton dynamics: on one hand, the pre-chirping GDD should not be too small, otherwise soliton fission occurs and thus generates redshifted Raman solitons with limited spectral coherence; on the other hand, a pre-chirping GDD that is much too large will weaken the nonlinear spectral broadening, and thereby hinder the pulse self-compression. According to the numerical simulation, an appropriate pre-chirping GDD can vary in a range of
${L}_{\mathrm{SC}}$
that fits the length of the LMA fiber, such that the nonlinear spectral broadening occurs before the generation of the Stokes wave resulting from the Raman effect. The design of the NCPA system here must rely on the control of soliton dynamics: on one hand, the pre-chirping GDD should not be too small, otherwise soliton fission occurs and thus generates redshifted Raman solitons with limited spectral coherence; on the other hand, a pre-chirping GDD that is much too large will weaken the nonlinear spectral broadening, and thereby hinder the pulse self-compression. According to the numerical simulation, an appropriate pre-chirping GDD can vary in a range of
![]() $0.25\;{\mathrm{ps}}^2<\left|{\beta}_{\mathrm{PC}}\right|\le 1\;{\mathrm{ps}}^2$
, which corresponds to an adjustable length of 6.2 m when using dispersion-compensation fiber (DCF,
$0.25\;{\mathrm{ps}}^2<\left|{\beta}_{\mathrm{PC}}\right|\le 1\;{\mathrm{ps}}^2$
, which corresponds to an adjustable length of 6.2 m when using dispersion-compensation fiber (DCF,
![]() $\sim$
120 ps2/km dispersion).
$\sim$
120 ps2/km dispersion).
2.2 Experimental setup and implementation details
The experimental setup of the 100-W-class GHz fs all-fiber laser system at 1.5
![]() $\unicode{x3bc}$
m is illustrated in Figure 3. The laser system mainly consists of a Fabry–Pérot fiber oscillator serving as the seed, four stages of fiber pre-amplifiers and a main fiber amplifier using polarization-maintaining LMA (PLMA) fiber.
$\unicode{x3bc}$
m is illustrated in Figure 3. The laser system mainly consists of a Fabry–Pérot fiber oscillator serving as the seed, four stages of fiber pre-amplifiers and a main fiber amplifier using polarization-maintaining LMA (PLMA) fiber.

Figure 3 Schematic diagram of the experimental setup. Dispersion-compensation fiber (DCF) is employed to perform pre-chirping dispersion management. SESAM, semiconductor saturable absorber mirror; DF, dielectric film; EYDF, Er-Yb-doped fiber; PC, polarization controller; WDM, wavelength-division multiplexer; SM-LD, single-mode laser diode; ISO, isolator; EDF, Er-doped fiber; MM-LD, multimode laser diode; SPC, signal-pump combiner; DC-EYDF, double-cladding EYDF; OC, optical coupler; PM-DC-EYDF, polarization-maintaining DC-EYDF; PLMA-DC-EYDF, polarization-maintaining large-mode-area DC-EYDF; QBH, quartz block head; PM, polarization-maintaining.
The ultrashort fiber resonator of the seed laser consists of a 1-cm-long homemade EYDF, a semiconductor saturable-absorber mirror (SESAM, Batop) and a fiber-type dielectric film (DF). The homemade EYDF has a core/cladding diameter of 5.4/127
![]() $\unicode{x3bc}$
m, a numerical aperture of 0.206 at 1.5
$\unicode{x3bc}$
m, a numerical aperture of 0.206 at 1.5
![]() $\unicode{x3bc}$
m and a gain coefficient of 9.13 dB/cm at 1535 nm[Reference McFerran, Nenadović, Swann, Schlager and Newbury39]. The EYDF is pumped by a 974-nm single-mode laser diode (SM-LD, 460 mW maximum power). The EYDF was inserted into a size-matched ceramic ferrule, both end facets of which were perpendicularly polished. The SESAM used for passive mode-locking has an absorbance of 4%, a modulation depth of 3% and a relaxation time of 10 ps. The DF has a high reflectivity of 99.5% at 974 nm and a reflection of 99.2% at 1550–1580 nm, and was directly coated onto a fiber ferrule using a plasma sputter deposition system. The average power of the seed under fundamental mode-locking is about 1.2 mW and the pulsewidth of the seed is estimated to be 2.2 ps. A polarization controller (PC1) is used to adjust the state of polarization and an isolator (ISO) is applied to protect the seed from back reflection. The output of the seed is then fed into the first pre-amplifier, wherein a 2.5-m-long Er-doped fiber (EDF, Coractive Er35-7) is used, pumped by a 974-nm SM-LD (460 mW maximum power). The pre-chirping dispersion, crucial for performing the NCPA system, is implemented by employing different lengths of DCF (YOFC DM1012-D; highlighted by the dashed box in Figure 3), that is, 26, 32 and 38 m, in the experiment. An ISO is placed at the output to prevent back reflection. The loss of fusion splicing between the DCF and standard single-mode fiber (Corning SMF-28e) is approximately 2 dB. The average power after the first pre-amplifier is 15.1 mW. The configuration of the second pre-amplifier is similar to that of the first pre-amplifier, and the average power after the second pre-amplifier is boosted to 160.8 mW. Another PC (PC2) is placed at the output to optimize the state of polarization before entering the polarization-maintaining (PM) parts of the fiber laser system (mainly the fourth pre-amplifier and main fiber amplifier).
$\unicode{x3bc}$
m and a gain coefficient of 9.13 dB/cm at 1535 nm[Reference McFerran, Nenadović, Swann, Schlager and Newbury39]. The EYDF is pumped by a 974-nm single-mode laser diode (SM-LD, 460 mW maximum power). The EYDF was inserted into a size-matched ceramic ferrule, both end facets of which were perpendicularly polished. The SESAM used for passive mode-locking has an absorbance of 4%, a modulation depth of 3% and a relaxation time of 10 ps. The DF has a high reflectivity of 99.5% at 974 nm and a reflection of 99.2% at 1550–1580 nm, and was directly coated onto a fiber ferrule using a plasma sputter deposition system. The average power of the seed under fundamental mode-locking is about 1.2 mW and the pulsewidth of the seed is estimated to be 2.2 ps. A polarization controller (PC1) is used to adjust the state of polarization and an isolator (ISO) is applied to protect the seed from back reflection. The output of the seed is then fed into the first pre-amplifier, wherein a 2.5-m-long Er-doped fiber (EDF, Coractive Er35-7) is used, pumped by a 974-nm SM-LD (460 mW maximum power). The pre-chirping dispersion, crucial for performing the NCPA system, is implemented by employing different lengths of DCF (YOFC DM1012-D; highlighted by the dashed box in Figure 3), that is, 26, 32 and 38 m, in the experiment. An ISO is placed at the output to prevent back reflection. The loss of fusion splicing between the DCF and standard single-mode fiber (Corning SMF-28e) is approximately 2 dB. The average power after the first pre-amplifier is 15.1 mW. The configuration of the second pre-amplifier is similar to that of the first pre-amplifier, and the average power after the second pre-amplifier is boosted to 160.8 mW. Another PC (PC2) is placed at the output to optimize the state of polarization before entering the polarization-maintaining (PM) parts of the fiber laser system (mainly the fourth pre-amplifier and main fiber amplifier).
Further power scaling is realized by using cladding-pump scheme. In the third pre-amplifier, a 3.5-m-long double-cladding EYDF (DC-EYDF, Coractive DCF-EY-10/128H) is utilized as the gain medium, which is forward-pumped by a 974-nm multimode laser diode (MM-LD, BWT, 9 W maximum power) through a (2 + 1) × 1 signal-pump combiner (SPC). The average power measured after the EYDF is 1.6 W. The fourth pre-amplifier has a similar configuration to that of the third pre-amplifier, except for the PM gain fiber and pigtails, that is, 4.5-m-long PM-DC-EYDF (Coractive DCF-EY-10/128-PM) and matched PM-DC fiber. The maximum power of the 974-nm MM-LD in this stage is 27 W. The average power after the fourth pre-amplifier is boosted to 5.8 W at a pump power of 21 W. In the main fiber amplifier, a 4.5-m-long PLMA-DC-EYDF (Nufern PLMA-EYDF-25P/300-HE) is forward-pumped by six 940-nm MM-LDs (Lambda Photonics, 70 W maximum power for each) through a (6 + 1) × 1 PM-SPC. At the end of the PLMA-DC-EYDF, a quartz block head (QBH) is connected for the final output.
The output power of the main fiber amplifier is monitored by a thermal power sensor (Ophir FL1100A-BB-65). The optical spectrum is analyzed by an optical spectrum analyzer (Yokogawa AQ6370D), and the pulsewidth is measured by an autocorrelator (APE pulseCheck USB50). The performance of the seed is quantified using a 12.5-GHz high-speed photodetector (Newport 818-BB-51F), a 20-GHz real-time oscilloscope (Teledyne SDA 820Zi-B) and a 26.5-GHz radio-frequency (RF) signal analyzer (Agilent N9020A).
3 Experimental results and discussion
3.1 Characteristics of the seed
The mode-locking with a fundamental repetition rate of 10.6 GHz has a pump threshold of approximately 90 mW, and the average output power of the signal is about 1.2 mW at a pump power of approximately 110 mW. The optical spectrum centered at 1565 nm has a 3-dB bandwidth of 1.6 nm, as illustrated in Figure 4(a), corresponding to a transform-limited pulsewidth of approximately 1.6 ps (assuming a sech2-pulse shape). The RF spectrum is acquired at a resolution bandwidth (RBW) of 10 Hz, as shown in Figure 4(b), wherein a 10.6-GHz fundamental frequency and an 89-dB signal-to-noise ratio (SNR) are indicated, implying a good short-term mode-locking stability. Over a wider frequency span (i.e., 25 GHz), no sidelobe or satellite peak in the RF domain is observed, as shown in Figure 4(c), confirming a stable operation without polarization rotation[ Reference Lin, Wang, He, Chen, Hu, Guo, Xu, Wei and Yang 40 ]. Such a stationary state of polarization is particularly important for PM-fiber amplifiers[ Reference Engin, Kimpel, Burton, Cao, McIntosh, Storm and Gupta 41 ]. Figure 4(d) presents the oscilloscopic trace of the seed that exhibits good intensity uniformity, wherein a temporal period of 94 ps is indicated, in accordance with the repetition rate of approximately 10.6 GHz. It is worth noting that, limited by the electrical bandwidth (i.e., only 12.5 GHz for the photodiode in this case), the pulse trace exhibits a nearly sinusoidal waveform.

Figure 4 The characterization of the seed. (a) The optical spectrum. (b) The radio-frequency (RF) spectrum measured at a resolution bandwidth (RBW) of 10 Hz. (c) The RF spectrum measured at a 25-GHz span at an RBW of 30 kHz. (d) The oscilloscopic trace. Here, the pulse train at a 10.6-GHz repetition rate is viewed as a sinusoidal waveform due to the limitation of the electrical bandwidth. The inset shows the pulse trace in a wider span of 10
![]() $\unicode{x3bc}$
s.
$\unicode{x3bc}$
s.
3.2 Operation regimes of the 100-W-class GHz fs all-fiber laser system
Through monitoring the pulsewidth at port 2 of the fourth pre-amplifier while changing the length of the DCF, a 26-m-long DCF that corresponds to the zero pre-chirping GDD in this system is identified. Inspired by the result of the numerical simulation, we further prolong the length of the DCF to 32 m (within an adjusting range of ~6.2 m) for self-compressing the pulsewidth to the fs regime. Figure 5(a) presents the output power of the amplified signal as a function of the launched pump power, and a maximum signal power of 106.4 W is obtained at a pump power of 285 W, which is, to the best of our knowledge, the highest power of a fs fiber laser at 1.5
![]() $\unicode{x3bc}$
m. Please note that the average power of the amplified signal was measured after passing through two dichroic mirrors with high reflection at 940 nm and high transmission at 1565 nm. The slope efficiency of the main fiber amplifier is about 36.28%, and 23.21% and 25.38% for the third and fourth pre-amplifiers, respectively. It should be pointed out that although the EYDF has a lower pump absorption at 940 nm (typically, four times lower than that of 974 nm) that may lead to a larger length of gain fiber, the use of a 940-nm pumping strategy can effectively reduce the thermal effect[
Reference Creeden, Pretorius, Limongelli and Setzler
42
] and suppress the amplified spontaneous emission (ASE)[
Reference Agrawal
43
]. The autocorrelation trace, as shown in Figure 5(b), exhibits a pulsewidth of 293 fs, assuming a sech2-pulse shape. There exists a visible pedestal in the autocorrelation trace, a typical feature of the soliton-effect-mediated self-compression process[
Reference Xu, Wei, Ren, Wong and Tsia
44
]. The energy ratio of the central pulse is calculated to be 26.6%.
$\unicode{x3bc}$
m. Please note that the average power of the amplified signal was measured after passing through two dichroic mirrors with high reflection at 940 nm and high transmission at 1565 nm. The slope efficiency of the main fiber amplifier is about 36.28%, and 23.21% and 25.38% for the third and fourth pre-amplifiers, respectively. It should be pointed out that although the EYDF has a lower pump absorption at 940 nm (typically, four times lower than that of 974 nm) that may lead to a larger length of gain fiber, the use of a 940-nm pumping strategy can effectively reduce the thermal effect[
Reference Creeden, Pretorius, Limongelli and Setzler
42
] and suppress the amplified spontaneous emission (ASE)[
Reference Agrawal
43
]. The autocorrelation trace, as shown in Figure 5(b), exhibits a pulsewidth of 293 fs, assuming a sech2-pulse shape. There exists a visible pedestal in the autocorrelation trace, a typical feature of the soliton-effect-mediated self-compression process[
Reference Xu, Wei, Ren, Wong and Tsia
44
]. The energy ratio of the central pulse is calculated to be 26.6%.

Figure 5 (a) The output power of the main fiber amplifier as a function of the pump power. (b) The autocorrelation trace measured at the maximum output power of 106.4 W when using a 32-m-long DCF.
To gain a deeper insight into the self-compression characteristics, we have adopted different lengths of DCF to study the distinctive operation regime predicted in the numerical simulation. For a 26-m-long DCF, the laser system operates in regime I, which approaches the zero pre-chirping GDD. Both the numerical and experimental results confirm the generation of a broadband Stokes wave, as shown in Figures 6(a) and 6(b), respectively. Note that the optical spectrum of Figure 6(b) is recorded at a lower signal power of 80 W to prevent potential Raman scattering in the fiber link. The coherence loss, that is, the orange curve in Figure 6(a), can be identified by the fringe visibility of the spectral modulation imprinted by a longitudinal-mode spacing of 10.6 GHz[Reference Li, Yuan, Kang, Li and Wai45, Reference Tai, Hasegawa and Tomita46]. As shown in the closeup of Figure 6(b), an approximately 4-dB spectral fringe contrast suggests a degraded coherence (~0.43) at the central spectral region of the signal; meanwhile, the spectral fringes become almost invisible for redshifted Stokes components, implying that prominent decoherence occurred.

Figure 6 The operation regimes of the high-power fiber laser system by employing different lengths of DCFs. (a) Thirty simulated optical spectra operated in the Raman-effect-dominated regime (regime I) with different random Raman noise (grey curves), the average simulated optical spectrum (black curve) and the degree of coherence (orange curve). (b) Experimental optical spectrum operated in regime I. The inset shows an approximately 4-dB spectral fringe contrast suggesting a degraded coherence (~0.43) at the central spectral region of the signal. (c) The degree of coherence in the soliton-effect-dominated regime (regime II), wherein the central spectral region of the signal shows a good quality of coherence. (d) Experimental optical spectrum operated in regime II. (e) Experimental optical spectrum and autocorrelation trace operated in the weakly nonlinear regime (regime III). (f) The autocorrelation trace operated in regime III. The less-broadened optical spectrum and ps-level pulsewidth indicate weak nonlinearity that is not sufficient for soliton-effect compression.
By prolonging the DCF to 32 m, the fiber laser system enters regime II, wherein the SSFS is well inhibited, as manifested by the measured optical spectrum shown in Figure 6(d). The spectral broadening governed by the soliton dynamics results in effective pulse compression such that the compressed pulses have a pulsewidth at the sub-300 fs level, as shown in Figure 5(b). The calculated spectral fringe visibility is provided in Figure 6(c), which verifies a relatively good coherence over the spectral range: with regard to the main part of the short-wavelength components, a coherence of approximately 1 is calculated for the center wavelength components, that is, the left-hand panel of Figure 6(c), while a reduced coherence of approximately 0.5 is calculated for the long-wavelength components, that is, the right-hand panel of Figure 6(c), which mainly results from the Raman-effect-assisted MI. More details about the MI influence will be discussed in the next section. Further increasing the DCF length to 38 m results in a pre-chirping GDD of
![]() $\left|{\beta}_{\mathrm{PC}}\right|>1\;{\mathrm{ps}}^2$
, for which the spectral-temporal characteristics are shown in Figures 6(e) and 6(f), and a less-broadened optical spectrum and a ps-level pulsewidth are obtained.
$\left|{\beta}_{\mathrm{PC}}\right|>1\;{\mathrm{ps}}^2$
, for which the spectral-temporal characteristics are shown in Figures 6(e) and 6(f), and a less-broadened optical spectrum and a ps-level pulsewidth are obtained.
3.3 Instability mechanism in the 100-W-class GHz fs all-fiber laser system
The MI is a typical phenomenon in optical fiber, especially in the anomalous dispersion regime[
Reference Agrawal
47
,
Reference Christiansen, Sørensen and Scott
48
], and it can act as a predominant mechanism of spontaneously amplifying the relative intensity noise of the signal through the parametric process, leading to coherence deterioration. In general, the frequency-dependent gain
![]() ${g}_{\mathrm{MI}}\left(\Omega \right)$
of the MI in the optical fiber can be described as follows[
Reference Dupiol, Bendahmane, Krupa, Fatome, Tonello, Fabert, Couderc, Wabnitz and Millot
49
]:
${g}_{\mathrm{MI}}\left(\Omega \right)$
of the MI in the optical fiber can be described as follows[
Reference Dupiol, Bendahmane, Krupa, Fatome, Tonello, Fabert, Couderc, Wabnitz and Millot
49
]:
where
![]() $\Omega$
is the offset frequency relative to the carrier frequency
$\Omega$
is the offset frequency relative to the carrier frequency
![]() ${\omega}_0$
. The LMA gain fiber used in the main fiber amplifier has a core diameter of 25
${\omega}_0$
. The LMA gain fiber used in the main fiber amplifier has a core diameter of 25
![]() $\unicode{x3bc}$
m and a numerical aperture (NA) of 0.1, which is larger than the minimum NA of 0.05 for single-mode guiding, such that it supports high-order modes (HOMs), that is, the LP01, LP11 and LP21 modes as shown in Figure 7(a). As a result, it can associate with IM-MI through cross-phase modulation (XPM)[Reference Li, Leng, Zhou and Chen50, Reference Mondal and Varshney51]. To study the potential IM-MI between the transverse modes, we utilize a coupled nonlinear Schrödinger equation in the formalism of the following:
$\unicode{x3bc}$
m and a numerical aperture (NA) of 0.1, which is larger than the minimum NA of 0.05 for single-mode guiding, such that it supports high-order modes (HOMs), that is, the LP01, LP11 and LP21 modes as shown in Figure 7(a). As a result, it can associate with IM-MI through cross-phase modulation (XPM)[Reference Li, Leng, Zhou and Chen50, Reference Mondal and Varshney51]. To study the potential IM-MI between the transverse modes, we utilize a coupled nonlinear Schrödinger equation in the formalism of the following:
with
 $$\begin{align*}{\gamma}_{pq}=\frac{n_2{\omega}_0}{c}\frac{\iint_{-\infty}^{\infty }{\left|{F}_{{p}}\left(x,y\right)\right|}^2{\left|{F}_q\left(x,y\right)\right|}^2 \mathrm{d}x\mathrm{d}y}{\iint_{-\infty}^{\infty }{\left|{F}_{{p}}\left(x,y\right)\right|}^2 \mathrm{d}x\mathrm{d}y{\iint}_{-\infty}^{\infty }{\left|{F}_q\left(x,y\right)\right|}^2 \mathrm{d}x\mathrm{d}y},\end{align*}$$
$$\begin{align*}{\gamma}_{pq}=\frac{n_2{\omega}_0}{c}\frac{\iint_{-\infty}^{\infty }{\left|{F}_{{p}}\left(x,y\right)\right|}^2{\left|{F}_q\left(x,y\right)\right|}^2 \mathrm{d}x\mathrm{d}y}{\iint_{-\infty}^{\infty }{\left|{F}_{{p}}\left(x,y\right)\right|}^2 \mathrm{d}x\mathrm{d}y{\iint}_{-\infty}^{\infty }{\left|{F}_q\left(x,y\right)\right|}^2 \mathrm{d}x\mathrm{d}y},\end{align*}$$
where
![]() ${A}_1$
and
${A}_1$
and
![]() ${A}_2$
are slowly varying field envelopes with respect to two distinct transverse modes,
${A}_2$
are slowly varying field envelopes with respect to two distinct transverse modes,
![]() ${F}_{{p}}\left(x,y\right)$
describes the transverse field distribution of transverse mode
${F}_{{p}}\left(x,y\right)$
describes the transverse field distribution of transverse mode
![]() $p$
,
$p$
,
![]() ${\gamma}_{pq}$
(
${\gamma}_{pq}$
(
![]() $p,\ q=1,2$
) represents the nonlinear coefficients responsible for nonlinear interaction between transverse modes
$p,\ q=1,2$
) represents the nonlinear coefficients responsible for nonlinear interaction between transverse modes
![]() $p$
and
$p$
and
![]() $q$
,
$q$
,
![]() $c$
is the speed of light and
$c$
is the speed of light and
![]() ${n}_2$
is the nonlinear refractive index. Other key parameters are provided in Table 2. Figure 7(b) illustrates the calculated first- and second-order dispersion curves of different linearly-polarized modes.
${n}_2$
is the nonlinear refractive index. Other key parameters are provided in Table 2. Figure 7(b) illustrates the calculated first- and second-order dispersion curves of different linearly-polarized modes.

Figure 7 The intermodal modulation instability (IM-MI) that potentially existed in the LMA fiber-based main fiber amplifier. (a) The transverse modes supported by the 25-
![]() $\unicode{x3bc}$
m-core LMA gain fiber, that is, LP01, LP11 and LP21 in this case. In the calculation, the refractive index difference between the core and cladding is set to 0.0035. (b) The calculated first- and second-order dispersion curves for different linearly-polarized modes. (c) The optical spectra at the average powers of 80 and 100 W. (d) The calculated gain spectra of MI and IM-MIs resulting from the nonlinear interactions between the LP01–LP11 and LP01–LP21 mode pairs.
$\unicode{x3bc}$
m-core LMA gain fiber, that is, LP01, LP11 and LP21 in this case. In the calculation, the refractive index difference between the core and cladding is set to 0.0035. (b) The calculated first- and second-order dispersion curves for different linearly-polarized modes. (c) The optical spectra at the average powers of 80 and 100 W. (d) The calculated gain spectra of MI and IM-MIs resulting from the nonlinear interactions between the LP01–LP11 and LP01–LP21 mode pairs.
Table 2 Key parameters used for calculating intermodal modulational instability.

a The cross-phase modulation between transverse modes LP11 and LP21 is not considered here.
By applying linear stability analysis on the perturbations adding to the fields of
![]() ${A}_1$
and
${A}_1$
and
![]() ${A}_2$
[
Reference Tzang, Caravaca-Aguirre, Wagner and Piestun
52
], the gain spectrum of the IM-MI can be written as follows:
${A}_2$
[
Reference Tzang, Caravaca-Aguirre, Wagner and Piestun
52
], the gain spectrum of the IM-MI can be written as follows:
 $$\begin{align}&g=\max \left(\mathit{\operatorname{Im}}(K)\right),\nonumber\\&\left({\left(K+\frac{\delta_{12}}{2}\Omega \right)}^2-{\beta}_{21}{\Omega}^2\left({\gamma}_{11}{P}_1+\frac{\beta_{21}{\Omega}^2}{2}\right)\right)\nonumber\\&\times \left({\left(K-\frac{\delta_{12}}{2}\Omega \right)}^2-{\beta}_{22}{\Omega}^2\left({\gamma}_{22}{P}_2+\frac{\beta_{22}{\Omega}^2}{2}\right)\right)\nonumber\\& \quad =4{\gamma_{12}}^2{P}_1{P}_2{\beta}_{21}{\beta}_{22}{\Omega}^4.\end{align}$$
$$\begin{align}&g=\max \left(\mathit{\operatorname{Im}}(K)\right),\nonumber\\&\left({\left(K+\frac{\delta_{12}}{2}\Omega \right)}^2-{\beta}_{21}{\Omega}^2\left({\gamma}_{11}{P}_1+\frac{\beta_{21}{\Omega}^2}{2}\right)\right)\nonumber\\&\times \left({\left(K-\frac{\delta_{12}}{2}\Omega \right)}^2-{\beta}_{22}{\Omega}^2\left({\gamma}_{22}{P}_2+\frac{\beta_{22}{\Omega}^2}{2}\right)\right)\nonumber\\& \quad =4{\gamma_{12}}^2{P}_1{P}_2{\beta}_{21}{\beta}_{22}{\Omega}^4.\end{align}$$
Subsequently, we compare the optical spectra of the amplified signal with the gain spectra of the MI and IM-MIs, as shown in Figures 7(c) and 7(d). There exists a short-wavelength sidelobe for an output power of 100 W, as shown in Figure 7(c), which can be attributed to the IM-MI excited by the LP01–LP11 interaction. According to the experiment, the short-wavelength sidelobe was presented when the average power exceeded 85 W, and its intensity was consistently enhanced with the average power. Meanwhile, the spectral hump could have been produced by the interplay between the MI and IM-MI. Notably, the evidence of the IM-MI elucidates a distinctive mechanism for understanding how the presence of HOMs influences the performance of a high-power GHz fs fiber laser. The stability of most CPA fiber laser systems is sensitive to the onset of the TMI when operating with high average power[
Reference Dudley and Taylor
35
]. The present NCPA-mediated scheme, on the other hand, operates with much lower soliton order N, such that it may only suffer from mode instability dominated by these classic nonlinear effects that mainly relate to the peak power instead of the average power, for example, the IM-MI and intermodal four-wave mixing (IM-FWM)[Reference Koplow, Kliner and Goldberg53]. In contrast to the IM-MI, which mainly experiences nonlinear phase modulation (i.e., XPM), IM-FWM can facilitate energy transfer from the fundamental mode LP01 to HOMs in the phase-matching condition[Reference Tao, Su, Ma, Wang and Zhou54]. Hence, when the LMA gain fiber is not well coiled to suppress the HOMs[Reference Zhang, Xu, Xing, Hou, Chen, Li, Dai, Li, Wang and Liao55–Reference Sobon, Krzempek, Kaczmarek and Abramski57], the LP21 component can be parametrically amplified through the IM-FWM, which thus gives rise to mode instability, as schematically illustrated in Figure 8(a). Due to the existence of modal dispersion and the mode coupling effect, pulses with different group velocities can form a pulse doublet with a temporal separation of
![]() $\Delta t={\delta}_{12}\left({L}_{\mathrm{LMA}}+{L}_{\mathrm{PF}}\right)\sim 17.8\;\mathrm{ps}$
at the output of the main fiber amplifier. For a better understanding, the corresponding autocorrelation trace is also provided on the right-hand side of Figure 8(a). In the experiment, if the LMA gain fiber is handled in an inappropriate manner, such as coiling with a relatively large bend radius, we can observe two kinds of spectral modulation patterns, as shown in Figures 8(b) and 8(c). The dominated spectral modulation pattern corresponds to the longitudinal-mode spacing of approximately 10.6 GHz, as shown in the left-hand panel of Figure 8(c). The second kind of spectral modulation pattern, particularly in the longer wavelength region, mainly results from the spectral signature of the pulse doublet, that is, the right-hand panel of Figure 8(c), wherein a modulation period of 0.46 nm coincides well with the temporal separation
$\Delta t={\delta}_{12}\left({L}_{\mathrm{LMA}}+{L}_{\mathrm{PF}}\right)\sim 17.8\;\mathrm{ps}$
at the output of the main fiber amplifier. For a better understanding, the corresponding autocorrelation trace is also provided on the right-hand side of Figure 8(a). In the experiment, if the LMA gain fiber is handled in an inappropriate manner, such as coiling with a relatively large bend radius, we can observe two kinds of spectral modulation patterns, as shown in Figures 8(b) and 8(c). The dominated spectral modulation pattern corresponds to the longitudinal-mode spacing of approximately 10.6 GHz, as shown in the left-hand panel of Figure 8(c). The second kind of spectral modulation pattern, particularly in the longer wavelength region, mainly results from the spectral signature of the pulse doublet, that is, the right-hand panel of Figure 8(c), wherein a modulation period of 0.46 nm coincides well with the temporal separation
![]() $\Delta t$
of 17.8 ps. Based on the above analysis, the MI/IM-MI and IM-FWM could be the key mechanisms of the instability that potentially exists in the present 100-W-class GHz fs all-fiber laser system.
$\Delta t$
of 17.8 ps. Based on the above analysis, the MI/IM-MI and IM-FWM could be the key mechanisms of the instability that potentially exists in the present 100-W-class GHz fs all-fiber laser system.

Figure 8 The influence of intermodal four-wave mixing (IM-FWM) on the output performance of the high-power fiber laser system. (a) The IM-FWM-mediated energy transfer from transverse mode LP01 to LP21. With the presence of the modal dispersion, the pulses of transverse modes LP01 and LP21 walk off from each other, and form a pulse doublet separated by
![]() $\Delta t$
through the mode coupling. The relevant autocorrelation trace is provided as an inset on the right-hand side. (b) The optical spectrum measured with the maximum output power if an inappropriate coiling scheme is used in the experiment. (c) Closeup of the intrinsic longitudinal mode (left) and spectral structure resulting from the pulse doublet pattern (right).
$\Delta t$
through the mode coupling. The relevant autocorrelation trace is provided as an inset on the right-hand side. (b) The optical spectrum measured with the maximum output power if an inappropriate coiling scheme is used in the experiment. (c) Closeup of the intrinsic longitudinal mode (left) and spectral structure resulting from the pulse doublet pattern (right).
4 Conclusion
In conclusion, we have demonstrated a high-power all-fiber fs laser system at 1.5
![]() $\unicode{x3bc}$
m that can deliver ultrashort pulses at a fundamental repetition rate of 10.63 GHz with an average output power of up to 106.4 W – a record for an all-fiber fs laser operating at 1.5
$\unicode{x3bc}$
m that can deliver ultrashort pulses at a fundamental repetition rate of 10.63 GHz with an average output power of up to 106.4 W – a record for an all-fiber fs laser operating at 1.5
![]() $\unicode{x3bc}$
m. By optimizing the pre-chirping GDD and leveraging the soliton-effect-based pulse compression effect, the amplified pulses are compressed to 239 fs. Furthermore, we have discussed the IM-MI that potentially exists in the few-mode LMA gain fiber. This high-power all-fiber fs laser system is shown to be compact, robust and stable, and thus it is anticipated to be a promising tool for scientific, industrial and medical applications.
$\unicode{x3bc}$
m. By optimizing the pre-chirping GDD and leveraging the soliton-effect-based pulse compression effect, the amplified pulses are compressed to 239 fs. Furthermore, we have discussed the IM-MI that potentially exists in the few-mode LMA gain fiber. This high-power all-fiber fs laser system is shown to be compact, robust and stable, and thus it is anticipated to be a promising tool for scientific, industrial and medical applications.
Appendix A
Parameters of some high-power ultrafast fiber lasers at 1.5
![]() $\unicode{x3bc}$
m are summarized in Table 3.
$\unicode{x3bc}$
m are summarized in Table 3.
Table 3 Comparison of high-power ultrafast fiber lasers at 1.5
![]() $\unicode{x3bc}$
m.
$\unicode{x3bc}$
m.

Acknowledgement
This work was partially supported by NSFC Development of National Major Scientific Research Instrument (61927816), the Introduced Innovative Team Project of Guangdong Pearl River Talents Program (2021ZT09Z109), the Natural Science Foundation of Guangdong Province (2021B1515020074), the Mobility Programme of the Sino-German (M-0296), the Double First Class Initiative (D6211170), the Guangdong Key Research and Development Program (2018B090904003), the National Natural Science Foundation of China (NSFC) (U1609219), the Science and Technology Project of Guangdong (2020B1212060002) and the Key R&D Program of Guangzhou (202007020003).