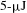1 Introduction
Recent progress of optical parametric chirped-pulse amplifiers (OPCPAs) has realized the generation of intense few-cycle pulses in the IR with stable carrier-envelope phases (CEPs). Using such novel sources, the spectral range of high harmonics was extended from the extreme ultraviolet to the soft-x-ray regions[Reference Popmintchev, Chen, Popmintchev, Arpin, Brown, Ališauskas, Andriukaitis, Balčiunas, Mücke, Pugzlys, Baltuška, Shim, Schrauth, Gaeta, Hernández-García, Plaja, Becker, Jaron-Becker, Murnane and Kapteyn1–Reference Cousin, Silva, Teichmann, Hemmer, Buades and Biegert3]. The CEP dependence of high harmonic cutoffs suggests the generation of attosecond continua that cover the carbon ![]() $K$ edge (
$K$ edge (![]() ${\sim}284$ eV)[Reference Ishii, Kaneshima, Kitano, Kanai, Watanabe and Itatani2, Reference Cousin, Silva, Teichmann, Hemmer, Buades and Biegert3]. The next challenge is to realize time-resolved soft-x-ray absorption spectroscopy of carbon materials with femtosecond to attosecond time resolution. One of the prototypical carbon materials that exhibits ultrafast electronic dynamics is polydiacetylene that has absorption bands in the visible wavelength[Reference Koshihara and Adachi4]. Therefore, it is desirable to establish a method for producing few-femtosecond visible pulses with moderate pulse energy (
${\sim}284$ eV)[Reference Ishii, Kaneshima, Kitano, Kanai, Watanabe and Itatani2, Reference Cousin, Silva, Teichmann, Hemmer, Buades and Biegert3]. The next challenge is to realize time-resolved soft-x-ray absorption spectroscopy of carbon materials with femtosecond to attosecond time resolution. One of the prototypical carbon materials that exhibits ultrafast electronic dynamics is polydiacetylene that has absorption bands in the visible wavelength[Reference Koshihara and Adachi4]. Therefore, it is desirable to establish a method for producing few-femtosecond visible pulses with moderate pulse energy (![]() ${>}1~{\rm\mu}$J), that can be easily integrated into ultrafast intense laser sources for high harmonic generation in the soft x-ray.
${>}1~{\rm\mu}$J), that can be easily integrated into ultrafast intense laser sources for high harmonic generation in the soft x-ray.
For producing ultrashort visible pulses, there are several approaches. The first is a beta-barium borate (BBO)-based noncollinear optical parametric amplifier (NOPA) pumped by the second harmonic of Ti:sapphire lasers[Reference Cerullo, Nisoli, Stagira and De Silvestri5, Reference Shirakawa, Sakane, Takasaka and Kobayashi6]. A typical setup of such a NOPA is usually complicated because it adopts several nonlinear processes, i.e., second-harmonic generation (SHG), white-light generation and parametric amplification. The second is to use self-phase modulation (SPM) in a gas-filled hollow fiber[Reference Nisoli, De Silvestri and Svelto7]. Although the hollow-fiber pulse compression is successfully used for producing intense few-cycle pulses, there are few applications in pump–probe spectroscopy[Reference Matsubara, Ogihara, Itatani, Maeshima, Yonemitsu, Ishikawa, Okimoto, Koshihara, Hiramatsu, Nakano, Yamochi, Saito and Onda8]. It is mainly because the output spectra are less smooth than the output from NOPAs. Furthermore, good pointing stability and short pulse duration (![]() ${<}30$ fs) of the input pulses are necessary for stable and broad output spectra.
${<}30$ fs) of the input pulses are necessary for stable and broad output spectra.
Spectral broadening based on filamentation in a gas-filled cell is an interesting alternative[Reference Corkum, Rolland and Srinivasan-Rao9–Reference Gallmann, Pfeifer, Nagel, Abel, Neumark and Leone12] because of (i) wide and smooth output spectra that cover visible wavelength with an energy of ![]() ${>}1~{\rm\mu}$J, (ii) free-space nonlinear propagation that has spatial filtering effects[Reference Prade, Franco, Mysyrowicz, Couairon, Buersing, Eberle, Krenz, Seiffer and Vasseur13] as well as removing the beam pointing issue, (iii) a wide acceptance range of the input pulse duration up to
${>}1~{\rm\mu}$J, (ii) free-space nonlinear propagation that has spatial filtering effects[Reference Prade, Franco, Mysyrowicz, Couairon, Buersing, Eberle, Krenz, Seiffer and Vasseur13] as well as removing the beam pointing issue, (iii) a wide acceptance range of the input pulse duration up to ![]() ${\sim}100$ fs and (iv) simplicity compared with the NOPA scheme. However, the short-wavelength components of white light produced by filamentation are weaker than the fundamental components around 800 nm by two orders of magnitude. Spectral selection and phase compensation are thus crucial. To solve these problems, we used (i) specially designed band-stop mirrors to block the fundamental wavelength in 720–850 nm, (ii) commercially available broadband dielectric mirrors to select the spectral range in 530–700 nm and (iii) a pair of dispersion compensation mirrors to compress the spectrally filtered pulses down to 6.5 fs.
${\sim}100$ fs and (iv) simplicity compared with the NOPA scheme. However, the short-wavelength components of white light produced by filamentation are weaker than the fundamental components around 800 nm by two orders of magnitude. Spectral selection and phase compensation are thus crucial. To solve these problems, we used (i) specially designed band-stop mirrors to block the fundamental wavelength in 720–850 nm, (ii) commercially available broadband dielectric mirrors to select the spectral range in 530–700 nm and (iii) a pair of dispersion compensation mirrors to compress the spectrally filtered pulses down to 6.5 fs.

Figure 1. Schematic of the experimental setup. Note that the beams are all vertically polarized. The Brewster windows of the gas-filled cell are tilted vertically.

Figure 2. (a) Measured reflectivity and (b) group delay of the band-stop mirror.
2 Experiment
2.1 Filamentation and pulse compression
Figure 1 shows the experimental setup of filamentation and pulse compression. The output pulses from a Ti:sapphire chirped-pulse amplification system (1 mJ, 40 fs, 800 nm) operated at 1 kHz were loosely focused by a lens (![]() $f=1000$ mm) to a 1-m-long gas cell filled with krypton at 1.8 atm. The beam was focused at the center of the cell. Filamentation in the gas cell produced white light that covered from 350 to 2000 nm. We did not observe shorter wavelength components below 350 nm because of the reflectivity cutoff of silver mirrors.
$f=1000$ mm) to a 1-m-long gas cell filled with krypton at 1.8 atm. The beam was focused at the center of the cell. Filamentation in the gas cell produced white light that covered from 350 to 2000 nm. We did not observe shorter wavelength components below 350 nm because of the reflectivity cutoff of silver mirrors.
As shown in Figure 1, we used two kinds of dielectric mirrors for spectral selection and a pair of chirp mirrors for pulse compression. First, the pulses were reflected four times on two near-infrared band-stop mirrors (Tokai Optical Co., Ltd), which were specially designed to suppress the fundamental spectral components in 720–850 nm. Figures 2(a) and (b) show the measured reflectivity and group delay of the band-stop mirror, respectively. The reflectivity was measured with a spectrophotometer (JASCO Co., V-570), and the group delay was measured by a home-built white-light interferometer[Reference Lepetit, Chériaux and Joffre14]. The group delay dispersion is approximately ![]() $-30~\text{fs}^{2}$ at 630 nm. This mirror can efficiently block the fundamental components, while it does not affect the phase of the spectrally broadened components as shown in Figure 2(b).
$-30~\text{fs}^{2}$ at 630 nm. This mirror can efficiently block the fundamental components, while it does not affect the phase of the spectrally broadened components as shown in Figure 2(b).
This band-stop mirror was originally designed for difference frequency generation between the short and long wavelength components after spectral broadening[Reference Ishii, Kaneshima, Kitano, Kanai, Watanabe and Itatani15]. Therefore, it has a high reflectivity range above and below the fundamental wavelength around 800 nm. To separate the spectral components in the visible part around 600 nm from the infrared part reflected by the band-stop mirror, we used two dielectric mirrors (Lattice Electro Optics, Inc., TLM2-600-45). The incoming beam was s-polarized at these mirrors to maximize the reflected bandwidth. In total, four times of reflection on the band-stop mirrors and two times of reflection on the broadband dielectric mirrors were allowed us to select the visible part in 530–700 nm. Dispersion compensation was achieved by five bounces on each of a pair of chirped mirrors (Layertec GmbH, #111346, approximately ![]() $-80~\text{fs}^{2}$ per double bounces at 630 nm). This chirped mirror pair can compensate the dispersion of 1.5-mm-thick fused silica or 2.1-mm-thick calcium fluoride
$-80~\text{fs}^{2}$ per double bounces at 630 nm). This chirped mirror pair can compensate the dispersion of 1.5-mm-thick fused silica or 2.1-mm-thick calcium fluoride ![]() $(\text{CaF}_{\text{2}})$ plates per one round trip. We used a 2-mm
$(\text{CaF}_{\text{2}})$ plates per one round trip. We used a 2-mm ![]() $\text{CaF}_{2}$ plate to control the dispersion by changing the incident angle.
$\text{CaF}_{2}$ plate to control the dispersion by changing the incident angle.

Figure 3. Relative group delays of 1-m-long air (black line), 0.5-mm-thick fused silica (red line) and 0.7-mm-thick ![]() $\text{CaF}_{2}$ (blue dashed line).
$\text{CaF}_{2}$ (blue dashed line).

Figure 4. Results of SHG-FROG measurement. (a), (b) Measured and reconstructed FROG traces, respectively. (c) Retrieved temporal intensity profile (measured: 6.5 fs, transform-limited case: 4.6 fs), (d) Intensity spectrum measured by a spectrometer (black line), retrieved spectrum (red line), and retrieved spectral phase (blue line).
Figure 3 shows the dispersion of 1-m-long air in the standard condition[Reference Ciddor16] that is nearly identical to the dispersion of 0.5-mm-thick fused silica[Reference Malitson17] or 0.7-mm-thick ![]() $\text{CaF}_{\text{2}}$[Reference Li18]. As can be seen in Figure 3, the dispersion of the air would significantly induce phase distortion if the propagation length exceeds
$\text{CaF}_{\text{2}}$[Reference Li18]. As can be seen in Figure 3, the dispersion of the air would significantly induce phase distortion if the propagation length exceeds ![]() ${\sim}0.1$ m. Therefore, we optimized the dispersion of the visible pulses at the point of use by adjusting the number of reflections on the chirped mirrors as well as changing the effective thickness of a fused silica or
${\sim}0.1$ m. Therefore, we optimized the dispersion of the visible pulses at the point of use by adjusting the number of reflections on the chirped mirrors as well as changing the effective thickness of a fused silica or ![]() $\text{CaF}_{\text{2}}$ plate in the beam path.
$\text{CaF}_{\text{2}}$ plate in the beam path.
The compressed pulses were characterized by the SHG-based frequency-resolved optical gating (FROG)[Reference DeLong, Trebino, Hunter and White19, Reference Baltuska, Pshenichnikov and Wiersma20] that employed an 8-![]() ${\rm\mu}$m-thick BBO crystal. We obtained the nearly transform-limited 6.5-fs pulses with a pulse energy of
${\rm\mu}$m-thick BBO crystal. We obtained the nearly transform-limited 6.5-fs pulses with a pulse energy of ![]() $5{\rm\mu}$J and a smooth spectrum in 530–700 nm as shown in Figure 4.
$5{\rm\mu}$J and a smooth spectrum in 530–700 nm as shown in Figure 4.
We inspected the beam quality and pointing stability after the pulse compression. Figures 5(a) and (b) show the beam profiles after pulse compression before and after focusing with a concave mirror (![]() $f=300$ mm), respectively. Because of the spatial filtering effect in filamentation, both of the beam profiles were nearly Gaussian. The
$f=300$ mm), respectively. Because of the spatial filtering effect in filamentation, both of the beam profiles were nearly Gaussian. The ![]() $1/e^{\text{2}}$ intensity beam radii of the near-field beam profile were measured to be 936 and
$1/e^{\text{2}}$ intensity beam radii of the near-field beam profile were measured to be 936 and ![]() $862~{\rm\mu}$m along the horizontal (X) and vertical (Y) directions, respectively, and those of the far-field beam profile were 79 and
$862~{\rm\mu}$m along the horizontal (X) and vertical (Y) directions, respectively, and those of the far-field beam profile were 79 and ![]() $82~{\rm\mu}$m. Pointing stability of the beam before focusing was measured by a quadrant-cell photo-detector. The fluctuation of the beam center with respect to the
$82~{\rm\mu}$m. Pointing stability of the beam before focusing was measured by a quadrant-cell photo-detector. The fluctuation of the beam center with respect to the ![]() $1/e^{\text{2}}$ intensity beam radius was
$1/e^{\text{2}}$ intensity beam radius was ![]() ${\sim}5\times 10^{\text{-3}}$.
${\sim}5\times 10^{\text{-3}}$.

Figure 5. Beam profiles of the compressed pulse (a) before and (b) after focusing with a concave mirror (![]() $f=300$ mm).
$f=300$ mm).

Figure 6. Results of the spectral stability measurement. (a) Averaged spectrum of 1000 single-shot spectra. (b) Standard deviation of each spectral component.
2.2 Spectral stability measurement
We also measured the stability of the spectrum broadened by the filamentation process in a gas-filled cell since shot-to-shot reproducibility is essential for various spectroscopic applications. We put a bandpass filter (Thorlabs, Inc., FESH0700) just behind the gas-filled cell to select the spectral components from 400 to 700 nm, then measured single-shot spectra using a spectrometer (Ocean Optics, Inc., HR2000![]() $+$). Figures 6(a) and (b) show the averaged spectrum over 1000 shots and the standard deviation of each spectral component, respectively. The standard deviation of the pulse energies before filamentation process was measured to be 1.97%. Figure 6(b) shows that the spectral instability of the white light in 420–650 nm was
$+$). Figures 6(a) and (b) show the averaged spectrum over 1000 shots and the standard deviation of each spectral component, respectively. The standard deviation of the pulse energies before filamentation process was measured to be 1.97%. Figure 6(b) shows that the spectral instability of the white light in 420–650 nm was ![]() ${\sim}2\%$, which is similar to the fluctuation of the input pulse energy. The shot-to-shot fluctuation in 650–750 nm is slightly higher than that of 420–650 nm, which was probably due to the SPM in the exit window of the cell. These results show that the white-light continuum produced by filamentation in a gas-filled cell is suitable for spectroscopic applications.
${\sim}2\%$, which is similar to the fluctuation of the input pulse energy. The shot-to-shot fluctuation in 650–750 nm is slightly higher than that of 420–650 nm, which was probably due to the SPM in the exit window of the cell. These results show that the white-light continuum produced by filamentation in a gas-filled cell is suitable for spectroscopic applications.
3 Conclusion
We have produced ![]() $5\text{-}{\rm\mu}\text{J}$, 6.5-fs visible pulses at a repetition rate of 1 kHz using filamentation in a gas cell filled with krypton followed by spectral selection and phase compensation by a combination of dielectric mirrors. The shot-to-shot spectral instability of the visible continuum was measured to be
$5\text{-}{\rm\mu}\text{J}$, 6.5-fs visible pulses at a repetition rate of 1 kHz using filamentation in a gas cell filled with krypton followed by spectral selection and phase compensation by a combination of dielectric mirrors. The shot-to-shot spectral instability of the visible continuum was measured to be ![]() ${\sim}2\%$ (standard deviation) in 420–650 nm, which was almost the same as the energy fluctuation of the output pulses from our Ti:sapphire chirped-pulse amplifier. This pulse compression scheme is simple and robust, and can be easily integrated into intense ultrashort-pulse laser systems. This setup will be used for time-resolved soft-x-ray spectroscopy using high harmonics with sub-10-fs temporal resolution.
${\sim}2\%$ (standard deviation) in 420–650 nm, which was almost the same as the energy fluctuation of the output pulses from our Ti:sapphire chirped-pulse amplifier. This pulse compression scheme is simple and robust, and can be easily integrated into intense ultrashort-pulse laser systems. This setup will be used for time-resolved soft-x-ray spectroscopy using high harmonics with sub-10-fs temporal resolution.
Acknowledgments
This research was partially supported by Grant-in-Aid for Scientific Research (S) Grant Number 23226003, Grant-in-Aid for Young Scientists (B) Grant Number 25790063 and Program for Leading Graduate Schools (MERIT) by Japan Society for the Promotion of Science.