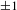1 Introduction
Owing to their helical wavefront structure, beams carrying orbital angular momentum (OAM) have many special characteristics and have been significantly developed and widely used since the first proposal in 1992[Reference Allen, Beijersbergen, Spreeuw and Woerdman1]. As the mode states with discrete ‘twisting’ rates of the spiral phase are mutually orthogonal, the OAM beams exhibit unique advantages in increasing the capacity of optical communication systems[Reference Willner, Huang, Yan, Ren, Ahmed, Xie, Bao, Li, Cao, Zhao, Wang, Lavery, Tur, Ramachandran, Molisch, Ashrafi and Ashrafi2, Reference Wang, Yang, Fazal, Ahmed, Yan, Huang, Ren, Yue, Dolinar, Tur and Willner3]. Additionally, with the phase singularity at the beam center, beams carrying OAM have a ring-shaped hollow intensity distribution and can be used in super-resolution imaging systems[Reference Fürhapter, Jesacher, Bernet and Ritsch-Marte4, Reference Yao and Padgett5]. Moreover, these beams can be used as optical tweezers to manipulate micro-particles due to their unique light radiation pressure and propagation trajectory[Reference Yao and Padgett5, Reference Arita, Mazilu and Dholakia6]. The OAM beams also exhibit excellent resistance to disturbances when they propagate through a random medium[Reference Gbur and Tyson7, Reference Cheng, Haus and Zhan8]. The advantages mentioned above allow OAM beams to be potentially valuable in many applications, and have encouraged researchers to study and develop them as a priority. To date, OAM beams can be generated experimentally by two means: direct generation in the laser cavity and indirect conversion based on a plane wave using various phase adjustors[Reference Yao and Padgett5]. The phase adjustors can be spatially separate devices (i.e., spatial light modulators (SLMs)[Reference Maurer, Jesacher, Bernet and Ritsch-Marte9],
![]() $q$
-plates[Reference Nagali, Sansoni, Sciarrino, Martini, Marrucci, Piccirillo, Karimi and Santamato10], phase holograms[Reference Mirhosseini, Magaña-Loaiza, Chen, Rodenburg, Malik and Boyd11], cylindrical lens pairs[Reference Beijersbergen, Allen, van der Veen and Woerdman12], digital micro-mirror devices[Reference Mirhosseini, Magaña-Loaiza, Chen, Rodenburg, Malik and Boyd13]) or fiber waveguide devices, such as fiber gratings[Reference Bozinovic, Golowich, Kristensen and Ramachandran14] and fiber fused couplers[Reference Yan, Wang, Zhang, Yang, Fazal, Ahmed, Shamee, Willner, Birnbaum and Dolinar15, Reference Shankar, Abdul Khudus, Gregg, Ramachandran, Srinivasan and Brambilla16]. However, due to the limited power handling capacity of available phase adjustors and challenges (for example, nonlinear optics effects) in the power scaling of single-channel laser beams, the output power of the generated OAM beams is relatively low at present[Reference Chu, Sun, Wang, Lü, Xie and Xu17]. Generally, reported research on the transmission properties of OAM beams has been carried out in the laboratory or based on lossless fiber waveguides[Reference Xie, Li, Ren, Huang, Yan, Ahmed, Zhao, Lavery, Ashrafi, Ashrafi, Bock, Tur, Molisch and Willner18, Reference Bozinovic, Yue, Ren, Tur, Kristensen, Huang, Willner and Ramachandran19]. Most of the communication experiments have had a propagation distance limited to several kilometers[Reference Krenn, Fickler, Fink, Handsteiner, Malik, Scheidl, Ursin and Zeilinger20] until very recently, where a hundred-kilometer-long test over a turbulent atmospheric link was demonstrated[Reference Krenn, Handsteiner, Fink, Fickler, Ursin, Malik and Zeilinger21].
$q$
-plates[Reference Nagali, Sansoni, Sciarrino, Martini, Marrucci, Piccirillo, Karimi and Santamato10], phase holograms[Reference Mirhosseini, Magaña-Loaiza, Chen, Rodenburg, Malik and Boyd11], cylindrical lens pairs[Reference Beijersbergen, Allen, van der Veen and Woerdman12], digital micro-mirror devices[Reference Mirhosseini, Magaña-Loaiza, Chen, Rodenburg, Malik and Boyd13]) or fiber waveguide devices, such as fiber gratings[Reference Bozinovic, Golowich, Kristensen and Ramachandran14] and fiber fused couplers[Reference Yan, Wang, Zhang, Yang, Fazal, Ahmed, Shamee, Willner, Birnbaum and Dolinar15, Reference Shankar, Abdul Khudus, Gregg, Ramachandran, Srinivasan and Brambilla16]. However, due to the limited power handling capacity of available phase adjustors and challenges (for example, nonlinear optics effects) in the power scaling of single-channel laser beams, the output power of the generated OAM beams is relatively low at present[Reference Chu, Sun, Wang, Lü, Xie and Xu17]. Generally, reported research on the transmission properties of OAM beams has been carried out in the laboratory or based on lossless fiber waveguides[Reference Xie, Li, Ren, Huang, Yan, Ahmed, Zhao, Lavery, Ashrafi, Ashrafi, Bock, Tur, Molisch and Willner18, Reference Bozinovic, Yue, Ren, Tur, Kristensen, Huang, Willner and Ramachandran19]. Most of the communication experiments have had a propagation distance limited to several kilometers[Reference Krenn, Fickler, Fink, Handsteiner, Malik, Scheidl, Ursin and Zeilinger20] until very recently, where a hundred-kilometer-long test over a turbulent atmospheric link was demonstrated[Reference Krenn, Handsteiner, Fink, Fickler, Ursin, Malik and Zeilinger21].
None of these aforementioned experimental scenarios employ high-power vortex beams. However, owing to the intrinsic beam spreading (in free space or atmosphere) and power loss that cannot be ignored during propagation, the power of OAM beams generated experimentally is still not scalable for a nontrivial propagation distance, such as satellite-to-ground or space-to-ground distances. Additionally, high-power OAM beams can be utilized in many applications, such as nonlinear frequency conversion processes[Reference Chaitanya, Aadhi, Jabir and Samanta22], stability enhancement of optical solitons when propagating through complicated media which can be used in quantum information cryptography and optical computing[Reference Bigelow, Zerom and Boyd23], laser ablation and materials processing[Reference Hamazaki, Morita, Chujo, Kobayashi, Tanda and Omatsu24] and many other high-energy-physics applications, such as tubular plasma generation[Reference Fan, Parra, Alexeev, Kim, Milchberg, Margolin and Pyatnitskii25].
Due to the importance of high-power OAM beams and the extensive application scenarios, researchers have conducted much research on the generation of high-power OAM beams in recent years, including continuous[Reference Okida, Omatsu, Itoh and Yatagai26–Reference Tuan, Hsieh, Lai, Huang and Chen29] and pulsed[Reference Chard, Shardlow and Damzen30–Reference Volodkin, Choporova, Knyazev, Kulipanov, Pavelyev, Soifer and Vinokurov35] high-power OAM beams, with spectral ranges covering the visible light[Reference Chaitanya, Aadhi, Jabir and Samanta22, Reference Chard, Shardlow and Damzen30, Reference Chaitanya, Jabir and Samanta31], near infrared[Reference Okida, Omatsu, Itoh and Yatagai26–Reference Tuan, Hsieh, Lai, Huang and Chen29, Reference Tanaka, Okida, Miyamoto and Omatsu32–Reference Li, Li, Zhang, Miller, Shori and Johnson34] and terahertz[Reference Volodkin, Choporova, Knyazev, Kulipanov, Pavelyev, Soifer and Vinokurov35] regions. To date, efforts have been made to generate high-power OAM beams through methods including crystal lasers[Reference Okida, Omatsu, Itoh and Yatagai26, Reference Tuan, Hsieh, Lai, Huang and Chen29, Reference Chard, Shardlow and Damzen30, Reference Liu, Zhao, Zhou and Shen33], rod amplifiers[Reference Li, Li, Zhang, Miller, Shori and Johnson34], fiber lasers[Reference Chaitanya, Aadhi, Jabir and Samanta22, Reference Aadhi, Samanta, Kumarm and Ebrahim-Zadeh28, Reference Chaitanya, Jabir and Samanta31] and master oscillator power amplifiers[Reference Kim, Kim and Clarkson27]. At present, the highest powers achieved in OAM beams are almost tens of watts[Reference Kim, Kim and Clarkson27, Reference Chard, Shardlow and Damzen30, Reference Volodkin, Choporova, Knyazev, Kulipanov, Pavelyev, Soifer and Vinokurov35], whereas it is known that these methods cannot realize much higher power (kilowatt scale) OAM beams due to the limitations of nonlinear optical effects and the thermal effects of materials[Reference Chaitanya, Aadhi, Jabir and Samanta22, Reference Okida, Omatsu, Itoh and Yatagai26, Reference Chard, Shardlow and Damzen30, Reference Chaitanya, Jabir and Samanta31]. Therefore, it is imperative to devise alternative techniques to access higher power OAM beams, especially using multiple beams to overcome the limitations of single lasers.
Coherent beam combination (CBC) has been proposed to break through the physical limits for single-channel laser beams[Reference Fan36, Reference Liu, Zhou, Xu, Wang and Ma37]. Using different combining elements, CBC techniques can be divided into two major categories: filled aperture combining and tiled aperture combining[Reference Leshchenko38]. For the tiled aperture CBC system, by locking the phase of the beam array with a difference of integral multiples of
![]() $2\unicode[STIX]{x1D70B}$
, the array beams compose a whole plane-like beam, and the combined laser beam in the far-field has an improved brightness in the central lobe. A few years ago, tiled aperture CBC of a fiber laser array increased the output power to kilowatts with good performance and stable phase-control capability[Reference Yu, Augst, Redmond, Goldizen, Murphy, Sanchez and Fan39]. Analogously, the CBC method can be used for reference in high-power OAM beam generation systems. Different from the constructed plane-like wave in the traditional CBC architecture, the phase of the beam array should be transformed into a vortex-like state by applying a discontinuous stepped piston phase in the high-power OAM beam generation system. In the past few years, researchers have theoretically studied the validity and feasibility of this high-power vortex beam generation method using the CBC technique[Reference Chu, Sun, Wang, Lü, Xie and Xu17, Reference Zhi, Tao, Zhou, Ma, Wu, Wang and Si40, Reference Hou, Zhang, Chang, Ma, Su, Wu, Ma and Zhou41]. So far, an important objective that has not been adequately explored in depth is to experimentally generate a beam carrying OAM based on the coherent beam array combination technique.
$2\unicode[STIX]{x1D70B}$
, the array beams compose a whole plane-like beam, and the combined laser beam in the far-field has an improved brightness in the central lobe. A few years ago, tiled aperture CBC of a fiber laser array increased the output power to kilowatts with good performance and stable phase-control capability[Reference Yu, Augst, Redmond, Goldizen, Murphy, Sanchez and Fan39]. Analogously, the CBC method can be used for reference in high-power OAM beam generation systems. Different from the constructed plane-like wave in the traditional CBC architecture, the phase of the beam array should be transformed into a vortex-like state by applying a discontinuous stepped piston phase in the high-power OAM beam generation system. In the past few years, researchers have theoretically studied the validity and feasibility of this high-power vortex beam generation method using the CBC technique[Reference Chu, Sun, Wang, Lü, Xie and Xu17, Reference Zhi, Tao, Zhou, Ma, Wu, Wang and Si40, Reference Hou, Zhang, Chang, Ma, Su, Wu, Ma and Zhou41]. So far, an important objective that has not been adequately explored in depth is to experimentally generate a beam carrying OAM based on the coherent beam array combination technique.
In this paper, we systematically investigate the generation of beams carrying OAM utilizing the CBC technique of fiber lasers, including their conception, theoretical deduction, detailed implementation and testing methods. To the best of our knowledge, this is the first time that a constructed OAM beam based on CBC of a beam array has been experimentally realized.
2 System concept and model
2.1 Concept of the high-power OAM beam generation system
The basic concepts of general OAM beam generation from a single beam and the novel vortex beam generation system using an array of beams are shown in Figure 1. As shown in Figure 1(a), the input beam is a collimated Gaussian beam with a plane phase and Gaussian intensity distribution. By applying a vortex phase screen, the plane wavefront is modulated to become a spiral phase front. In contrast, the novel OAM beam generation system utilizes an array of beams to simulate a single input Gaussian beam. To accurately approximate a single Gaussian beam, the array beamlets should be coherent with each other and the array should have the same intensity distribution in the radial direction together with zero piston phase differences (or an integer of
![]() $2\unicode[STIX]{x1D70B}$
) within the coherence length of the beamlet. At the same time, the phase modulation applied to each beamlet forms a piston phase array with an equivalent step change between any two adjacent beams that are located at the same distance from the center.
$2\unicode[STIX]{x1D70B}$
) within the coherence length of the beamlet. At the same time, the phase modulation applied to each beamlet forms a piston phase array with an equivalent step change between any two adjacent beams that are located at the same distance from the center.

Figure 1. Schematics of (a) the general OAM beam generation method and (b) the novel OAM beam generation system using the beam array CBC technique.
Due to the piston phase array being finite it cannot represent the ideal smooth vortex phase, and the OAM beam generated from the coherent beam array is different from a single OAM beam. The difference is whether the wave vector rotates in the near-field after phase modulation. As depicted in Figure 1(a), the wavefront of the general OAM beam rotates in a spiral trajectory along the propagation direction (namely the beam carries an OAM immediately after phase modulation). In contrast, the array phases remain unchanged during propagation in the near-field, just as shown in Figure 1(b), which means the beam array carries no OAM. However, with increasing propagation distance, the optical fields of the array beams overlap with each other and the monolithic helical phase front forms gradually. When the array beams propagate to the far-field, the initially separated input beams completely overlap and become perfectly coherent with a vortex phase structure like a single beam. As the input array beams can be treated as a single beam with a phase singularity in the far-field perspective, the intensity distribution will have a hollow shape, which is close to an ideal vortex beam. Moreover, it should be noted that the beam array should not contain the central beam, as the phase cannot be modulated into a vortex structure only by piston phase compensation.
The difficulty in using array beams in OAM beam conversion is to control the array beams with equal phase in real time, because the time-varying dynamic optical phase of each beamlet is influenced by various environmental issues, such as vibration. At present, the active CBC technique using the metric of the central-lobe energy in the far-field has been validated for real-time compensation of the piston phase[Reference Weyrauch, Vorontsov, Carhart, Beresnev, Rostov, Polnau and Liu42, Reference Zhou, Liu, Wang, Ma, Ma and Xu43]. Hence, high-power OAM beam generation can be implemented conceptually by CBC utilizing an active control algorithm.
2.2 Theoretical model and numerical analysis
In this sub-section, we will set up a theoretical model to further illustrate the concept of this novel route for OAM generation and perform numerical calculations to validate its feasibility.
As shown in Figure 2, we assume that the optical wave field at the input plane is composed of
![]() $N_{\text{circle}}$
beams in a circular array with
$N_{\text{circle}}$
beams in a circular array with
![]() $N_{j}$
beams on the
$N_{j}$
beams on the
![]() $j$
th circle. The
$j$
th circle. The
![]() $h$
th vector electric field amplitude located on the
$h$
th vector electric field amplitude located on the
![]() $j$
th circle is defined as
$j$
th circle is defined as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \overrightarrow{U}_{\!\!j,h}(\overrightarrow{\unicode[STIX]{x1D70C}}_{\!\!j,h},t,z=0)\nonumber\\ \displaystyle & & \displaystyle \quad =\overrightarrow{e}_{\!\!j,h}(t)W_{j,h}(\overrightarrow{\unicode[STIX]{x1D70C}}_{\!\!j,h})A_{j,h}(\overrightarrow{\unicode[STIX]{x1D70C}}_{\!\!j,h},t)e^{i\unicode[STIX]{x1D714}_{0}t},\nonumber\\ \displaystyle & & \displaystyle \qquad (j=1,\ldots ,N_{\text{circle}};h=1,\ldots ,N_{j}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \overrightarrow{U}_{\!\!j,h}(\overrightarrow{\unicode[STIX]{x1D70C}}_{\!\!j,h},t,z=0)\nonumber\\ \displaystyle & & \displaystyle \quad =\overrightarrow{e}_{\!\!j,h}(t)W_{j,h}(\overrightarrow{\unicode[STIX]{x1D70C}}_{\!\!j,h})A_{j,h}(\overrightarrow{\unicode[STIX]{x1D70C}}_{\!\!j,h},t)e^{i\unicode[STIX]{x1D714}_{0}t},\nonumber\\ \displaystyle & & \displaystyle \qquad (j=1,\ldots ,N_{\text{circle}};h=1,\ldots ,N_{j}),\end{eqnarray}$$
where
![]() $t$
is the time,
$t$
is the time,
![]() $j$
is the circle number of the beam location, and
$j$
is the circle number of the beam location, and
![]() $h$
represents the beam number on the
$h$
represents the beam number on the
![]() $j$
th circle.
$j$
th circle.
![]() $\overrightarrow{e}_{\!\!j,h}(t)$
is the unit vector describing the polarization state. Functions
$\overrightarrow{e}_{\!\!j,h}(t)$
is the unit vector describing the polarization state. Functions
![]() $W_{j,h}(\overrightarrow{\unicode[STIX]{x1D70C}}_{\!\!j,h})$
and
$W_{j,h}(\overrightarrow{\unicode[STIX]{x1D70C}}_{\!\!j,h})$
and
![]() $A_{j,h}(\overrightarrow{\unicode[STIX]{x1D70C}}_{\!\!j,h},t)$
correspond to the truncation window functions and the complex amplitudes of the beamlets’ optical fields. Here
$A_{j,h}(\overrightarrow{\unicode[STIX]{x1D70C}}_{\!\!j,h},t)$
correspond to the truncation window functions and the complex amplitudes of the beamlets’ optical fields. Here
![]() $\overrightarrow{\unicode[STIX]{x1D70C}}_{\!\!j,h}\equiv \overrightarrow{r}-\overrightarrow{r}_{\!\!j,h}$
is the radius vector with respect to
$\overrightarrow{\unicode[STIX]{x1D70C}}_{\!\!j,h}\equiv \overrightarrow{r}-\overrightarrow{r}_{\!\!j,h}$
is the radius vector with respect to
![]() $\overrightarrow{r}_{\!\!j,h}$
, which represents the center coordinate of the beam, and
$\overrightarrow{r}_{\!\!j,h}$
, which represents the center coordinate of the beam, and
![]() $\overrightarrow{r}$
is the radius vector in the input plane.
$\overrightarrow{r}$
is the radius vector in the input plane.

Figure 2. Schematic of the input array beams.
Beams located at the same distance from the array center (namely, having the same
![]() $j$
) have the same intensity distribution and window function. From the perspective of ideal coherent beam combining, the array beams should be linearly polarized with identical polarization directions. So, the optical electrical field of the beam array can be simplified as
$j$
) have the same intensity distribution and window function. From the perspective of ideal coherent beam combining, the array beams should be linearly polarized with identical polarization directions. So, the optical electrical field of the beam array can be simplified as
After piston phase-locking control, the phase differences at a precise time between the array beams are controlled to be zero or an integer multiple of
![]() $2\unicode[STIX]{x1D70B}$
. Thus, the phase term in Equation (2) is a constant with a value of 1 and can be omitted. Then preset spiral-staircase-like piston phases are applied to the array beams and the optical field is transformed to
$2\unicode[STIX]{x1D70B}$
. Thus, the phase term in Equation (2) is a constant with a value of 1 and can be omitted. Then preset spiral-staircase-like piston phases are applied to the array beams and the optical field is transformed to
where
![]() $\ell$
is an integer counting the number of intertwined helices and refers to the topological charge of the beam.
$\ell$
is an integer counting the number of intertwined helices and refers to the topological charge of the beam.
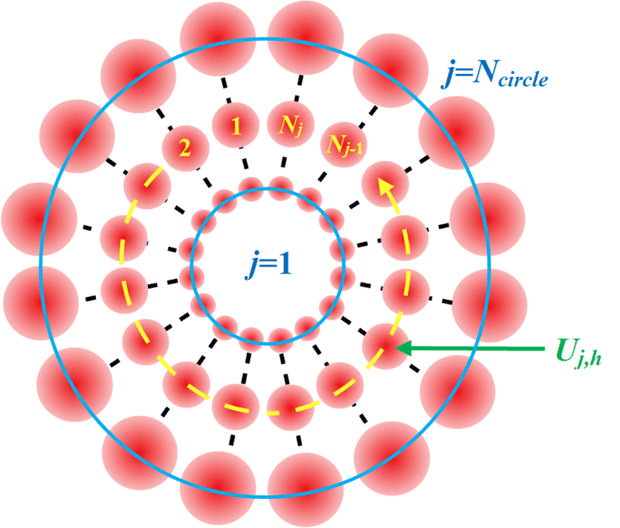
Now we give some numerical results to show the propagation properties and evolution of the optical field of the Gaussian beam array. First, the specific Gaussian beam array is set up using 12 Gaussian beams which are located on a circle. The intensity and phase distributions of the beam array in the near-field and far-field with different topological charges (from 1 to 4) are shown in Figure 3. Here it should be pointed out that the sizes of the observation screens in the near-field and far-field are respectively 0.2 m and 1 m.

Figure 3. Intensity distributions and phase patterns of the optical near-field and far-field with different topological charges from 1 to 4.
As depicted in Figure 3, we can see that the intensity distributions and phase patterns of all the optical far-fields have hollow forms in the center and vortex styles, respectively. With increasing topological charge, the radius of the hollow ring in the far-field increases and the corresponding energy fraction decreases. Moreover, we can see that the ever-present petals have an increasing energy fraction and a tendency of centralization when the resolution of the applied stair-like vortex phase, which is defined as the beam number that constitutes one
![]() $2\unicode[STIX]{x1D70B}$
piston phase difference, decreases. In particular, when the resolution of the applied phase is 3, which means the topological charge is 4, the central intensity distribution is no longer a regular ring, and deviates severely from an ordinary vortex beam. Therefore, in order to preserve the hollow ring intensity pattern, the resolution should be no less than 4. By rational design and suitable parameter selection, we can use a beam array to accurately approximate an arbitrary Laguerre–Gaussian (LG) beam, which is an orthogonal and complete mode in the spatial domain.
$2\unicode[STIX]{x1D70B}$
piston phase difference, decreases. In particular, when the resolution of the applied phase is 3, which means the topological charge is 4, the central intensity distribution is no longer a regular ring, and deviates severely from an ordinary vortex beam. Therefore, in order to preserve the hollow ring intensity pattern, the resolution should be no less than 4. By rational design and suitable parameter selection, we can use a beam array to accurately approximate an arbitrary Laguerre–Gaussian (LG) beam, which is an orthogonal and complete mode in the spatial domain.
2.3 Analysis of the orthogonality of the separated modes
One of the most important applications of OAM beams is improving the data capacity in communication systems, which is based on the principle that coaxially propagating OAM beams with different vortex phase states are orthogonal to each other and can be efficiently demodulated. The LG beams, which are complete orthogonal modes, fulfill the above conditions well and have been verified in light communication systems[Reference Willner, Huang, Yan, Ren, Ahmed, Xie, Bao, Li, Cao, Zhao, Wang, Lavery, Tur, Ramachandran, Molisch, Ashrafi and Ashrafi2]. Similarly, whether the vortex beam generated from array beams can be used to expand the data channel capacity depends on the orthogonality of the constructed beams.
Using Equation (3), we take two different constructed phase states with different integral topological charges
![]() $\ell _{1}$
and
$\ell _{1}$
and
![]() $\ell _{2}$
as examples to analyze whether they are orthogonal. The two optical fields can be expressed as follows:
$\ell _{2}$
as examples to analyze whether they are orthogonal. The two optical fields can be expressed as follows:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \overrightarrow{U}_{\!\!\text{array}\_B}(\overrightarrow{r},z=0)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{j=1}^{N_{\text{circle}}}\mathop{\sum }_{h=1}^{N_{j}}W_{j}(\overrightarrow{\unicode[STIX]{x1D70C}}_{\!\!j,h})A_{j}(\overrightarrow{\unicode[STIX]{x1D70C}}_{\!\!j,h})e^{i\frac{2\unicode[STIX]{x1D70B}}{N_{j}}h\ell _{B}},\nonumber\\ \displaystyle & & \displaystyle \qquad (B=1,2).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \overrightarrow{U}_{\!\!\text{array}\_B}(\overrightarrow{r},z=0)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{j=1}^{N_{\text{circle}}}\mathop{\sum }_{h=1}^{N_{j}}W_{j}(\overrightarrow{\unicode[STIX]{x1D70C}}_{\!\!j,h})A_{j}(\overrightarrow{\unicode[STIX]{x1D70C}}_{\!\!j,h})e^{i\frac{2\unicode[STIX]{x1D70B}}{N_{j}}h\ell _{B}},\nonumber\\ \displaystyle & & \displaystyle \qquad (B=1,2).\end{eqnarray}$$
For the case
![]() $\ell _{1}=\ell _{2}$
, we can derive that
$\ell _{1}=\ell _{2}$
, we can derive that
whereas for the case
![]() $\ell _{1}\neq \ell _{2}$
, after tedious but straightforward calculations, we can obtain that
$\ell _{1}\neq \ell _{2}$
, after tedious but straightforward calculations, we can obtain that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int \overrightarrow{U}_{\!\!\text{array}\_1}\overrightarrow{U}_{\!\text{array}\_2}^{\!\ast }\,\text{d}\unicode[STIX]{x1D703}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{j=1}^{N_{\text{circle}}}|W_{j}(\overrightarrow{\unicode[STIX]{x1D70C}}_{\!\!j})A_{1j}(\overrightarrow{\unicode[STIX]{x1D70C}}_{\!\!j})|^{2}\mathop{\sum }_{h=1}^{N_{j}}e^{i\frac{2\unicode[STIX]{x1D70B}}{N_{j}}h(\ell _{1}-\ell _{2})}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int \overrightarrow{U}_{\!\!\text{array}\_1}\overrightarrow{U}_{\!\text{array}\_2}^{\!\ast }\,\text{d}\unicode[STIX]{x1D703}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{j=1}^{N_{\text{circle}}}|W_{j}(\overrightarrow{\unicode[STIX]{x1D70C}}_{\!\!j})A_{1j}(\overrightarrow{\unicode[STIX]{x1D70C}}_{\!\!j})|^{2}\mathop{\sum }_{h=1}^{N_{j}}e^{i\frac{2\unicode[STIX]{x1D70B}}{N_{j}}h(\ell _{1}-\ell _{2})}.\end{eqnarray}$$
Using the relationship between complex exponentials and trigonometric functions and recalling the summation formula (see Chapter 1 Equation (1.342.2) in Ref. [Reference Gradshteyn and Ryzhik44]) expressed as
by switching to new variables of integration
![]() $\unicode[STIX]{x1D700}=h$
,
$\unicode[STIX]{x1D700}=h$
,
![]() $\unicode[STIX]{x1D6FA}=N_{j}$
, and
$\unicode[STIX]{x1D6FA}=N_{j}$
, and
![]() $x=2\unicode[STIX]{x1D70B}(\ell _{1}-\ell _{2})/N_{j}$
, Equation (7) is equal to
$x=2\unicode[STIX]{x1D70B}(\ell _{1}-\ell _{2})/N_{j}$
, Equation (7) is equal to
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{h=0}^{N_{j}}\cos \left[\frac{2\unicode[STIX]{x1D70B}}{N_{j}}(\ell _{1}-\ell _{2})h\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}\left\{1+\frac{\sin \left[\left(N_{j}+\frac{1}{2}\right)\frac{2\unicode[STIX]{x1D70B}}{N_{j}}(\ell _{1}-\ell _{2})\right]}{\sin \left[\frac{1}{2}\frac{2\unicode[STIX]{x1D70B}}{N_{j}}(\ell _{1}-\ell _{2})\right]}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{h=0}^{N_{j}}\cos \left[\frac{2\unicode[STIX]{x1D70B}}{N_{j}}(\ell _{1}-\ell _{2})h\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}\left\{1+\frac{\sin \left[\left(N_{j}+\frac{1}{2}\right)\frac{2\unicode[STIX]{x1D70B}}{N_{j}}(\ell _{1}-\ell _{2})\right]}{\sin \left[\frac{1}{2}\frac{2\unicode[STIX]{x1D70B}}{N_{j}}(\ell _{1}-\ell _{2})\right]}\right\}.\end{eqnarray}$$
Upon substituting Equations (7) and (8) into Equation (6), we can derive that
From Equations (5) and (9), we can see that the vortex beams constructed by array beams with different phase modulations are orthogonal and can be separated from each other, and thus can be exploited and applied in a wide variety of applications such as optical communication systems.
3 Experimental implementation
3.1 Experimental setup
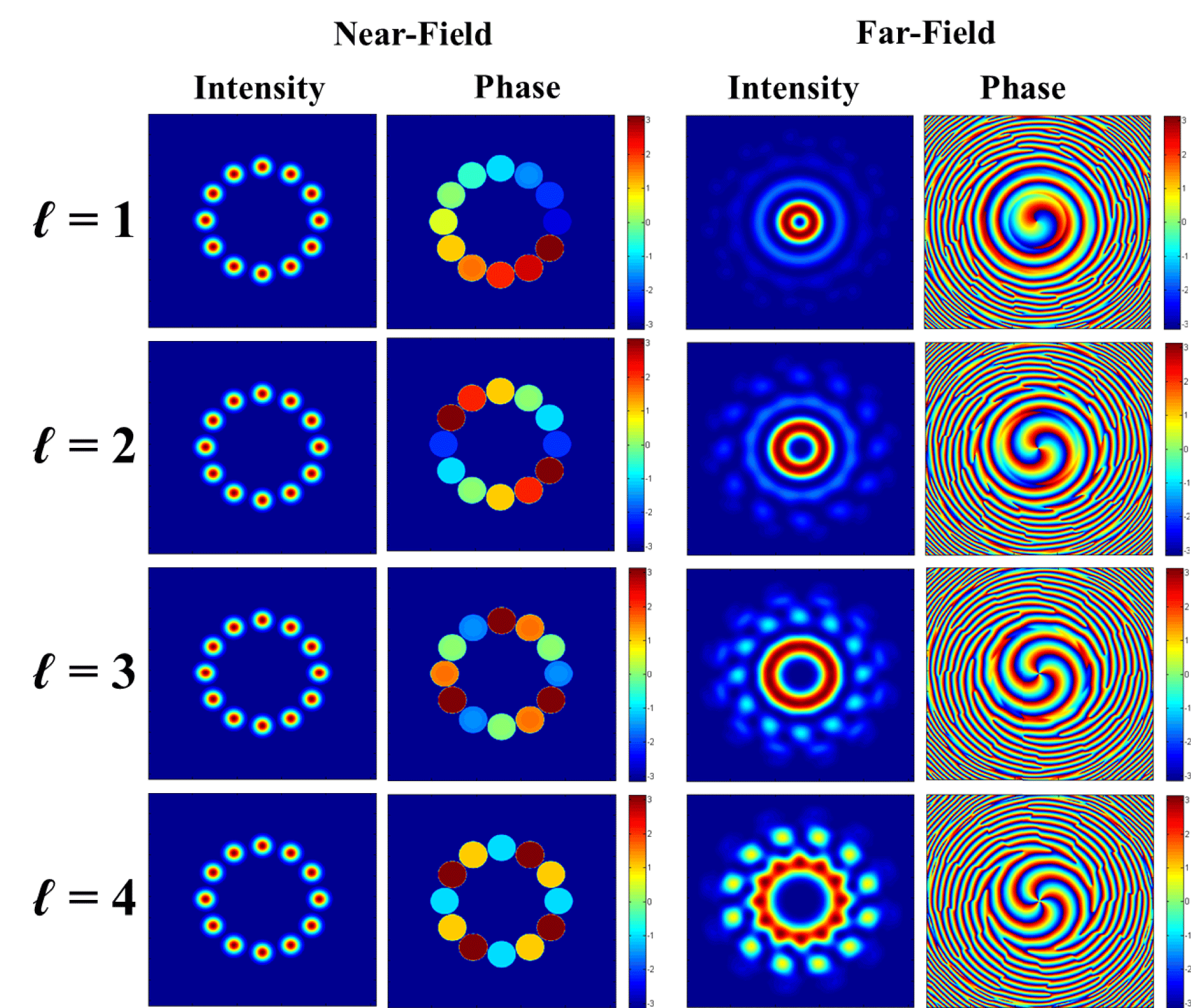
To verify the above theoretical analysis, an experimental platform based on CBC of fiber amplifiers (FAs), as shown in Figure 4, which can convert array beams into a vortex beam, is set up based on a six-element hexagonal fiber collimator array. As shown in Figure 4, the seed laser for the fiber amplifiers is a linearly polarized, single-frequency Yb-doped fiber seed laser (SL) with a wavelength of 1064 nm and a power of 40 mW. The seed laser is amplified by a pre-amplifier (PA) and the output power is boosted to 400 mW. Following that, a
![]() $1\times 8$
fiber splitter (FS) is used to split the pre-amplified laser into eight sub-beams, from which we choose six sub-beams to carry out the following experiment. Before sending them to the fiber amplifiers, each of the six selected fiber lasers is connected to a LiNbO3-based fiber phase modulator (FPM). The gain fiber of the fiber amplifier is double-clad fiber with a core/inner cladding diameter of
$1\times 8$
fiber splitter (FS) is used to split the pre-amplified laser into eight sub-beams, from which we choose six sub-beams to carry out the following experiment. Before sending them to the fiber amplifiers, each of the six selected fiber lasers is connected to a LiNbO3-based fiber phase modulator (FPM). The gain fiber of the fiber amplifier is double-clad fiber with a core/inner cladding diameter of
![]() $10~\unicode[STIX]{x03BC}\text{m}/125~\unicode[STIX]{x03BC}\text{m}$
, based on which the power of each channel is amplified to 1 W. Then a mode field adaptor (MFA, the input fiber is double-clad fiber with core/inner cladding diameter of
$10~\unicode[STIX]{x03BC}\text{m}/125~\unicode[STIX]{x03BC}\text{m}$
, based on which the power of each channel is amplified to 1 W. Then a mode field adaptor (MFA, the input fiber is double-clad fiber with core/inner cladding diameter of
![]() $10~\unicode[STIX]{x03BC}\text{m}/125~\unicode[STIX]{x03BC}\text{m}$
, and output fiber is double-clad fiber with core/inner cladding diameter of
$10~\unicode[STIX]{x03BC}\text{m}/125~\unicode[STIX]{x03BC}\text{m}$
, and output fiber is double-clad fiber with core/inner cladding diameter of
![]() $20~\unicode[STIX]{x03BC}\text{m}/400~\unicode[STIX]{x03BC}\text{m}$
) is used in each channel to connect the FPM to a fiber end-cap, which is spliced with a
$20~\unicode[STIX]{x03BC}\text{m}/400~\unicode[STIX]{x03BC}\text{m}$
) is used in each channel to connect the FPM to a fiber end-cap, which is spliced with a
![]() $20~\unicode[STIX]{x03BC}\text{m}/400~\unicode[STIX]{x03BC}\text{m}$
delivery fiber and acts as the output terminal of the fiber laser. Next, the array beams emitted from the end-caps are collimated by an in-house-made collimator array with a focal length of 800 mm and a clear aperture (
$20~\unicode[STIX]{x03BC}\text{m}/400~\unicode[STIX]{x03BC}\text{m}$
delivery fiber and acts as the output terminal of the fiber laser. Next, the array beams emitted from the end-caps are collimated by an in-house-made collimator array with a focal length of 800 mm and a clear aperture (
![]() $d$
) of 58 mm, which generates a collimated Gaussian beam array with a beam waist width
$d$
) of 58 mm, which generates a collimated Gaussian beam array with a beam waist width
![]() $\unicode[STIX]{x1D714}_{0}$
of 32.5 mm and a beam truncation factor (
$\unicode[STIX]{x1D714}_{0}$
of 32.5 mm and a beam truncation factor (
![]() $2\unicode[STIX]{x1D714}_{0}/d$
) of 1.12[Reference Zhi, Zhang, Ma, Wang, Chen, Wu, Zhou and Si45].
$2\unicode[STIX]{x1D714}_{0}/d$
) of 1.12[Reference Zhi, Zhang, Ma, Wang, Chen, Wu, Zhou and Si45].
The collimated beam array then is separated into two parts:
![]() $\unicode[STIX]{x2460}$
a high-power beam array with OAM and
$\unicode[STIX]{x2460}$
a high-power beam array with OAM and
![]() $\unicode[STIX]{x2461}$
a low-power sampling beam array on passing through a high-reflectivity mirror (HRM1 in Figure 4). Beam array
$\unicode[STIX]{x2461}$
a low-power sampling beam array on passing through a high-reflectivity mirror (HRM1 in Figure 4). Beam array
![]() $\unicode[STIX]{x2460}$
is the principal generated high-power vortex beam that is to be utilized in applications (for example, long distance optical communication). Beam array
$\unicode[STIX]{x2460}$
is the principal generated high-power vortex beam that is to be utilized in applications (for example, long distance optical communication). Beam array
![]() $\unicode[STIX]{x2461}$
is used for the main phase-control, which just needs to sample a small power fraction to generate a stable vortex-like stair phase array. Next, the sampling beam array
$\unicode[STIX]{x2461}$
is used for the main phase-control, which just needs to sample a small power fraction to generate a stable vortex-like stair phase array. Next, the sampling beam array
![]() $\unicode[STIX]{x2461}$
is projected into a modified Newtonian reflector telescope beam shrinking system to reduce its size to less than that of the spatial light modulator (SLM), which is used here to precisely generate the required piston phase array and is controlled by a desktop computer. As depicted in Figure 4, the compressed beam array
$\unicode[STIX]{x2461}$
is projected into a modified Newtonian reflector telescope beam shrinking system to reduce its size to less than that of the spatial light modulator (SLM), which is used here to precisely generate the required piston phase array and is controlled by a desktop computer. As depicted in Figure 4, the compressed beam array
![]() $\unicode[STIX]{x2462}$
is divided into two parts by means of a beam splitter prism (BSP). The reflected part
$\unicode[STIX]{x2462}$
is divided into two parts by means of a beam splitter prism (BSP). The reflected part
![]() $\unicode[STIX]{x2463}$
is modulated and reflected by the SLM, whereas the transmitted part
$\unicode[STIX]{x2463}$
is modulated and reflected by the SLM, whereas the transmitted part
![]() $\unicode[STIX]{x2464}$
without the applied piston phase array is focused directly by a focusing lens (FL1) with a focal length of 1 m and detected by a charge coupled device (CCD). If the impact of size is ignored, part
$\unicode[STIX]{x2464}$
without the applied piston phase array is focused directly by a focusing lens (FL1) with a focal length of 1 m and detected by a charge coupled device (CCD). If the impact of size is ignored, part
![]() $\unicode[STIX]{x2464}$
has the same phase and intensity distributions as part
$\unicode[STIX]{x2464}$
has the same phase and intensity distributions as part
![]() $\unicode[STIX]{x2460}$
. Part
$\unicode[STIX]{x2460}$
. Part
![]() $\unicode[STIX]{x2465}$
is then converted to a beam array with a spiral staircase phase array. After being reflected by HRM2 and focused by FL2 (focal length 2 m), the far-field of part
$\unicode[STIX]{x2465}$
is then converted to a beam array with a spiral staircase phase array. After being reflected by HRM2 and focused by FL2 (focal length 2 m), the far-field of part
![]() $\unicode[STIX]{x2465}$
is simultaneously detected by CCD2 and a photon detector (PD), in front of which a pinhole with a diameter of
$\unicode[STIX]{x2465}$
is simultaneously detected by CCD2 and a photon detector (PD), in front of which a pinhole with a diameter of
![]() $80~\unicode[STIX]{x03BC}\text{m}$
is attached.
$80~\unicode[STIX]{x03BC}\text{m}$
is attached.

Figure 4. Experimental setup of the high-power vortex beam generation system using the array beams CBC technique. (SL: seed laser; PA: pre-amplifier; FS: fiber splitter; FPM: fiber phase modulator; FA: fiber amplifier; MFA: mode field adaptor; HRM: high-reflectivity mirror; SLM: spatial light modulator; BSP: beam splitter prism;
![]() $\unicode[STIX]{x2460}$
: high-power beam array with OAM;
$\unicode[STIX]{x2460}$
: high-power beam array with OAM;
![]() $\unicode[STIX]{x2461}$
: low-power sampling beam array;
$\unicode[STIX]{x2461}$
: low-power sampling beam array;
![]() $\unicode[STIX]{x2462}$
: shrinking beam array;
$\unicode[STIX]{x2462}$
: shrinking beam array;
![]() $\unicode[STIX]{x2463}$
: beam array incident on SLM;
$\unicode[STIX]{x2463}$
: beam array incident on SLM;
![]() $\unicode[STIX]{x2464}$
: beam array without SLM phase modulation;
$\unicode[STIX]{x2464}$
: beam array without SLM phase modulation;
![]() $\unicode[STIX]{x2465}$
: beam array with SLM phase modulation; FL: focus lens; PD: photon detector; CCD: charge coupled device; FPGA: field programmable gate array.)
$\unicode[STIX]{x2465}$
: beam array with SLM phase modulation; FL: focus lens; PD: photon detector; CCD: charge coupled device; FPGA: field programmable gate array.)
The intensity distributions of the two beams
![]() $\unicode[STIX]{x2464}$
and
$\unicode[STIX]{x2464}$
and
![]() $\unicode[STIX]{x2465}$
, which represent the situations before and after piston phase array addition and are detected by CCD1 and CCD2, respectively, are monitored by a laptop computer in real time. A PD with a 150 MHz bandwidth is used to provide feedback data for phase-locking control. The signal collected by the PD is observed using an oscilloscope and processed by a field programmable gate array (FPGA) controller. The output control signals produced from the FPGA controller are applied on the FPMs to control the array beams to an equiphase status. During the experiment, a single-frequency dithering algorithm is used in the FPGA controller to perform the phase-locking control.
$\unicode[STIX]{x2465}$
, which represent the situations before and after piston phase array addition and are detected by CCD1 and CCD2, respectively, are monitored by a laptop computer in real time. A PD with a 150 MHz bandwidth is used to provide feedback data for phase-locking control. The signal collected by the PD is observed using an oscilloscope and processed by a field programmable gate array (FPGA) controller. The output control signals produced from the FPGA controller are applied on the FPMs to control the array beams to an equiphase status. During the experiment, a single-frequency dithering algorithm is used in the FPGA controller to perform the phase-locking control.
3.2 Important points regarding the setup
For the above-mentioned experimental setup, the importance of the beam shrinking system needs to be explained.
As we know, the far-field diffraction angle of a collimated beam can be calculated using
![]() $\unicode[STIX]{x1D703}\propto \unicode[STIX]{x1D706}/D$
, where
$\unicode[STIX]{x1D703}\propto \unicode[STIX]{x1D706}/D$
, where
![]() $\unicode[STIX]{x1D706}$
is the wavelength and
$\unicode[STIX]{x1D706}$
is the wavelength and
![]() $D$
is the diameter of the collimated beam. Without the beam shrinking system, the size of the array beams must be very small in order to fit within the size of the liquid crystal screen in the SLM. As the liquid crystal screen is just a dozen millimeters, the size of the incident array beams will be limited to the millimeter level. Thus the diffraction angle of a single beam will be about the milliradian level. This means that when the receiver aperture is 1 m, the propagation distance should be less than 1 km. Therefore these small array beams cannot be utilized in applications that require long propagation distances. In our system, the size of the collimated beam has been expanded by the Newtonian telescope by a factor of more than 30 with respect to that incident on the SLM. In an experiment using OAM superposition modes of light transmitted through a 3 km intra-city channel in Vienna that was described in Ref. [Reference Krenn, Fickler, Fink, Handsteiner, Malik, Scheidl, Ursin and Zeilinger20], a telescope was also used to expand the OAM beam to a diameter of approximately 60 mm, which was then projected as a larger beam to free-space for propagation and reception. By careful calculations, the effective operating distance of our designed system reaches more than 60 km with a 1 m receiver. Thus this system has great potential for applications in optical communication systems along both ground-to-space or space-to-ground paths.
$D$
is the diameter of the collimated beam. Without the beam shrinking system, the size of the array beams must be very small in order to fit within the size of the liquid crystal screen in the SLM. As the liquid crystal screen is just a dozen millimeters, the size of the incident array beams will be limited to the millimeter level. Thus the diffraction angle of a single beam will be about the milliradian level. This means that when the receiver aperture is 1 m, the propagation distance should be less than 1 km. Therefore these small array beams cannot be utilized in applications that require long propagation distances. In our system, the size of the collimated beam has been expanded by the Newtonian telescope by a factor of more than 30 with respect to that incident on the SLM. In an experiment using OAM superposition modes of light transmitted through a 3 km intra-city channel in Vienna that was described in Ref. [Reference Krenn, Fickler, Fink, Handsteiner, Malik, Scheidl, Ursin and Zeilinger20], a telescope was also used to expand the OAM beam to a diameter of approximately 60 mm, which was then projected as a larger beam to free-space for propagation and reception. By careful calculations, the effective operating distance of our designed system reaches more than 60 km with a 1 m receiver. Thus this system has great potential for applications in optical communication systems along both ground-to-space or space-to-ground paths.
4 Experimental results and analysis
4.1 Vortex beam generation
First, we experimentally test the feasibility of the real-time phase-locking (PL) control system based on a single-frequency dithering technique[Reference Ma, Zhou, Wang, Ma, Xu, Si, Liu and Zhao46]. Figure 5(a) shows the normalized voltage values detected by the PD in different situations to investigate incoherent and coherent combining effects. We can see that without PL control, the voltage detected by the PD fluctuates randomly with time with a normalized value of 0.346 averaged over 25 s. When the active PL control is on, the average value of the normalized voltage increases sharply to above 0.95 in about 6.2 ms. By careful data analysis, we calculate the normalized mean voltage value as about 0.963 over 25 s with a root mean square (RMS) value
![]() $V_{\text{rms}}$
of 0.010. We also calculate the spectral density of the phase noise power with and without PL by Fourier transforming the voltage signal in the time domain, as shown in Figure 5(b). It is clear by comparing the two curves that phase noise frequencies below 100 Hz have been efficiently suppressed when the PL control is on.
$V_{\text{rms}}$
of 0.010. We also calculate the spectral density of the phase noise power with and without PL by Fourier transforming the voltage signal in the time domain, as shown in Figure 5(b). It is clear by comparing the two curves that phase noise frequencies below 100 Hz have been efficiently suppressed when the PL control is on.

Figure 5. Normalized voltage values detected by the PD and corresponding spectral densities of the phase noise power. (a) Time-dependent normalized voltages. (b) Corresponding spectral densities.

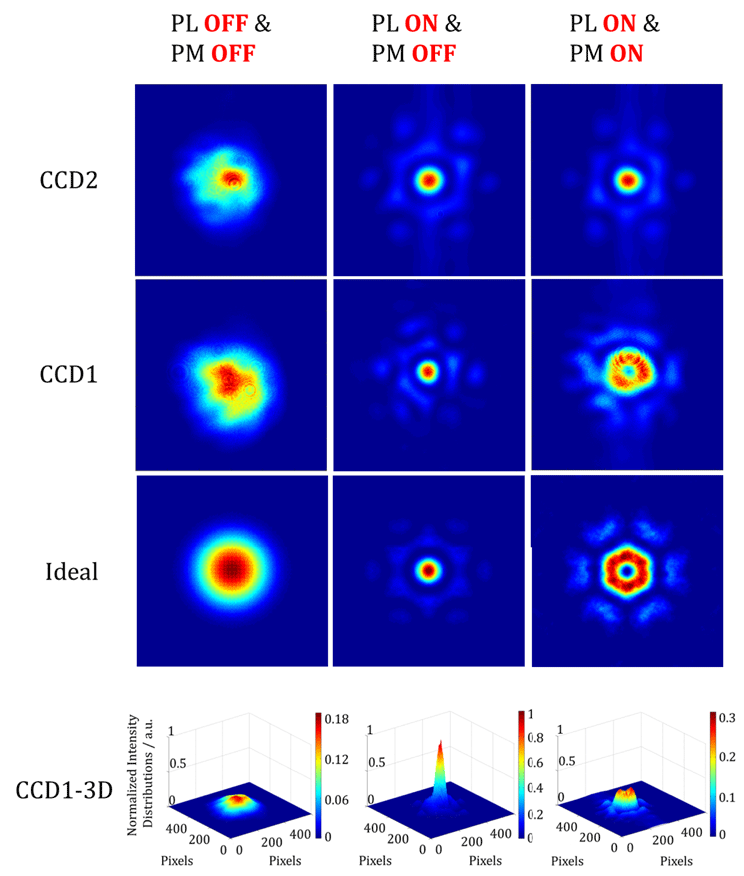
Figure 6. Long-exposure beam patterns in different situations (see Visualization for dynamic experimental recording).
With this strong foundation of PL control, which is most important in the CBC technique, we next carry out the vortex beam generation experiment by applying phase modulation (PM) using the SLM. The performances of PL and PM can both be directly tested and observed using the long-exposure beam pattern from the cameras CCD1 and CCD2. Figure 6 shows the intensity distributions in different situations. The beam patterns in the first row represent an exposure of 20 s detected by CCD2. As a monitor of PL, the patterns in CCD2 can only distinguish the incoherent and coherent states. That is to say, when PL is on, the beam array is in a steady coherent state no matter whether PM is on or off. As shown in the figure, the second and fourth rows respectively represent the two-dimensional and three-dimensional long-exposure intensity distributions acquired by CCD1. The beam array detected by CCD1 truly represents the high-power beam array
![]() $\unicode[STIX]{x2460}$
shown in Figure 4. When PL and PM are both off, the phase differences between the array beams are time-varying and the long-exposure beam pattern is close to a Gaussian beam, which is similar to the ideal incoherent combining situation shown in the first picture in the third row. When only the active PL is on, the array beams are efficiently controlled to be highly coherent with each other. The coherent pattern shows a significant increase in the intensity of the central lobe along with a high fringe contrast up to 95.4%. From calculations, the normalized maximum value of the beam intensity distribution increases from 0.19 to 1, which means the beam brightness of the CBC state increases by almost 5.6 times compared with the incoherent situation. From this point of view, the CBC experiment has reached
$\unicode[STIX]{x2460}$
shown in Figure 4. When PL and PM are both off, the phase differences between the array beams are time-varying and the long-exposure beam pattern is close to a Gaussian beam, which is similar to the ideal incoherent combining situation shown in the first picture in the third row. When only the active PL is on, the array beams are efficiently controlled to be highly coherent with each other. The coherent pattern shows a significant increase in the intensity of the central lobe along with a high fringe contrast up to 95.4%. From calculations, the normalized maximum value of the beam intensity distribution increases from 0.19 to 1, which means the beam brightness of the CBC state increases by almost 5.6 times compared with the incoherent situation. From this point of view, the CBC experiment has reached
![]() $5.6/6=93.3\%$
of the ideal calculation result. Furthermore, when the PM is applied together with the PL, the wavefront of the beam array is superposed with a spiral-stair-like phase array on the basis of perfect coherence, and a beam array carrying OAM is generated. As shown in the figure, the beam pattern has a non-circular hollow shape in the center, with six petals around the central part. By careful data processing, the fringe contrast of the central hollow beam is found to be about 73.5%. By observation and analysis, we can see that the far-field distributions of the OAM beam obtained in the experiment basically match the ideal situation except for some small differences between the two shapes. The differences come mainly from the high-order mode induced by the MFA in each channel and residual phase errors from the PL control system. As the phase differences of the array beams are precisely controlled in a state that satisfies the required piston phase array, this hollow shape is stable in the time domain.
$5.6/6=93.3\%$
of the ideal calculation result. Furthermore, when the PM is applied together with the PL, the wavefront of the beam array is superposed with a spiral-stair-like phase array on the basis of perfect coherence, and a beam array carrying OAM is generated. As shown in the figure, the beam pattern has a non-circular hollow shape in the center, with six petals around the central part. By careful data processing, the fringe contrast of the central hollow beam is found to be about 73.5%. By observation and analysis, we can see that the far-field distributions of the OAM beam obtained in the experiment basically match the ideal situation except for some small differences between the two shapes. The differences come mainly from the high-order mode induced by the MFA in each channel and residual phase errors from the PL control system. As the phase differences of the array beams are precisely controlled in a state that satisfies the required piston phase array, this hollow shape is stable in the time domain.
4.2 Spiral phase verification
To verify that the phase of the OAM beam obtained in the above experiment has a spiral distribution, we need to carry out another interference experiment to examine the OAM state. In general, the interference fringes for OAM verification have two types. One is the ‘Y’-shape interferogram generated from the interference of the OAM beam and a plane wave beam. From the direction and number of furcations in the interferogram we can infer how many OAMs the beam carries. The other type is the helical structure, which comes from the interference between the vortex beam and a spherical wave. From observation of the direction and number of furcations in this method, we can tell the OAM number of the measured beam.
For testing our generated vortex beam, the difficulty is in finding a coherent laser beam with a stable phase structure (plane or spherical). As the vortex beam is generated from an array of beams, an arbitrary single beam with a plane or spherical wavefront is not suitable for the interference experiment. As we know, beam
![]() $\unicode[STIX]{x2465}$
is an approximately plane wave constructed by the same beam array under the CBC. Thus, to measure the OAM state in the vortex beam obtained in the previous section, we set up another experiment based on the original parameters. As depicted in Figure 7(a), we separate a part of beam
$\unicode[STIX]{x2465}$
is an approximately plane wave constructed by the same beam array under the CBC. Thus, to measure the OAM state in the vortex beam obtained in the previous section, we set up another experiment based on the original parameters. As depicted in Figure 7(a), we separate a part of beam
![]() $\unicode[STIX]{x2465}$
using a beam splitter mirror (BSM) and HRM3. Then beams
$\unicode[STIX]{x2465}$
using a beam splitter mirror (BSM) and HRM3. Then beams
![]() $\unicode[STIX]{x2464}$
and
$\unicode[STIX]{x2464}$
and
![]() $\unicode[STIX]{x2465}$
are focused by FL1 together and the interference pattern at the focus point of FL1 is observed by CCD1.
$\unicode[STIX]{x2465}$
are focused by FL1 together and the interference pattern at the focus point of FL1 is observed by CCD1.
When the OAM number
![]() $\ell =+1$
, the beam array is applied as a counterclockwise phase array, as shown in the red curve in Figure 7(b). The corresponding theoretical and experimental interference patterns are depicted as Figures 7(c) and 7(d), respectively. The special interferogram has a forked fringe with an inverted ‘Y’ shape in the center, which indicates the number of the OAM carried by the beam array is
$\ell =+1$
, the beam array is applied as a counterclockwise phase array, as shown in the red curve in Figure 7(b). The corresponding theoretical and experimental interference patterns are depicted as Figures 7(c) and 7(d), respectively. The special interferogram has a forked fringe with an inverted ‘Y’ shape in the center, which indicates the number of the OAM carried by the beam array is
![]() $+1$
. The position of bifurcation is at the location of a phase singularity. When we apply a clockwise phase array on the beam array, as shown in Figure 7(e), the central part of the interferogram switches to an erect ‘Y’ shape fringe (Figures 7(f) and 7(g)). Through the test experiment, we find that the generated vortex beam carries the OAM we predicted, and the topological charge is consistent with that imposed by the SLM.
$+1$
. The position of bifurcation is at the location of a phase singularity. When we apply a clockwise phase array on the beam array, as shown in Figure 7(e), the central part of the interferogram switches to an erect ‘Y’ shape fringe (Figures 7(f) and 7(g)). Through the test experiment, we find that the generated vortex beam carries the OAM we predicted, and the topological charge is consistent with that imposed by the SLM.

Figure 7. (a) Experimental setup and (b)–(g) interference results of the OAM measurement. (b) Intensity and phase distributions of beams
![]() $\unicode[STIX]{x2464}$
and
$\unicode[STIX]{x2464}$
and
![]() $\unicode[STIX]{x2465}$
with the number of the OAM set to
$\unicode[STIX]{x2465}$
with the number of the OAM set to
![]() $\ell =+1$
; (c), (d) corresponding interference patterns of the theoretical and experimental results. (e), (g) Results for the case
$\ell =+1$
; (c), (d) corresponding interference patterns of the theoretical and experimental results. (e), (g) Results for the case
![]() $\ell =-1$
.
$\ell =-1$
.
5 Discussion and conclusions
In this paper, we have first proposed a generating method for a high-power vortex beam using the array beams coherent combination technique. By theoretical analysis, we investigated the characteristics of this method and the orthogonality of the generated OAM beams with different modes. Then we experimentally implemented a high-power beam carrying OAM by CBC of a fiber amplifier array. Based on CBC and the optimum piston phase applied by the SLM, we finally obtained novel vortex beams carrying OAM of
![]() $\pm 1$
, both basically coinciding with the ideal situations.
$\pm 1$
, both basically coinciding with the ideal situations.
The differences in performance between the experimentally obtained vortex beam and the theoretical results arise mainly from the not strictly fundamental mode operation of the beamlets, tilt aberrations caused by environmental conditions, and residual phase errors in the piston phase-control system. The limits of our approach include the performance of the single-channel fiber laser (including power, line width, polarization, beam quality), the number of combined beams, the precision of the control system and the spatial resolution of the SLM. In terms of the phase modulation methods, beyond the use of the SLM, we also may use specially designed amplitude/phase masks for the generation of some specific novel beams.
As the array-beams-generated OAM beams with different eigenstates are orthogonal to each other, they can be used to increase the signal channel capacity in optical communication systems. The high-power OAM beam can be used in many applications besides free space communications, such as high-resolution imaging and special material processing[Reference Li, Yao, Yu, Xia and Zhou47]. In particular, for the destruction of necrotic biological tissue in the field of biomedical treatment, high-power vortex beams (like the ring Airy–Gaussian beam) have great potential and advantages[Reference Chen, Chen, Peng, Peng, Zhou and Deng48]. Additionally, the manipulation of micro-particles under the radiation of high-power OAM beams may show improved performance.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (NSFC) (Nos. 61405255, 61378034, and 11504424) and the Graduate Student Innovation Foundation through the National University of Defense Technology, China (No. B150705). The authors thank Ph.D candidates Lei Li and Kun Xie, Dr. Wuming Wu, Dr. Zilun Chen and Dr. Yu Ning for their help with the experiment.