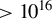1 Introduction
In inertial confinement fusion (ICF) experiments, laser plasma instabilities (LPIs) such as stimulated Raman scattering (SRS), stimulated Brillouin scattering (SBS) and two-plasmon decay (TPD) instability are never avoided, even if several approaches, including direct-drive[ Reference Bodner, Colombant, Gardner, Lehmberg, Obenschain, Phillips, Schmitt, Sethian, McCrory, Seka, Verdon, Knauer, Afeyan and Powell 1 – Reference Weber and Riconda 4 ], indirect-drive[ Reference Lindl 5 – Reference Lindl, Amendt, Berger, Glendinning, Glenzer, Haan, Kauffman, Landen and Suter 7 ] and hybrid-drive[ Reference He, Li, Fan, Wang, Liu, Lan, Wu and Ye 8 ], have been proposed to achieve ICF. Generally, LPIs are expected to be suppressed in ICF experiments because they do harm to ICF[ Reference Bodner, Colombant, Gardner, Lehmberg, Obenschain, Phillips, Schmitt, Sethian, McCrory, Seka, Verdon, Knauer, Afeyan and Powell 1 , Reference Lindl 5 ]. Backward SRS (BSRS) and SBS take away part of the laser energy and weaken the drive intensity, side SRS (SSRS) and side SBS change the laser propagation direction, which results in uncontrollable drive symmetry, and SRS and TPD generate super-hot electrons that may decrease the implosion efficiency.
Significant progresses in LPI studies have been achieved during recent decades[
Reference Montgomery
9
–
Reference Cristoforetti, Antonelli, Mancelli, Atzeni, Baffigi, Barbato, Batani, Boutoux, Amato, Dostal, Dudzak, Filippov, Gu, Juha, Klimo, Krus, Malko, Martynenko, Nicolai, Ospina, Pikuz, Renner, Santos, Tikhonchuk, Trela, Viciani, Volpe, Weber and Gizzi
11
], but there are still many LPI problems remaining unclarified. Among them, nonlinearities[
Reference Russell, DuBois and Rose
12
] are the most important and highlighted, since nonlinear processes govern the saturation of LPIs (which decide the final energy loss from LPIs) in ICF experiments. Nonlinearities are usually involved in the behaviors of daughter waves, including the scattered lights or the electrostatic waves. The most common nonlinearities involved in electrostatic waves are high-order harmonics generation (HHG)[
Reference Xiao, Liu, Huang, Zheng, Qiao and He
13
,
Reference Liu and Dodin
14
], particle trapping[
Reference Kruer, Dawson and Sudan
15
,
Reference Vu, DuBois and Bezzerides
16
], daughter wave decay[
Reference Kolber, Rozmus and Tikhonchuk
17
–
Reference Zhao, Sheng, Weng, Ji and Zhu
20
], wave collapse[
Reference Russell, DuBois and Rose
12
], etc. The parameter
![]() $k{\lambda}_{\mathrm{d}}$
, where
$k{\lambda}_{\mathrm{d}}$
, where
![]() $k$
is the wave number of electrostatic wave and
$k$
is the wave number of electrostatic wave and
![]() ${\lambda}_{\mathrm{d}}$
is the Debye length of the plasma, will decide which nonlinearity is the dominated one. For electron-plasma waves (EPWs), kinetic nonlinearities such as electron trapping[
Reference Kruer, Dawson and Sudan
15
,
Reference Vu, DuBois and Bezzerides
16
] are dominated when
${\lambda}_{\mathrm{d}}$
is the Debye length of the plasma, will decide which nonlinearity is the dominated one. For electron-plasma waves (EPWs), kinetic nonlinearities such as electron trapping[
Reference Kruer, Dawson and Sudan
15
,
Reference Vu, DuBois and Bezzerides
16
] are dominated when
![]() ${k}_{\mathrm{epw}}{\lambda}_{\mathrm{d}}>0.3$
; otherwise, fluid nonlinearities such as LDI[
Reference Kolber, Rozmus and Tikhonchuk
17
–
Reference Depierreux, Labaune, Fuchs, Pesme, Tikhonchuk and Baldis
19
] are dominated. Since the parameter
${k}_{\mathrm{epw}}{\lambda}_{\mathrm{d}}>0.3$
; otherwise, fluid nonlinearities such as LDI[
Reference Kolber, Rozmus and Tikhonchuk
17
–
Reference Depierreux, Labaune, Fuchs, Pesme, Tikhonchuk and Baldis
19
] are dominated. Since the parameter
![]() ${k}_{\mathrm{epw}}{\lambda}_{\mathrm{d}}$
is quite sensitive to the plasma conditions (temperature and density) because
${k}_{\mathrm{epw}}{\lambda}_{\mathrm{d}}$
is quite sensitive to the plasma conditions (temperature and density) because
![]() ${\lambda}_{\mathrm{d}}={v}_{\mathrm{te}}/{\omega}_{\mathrm{pe}}$
, where
${\lambda}_{\mathrm{d}}={v}_{\mathrm{te}}/{\omega}_{\mathrm{pe}}$
, where
![]() ${v}_{\mathrm{te}}$
is the thermal velocity of the electron plasma,
${v}_{\mathrm{te}}$
is the thermal velocity of the electron plasma,
![]() ${\omega}_{\mathrm{pe}}=\sqrt{4\pi {n}_{\mathrm{e}}{e}^2/{m}_{\mathrm{e}}}$
is the electron-plasma frequency,
${\omega}_{\mathrm{pe}}=\sqrt{4\pi {n}_{\mathrm{e}}{e}^2/{m}_{\mathrm{e}}}$
is the electron-plasma frequency,
![]() ${n}_{\mathrm{e}}$
is the electron density,
${n}_{\mathrm{e}}$
is the electron density,
![]() ${m}_{\mathrm{e}}$
is the electron mass and
${m}_{\mathrm{e}}$
is the electron mass and
![]() $e$
is the electron charge.
$e$
is the electron charge.
![]() ${k}_{\mathrm{epw}}$
is sensitive to plasma conditions, and nonlinearities involved in EPWs are quite complex in ICF experiments where the plasma conditions are totally uncontrollable. As for nonlinearities involved in scattered lights, when their intensities reach certain thresholds, they may also decay into two new daughter waves, which may cause saturation of LPIs. For example, scattered lights of SRS may be re-scattered or excite TPD, as was reported in our previous work. Besides saturation, nonlinearities govern another important process, which is hot or super-hot-electron (or ion) generation. However, many nonlinear processes are still unclear in ICF experiments. In indirect-drive ICF conditions, electrons generated by SRS are usually below 100 keV, but both re-scattering[
Reference Winjum, Fahlen, Tsung and Mori
21
] and TPD of the scattered light of SRS[
Reference Pan, Jiang, Wang, Guo, Li, Li, Yang, Zheng, Zhang and He
22
] may generate super-hot electrons with energy that exceeds 100 keV, which were detected in ICF experiments[
Reference Dewald, Thomas, Hunter, Divol, Meezan, Glenzer, Suter, Bond, Kline, Celeste, Bradley, Bell, Kauffman, Kilkenny and Landen
23
]. However, these secondary processes caused by nonlinearities are usually ignored or attract less attention because they are difficult to detect in experiments. As a result, to give a better picture of hot-electron sources, secondary instabilities should be deeply studied theoretically or numerically.
${k}_{\mathrm{epw}}$
is sensitive to plasma conditions, and nonlinearities involved in EPWs are quite complex in ICF experiments where the plasma conditions are totally uncontrollable. As for nonlinearities involved in scattered lights, when their intensities reach certain thresholds, they may also decay into two new daughter waves, which may cause saturation of LPIs. For example, scattered lights of SRS may be re-scattered or excite TPD, as was reported in our previous work. Besides saturation, nonlinearities govern another important process, which is hot or super-hot-electron (or ion) generation. However, many nonlinear processes are still unclear in ICF experiments. In indirect-drive ICF conditions, electrons generated by SRS are usually below 100 keV, but both re-scattering[
Reference Winjum, Fahlen, Tsung and Mori
21
] and TPD of the scattered light of SRS[
Reference Pan, Jiang, Wang, Guo, Li, Li, Yang, Zheng, Zhang and He
22
] may generate super-hot electrons with energy that exceeds 100 keV, which were detected in ICF experiments[
Reference Dewald, Thomas, Hunter, Divol, Meezan, Glenzer, Suter, Bond, Kline, Celeste, Bradley, Bell, Kauffman, Kilkenny and Landen
23
]. However, these secondary processes caused by nonlinearities are usually ignored or attract less attention because they are difficult to detect in experiments. As a result, to give a better picture of hot-electron sources, secondary instabilities should be deeply studied theoretically or numerically.
In this paper, with the help of 2D particle-in-cell (PIC) simulations[
Reference Brady and Arber
24
], we discuss the competition among three instabilities, namely two secondary instabilities, which are the TPD of the backscattered light and filamentation of the EPWs, and a primary instability, which is the SSRS of the laser. As discussed in our previous work[
Reference Pan, Jiang, Wang, Guo, Li, Li, Yang, Zheng, Zhang and He
22
], the TPD of the backscattered light will be excited in a plasma with an electron density near
![]() $0.1{n}_{\mathrm{c}}$
(where
$0.1{n}_{\mathrm{c}}$
(where
![]() ${n}_{\mathrm{c}}\approx 1.17\times {10}^{21}$
cm
${n}_{\mathrm{c}}\approx 1.17\times {10}^{21}$
cm
![]() ${}^{-3}/{\lambda}_0^2$
is the critical density of the laser and
${}^{-3}/{\lambda}_0^2$
is the critical density of the laser and
![]() ${\lambda}_0$
is the laser wavelength in unit μm) and this secondary instability will suppress BSRS and generate super-hot electrons with energy exceeding 100 keV. Here it is further found that this secondary instability will compete with another two instabilities, one of which is filamentation of the EPWs and the other is SSRS of the laser. It is shown that when the laser intensity is relatively low, BSRS and TPD will coexist in early stage. In later stage, BSRS will be suppressed. When the laser is intense enough, the two instabilities also coexist in the early stage; however, the suppressed instability changes to TPD in the latter stage. The comparison of electron distribution functions implies that trapped-particle-modulation instability (TPMI)[
Reference Rose
25
–
Reference Berger, Brunner, Banks, Cohen and Winjum
28
] is responsible for filamentation of the EPWs, which is one reason for the suppression of TPD. This paper is arranged as follows: the first part is the introduction, the second part introduces the simulation setups in detail, the third part gives a discussion of the simulation results and the last part is the conclusion.
${\lambda}_0$
is the laser wavelength in unit μm) and this secondary instability will suppress BSRS and generate super-hot electrons with energy exceeding 100 keV. Here it is further found that this secondary instability will compete with another two instabilities, one of which is filamentation of the EPWs and the other is SSRS of the laser. It is shown that when the laser intensity is relatively low, BSRS and TPD will coexist in early stage. In later stage, BSRS will be suppressed. When the laser is intense enough, the two instabilities also coexist in the early stage; however, the suppressed instability changes to TPD in the latter stage. The comparison of electron distribution functions implies that trapped-particle-modulation instability (TPMI)[
Reference Rose
25
–
Reference Berger, Brunner, Banks, Cohen and Winjum
28
] is responsible for filamentation of the EPWs, which is one reason for the suppression of TPD. This paper is arranged as follows: the first part is the introduction, the second part introduces the simulation setups in detail, the third part gives a discussion of the simulation results and the last part is the conclusion.
2 Particle-in-cell simulation setups
Two simulations, named cases 1 and 2, are performed in this paper. Except for the laser intensity, all the simulation parameters are the same in both cases. The laser intensities in cases 1 and 2 are 4.45
![]() $\times {10}^{15}$
and 1
$\times {10}^{15}$
and 1
![]() $\times {10}^{16}$
W/cm2, respectively. Correspondingly, the normalized vector potentials (which are defined as
$\times {10}^{16}$
W/cm2, respectively. Correspondingly, the normalized vector potentials (which are defined as
![]() ${a}_0={eE}_{\mathrm{L}}/{m}_{\mathrm{e}}{\omega}_0c$
, where
${a}_0={eE}_{\mathrm{L}}/{m}_{\mathrm{e}}{\omega}_0c$
, where
![]() ${a}_0$
is the normalized vector potential and
${a}_0$
is the normalized vector potential and
![]() ${E}_{\mathrm{L}}$
is the electric field of the laser) are 0.02 and 0.03, respectively. Other simulation parameters are listed as follows. The electron temperature is
${E}_{\mathrm{L}}$
is the electric field of the laser) are 0.02 and 0.03, respectively. Other simulation parameters are listed as follows. The electron temperature is
![]() ${T}_{\mathrm{e}}=2.5$
keV and the ion temperature is
${T}_{\mathrm{e}}=2.5$
keV and the ion temperature is
![]() ${T}_{\mathrm{i}}=200$
eV. Tritium plasma is used in the simulation and the electron density is
${T}_{\mathrm{i}}=200$
eV. Tritium plasma is used in the simulation and the electron density is
![]() ${n}_{\mathrm{e}}=0.095{n}_{\mathrm{c}}$
. The laser wavelength is
${n}_{\mathrm{e}}=0.095{n}_{\mathrm{c}}$
. The laser wavelength is
![]() ${\lambda}_0=$
351 nm, the laser is propagating in the
${\lambda}_0=$
351 nm, the laser is propagating in the
![]() $x$
direction and its electric field lies in the
$x$
direction and its electric field lies in the
![]() $y$
direction (p-polarized). The simulation box is
$y$
direction (p-polarized). The simulation box is
![]() $120{\lambda}_0\times 40{\lambda}_0$
in the
$120{\lambda}_0\times 40{\lambda}_0$
in the
![]() $x\times y$
directions, and the grid steps are
$x\times y$
directions, and the grid steps are
![]() $0.02{\lambda}_0\times 0.02{\lambda}_0$
in the
$0.02{\lambda}_0\times 0.02{\lambda}_0$
in the
![]() $x\times y$
directions. In each simulation cell, 200 electrons and 200 ions are used. The plasma is located between
$x\times y$
directions. In each simulation cell, 200 electrons and 200 ions are used. The plasma is located between
![]() $x=10{\lambda}_0$
and
$x=10{\lambda}_0$
and
![]() $110{\lambda}_0$
along the
$110{\lambda}_0$
along the
![]() $x$
direction and between
$x$
direction and between
![]() $y=-20{\lambda}_0$
and
$y=-20{\lambda}_0$
and
![]() $y=20{\lambda}_0$
along the
$y=20{\lambda}_0$
along the
![]() $y$
direction. The total simulation time is
$y$
direction. The total simulation time is
![]() $3500{T}_0$
, where
$3500{T}_0$
, where
![]() ${T}_0=c/{\lambda}_0\approx 1.17$
fs is the laser cycle.
${T}_0=c/{\lambda}_0\approx 1.17$
fs is the laser cycle.
Since
![]() ${k}_{\mathrm{epw}}{\lambda}_{\mathrm{d}}$
is a very important parameter, before discussing the simulations, an estimation of the parameter
${k}_{\mathrm{epw}}{\lambda}_{\mathrm{d}}$
is a very important parameter, before discussing the simulations, an estimation of the parameter
![]() ${k}_{\mathrm{epw}}{\lambda}_{\mathrm{d}}$
is given according to the following equations:
${k}_{\mathrm{epw}}{\lambda}_{\mathrm{d}}$
is given according to the following equations:
where
![]() ${\omega}_0=2\pi c/{\lambda}_0$
is the laser frequency,
${\omega}_0=2\pi c/{\lambda}_0$
is the laser frequency,
![]() ${\mathbf{k}}_{\mathrm{L}}$
is the laser wave vector in plasma,
${\mathbf{k}}_{\mathrm{L}}$
is the laser wave vector in plasma,
![]() ${\omega}_{\mathrm{s}}$
is the frequency of the scattered light,
${\omega}_{\mathrm{s}}$
is the frequency of the scattered light,
![]() ${\mathbf{k}}_{\mathrm{s}}$
is the wave vector of the scattered light and
${\mathbf{k}}_{\mathrm{s}}$
is the wave vector of the scattered light and
![]() ${\omega}_{\mathrm{epw}}$
is the frequency of the EPW. Supposing the angle between
${\omega}_{\mathrm{epw}}$
is the frequency of the EPW. Supposing the angle between
![]() ${\mathbf{k}}_{\mathrm{L}}$
and
${\mathbf{k}}_{\mathrm{L}}$
and
![]() ${\mathbf{k}}_{\mathrm{s}}$
is
${\mathbf{k}}_{\mathrm{s}}$
is
![]() $\theta$
(
$\theta$
(
![]() $0\le \theta \le \pi$
), then
$0\le \theta \le \pi$
), then
![]() $\theta =0$
represents forward SRS (FSRS) and
$\theta =0$
represents forward SRS (FSRS) and
![]() $\theta =\pi$
represents BSRS. The theoretical wave numbers for simulation were calculated, as shown in Figure 1. From the above equations,
$\theta =\pi$
represents BSRS. The theoretical wave numbers for simulation were calculated, as shown in Figure 1. From the above equations,
![]() ${k}_{\mathrm{epw}}{\lambda}_{\mathrm{d}}$
is estimated to be 0.35 for BSRS and
${k}_{\mathrm{epw}}{\lambda}_{\mathrm{d}}$
is estimated to be 0.35 for BSRS and
![]() $0.08$
for FSRS. The simulation results are shown in Figures 2–5.
$0.08$
for FSRS. The simulation results are shown in Figures 2–5.

Figure 1 Calculated wave numbers of the scattered lights and EPWs of SRS for
![]() ${n}_{\mathrm{e}}=0.095{n}_{\mathrm{c}}$
and
${n}_{\mathrm{e}}=0.095{n}_{\mathrm{c}}$
and
![]() ${T}_{\mathrm{e}}=2.5$
keV according to Equations (1)–(5). In the figure,
${T}_{\mathrm{e}}=2.5$
keV according to Equations (1)–(5). In the figure,
![]() ${k}_0={\omega}_0/c$
is the laser wave number in vacuum and the laser is propagating in the
${k}_0={\omega}_0/c$
is the laser wave number in vacuum and the laser is propagating in the
![]() ${k}_x$
direction. Both the laser and the scattered light have polarization, which means the direction of their electric fields is parallel to
${k}_x$
direction. Both the laser and the scattered light have polarization, which means the direction of their electric fields is parallel to
![]() ${k}_x-{k}_y$
. When discussing SRS,
${k}_x-{k}_y$
. When discussing SRS,
![]() ${k}_{\mathrm{L}}={k}_{\mathrm{epw}x}+{k}_{\mathrm{s}x}$
and
${k}_{\mathrm{L}}={k}_{\mathrm{epw}x}+{k}_{\mathrm{s}x}$
and
![]() ${k}_{\mathrm{epw}y}+{k}_{\mathrm{s}y}=0$
should be firstly satisfied; two examples are given in this figure, where the magenta is forward SSRS matching and the cyan is backward SSRS matching.
${k}_{\mathrm{epw}y}+{k}_{\mathrm{s}y}=0$
should be firstly satisfied; two examples are given in this figure, where the magenta is forward SSRS matching and the cyan is backward SSRS matching.
3 Analysis of simulation results
Since the p-polarized laser is propagating in the
![]() $x$
direction, it is reasonable to use the electric field component
$x$
direction, it is reasonable to use the electric field component
![]() ${E}_x$
to reflect the information of the electrostatic modes (for side scattering, it also contains information of electromagnetic (EM) modes), such as the EPWs and the magnetic field
${E}_x$
to reflect the information of the electrostatic modes (for side scattering, it also contains information of electromagnetic (EM) modes), such as the EPWs and the magnetic field
![]() ${B}_z$
to reflect the information of the EM modes. However, before discussing the simulation results, differences among the TPD of the backscattered light, SSRS of the laser and filamentation of the EPWs need to be reviewed firstly. It is known that TPD is a process in which a laser decays into two EPWs. In TPD, the matching conditions are
${B}_z$
to reflect the information of the EM modes. However, before discussing the simulation results, differences among the TPD of the backscattered light, SSRS of the laser and filamentation of the EPWs need to be reviewed firstly. It is known that TPD is a process in which a laser decays into two EPWs. In TPD, the matching conditions are
![]() ${\omega}_0={\omega}_{\mathrm{epw1}}+{\omega}_{\mathrm{epw2}}$
and
${\omega}_0={\omega}_{\mathrm{epw1}}+{\omega}_{\mathrm{epw2}}$
and
![]() ${\mathbf{k}}_{\mathrm{L}}={\mathbf{k}}_{\mathrm{epw1}}+{\mathbf{k}}_{\mathrm{epw2}}$
, where (
${\mathbf{k}}_{\mathrm{L}}={\mathbf{k}}_{\mathrm{epw1}}+{\mathbf{k}}_{\mathrm{epw2}}$
, where (
![]() ${\omega}_{\mathrm{epw1}}$
,
${\omega}_{\mathrm{epw1}}$
,
![]() ${\mathbf{k}}_{\mathrm{epw1}}$
), (
${\mathbf{k}}_{\mathrm{epw1}}$
), (
![]() ${\omega}_{\mathrm{epw2}}$
,
${\omega}_{\mathrm{epw2}}$
,
![]() ${\mathbf{k}}_{\mathrm{epw2}}$
) are the frequencies and wave vectors, respectively, of the two TPD-generated EPWs. For the TPD generated by the backscattered light, (
${\mathbf{k}}_{\mathrm{epw2}}$
) are the frequencies and wave vectors, respectively, of the two TPD-generated EPWs. For the TPD generated by the backscattered light, (
![]() ${\omega}_0$
,
${\omega}_0$
,
![]() ${\mathbf{k}}_{\mathrm{L}}$
) should be exchanged with (
${\mathbf{k}}_{\mathrm{L}}$
) should be exchanged with (
![]() ${\omega}_{\mathrm{bs}}$
,
${\omega}_{\mathrm{bs}}$
,
![]() ${\mathbf{k}}_{\mathrm{bs}}$
), where (
${\mathbf{k}}_{\mathrm{bs}}$
), where (
![]() ${\omega}_{\mathrm{bs}}$
,
${\omega}_{\mathrm{bs}}$
,
![]() ${\mathbf{k}}_{\mathrm{bs}}$
) are the frequency and wave vector, respectively, of the backscattered light. In SSRS, where a laser decays into a scattered light and an EPW, the matching conditions of the two daughter waves are
${\mathbf{k}}_{\mathrm{bs}}$
) are the frequency and wave vector, respectively, of the backscattered light. In SSRS, where a laser decays into a scattered light and an EPW, the matching conditions of the two daughter waves are
![]() ${\omega}_0={\omega}_{\mathrm{epw}}+{\omega}_{\mathrm{s}}$
and
${\omega}_0={\omega}_{\mathrm{epw}}+{\omega}_{\mathrm{s}}$
and
![]() ${\mathbf{k}}_{\mathrm{L}}={\mathbf{k}}_{\mathrm{epw}}+{\mathbf{k}}_{\mathrm{s}}$
. Since the matching conditions are different, we can distinguish these two instabilities according to the wave number spectra of the electric or magnetic fields. Before comparing the wave number spectra, we will give some theoretical estimations. Suppose the angle between
${\mathbf{k}}_{\mathrm{L}}={\mathbf{k}}_{\mathrm{epw}}+{\mathbf{k}}_{\mathrm{s}}$
. Since the matching conditions are different, we can distinguish these two instabilities according to the wave number spectra of the electric or magnetic fields. Before comparing the wave number spectra, we will give some theoretical estimations. Suppose the angle between
![]() ${\mathbf{k}}_{\mathrm{L}}$
and
${\mathbf{k}}_{\mathrm{L}}$
and
![]() ${\mathbf{k}}_{\mathrm{s}}$
is
${\mathbf{k}}_{\mathrm{s}}$
is
![]() $\theta$
, both
$\theta$
, both
![]() ${\mathbf{k}}_{\mathrm{s}}$
and
${\mathbf{k}}_{\mathrm{s}}$
and
![]() ${\mathbf{k}}_{\mathrm{epw}}$
for SRS can be numerically calculated according to Equations (1)–(5). With the angle
${\mathbf{k}}_{\mathrm{epw}}$
for SRS can be numerically calculated according to Equations (1)–(5). With the angle
![]() $\theta$
, Equation (4) can be rewritten as
$\theta$
, Equation (4) can be rewritten as
![]() ${k}_{\mathrm{L}}={k}_{\mathrm{epw}x}+{k}_{\mathrm{s}x}$
and
${k}_{\mathrm{L}}={k}_{\mathrm{epw}x}+{k}_{\mathrm{s}x}$
and
![]() ${k}_{\mathrm{epw}y}+{k}_{\mathrm{s}y}=0$
, where
${k}_{\mathrm{epw}y}+{k}_{\mathrm{s}y}=0$
, where
![]() ${k}_{\mathrm{s}x}={k}_{\mathrm{s}}$
cos
${k}_{\mathrm{s}x}={k}_{\mathrm{s}}$
cos
![]() $\theta$
and
$\theta$
and
![]() ${k}_{\mathrm{s}y}={k}_{\mathrm{s}}$
sin
${k}_{\mathrm{s}y}={k}_{\mathrm{s}}$
sin
![]() $\theta$
. For the plasma density and temperature used in our simulations, the calculated results for
$\theta$
. For the plasma density and temperature used in our simulations, the calculated results for
![]() ${\mathbf{k}}_{\mathrm{epw}}=\left({k}_{\mathrm{epw}x},{k}_{\mathrm{epw}y}\right)$
and
${\mathbf{k}}_{\mathrm{epw}}=\left({k}_{\mathrm{epw}x},{k}_{\mathrm{epw}y}\right)$
and
![]() ${\mathbf{k}}_{\mathrm{s}}=\left({k}_{\mathrm{s}x},{k}_{\mathrm{s}y}\right)$
are shown in Figure 1. From this figure we can easily find out different SRS matchings, for example, forward SSRS matching and backward SSRS matching are shown in the figure. Filamentation of the EPW is not a three-wave process, so the wave number matching conditions are not necessarily satisfied. Although the EPW also has transverse components in wave number space (k-space), it is easily distinguished from TPD or SSRS according to the matching conditions.
${\mathbf{k}}_{\mathrm{s}}=\left({k}_{\mathrm{s}x},{k}_{\mathrm{s}y}\right)$
are shown in Figure 1. From this figure we can easily find out different SRS matchings, for example, forward SSRS matching and backward SSRS matching are shown in the figure. Filamentation of the EPW is not a three-wave process, so the wave number matching conditions are not necessarily satisfied. Although the EPW also has transverse components in wave number space (k-space), it is easily distinguished from TPD or SSRS according to the matching conditions.

Figure 2 Snapshots of
![]() ${E}_x$
in k-space for case 1 (a) and case 2 (b) at the early stage (
${E}_x$
in k-space for case 1 (a) and case 2 (b) at the early stage (
![]() $t=500{T}_0$
). Snapshots of
$t=500{T}_0$
). Snapshots of
![]() ${E}_x$
in k-space for case 1 (c) and case 2 (d) at the latter stage (
${E}_x$
in k-space for case 1 (c) and case 2 (d) at the latter stage (
![]() $t=2500{T}_0$
). The intensities of the spectra are in arbitrary units. The arrows denote the excited instabilities and the dashed lines denote the theoretical wave numbers of the EPW (red) and the scattered light (black) shown in Figure 1. It should be mentioned that
$t=2500{T}_0$
). The intensities of the spectra are in arbitrary units. The arrows denote the excited instabilities and the dashed lines denote the theoretical wave numbers of the EPW (red) and the scattered light (black) shown in Figure 1. It should be mentioned that
![]() ${E}_x$
has both an EM component and an electrostatic component for side scattering.
${E}_x$
has both an EM component and an electrostatic component for side scattering.

Figure 3 Snapshots of
![]() ${B}_z$
in k-space: (a), (b) cases 1 and 2, respectively, at
${B}_z$
in k-space: (a), (b) cases 1 and 2, respectively, at
![]() $t=500{T}_0$
; (c), (d) cases 1 and 2, respectively, at
$t=500{T}_0$
; (c), (d) cases 1 and 2, respectively, at
![]() $t=2500{T}_0$
. The magenta dashed curve represents the theoretical wave numbers of back scattered or back side scattered light and the red dashed curve represents the theoretical wave numbers of forward scattered or forward side scattered light. In the figure, the intensities of the spectra are in arbitrary units.
$t=2500{T}_0$
. The magenta dashed curve represents the theoretical wave numbers of back scattered or back side scattered light and the red dashed curve represents the theoretical wave numbers of forward scattered or forward side scattered light. In the figure, the intensities of the spectra are in arbitrary units.
Based on the above analysis, Figure 2 gives four snapshots of the
![]() ${E}_x$
fields in k-space for both cases 1 and 2 to decide what instabilities are excited. Figures 2(a) and 2(b) are
${E}_x$
fields in k-space for both cases 1 and 2 to decide what instabilities are excited. Figures 2(a) and 2(b) are
![]() ${E}_x\left({k}_x,{k}_y\right)$
at
${E}_x\left({k}_x,{k}_y\right)$
at
![]() $t=500{T}_0$
(early stage) and Figures 2(c) and 2(d) are at
$t=500{T}_0$
(early stage) and Figures 2(c) and 2(d) are at
![]() $t=2500{T}_0$
(latter stage). In case 1, the theoretical wave number of the EPW of BSRS is
$t=2500{T}_0$
(latter stage). In case 1, the theoretical wave number of the EPW of BSRS is
![]() ${k}_{\mathrm{bsrs}}\approx 1.514{k}_0$
, where
${k}_{\mathrm{bsrs}}\approx 1.514{k}_0$
, where
![]() ${k}_0={\omega}_0/c$
is the wave number of the laser in vacuum, and the theoretical wave number of the backscattered light is
${k}_0={\omega}_0/c$
is the wave number of the laser in vacuum, and the theoretical wave number of the backscattered light is
![]() ${k}_{\mathrm{bs}}\approx -0.562{k}_0$
. In Figure 2(a), both the signals of TPD and BSRS are observed, but both of them are very weak. The wave numbers of two TPD-generated EPWs are
${k}_{\mathrm{bs}}\approx -0.562{k}_0$
. In Figure 2(a), both the signals of TPD and BSRS are observed, but both of them are very weak. The wave numbers of two TPD-generated EPWs are
![]() ${\mathbf{k}}_{\mathrm{epw1}}/{k}_0=\left(\mathrm{0.221,0.575}\right)$
and
${\mathbf{k}}_{\mathrm{epw1}}/{k}_0=\left(\mathrm{0.221,0.575}\right)$
and
![]() ${\mathbf{k}}_{\mathrm{epw2}}/{k}_0=\left(-0.783,-0.575\right)$
which satisfy the matching condition
${\mathbf{k}}_{\mathrm{epw2}}/{k}_0=\left(-0.783,-0.575\right)$
which satisfy the matching condition
![]() ${\mathbf{k}}_{\mathrm{bs}}={\mathbf{k}}_{\mathrm{epw1}}+{\mathbf{k}}_{\mathrm{epw2}}$
. Furthermore, from Equations (2) and (3), the frequencies are calculated as
${\mathbf{k}}_{\mathrm{bs}}={\mathbf{k}}_{\mathrm{epw1}}+{\mathbf{k}}_{\mathrm{epw2}}$
. Furthermore, from Equations (2) and (3), the frequencies are calculated as
![]() ${\omega}_{\mathrm{bs}}/{\omega}_0\approx 0.641$
,
${\omega}_{\mathrm{bs}}/{\omega}_0\approx 0.641$
,
![]() ${\omega}_{\mathrm{epw1}}/{\omega}_0\approx 0.317$
and
${\omega}_{\mathrm{epw1}}/{\omega}_0\approx 0.317$
and
![]() ${\omega}_{\mathrm{epw2}}/{\omega}_0\approx 0.330$
, which also satisfy the frequency matching condition
${\omega}_{\mathrm{epw2}}/{\omega}_0\approx 0.330$
, which also satisfy the frequency matching condition
![]() ${\omega}_{\mathrm{bs}}={\omega}_{\mathrm{epw1}}+{\omega}_{\mathrm{epw2}}$
with a very small error. However,
${\omega}_{\mathrm{bs}}={\omega}_{\mathrm{epw1}}+{\omega}_{\mathrm{epw2}}$
with a very small error. However,
![]() ${\mathbf{k}}_{\mathrm{epw1}}$
and
${\mathbf{k}}_{\mathrm{epw1}}$
and
![]() ${\mathbf{k}}_{\mathrm{epw2}}$
are not definitely EPW signals because an EM wave also has
${\mathbf{k}}_{\mathrm{epw2}}$
are not definitely EPW signals because an EM wave also has
![]() ${E}_x$
components when it is obliquely propagating. Complementary evidence is that
${E}_x$
components when it is obliquely propagating. Complementary evidence is that
![]() ${B}_z$
in k-space has no such signals, as shown in Figure 3(a), so it is reasonable to conclude that TPD of the backscattered light is excited. In case 2, TPDs of the backscattered light and BSRS also coexist in the early stage, as is shown in Figure 2(b). However, there are several differences between cases 1 and 2. Firstly, the EPW of BSRS is much more intense in case 2, and the frequency (or wave number) of the EPW is broadened in both the
${B}_z$
in k-space has no such signals, as shown in Figure 3(a), so it is reasonable to conclude that TPD of the backscattered light is excited. In case 2, TPDs of the backscattered light and BSRS also coexist in the early stage, as is shown in Figure 2(b). However, there are several differences between cases 1 and 2. Firstly, the EPW of BSRS is much more intense in case 2, and the frequency (or wave number) of the EPW is broadened in both the
![]() ${k}_x$
direction and the
${k}_x$
direction and the
![]() ${k}_y$
direction. Secondly, obliquely propagating EM components with a maximum
${k}_y$
direction. Secondly, obliquely propagating EM components with a maximum
![]() ${k}_x/{k}_0\approx -0.562$
are observed and
${k}_x/{k}_0\approx -0.562$
are observed and
![]() ${B}_x$
in k-space shown in Figure 3(b) further proves they are EM components. Thirdly, the EPWs also possess transverse components and part of them satisfy the wave number matching conditions of SSRS. The theoretical curve shows that backward SSRS (
${B}_x$
in k-space shown in Figure 3(b) further proves they are EM components. Thirdly, the EPWs also possess transverse components and part of them satisfy the wave number matching conditions of SSRS. The theoretical curve shows that backward SSRS (
![]() $\theta >90{}^{\circ}$
) is excited in this stage, which is also proved by Figure 3(b). The unmatched transverse parts are the result of filamentation of the EPWs. A short conclusion for this stage can be made as follows: if the driver of BSRS is relatively weak, the scattered light will excite the TPD and thus mitigate BSRS. However, if the driver is intense enough, the TPD cannot dissipate all energy of the backscattered light, then BSRS and backward SSRS will get an opportunity to grow, and the EPWs generated by them will grow intense enough to excite filamentation instability. In the latter stage (
$\theta >90{}^{\circ}$
) is excited in this stage, which is also proved by Figure 3(b). The unmatched transverse parts are the result of filamentation of the EPWs. A short conclusion for this stage can be made as follows: if the driver of BSRS is relatively weak, the scattered light will excite the TPD and thus mitigate BSRS. However, if the driver is intense enough, the TPD cannot dissipate all energy of the backscattered light, then BSRS and backward SSRS will get an opportunity to grow, and the EPWs generated by them will grow intense enough to excite filamentation instability. In the latter stage (
![]() $t=2500{T}_0$
), the EPWs generated by TPD in case 1 grow larger and the EPW of the BSRS is still strongly mitigated, as is shown in Figure 2(c). In addition, Figure 3(c) shows that there are still no obliquely propagating EM components generated. In case 2, Figure 2(d) shows that the TPD of the backscattered light is suppressed, as well as frequency broadening of the EPW generated by BSRS. SSRS is also observed in Figure 1(d); however, in this stage the theoretical curves shown in Figures 2(d) and 3(d) imply that it is forward SSRS (
$t=2500{T}_0$
), the EPWs generated by TPD in case 1 grow larger and the EPW of the BSRS is still strongly mitigated, as is shown in Figure 2(c). In addition, Figure 3(c) shows that there are still no obliquely propagating EM components generated. In case 2, Figure 2(d) shows that the TPD of the backscattered light is suppressed, as well as frequency broadening of the EPW generated by BSRS. SSRS is also observed in Figure 1(d); however, in this stage the theoretical curves shown in Figures 2(d) and 3(d) imply that it is forward SSRS (
![]() $\theta <90{}^{\circ}$
) now. The unmatched part is also due to filamentation instability. It can be concluded that in the case of a stronger driver, both BSRS and TPD will be suppressed in the latter stage. Instead, FSRS and forward SSRS will grow larger and filamentation instability will be excited.
$\theta <90{}^{\circ}$
) now. The unmatched part is also due to filamentation instability. It can be concluded that in the case of a stronger driver, both BSRS and TPD will be suppressed in the latter stage. Instead, FSRS and forward SSRS will grow larger and filamentation instability will be excited.

Figure 4 Snapshots of
![]() ${E}_x$
in real space, k-space and electron density perturbation
${E}_x$
in real space, k-space and electron density perturbation
![]() $\delta {n}_{\mathrm{e}}/{n}_{\mathrm{c}}={n}_{\mathrm{e}}/{n}_{\mathrm{c}}-0.1028$
in real space. The left column represents the early stage at
$\delta {n}_{\mathrm{e}}/{n}_{\mathrm{c}}={n}_{\mathrm{e}}/{n}_{\mathrm{c}}-0.1028$
in real space. The left column represents the early stage at
![]() $t=500{T}_0$
and the right column represents the latter stage at
$t=500{T}_0$
and the right column represents the latter stage at
![]() $t=2500{T}_0$
. (a), (b)
$t=2500{T}_0$
. (a), (b)
![]() ${E}_x$
in real space, where the value is normalized by
${E}_x$
in real space, where the value is normalized by
![]() ${E}_0=9.16\times {10}^{12}$
W/cm2. (c), (d)
${E}_0=9.16\times {10}^{12}$
W/cm2. (c), (d)
![]() ${E}_x$
in k-space for region I. (e), (f)
${E}_x$
in k-space for region I. (e), (f)
![]() ${E}_x$
in k-space for region II. The intensities of the spectra are in arbitrary units. (g), (h)
${E}_x$
in k-space for region II. The intensities of the spectra are in arbitrary units. (g), (h)
![]() $\delta {n}_{\mathrm{e}}$
in real space.
$\delta {n}_{\mathrm{e}}$
in real space.
Several reasons, such as Langmuir wave collapse and TPMI, could be responsible for filamentation of the EPWs. Langmuir wave collapse is excluded for BSRS because it occurs when
![]() ${k}_{\mathrm{epw}}{\lambda}_{\mathrm{d}}<0.3$
, but in our simulations, the parameter
${k}_{\mathrm{epw}}{\lambda}_{\mathrm{d}}<0.3$
, but in our simulations, the parameter
![]() ${k}_{\mathrm{epw}}{\lambda}_{\mathrm{d}}$
for BSRS is 0.35. However, TPMI should be excluded for FSRS because
${k}_{\mathrm{epw}}{\lambda}_{\mathrm{d}}$
for BSRS is 0.35. However, TPMI should be excluded for FSRS because
![]() ${k}_{\mathrm{epw}}{\lambda}_{\mathrm{d}}$
for FSRS is 0.08 in the simulations. From the above results, the reason why filamentation and side scattering are suppressed by TPD is easily analyzed. Take filamentation, for example. The growth rate of filamentation caused by TPMI is obtained from the formula
${k}_{\mathrm{epw}}{\lambda}_{\mathrm{d}}$
for FSRS is 0.08 in the simulations. From the above results, the reason why filamentation and side scattering are suppressed by TPD is easily analyzed. Take filamentation, for example. The growth rate of filamentation caused by TPMI is obtained from the formula
![]() ${\gamma}_{\mathrm{TP MI}}=\mid \Delta {\omega}_{\mathrm{TP}}/4\mid$
[
Reference Rose
25
], where
${\gamma}_{\mathrm{TP MI}}=\mid \Delta {\omega}_{\mathrm{TP}}/4\mid$
[
Reference Rose
25
], where
![]() ${\omega}_{\mathrm{TP}}=h\left({k}_{\mathrm{epw}}{\lambda}_{\mathrm{d}}\right){\omega}_{\mathrm{b}}$
,
${\omega}_{\mathrm{TP}}=h\left({k}_{\mathrm{epw}}{\lambda}_{\mathrm{d}}\right){\omega}_{\mathrm{b}}$
,
![]() ${\omega}_{\mathrm{b}}={k}_{\mathrm{epw}}{v}_{\mathrm{te}}\sqrt{e\phi /{T}_{\mathrm{e}}}$
is the electron bounce frequency and
${\omega}_{\mathrm{b}}={k}_{\mathrm{epw}}{v}_{\mathrm{te}}\sqrt{e\phi /{T}_{\mathrm{e}}}$
is the electron bounce frequency and
![]() $\phi$
is the potential of the EPW, with
$\phi$
is the potential of the EPW, with
![]() $h<0$
. The TPMI has a larger growth rate with a larger
$h<0$
. The TPMI has a larger growth rate with a larger
![]() ${k}_{\mathrm{epw}}{\lambda}_{\mathrm{d}}$
or a larger
${k}_{\mathrm{epw}}{\lambda}_{\mathrm{d}}$
or a larger
![]() $\mid \phi \mid$
. For case 1, the TPD will dissipate the energy of the backscattered light all the time, which results in a decrease of the EPW intensity. As long as the TPD is not saturated,
$\mid \phi \mid$
. For case 1, the TPD will dissipate the energy of the backscattered light all the time, which results in a decrease of the EPW intensity. As long as the TPD is not saturated,
![]() ${\gamma}_{\mathrm{TPMI}}$
in case 1 is always too small to excite filamentation instability. However, in case 2, since the driver is intense enough, BSRS, FSRS and SSRS have larger growth rates. The backscattered light can grow intense enough to saturate the TPD. When the TPD is saturated, other instabilities will get opportunities to grow and cause nonlinearities.
${\gamma}_{\mathrm{TPMI}}$
in case 1 is always too small to excite filamentation instability. However, in case 2, since the driver is intense enough, BSRS, FSRS and SSRS have larger growth rates. The backscattered light can grow intense enough to saturate the TPD. When the TPD is saturated, other instabilities will get opportunities to grow and cause nonlinearities.

Figure 5 Snapshots of the electron distribution functions in x-px space: (a), (b) distribution functions for case 1 in the early and latter stages, respectively; (c), (d) those for case 2 in the early and latter stages, respectively.
To analyze why TPD is suppressed, we give a more detailed analysis for case 2 in Figure 4. In homogeneous plasmas, SRS is subject to both absolute and convective instability. For BSRS, the scattered light is counter-propagating with the laser, so the EPW near the laser incident side is more amplified and has a higher intensity. For FSRS, the intensity distribution is opposite to that of BSRS because the scattered light has the opposite propagation direction to BSRS. As a result, nonlinearities should be initially excited near the left-hand boundary (defined as region I in this paper, i.e.,
![]() $x/{\lambda}_0<70$
) for BSRS but initially excited near the right-hand boundary (region II, i.e.,
$x/{\lambda}_0<70$
) for BSRS but initially excited near the right-hand boundary (region II, i.e.,
![]() $x/{\lambda}_0>70$
) for FSRS. So, Figures 4(a) and 4(b) show that filaments of the EPW of BSRS are firstly observed in region I in the early stage, but filamentation of the EPW of FSRS is more serious in region II in the latter stage. EPWs of BSRS and FSRS are distinguished by their wavelengths in real space; according to Figure 1, the EPW of BSRS has a shorter wavelength (or larger wave number). In Figures 4(c) and 4(e),
$x/{\lambda}_0>70$
) for FSRS. So, Figures 4(a) and 4(b) show that filaments of the EPW of BSRS are firstly observed in region I in the early stage, but filamentation of the EPW of FSRS is more serious in region II in the latter stage. EPWs of BSRS and FSRS are distinguished by their wavelengths in real space; according to Figure 1, the EPW of BSRS has a shorter wavelength (or larger wave number). In Figures 4(c) and 4(e),
![]() ${E}_x$
values in k-space are given for regions I and II at
${E}_x$
values in k-space are given for regions I and II at
![]() $t=500{T}_0$
, respectively. The results show that TPD is excited only in region II in this stage. The reason is that the EPW of BSRS is intense enough to excite nonlinearities in region I in this stage. Theoretically, the quarter critical density of the backscattered light is about
$t=500{T}_0$
, respectively. The results show that TPD is excited only in region II in this stage. The reason is that the EPW of BSRS is intense enough to excite nonlinearities in region I in this stage. Theoretically, the quarter critical density of the backscattered light is about
![]() $0.1028{n}_{\mathrm{c}}$
in this paper, which means TPD will not be excited when the plasma density exceeds
$0.1028{n}_{\mathrm{c}}$
in this paper, which means TPD will not be excited when the plasma density exceeds
![]() $0.1028{n}_{\mathrm{c}}$
. In region I, Figure 4(g) shows that stronger BSRS and filamentation of the EPW cause larger electron density perturbation, which make the electron density locally exceed
$0.1028{n}_{\mathrm{c}}$
. In region I, Figure 4(g) shows that stronger BSRS and filamentation of the EPW cause larger electron density perturbation, which make the electron density locally exceed
![]() $0.1028{n}_{\mathrm{c}}$
(
$0.1028{n}_{\mathrm{c}}$
(
![]() ${n}_{\mathrm{e}}-0.1028{n}_{\mathrm{c}}>0$
), so TPD is suppressed in region I. In the latter stage, FSRS and forward SSRS grow strong enough to generate nonlinearities in both regions I and II. The wave number spectra shown in Figures 4(d) and 4(f) imply that forward SSRS is mainly excited in region I and filamentation of the EPW of FSRS mainly occurs in region II. As mentioned above, EPW collapse[
Reference Xiao, Liu, Wu, Zheng and He
29
] should be the reason for filamentation because
${n}_{\mathrm{e}}-0.1028{n}_{\mathrm{c}}>0$
), so TPD is suppressed in region I. In the latter stage, FSRS and forward SSRS grow strong enough to generate nonlinearities in both regions I and II. The wave number spectra shown in Figures 4(d) and 4(f) imply that forward SSRS is mainly excited in region I and filamentation of the EPW of FSRS mainly occurs in region II. As mentioned above, EPW collapse[
Reference Xiao, Liu, Wu, Zheng and He
29
] should be the reason for filamentation because
![]() ${k}_{\mathrm{epw}}{\lambda}_{\mathrm{d}}<0.3$
for FSRS. Filamentation of the EPW of FSRS also changes the electron density distribution in region II, which also makes the electron density locally exceed
${k}_{\mathrm{epw}}{\lambda}_{\mathrm{d}}<0.3$
for FSRS. Filamentation of the EPW of FSRS also changes the electron density distribution in region II, which also makes the electron density locally exceed
![]() $0.1028{n}_{\mathrm{c}}$
, as shown in Figure 4(h). As a result, TPD is suppressed in region II in the latter stage, as shown in Figure 4(f).
$0.1028{n}_{\mathrm{c}}$
, as shown in Figure 4(h). As a result, TPD is suppressed in region II in the latter stage, as shown in Figure 4(f).
Distributions of electrons in phase space are employed to reflect the trapping process. In phase space, the trapping structure is a series of ‘phase islands’ with their center near the phase velocity of the EPWs. For the simulation parameters used in this paper, the phase velocity of the EPW is
![]() ${v}_{\mathrm{bs}}/c=0.2369$
for BSRS and
${v}_{\mathrm{bs}}/c=0.2369$
for BSRS and
![]() ${v}_{\mathrm{fs}}/c=0.9281$
for FSRS. The phase velocities of the two EPWs generated by the TPD of the backscattered light are calculated as
${v}_{\mathrm{fs}}/c=0.9281$
for FSRS. The phase velocities of the two EPWs generated by the TPD of the backscattered light are calculated as
![]() ${v}_{\mathrm{ph1}}/c=0.5146$
and
${v}_{\mathrm{ph1}}/c=0.5146$
and
![]() ${v}_{\mathrm{ph2}}/c=0.3397$
according to Figure 2(c), and their
${v}_{\mathrm{ph2}}/c=0.3397$
according to Figure 2(c), and their
![]() $x$
components are
$x$
components are
![]() ${v}_{1x}\approx 0.1846c$
and
${v}_{1x}\approx 0.1846c$
and
![]() ${v}_{2x}\approx 0.2738c$
. As shown in Figures 5(a) and 5(b), in the early stage, the trapping structure is not obvious for case 1 since both TPD and BSRS are not quite intense in this stage. Near the plasma boundary, electrons accelerated by the sheath fields are observed. However, in the latter stage when the EPWs of TPD grow larger, trapping structures for both EPWs are observed in region II (the ‘island’ centers are near their
${v}_{2x}\approx 0.2738c$
. As shown in Figures 5(a) and 5(b), in the early stage, the trapping structure is not obvious for case 1 since both TPD and BSRS are not quite intense in this stage. Near the plasma boundary, electrons accelerated by the sheath fields are observed. However, in the latter stage when the EPWs of TPD grow larger, trapping structures for both EPWs are observed in region II (the ‘island’ centers are near their
![]() $x$
component of the phase velocity). In case 2, Figure 5(c) shows that trapping structures are observed in region I in the early stage. This explains the filamentation of the EPW of BSRS in region I in the early stage. In region II, since BSRS is suppressed, the trapping structure is also suppressed. In the latter stage, Figure 5(d) shows trapping structures with both positive and negative
$x$
component of the phase velocity). In case 2, Figure 5(c) shows that trapping structures are observed in region I in the early stage. This explains the filamentation of the EPW of BSRS in region I in the early stage. In region II, since BSRS is suppressed, the trapping structure is also suppressed. In the latter stage, Figure 5(d) shows trapping structures with both positive and negative
![]() ${p}_x$
. Theoretically, electrons trapped by the EPWs of SRS have only positive
${p}_x$
. Theoretically, electrons trapped by the EPWs of SRS have only positive
![]() ${p}_x$
, as
${p}_x$
, as
![]() ${k}_x$
of the EPWs of SRS are usually positive (see Figure 1). The trapping structure with negative
${k}_x$
of the EPWs of SRS are usually positive (see Figure 1). The trapping structure with negative
![]() ${p}_x$
could be generated by reflection of the EPW on the plasma boundary. On the plasma–vacuum boundaries, strong electrostatic fields (which are named sheath fields) will be generated after a long-term simulation because of charge separation. The sheath field on the right-hand boundary can reflect EPWs, so the abnormal trapping structures in Figure 5(d) are mainly in region II. So, the trapping structures in Figures 5(c) and 5(d) are strong evidences for TPMI.
${p}_x$
could be generated by reflection of the EPW on the plasma boundary. On the plasma–vacuum boundaries, strong electrostatic fields (which are named sheath fields) will be generated after a long-term simulation because of charge separation. The sheath field on the right-hand boundary can reflect EPWs, so the abnormal trapping structures in Figure 5(d) are mainly in region II. So, the trapping structures in Figures 5(c) and 5(d) are strong evidences for TPMI.
4 Discussion and conclusion
It should be mentioned that 3D PIC simulations could be more powerful to research LPIs because more physics are included. For example, in inhomogeneous plasmas, tangential SSRS in which the scattered light is propagating in the
![]() ${k}_z$
direction (Figure 1) has to be investigated by 3D PIC. Filamentation of (EM or electrostatic) waves is also a 3D process; 2D PIC may overestimate its growth rate. However, the computational complexity and cost of 3D simulations increase geometrically compared to 2D simulations. Particularly for our work (both scales of the simulation time and space are too large), the computational complexity and cost of 3D simulations are nearly unacceptable. Fortunately, in this paper TPD and SSRS have the maximum growth rates in the
${k}_z$
direction (Figure 1) has to be investigated by 3D PIC. Filamentation of (EM or electrostatic) waves is also a 3D process; 2D PIC may overestimate its growth rate. However, the computational complexity and cost of 3D simulations increase geometrically compared to 2D simulations. Particularly for our work (both scales of the simulation time and space are too large), the computational complexity and cost of 3D simulations are nearly unacceptable. Fortunately, in this paper TPD and SSRS have the maximum growth rates in the
![]() ${k}_x-{k}_y$
plane, so 2D PIC simulations are enough to investigate their competition.
${k}_x-{k}_y$
plane, so 2D PIC simulations are enough to investigate their competition.
In conclusion, with the help of 2D PIC simulations, we investigate the competition among several instabilities, including TPD, of the backscattered light, filamentation of the EPWs generated by both BSRS and FSRS, and SSRS of the laser. The simulation results show that when the laser intensity is near
![]() ${10}^{15}$
W/cm2 but much smaller than
${10}^{15}$
W/cm2 but much smaller than
![]() ${10}^{16}$
W/cm2, the TPD of the backscattered light is the dominated secondary instability. The TPD will dissipate the energy that suppresses filamentation of both the EPWs and SSRS, as well as BSRS and FSRS. However, when the laser intensity is near or higher than
${10}^{16}$
W/cm2, the TPD of the backscattered light is the dominated secondary instability. The TPD will dissipate the energy that suppresses filamentation of both the EPWs and SSRS, as well as BSRS and FSRS. However, when the laser intensity is near or higher than
![]() ${10}^{16}$
W/cm2, the TPD of the backscattered light is only excited in the early stage (before 1 ps). In the latter stage (after 3 ps) it will be strongly suppressed by increased plasma density perturbation caused by increased EPWs and their nonlinearities. At this time, the suppression of BSRS, FSRS and other nonlinearities will be weakened or even disappear. Deeper analysis shows that filamentation of the EPW of BSRS is caused by TPMI, but filamentation of the EPW of FSRS is caused by EPW collapse. The plasma density used in the simulation is
${10}^{16}$
W/cm2, the TPD of the backscattered light is only excited in the early stage (before 1 ps). In the latter stage (after 3 ps) it will be strongly suppressed by increased plasma density perturbation caused by increased EPWs and their nonlinearities. At this time, the suppression of BSRS, FSRS and other nonlinearities will be weakened or even disappear. Deeper analysis shows that filamentation of the EPW of BSRS is caused by TPMI, but filamentation of the EPW of FSRS is caused by EPW collapse. The plasma density used in the simulation is
![]() $0.095{n}_{\mathrm{c}}$
, which is a common density in gas-filled hohlraums in indirect-drive ICF or the corona plasma in direct-drive ICF. As a result, this research is useful for researchers to obtain a better understanding of LPIs and hot-electron generation in ICF experiments.
$0.095{n}_{\mathrm{c}}$
, which is a common density in gas-filled hohlraums in indirect-drive ICF or the corona plasma in direct-drive ICF. As a result, this research is useful for researchers to obtain a better understanding of LPIs and hot-electron generation in ICF experiments.
Acknowledgements
The authors are grateful to Jiaying Liu, Zhanjun Liu, et al., for plentiful discussions. This research was supported by the National Natural Science Foundation of China (Nos. 12205274, 12275251, 12035002, 11975215).