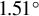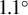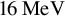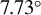1 Introduction
In recent years, laser-driven particle sources, such as electrons[ Reference Gonsalves, Nakamura, Daniels, Benedetti, Pieronek, de Raadt, Steinke, Bin, Bulanov, van Tilborg, Geddes, Schroeder, Toth, Esarey, Swanson, Fan-Chiang, Bagdasarov, Bobrova, Gasilov, Korn, Sasorov and Leemans 1 ], ions[ Reference Macchi, Borghesi and Passoni 2 ] and neutrons[ Reference Gunther, Rosmej, Tavana, Gyrdymov, Skobliakov, Kantsyrev, Zahter, Borisenko, Pukhov and Andreev 3 ], have been greatly developed due to their promising applications in high-energy density physics, nuclear physics, and cancer therapy treatment. Based on laser-accelerated electrons, gamma-ray radiations are also gaining increasing interest due to their ultra-high peak brilliance, short pulse duration and small beam size[ Reference Glinec, Faure, Dain, Darbon, Hosokai, Santos, Lefebvre, Rousseau, Burgy, Mercier and Malka 4 – Reference Sarri, Corvan, Schumaker, Cole, Di Piazza, Ahmed, Harvey, Keitel, Krushelnick, Mangles, Najmudin, Symes, Thomas, Yeung, Zhao and Zepf 7 ]. Such compact gamma-ray sources could pave the way for nuclear photonics, producing ultra-short neutron sources and medical isotopes[ Reference Janek, Svensson, Jonsson and Brahme 8 ], and radiography. In particular, the small beam size and large peak flux of the laser-generated gamma-ray sources can greatly improve the contrast and spatial resolution for nondestructive radiography compared to other approaches[ Reference Kieffer, Krol, Jiang, Chamberlain, Scalzetti and Ichalalene 9 ]. In strong-field quantum-electrodynamics, a promising approach to observe the Breit–Wheeler electron–positron pair production[ Reference Breit and Wheeler 10 ] in the linear or nonlinear regime is to collide laser-driven gamma photons with superintense lasers[ Reference Burke, Field, HortonSmith, Spencer, Walz, Berridge, Bugg, Shmakov, Weidemann, Bula, McDonald, Prebys, Bamber, Boege, Koffas, Kotseroglou, Melissinos, Meyerhofer, Reis and Raggk 11 ], X-ray radiations[ Reference Nousch, Seipt, Kämpfer and Titov 12 ] or with each other. This requires the gamma beams to be collimated, guaranteeing high photon density in the collision region.
There are three main mechanisms to generate gamma-ray beams based on laser-driven energetic electrons in experiments: betatron radiation[
Reference Cipiccia, Islam, Ersfeld, Shanks, Brunetti, Vieux, Yang, Issac, Wiggins, Welsh, Anania, Maneuski, Montgomery, Smith, Hoek, Hamilton, Lemos, Symes, Rajeev, Shea, Dias and Jaroszynski
13
], inverse Compton scattering (ICS)[
Reference Chen, Powers, Ghebregziabher, Maharjan, Liu, Golovin, Banerjee, Zhang, Cunningham, Moorti, Clarke, Pozzi and Umstadter
14
,
Reference Phuoc, Corde, Thaury, Malka, Tafzi, Goddet, Shah, Sebban and Rousse
15
] and bremsstrahlung radiation[
Reference Glinec, Faure, Dain, Darbon, Hosokai, Santos, Lefebvre, Rousseau, Burgy, Mercier and Malka
4
,
Reference Giulietti, Bourgeois, Ceccotti, Davoine, Dobosz, D’Oliveira, Galimberti, Galy, Gamucci, Giulietti, Gizzi, Hamilton, Lefebvre, Labate, Marques, Monot, Popescu, Reau, Sarri, Tomassini and Martin
5
,
Reference Lemos, Albert, Shaw, Papp, Polanek, King, Milder, Marsh, Pak, Pollock, Hegelich, Moody, Park, Tommasini, Williams, Chen and Joshi
16
,
Reference Li, Shen, Xu, Xu, Yu, Li, Lu, Wang, Wang, Liang, Leng, Li and Xu
17
]. In general, betatron radiation produces gamma rays with photon energies from hundreds of keV to MeV when electrons oscillate in the laser-driven plasma bubble field. In ICS, the number of photons obtained by laser photons scattered by high-energy electrons is usually at the
![]() ${10}^7$
level[
Reference Corde, Phuoc, Lambert, Fitour, Malka, Rousse, Beck and Lefebvre
18
], with photon energies up to several tens of MeV and good beam collimation. On the other hand, copious gamma photons can be produced when energetic electrons collide with high atomic-number nuclei through bremsstrahlung radiation. In this case, the maximum energy of the gamma photon is comparable to the maximum electron energy. It is advantageous for producing large photon numbers, up to
${10}^7$
level[
Reference Corde, Phuoc, Lambert, Fitour, Malka, Rousse, Beck and Lefebvre
18
], with photon energies up to several tens of MeV and good beam collimation. On the other hand, copious gamma photons can be produced when energetic electrons collide with high atomic-number nuclei through bremsstrahlung radiation. In this case, the maximum energy of the gamma photon is comparable to the maximum electron energy. It is advantageous for producing large photon numbers, up to
![]() $3.2\times {10}^{10}$
, with a femtosecond laser[
Reference Li, Shen, Xu, Xu, Yu, Li, Lu, Wang, Wang, Liang, Leng, Li and Xu
17
] .
$3.2\times {10}^{10}$
, with a femtosecond laser[
Reference Li, Shen, Xu, Xu, Yu, Li, Lu, Wang, Wang, Liang, Leng, Li and Xu
17
] .
A key to increase the photon yield in bremsstrahlung radiation is enhancing the number of relativistic electrons in laser–plasma accelerations. For instance[
Reference Lemos, Albert, Shaw, Papp, Polanek, King, Milder, Marsh, Pak, Pollock, Hegelich, Moody, Park, Tommasini, Williams, Chen and Joshi
16
], using picosecond laser pulses of relatively high pulse energy, plasma wakefield acceleration in the self-modulated regime produces
![]() $7.5\;\mathrm{nC}$
electrons, hence inducing a photon number of
$7.5\;\mathrm{nC}$
electrons, hence inducing a photon number of
![]() ${10}^9$
photons
${10}^9$
photons
![]() ${\mathrm{keV}}^{-1}\;\mathrm{S}{\mathrm{r}}^{-1}$
. However, the divergence of bremsstrahlung gamma-ray beams is usually quite large (~several tens of degrees)[
Reference Li, Shen, Xu, Xu, Yu, Li, Lu, Wang, Wang, Liang, Leng, Li and Xu
17
] because of the scattering by the nucleus coulomb field.
${\mathrm{keV}}^{-1}\;\mathrm{S}{\mathrm{r}}^{-1}$
. However, the divergence of bremsstrahlung gamma-ray beams is usually quite large (~several tens of degrees)[
Reference Li, Shen, Xu, Xu, Yu, Li, Lu, Wang, Wang, Liang, Leng, Li and Xu
17
] because of the scattering by the nucleus coulomb field.
In this work, to obtain high-yield low-divergence gamma sources, we first produce a collimated high-charge electron beam through picosecond laser-driven self-modulated wakefield acceleration (SM-LWFA). Then it is sent to a high-Z target. The bremsstrahlung gamma-ray photons are measured with a high-resolution Compton-scattering spectrometer (CSS). The latter contains a gradual magnetic field to improve the energy resolution. The measured spectra are reproduced with GEANT4 simulations, suggesting a total photon number of
![]() $2.2\times {10}^{11}$
gamma photons (>
$2.2\times {10}^{11}$
gamma photons (>
![]() $0.3\;\mathrm{MeV}$
) within a divergence angle of
$0.3\;\mathrm{MeV}$
) within a divergence angle of
![]() $7.73{}^{\circ}$
. Such gamma photons are advantageous in radiography, exploring nuclear photonics, strong-field quantum electrodynamics (QED) physics, etc.
$7.73{}^{\circ}$
. Such gamma photons are advantageous in radiography, exploring nuclear photonics, strong-field quantum electrodynamics (QED) physics, etc.
2 Experimental setup
The experiment was carried out on the SG-II UP picosecond experimental platform[
Reference Zhu, Zhu, Li, Zhu, Ma, Lu, Fan, Liu, Zhou, Xu, Zhang, Xie, Yang, Wang, Ouyang, Wang, Li, Yang, Fan, Sun, Liu, Liu, Zhang, Tao, Sun, Zhu, Wang, Jiao, Ren, Liu, Jiao, Huang and Lin
19
] at the Shanghai Institute of Optics and Fine Mechanics (SIOM). A schematic diagram of the experiment is shown in Figure 1. A linearly polarized laser pulse with a pulse duration of
![]() ${\tau}_{\mathrm{p}}=1\;\mathrm{ps}$
, a center wavelength of 1053 nm and an energy of
${\tau}_{\mathrm{p}}=1\;\mathrm{ps}$
, a center wavelength of 1053 nm and an energy of
![]() $120\kern0.24em \mathrm{J}$
was focused
$120\kern0.24em \mathrm{J}$
was focused
![]() $600\;\unicode{x3bc} \mathrm{m}$
above a pulsed nozzle that is employed to produce a high-density argon gas jet by an
$600\;\unicode{x3bc} \mathrm{m}$
above a pulsed nozzle that is employed to produce a high-density argon gas jet by an
![]() $f/2.8$
off-axis parabolic mirror. The focal spot has a full width at half maximum (FWHM) of
$f/2.8$
off-axis parabolic mirror. The focal spot has a full width at half maximum (FWHM) of
![]() $35\;\unicode{x3bc} \mathrm{m}$
, reaching peak intensity of
$35\;\unicode{x3bc} \mathrm{m}$
, reaching peak intensity of
![]() $3.1\times {10}^{18}\;\mathrm{W}/\mathrm{c}{\mathrm{m}}^2$
. The on-target laser field corresponds to a normalized laser amplitude
$3.1\times {10}^{18}\;\mathrm{W}/\mathrm{c}{\mathrm{m}}^2$
. The on-target laser field corresponds to a normalized laser amplitude
![]() $a\approx 2.3$
, where
$a\approx 2.3$
, where
![]() $a= eE/ m\omega c$
,
$a= eE/ m\omega c$
,
![]() $e$
and
$e$
and
![]() $m$
are the electron charge and mass,
$m$
are the electron charge and mass,
![]() $E$
is the electric field,
$E$
is the electric field,
![]() $\omega$
is the laser frequency and
$\omega$
is the laser frequency and
![]() $c$
is the speed of light in vacuum. The back pressure of the argon gas target in the experiment was 17–30 bar, and the optical interferometry of the laser–gas jet interaction indicated that the electron density reached a near-critical density region of (
$c$
is the speed of light in vacuum. The back pressure of the argon gas target in the experiment was 17–30 bar, and the optical interferometry of the laser–gas jet interaction indicated that the electron density reached a near-critical density region of (
![]() $2\hbox{--} 4) \times {10}^{20}\;\mathrm{c}{\mathrm{m}}^{-3}$
, corresponding to a plasma wavelength of
$2\hbox{--} 4) \times {10}^{20}\;\mathrm{c}{\mathrm{m}}^{-3}$
, corresponding to a plasma wavelength of
![]() ${\lambda}_{\mathrm{p}}\approx 1.9\;\unicode{x3bc} \mathrm{m}$
. A
${\lambda}_{\mathrm{p}}\approx 1.9\;\unicode{x3bc} \mathrm{m}$
. A
![]() $2\;\mathrm{mm}$
thick lead target was placed
$2\;\mathrm{mm}$
thick lead target was placed
![]() $2\;\mathrm{mm}$
behind the gas jet. When the laser-accelerated energetic electrons pass through the solid target, they are scattered by the nuclei and emit photons through bremsstrahlung radiation. Electron–positron pair creation through the Bethe–Heitler process[
Reference Xu, Shen, Xu, Li, Yu, Li, Lu, Wang, Wang, Liang, Leng, Li and Xu
20
] also occurs during the interaction process when the emitted photons further interact with nuclei. An electron–positron spectrometer (EPS) with the magnetic field of
$2\;\mathrm{mm}$
behind the gas jet. When the laser-accelerated energetic electrons pass through the solid target, they are scattered by the nuclei and emit photons through bremsstrahlung radiation. Electron–positron pair creation through the Bethe–Heitler process[
Reference Xu, Shen, Xu, Li, Yu, Li, Lu, Wang, Wang, Liang, Leng, Li and Xu
20
] also occurs during the interaction process when the emitted photons further interact with nuclei. An electron–positron spectrometer (EPS) with the magnetic field of
![]() $B=0.8\;\mathrm{T}$
was added
$B=0.8\;\mathrm{T}$
was added
![]() $220\;\mathrm{mm}$
behind the lead target to deflect the positrons and electrons and measure their energy spectra, which had an acceptance divergence angle of
$220\;\mathrm{mm}$
behind the lead target to deflect the positrons and electrons and measure their energy spectra, which had an acceptance divergence angle of
![]() $2.86{}^{\circ}$
. We chose Fuji BAS-SR (or BAS-TR) image plates (IPs) as the recording detector. The IPs were scanned using a GE Typhoon 7000 flatbed IP scanner[Reference Williams, Maddox, Chen, Kojima and Millecchia21].
$2.86{}^{\circ}$
. We chose Fuji BAS-SR (or BAS-TR) image plates (IPs) as the recording detector. The IPs were scanned using a GE Typhoon 7000 flatbed IP scanner[Reference Williams, Maddox, Chen, Kojima and Millecchia21].

Figure 1 Schematic of the experimental setup. (a) A laser pulse propagates through an argon gas target, and energetic electrons are generated and collide with the 2 mm lead target located 2 mm behind the gas target to generate gamma-ray beams. An electron–positron spectrometer (EPS) with an aperture of 10 mm located
![]() $220\;\mathrm{mm}$
behind the lead target with an acceptance divergence angle of
$220\;\mathrm{mm}$
behind the lead target with an acceptance divergence angle of
![]() $2.86{}^{\circ}$
is added to deflect the positrons and electrons and measure their energy spectra. The gamma-ray beam spectra are measured with a typical differential filtering detector (DFD) and a Compton-scattering spectrometer (CSS) with a gradual magnet, which increases linearly along the laser direction and fills the whole spectrometer. The converter target in the CSS is carbon with thickness of 2 mm. The CSS and DFD are added
$2.86{}^{\circ}$
is added to deflect the positrons and electrons and measure their energy spectra. The gamma-ray beam spectra are measured with a typical differential filtering detector (DFD) and a Compton-scattering spectrometer (CSS) with a gradual magnet, which increases linearly along the laser direction and fills the whole spectrometer. The converter target in the CSS is carbon with thickness of 2 mm. The CSS and DFD are added
![]() $500\;\mathrm{mm}$
behind the lead target, which has an acceptance divergence angle of
$500\;\mathrm{mm}$
behind the lead target, which has an acceptance divergence angle of
![]() $1.1{}^{\circ}$
. (b) Trajectories of the converted electron beams dispersed in the gradual magnetic field. These trajectories represent incident electron beams with energies of 0.5–18 MeV. The converted electrons enter the magnetic field with different transverse positions of
$1.1{}^{\circ}$
. (b) Trajectories of the converted electron beams dispersed in the gradual magnetic field. These trajectories represent incident electron beams with energies of 0.5–18 MeV. The converted electrons enter the magnetic field with different transverse positions of
![]() $\left[-5,5\right]\mathrm{mm}$
and different angles of [–
$\left[-5,5\right]\mathrm{mm}$
and different angles of [–
![]() $5{}^{\circ},5{}^{\circ}]$
.
$5{}^{\circ},5{}^{\circ}]$
.
One key aspect of our experiments is the measurement of the gamma-ray spectrum. Gamma-ray beams driven by laser-accelerated electrons are of short pulse duration, comparable to that of the laser pulse (~1 ps here). Conventional scintillation and semiconductor detectors are not applicable to resolve the energy spectrum of the gamma-ray flash since all photons reach the detector in a short instance, resulting in the integrated photon energy being the sum of all received gamma-ray beam energy. Therefore, methods such as Compton scattering[ Reference Corvan, Sarri and Zepf 22 , Reference Zhang, Yang, Hu, Li, Luo, An and Zheng 23 ], photonuclear activation[ Reference Leemans, Rodgers, Catravas, Geddes, Fubiani, Esarey, Shadwick, Donahue and Smith 24 , Reference Günther, Sonnabend, Brambrink, Vogt, Bagnoud, Harres and Roth 25 ] and differential filtering[ Reference Chen, King, Key, Akli, Beg, Chen, Freeman, Link, Mackinnon, MacPhee, Patel, Porkolab, Stephens and Van Woerkom 26 , Reference Nolte, Behrens, Schnurer, Rousse and Ambrosi 27 ] are employed to detect ultra-short gamma-ray flashes. The neutron separation thresholds relevant to the photonuclear activation cover a wide energy range[ Reference Günther, Sonnabend, Brambrink, Vogt, Bagnoud, Harres and Roth 25 ], while the attenuation coefficients are not so sensitive to gamma energy above 2 MeV in differential filtering[ Reference Hubbell, Gimm and Øverbø 28 ]. Thus, their spectrum resolutions are limited, especially in the high-energy region.
In this experiment, we chose a differential filtering detector (DFD) and a CSS together to detect these photons. A typical CSS usually uses a uniform magnetic field profile[
Reference Corvan, Sarri and Zepf
22
] or a stepped magnetic field profile[
Reference Zhang, Yang, Hu, Li, Luo, An and Zheng
23
] to deflect the photon-induced electron–positron pairs. The latter employs a curved surface plate to improve the energy resolution. Instead, we apply a gradual magnetic field for CSS, which increases linearly along the laser direction and fills the whole spectrometer. Thus, it is capable of gathering the converted electrons with the same energy but different emitting angles together and enhances the energy resolution of the gamma-ray beam, as shown in Figure 1(b). There is the electron–positron pair effect in the MeV gamma-ray range. The influence of the electron–positron pair effect can be largely eliminated through their mutual cancellation by the adoption of a symmetrical design for the spectrometer such that the positron and electron spectra are measured simultaneously. Then the energy spectrum of gamma beams can be obtained from the corrected converted electron energy spectrum. The DFD is placed behind the CSS, which consists of 13 pieces of lead filters with dimensions of
![]() $2.5\;\mathrm{cm}\times 2.5\;\mathrm{cm}$
and different thicknesses in the range of 3–10 mm, placed one by one in the beam path, as shown in Figure 1(a). The gamma-ray beam spectrum is calculated using the gamma-ray signal in each IP, considering the lead filter thickness and the attenuation coefficients of these 13 energy groups. We use equation
$2.5\;\mathrm{cm}\times 2.5\;\mathrm{cm}$
and different thicknesses in the range of 3–10 mm, placed one by one in the beam path, as shown in Figure 1(a). The gamma-ray beam spectrum is calculated using the gamma-ray signal in each IP, considering the lead filter thickness and the attenuation coefficients of these 13 energy groups. We use equation
![]() ${D}_i={\Sigma}_j^n{R}_{ij}{\Phi}_j,i=1,2,\cdots, 13$
to calculate the gamma-ray beam spectrum, where
${D}_i={\Sigma}_j^n{R}_{ij}{\Phi}_j,i=1,2,\cdots, 13$
to calculate the gamma-ray beam spectrum, where
![]() ${D}_i$
represents the energy deposition on the ith channel detector,
${D}_i$
represents the energy deposition on the ith channel detector,
![]() ${\Phi}_j$
is the photon number in the jth energy interval, n is the number of filters and
${\Phi}_j$
is the photon number in the jth energy interval, n is the number of filters and
![]() ${R}_{ij}$
is the energy deposition coefficient of photons in the jth energy interval on the ith filter. The CSS and DFD are added
${R}_{ij}$
is the energy deposition coefficient of photons in the jth energy interval on the ith filter. The CSS and DFD are added
![]() $500\;\mathrm{mm}$
behind the lead target, which has an acceptance divergence angle of
$500\;\mathrm{mm}$
behind the lead target, which has an acceptance divergence angle of
![]() $1.1{}^{\circ}$
. In addition, the CSS and DFD are shielded by lead boxes with thicknesses of 1 and
$1.1{}^{\circ}$
. In addition, the CSS and DFD are shielded by lead boxes with thicknesses of 1 and
![]() $2\;\mathrm{cm}$
to avoid the background radiation. Thus, the spectrometers measure the gamma-ray photon signal with low noise.
$2\;\mathrm{cm}$
to avoid the background radiation. Thus, the spectrometers measure the gamma-ray photon signal with low noise.
3 Experimental results and discussion
When a high-intensity
![]() $a>1$
laser pulse with pulse duration
$a>1$
laser pulse with pulse duration
![]() ${\tau}_{\mathrm{p}}$
larger than the plasma period
${\tau}_{\mathrm{p}}$
larger than the plasma period
![]() ${\lambda}_{\mathrm{p}}/ c$
propagates through an underdense plasma
${\lambda}_{\mathrm{p}}/ c$
propagates through an underdense plasma
![]() ${n}_{\mathrm{e}}<{n}_{\mathrm{c}}$
, it undergoes self-focusing and drives plasma waves through the Raman forward scattering (RFS) and self-modulation instabilities[
Reference Lemos, Albert, Shaw, Papp, Polanek, King, Milder, Marsh, Pak, Pollock, Hegelich, Moody, Park, Tommasini, Williams, Chen and Joshi
16
]. The gas target is ionized simultaneously and a significant number of electrons are injected and accelerated. In our case, an argon cluster target with high density is employed to enhance the beam charge of energetic electrons from laser-driven electron acceleration[
Reference Chen, Yan, Li, Hu, Zhang, Wang, Hafz, Mao, Huang, Ma, Zhao, Ma, Li, Lu, Sheng and Wei
29
]. The raw-data recorded by the EPS in Figure 2(a) show that the electron bunch has a broad energy spectrum with a cut-off energy of
${n}_{\mathrm{e}}<{n}_{\mathrm{c}}$
, it undergoes self-focusing and drives plasma waves through the Raman forward scattering (RFS) and self-modulation instabilities[
Reference Lemos, Albert, Shaw, Papp, Polanek, King, Milder, Marsh, Pak, Pollock, Hegelich, Moody, Park, Tommasini, Williams, Chen and Joshi
16
]. The gas target is ionized simultaneously and a significant number of electrons are injected and accelerated. In our case, an argon cluster target with high density is employed to enhance the beam charge of energetic electrons from laser-driven electron acceleration[
Reference Chen, Yan, Li, Hu, Zhang, Wang, Hafz, Mao, Huang, Ma, Zhao, Ma, Li, Lu, Sheng and Wei
29
]. The raw-data recorded by the EPS in Figure 2(a) show that the electron bunch has a broad energy spectrum with a cut-off energy of
![]() $80\;\mathrm{MeV}$
. After the deconvolution[
Reference Bonnet, Comet, Denis-Petit, Gobet, Hannachi, Tarisien, Versteegen and Aleonard
30
], the electron spectrum is plotted as shown in Figure 2(b). The electrons are first accelerated by the longitudinal field, while the transverse field leads to betatron-like oscillations of the off-axis electrons. This transverse electric field of the laser, when in near resonance with the betatron motion of the electrons, will in turn increase the transverse momentum of the electrons, which can be converted into longitudinal momentum via the
v
×
B
force. This process is analogous to the direct laser acceleration (DLA)[
Reference Shaw, Romo-Gonzalez, Lemos, King, Bruhaug, Miller, Dorrer, Kruschwitz, Waxer, Williams, Ambat, McKie, Sinclair, Mori, Joshi, Chen, Palastro, Albert and Froula
31
]. The black line in Figure 2 represents the geometric mean value of the data. It is noted that the electrons accelerated in the plasma wave also undergo betatron oscillations about the laser axis due to the restoring force of the ion column that forms behind the drive laser[
Reference Lemos, Albert, Shaw, Papp, Polanek, King, Milder, Marsh, Pak, Pollock, Hegelich, Moody, Park, Tommasini, Williams, Chen and Joshi
16
]. However, most of the radiation from betatron oscillations cannot pass through the thick lead target in the experiment.
$80\;\mathrm{MeV}$
. After the deconvolution[
Reference Bonnet, Comet, Denis-Petit, Gobet, Hannachi, Tarisien, Versteegen and Aleonard
30
], the electron spectrum is plotted as shown in Figure 2(b). The electrons are first accelerated by the longitudinal field, while the transverse field leads to betatron-like oscillations of the off-axis electrons. This transverse electric field of the laser, when in near resonance with the betatron motion of the electrons, will in turn increase the transverse momentum of the electrons, which can be converted into longitudinal momentum via the
v
×
B
force. This process is analogous to the direct laser acceleration (DLA)[
Reference Shaw, Romo-Gonzalez, Lemos, King, Bruhaug, Miller, Dorrer, Kruschwitz, Waxer, Williams, Ambat, McKie, Sinclair, Mori, Joshi, Chen, Palastro, Albert and Froula
31
]. The black line in Figure 2 represents the geometric mean value of the data. It is noted that the electrons accelerated in the plasma wave also undergo betatron oscillations about the laser axis due to the restoring force of the ion column that forms behind the drive laser[
Reference Lemos, Albert, Shaw, Papp, Polanek, King, Milder, Marsh, Pak, Pollock, Hegelich, Moody, Park, Tommasini, Williams, Chen and Joshi
16
]. However, most of the radiation from betatron oscillations cannot pass through the thick lead target in the experiment.

Figure 2 (a) Raw signal of the laser-accelerated electron beam recorded in the IP. (b) Extracted energy spectrum of the energetic electron beam. The black line represents the geometric mean value of the data of two shots. The shaded region represents uncertainty.
Removing the lead target and spectrometers, a spatial high-energy electron beam analyzer (SHEEBA)[
Reference Galimberti, Giulietti, Giulietti and Gizzi
32
] composed of Al plates and IPs is located
![]() $500\;\mathrm{mm}$
behind the argon target to detect the spatial distribution of the electrons. Figure 3(a) shows a spatial profile of the electrons with energy of more than
$500\;\mathrm{mm}$
behind the argon target to detect the spatial distribution of the electrons. Figure 3(a) shows a spatial profile of the electrons with energy of more than
![]() $2.2\;\mathrm{MeV}$
, blocked by a 5-mm-thick Al plate in front. It has a Gaussian-type distribution with horizontal divergence of
$2.2\;\mathrm{MeV}$
, blocked by a 5-mm-thick Al plate in front. It has a Gaussian-type distribution with horizontal divergence of
![]() $1.51{}^{\circ}$
and vertical divergence of
$1.51{}^{\circ}$
and vertical divergence of
![]() $2.59{}^{\circ}$
for shot 4. The spatial distribution of the electrons seems to be elliptic, almost the same direction as laser polarization, which could be attributed to the residual transverse momentum[
Reference Lemos, Albert, Shaw, Papp, Polanek, King, Milder, Marsh, Pak, Pollock, Hegelich, Moody, Park, Tommasini, Williams, Chen and Joshi
16
,
Reference Thaury, Guillaume, Corde, Lehe, Le Bouteiller, Phuoc, Davoine, Rax, Rousse and Malka
33
] that the electrons gain at the moment of ionization and/or to DLA[
Reference Shaw, Lemos, Amorim, Vafaei-Najafabadi, Marsh, Tsung, Mori and Joshi
34
,
Reference Mangles, Thomas, Kaluza, Lundh, Lindau, Persson, Tsung, Najmudin, Mori, Wahlstrom and Krushelnick
35
]. The divergence angle of the electron beam increases while the energy increases from
$2.59{}^{\circ}$
for shot 4. The spatial distribution of the electrons seems to be elliptic, almost the same direction as laser polarization, which could be attributed to the residual transverse momentum[
Reference Lemos, Albert, Shaw, Papp, Polanek, King, Milder, Marsh, Pak, Pollock, Hegelich, Moody, Park, Tommasini, Williams, Chen and Joshi
16
,
Reference Thaury, Guillaume, Corde, Lehe, Le Bouteiller, Phuoc, Davoine, Rax, Rousse and Malka
33
] that the electrons gain at the moment of ionization and/or to DLA[
Reference Shaw, Lemos, Amorim, Vafaei-Najafabadi, Marsh, Tsung, Mori and Joshi
34
,
Reference Mangles, Thomas, Kaluza, Lundh, Lindau, Persson, Tsung, Najmudin, Mori, Wahlstrom and Krushelnick
35
]. The divergence angle of the electron beam increases while the energy increases from
![]() $E>9.2\;\mathrm{MeV}$
to
$E>9.2\;\mathrm{MeV}$
to
![]() $E>15\;\mathrm{MeV}$
, as shown in Figures 3(b) and 3(c). Electron beam divergence angles of four continuous shots show good stability in Figure 3(d), where the blue and red lines indicate the horizontal and vertical divergence angles, respectively. An electron beam charge of
$E>15\;\mathrm{MeV}$
, as shown in Figures 3(b) and 3(c). Electron beam divergence angles of four continuous shots show good stability in Figure 3(d), where the blue and red lines indicate the horizontal and vertical divergence angles, respectively. An electron beam charge of
![]() $26\;\mathrm{nC}$
is measured here, which is beneficial to the subsequent applications. Detailed analysis of the generated electron beams will appear elsewhere. Such high-charge electron beams have also been obtained by a picosecond-scale[
Reference Shaw, Romo-Gonzalez, Lemos, King, Bruhaug, Miller, Dorrer, Kruschwitz, Waxer, Williams, Ambat, McKie, Sinclair, Mori, Joshi, Chen, Palastro, Albert and Froula
31
] kilojoule-class laser, where the total charge in the electron beams exceeds
$26\;\mathrm{nC}$
is measured here, which is beneficial to the subsequent applications. Detailed analysis of the generated electron beams will appear elsewhere. Such high-charge electron beams have also been obtained by a picosecond-scale[
Reference Shaw, Romo-Gonzalez, Lemos, King, Bruhaug, Miller, Dorrer, Kruschwitz, Waxer, Williams, Ambat, McKie, Sinclair, Mori, Joshi, Chen, Palastro, Albert and Froula
31
] kilojoule-class laser, where the total charge in the electron beams exceeds
![]() $700\;\mathrm{nC}$
and scales approximately linearly with the laser intensity.
$700\;\mathrm{nC}$
and scales approximately linearly with the laser intensity.

Figure 3 (a)–(c) Spatial distribution of the electron beam recorded in the IP corresponding to different energies, namely,
![]() $E>2.2$
MeV, E > 9.2 MeV and E > 15 MeV. (d) Electron beam divergence angles of four continuous shots. The blue and red lines represent horizontal and vertical divergence angles, respectively.
$E>2.2$
MeV, E > 9.2 MeV and E > 15 MeV. (d) Electron beam divergence angles of four continuous shots. The blue and red lines represent horizontal and vertical divergence angles, respectively.
These electrons with nC of charge and low divergence then collide with the 2-mm-thick lead target to generate gamma-ray photons through bremsstrahlung radiation. The EPS serves to remove the secondary electrons and positrons leaving the converting target here. The raw-data recorded by the DFD are shown in Figure 4(a) within the acceptance angle
![]() $1.1{}^{\circ}$
. The spectrum of the gamma-ray beam shows a two-temperature structure (
$1.1{}^{\circ}$
. The spectrum of the gamma-ray beam shows a two-temperature structure (
![]() $0.6$
and
$0.6$
and
![]() $4.4\;\mathrm{MeV}$
). It should also be noticed that the gamma-ray signal on the sixth IP is still clear enough after penetrating a 3.8-cm-thick lead-layer. With a 3-mm-thick lead layer in front of the first IP in Figure 4(a) to block gamma-ray beams with energy lower than
$4.4\;\mathrm{MeV}$
). It should also be noticed that the gamma-ray signal on the sixth IP is still clear enough after penetrating a 3.8-cm-thick lead-layer. With a 3-mm-thick lead layer in front of the first IP in Figure 4(a) to block gamma-ray beams with energy lower than
![]() $0.3\;\mathrm{MeV}$
, a high total photon number of
$0.3\;\mathrm{MeV}$
, a high total photon number of
![]() $2.2\times {10}^9$
is detected by the DFD. The raw-data of positrons and electrons recorded by the CSS are shown in Figures 4(b) and 4(c). The continuous gamma-ray beam spectrum of the geometric mean is shown in Figure 4(d) by a black line, which is in good agreement with the result from the DFD and has a higher energy resolution.
$2.2\times {10}^9$
is detected by the DFD. The raw-data of positrons and electrons recorded by the CSS are shown in Figures 4(b) and 4(c). The continuous gamma-ray beam spectrum of the geometric mean is shown in Figure 4(d) by a black line, which is in good agreement with the result from the DFD and has a higher energy resolution.

Figure 4 (a) Raw-data of the gamma-photon signal recorded by the DFD. Raw-data of positrons (b) and electrons (c) recorded by the CSS. (d) Experimental spectra from the CSS (black solid), the DFD (red cross) and GEANT4 simulation with the experimental electrons as input (blue solid), within the divergence angle of
![]() $1.1{}^{\circ}$
. These horizontal error bars represent 13 energy intervals and the vertical error bars represent uncertainty for the DFD. The black line represents the geometric mean value of the data and the shaded region represents uncertainty for the CSS.
$1.1{}^{\circ}$
. These horizontal error bars represent 13 energy intervals and the vertical error bars represent uncertainty for the DFD. The black line represents the geometric mean value of the data and the shaded region represents uncertainty for the CSS.
To model the gamma-ray generation process, a series of test particle simulations are carried out with the Monte Carlo code GEANT4[
Reference Agostinelli, Allison, Amako, Apostolakis, Araujo, Arce, Asai, Axen, Banerjee, Barrand, Behner, Bellagamba, Boudreau, Broglia, Brunengo, Burkhardt, Chauvie, Chuma, Chytracek, Cooperman, Cosmo, Degtyarenko, Dell’Acqua, Depaola, Dietrich, Enami, Feliciello, Ferguson, Fesefeldt, Folger, Foppiano, Forti, Garelli, Giani, Giannitrapani, Gibin, Gómez Cadenas, González, Gracia Abril, Greeniaus, Greiner, Grichine, Grossheim, Guatelli, Gumplinger, Hamatsu, Hashimoto, Hasui, Heikkinen, Howard, Ivanchenko, Johnson, Jones, Kallenbach, Kanaya, Kawabata, Kawabata, Kawaguti, Kelner, Kent, Kimura, Kodama, Kokoulin, Kossov, Kurashige, Lamanna, Lampén, Lara, Lefebure, Lei, Liendl, Lockman, Longo, Magni, Maire, Medernach, Minamimoto, de Freitas, Morita, Murakami, Nagamatu, Nartallo, Nieminen, Nishimura, Ohtsubo, Okamura, O’Neale, Oohata, Paech, Perl, Pfeiffer, Pia, Ranjard, Rybin, Sadilov, Di Salvo, Santin, Sasaki, Savvas, Sawada, Scherer, Sei, Sirotenko, Smith, Starkov, Stoecker, Sulkimo, Takahata, Tanaka, Tcherniaev, Tehrani, Tropeano, Truscott, Uno, Urban, Urban, Verderi, Walkden, Wander, Weber, Wellisch, Wenaus, Williams, Wright, Yamada, Yoshida and Zschiesche
36
]. The simulation includes several physical processes, such as bremsstrahlung, scattering, ionization, pair production, photoelectric effect and Compton scattering. A total of
![]() ${10}^7$
electrons with the same energy and spatial distributions as the experimental measurement in Figures 2 and 3 impact a 2-mm-thick lead target. The electron source is considered to be point-like. The simulated gamma-ray beam spectrum is shown by the blue line in Figure 4(d), and it is in good agreement with the experimental result, especially in the energy range above
${10}^7$
electrons with the same energy and spatial distributions as the experimental measurement in Figures 2 and 3 impact a 2-mm-thick lead target. The electron source is considered to be point-like. The simulated gamma-ray beam spectrum is shown by the blue line in Figure 4(d), and it is in good agreement with the experimental result, especially in the energy range above
![]() $2.5\;\mathrm{MeV}$
. The simulated temperatures of the gamma-ray beam within
$2.5\;\mathrm{MeV}$
. The simulated temperatures of the gamma-ray beam within
![]() $1.1{}^{\circ}$
are found to be
$1.1{}^{\circ}$
are found to be
![]() $0.9\;\mathrm{MeV}$
for the low-energy part and
$0.9\;\mathrm{MeV}$
for the low-energy part and
![]() $2.7\;\mathrm{MeV}$
for the high-energy part. The slight difference for the low-energy part from the experimental result has not been clarified, and further work is needed. Simulations also indicate that the produced gamma-ray source has an FWHM size of
$2.7\;\mathrm{MeV}$
for the high-energy part. The slight difference for the low-energy part from the experimental result has not been clarified, and further work is needed. Simulations also indicate that the produced gamma-ray source has an FWHM size of
![]() $433\;\unicode{x3bc} \mathrm{m}$
at the emergent surface of the lead converter.
$433\;\unicode{x3bc} \mathrm{m}$
at the emergent surface of the lead converter.
The simulated angular divergences of gamma-ray beams with different energies are summarized in Figure 5(a). It can be seen that the FWHM divergence of the gamma-ray beam of more than
![]() $0.3\;\mathrm{MeV}$
is only
$0.3\;\mathrm{MeV}$
is only
![]() $7.73{}^{\circ}$
, which is lower than the recent experimental results under commensurate laser conditions[
Reference Lemos, Albert, Shaw, Papp, Polanek, King, Milder, Marsh, Pak, Pollock, Hegelich, Moody, Park, Tommasini, Williams, Chen and Joshi
16
]. Considering that the gamma-ray beam has a 2D Gaussian distribution, the acceptance angle of
$7.73{}^{\circ}$
, which is lower than the recent experimental results under commensurate laser conditions[
Reference Lemos, Albert, Shaw, Papp, Polanek, King, Milder, Marsh, Pak, Pollock, Hegelich, Moody, Park, Tommasini, Williams, Chen and Joshi
16
]. Considering that the gamma-ray beam has a 2D Gaussian distribution, the acceptance angle of
![]() $1.1{}^{\circ}$
in the experiment means that only
$1.1{}^{\circ}$
in the experiment means that only
![]() $1\%$
of the photons are measured. Therefore, the total photon number generated in the experiment is estimated to be
$1\%$
of the photons are measured. Therefore, the total photon number generated in the experiment is estimated to be
![]() $2.2\times {10}^{11}$
among the highest yield comparing to previous results[
Reference Lemos, Albert, Shaw, Papp, Polanek, King, Milder, Marsh, Pak, Pollock, Hegelich, Moody, Park, Tommasini, Williams, Chen and Joshi
16
,
Reference Li, Shen, Xu, Xu, Yu, Li, Lu, Wang, Wang, Liang, Leng, Li and Xu
17
,
Reference Döpp, Guillaume, Thaury, Lifschitz, Sylla, Goddet, Tafzi, Iaquanello, Lefrou, Rousseau, Conejero, Ruiz, Phuoc and Malka
37
] driven by laser-accelerated electrons. It is noted that the gamma-ray photon number could be further increased by raising the picosecond-scale laser energy[
Reference Shaw, Romo-Gonzalez, Lemos, King, Bruhaug, Miller, Dorrer, Kruschwitz, Waxer, Williams, Ambat, McKie, Sinclair, Mori, Joshi, Chen, Palastro, Albert and Froula
31
]. The divergence of the gamma-ray beam decreases with the increase of energy, as shown in Figure 5(a). Overall, the gamma-ray beam with high yield and low divergence produced in our experiment could be a promising source for electron–positron production, radiography measurements in high energy density physics (HEDP) and inertial confinement fusion (ICF), and nuclear photonics.
$2.2\times {10}^{11}$
among the highest yield comparing to previous results[
Reference Lemos, Albert, Shaw, Papp, Polanek, King, Milder, Marsh, Pak, Pollock, Hegelich, Moody, Park, Tommasini, Williams, Chen and Joshi
16
,
Reference Li, Shen, Xu, Xu, Yu, Li, Lu, Wang, Wang, Liang, Leng, Li and Xu
17
,
Reference Döpp, Guillaume, Thaury, Lifschitz, Sylla, Goddet, Tafzi, Iaquanello, Lefrou, Rousseau, Conejero, Ruiz, Phuoc and Malka
37
] driven by laser-accelerated electrons. It is noted that the gamma-ray photon number could be further increased by raising the picosecond-scale laser energy[
Reference Shaw, Romo-Gonzalez, Lemos, King, Bruhaug, Miller, Dorrer, Kruschwitz, Waxer, Williams, Ambat, McKie, Sinclair, Mori, Joshi, Chen, Palastro, Albert and Froula
31
]. The divergence of the gamma-ray beam decreases with the increase of energy, as shown in Figure 5(a). Overall, the gamma-ray beam with high yield and low divergence produced in our experiment could be a promising source for electron–positron production, radiography measurements in high energy density physics (HEDP) and inertial confinement fusion (ICF), and nuclear photonics.

Figure 5 (a) The divergence of gamma-ray beam by GEANT4 simulation with energy
![]() $>0.3\;\mathrm{MeV},>1\;\mathrm{MeV}\;\mathrm{and}>2.2\;\mathrm{MeV}$
. (b) Gamma-ray photon (
$>0.3\;\mathrm{MeV},>1\;\mathrm{MeV}\;\mathrm{and}>2.2\;\mathrm{MeV}$
. (b) Gamma-ray photon (
![]() $>0.3\;\mathrm{MeV}$
) yields and divergence (FWHM) versus different lead thicknesses. The simulation is performed with the experimental electrons as input.
$>0.3\;\mathrm{MeV}$
) yields and divergence (FWHM) versus different lead thicknesses. The simulation is performed with the experimental electrons as input.
The influence of thicknesses and the FWHM have also been studied by simulation, as shown in Figure 5(b). At the target thickness, the generated gamma-ray photon number increases due to continuous interaction between the electrons and the target. However, the energetic photons will be attenuated as the target thickness further increases. When these two processes reach a balance, the largest yield of gamma photons is obtained with the lead target thickness of
![]() $4\;\mathrm{mm}$
. The divergence angle of the gamma beams is basically unchanged while the target thickness increases.
$4\;\mathrm{mm}$
. The divergence angle of the gamma beams is basically unchanged while the target thickness increases.
4 Conclusion
In conclusion, we use a picosecond laser to generate electron beams with large charge and low divergence, and subsequently to generate gamma-ray beams with high yield and low divergence through bremsstrahlung radiation. A typical DFD and a specially designed high detection resolution CSS with a gradual magnetic field are used at the same time to detect the generated gamma-ray beams precisely. The gamma-ray beams have a total photon number of
![]() $2.2\times {10}^{11}$
, size of 433 μm and divergence of
$2.2\times {10}^{11}$
, size of 433 μm and divergence of
![]() $7.73{}^{\circ}$
, which make them promising sources for photonuclear reaction and clinical applications. Future improvements on these sources can be done by using higher laser energies.
$7.73{}^{\circ}$
, which make them promising sources for photonuclear reaction and clinical applications. Future improvements on these sources can be done by using higher laser energies.
Acknowledgments
This work was supported by the National Key R&D Program of China (No. 2018YFA0404803), the National Natural Science Foundation of China (Nos. 12175299, 11905278, 11975302, and 11935008), the CAS Project for Young Scientists in Basic Research (No. YSBR060) and the Youth Innovation Promotion Association of Chinese Academy of Sciences (No. 2021242).