Hostname: page-component-84b7d79bbc-g78kv Total loading time: 0 Render date: 2024-07-31T07:18:19.788Z Has data issue: false hasContentIssue false
  • English
  • Français

Totally real surfaces of the six-dimensional sphere

Published online by Cambridge University Press:  18 May 2009

M. A. Bashir
M. A. Bashir
Affiliation:
Department of Mathematics, College of Science, King Saud University, P.O. Box 2455, Riyadh 11451, Saudi Arabia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An almost Hermitian manifold (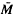, J, g) with Riemannian connection 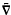is called nearly Kaehlerian if (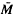xJ)X = 0 for any 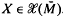. The typical example is the sphere S6. The nearly Kaehlerian structure J for S6 is constructed in a natural way by making use of Cayley division algebra [3]. It is because of this nearly Kaehler, non-Kaehler, structure that S6 has attracted attention. Different classes of submanifolds of S6 have been considered by A. Gray [4], K. Sekigawa [5] and N. Ejiri [2]. In this paper we study 2-dimensional totally real submanifolds of S6. These are submanifolds with the property that for every x є M, J (Tx M) belongs to the normal bundle v. For this class we have obtained the following result.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 33 , Issue 1 , January 1991 , pp. 83 - 87
Copyright
Copyright © Glasgow Mathematical Journal Trust 1991

References

REFERENCES

1.Dillen, F., Verstraelen, L. and Vrancken, L., Classification of totally real 3-dimensional submanifolds of s 6(1) with K ≥ , preprint.Google Scholar
2.Ejiri, N., Totally real submanifolds in a 6-sphere, Proc. Amer. Math. Soc. 83 (1981), 759–763.CrossRefGoogle Scholar
3.Fukami, T. and Ishihara, S., Almost Hermitian structure on S 6, Tohoku Math. J. 7 (1955), 151–156.CrossRefGoogle Scholar
4.Gray, A., Almost complex submanifolds of the six sphere, Proc. Amer. Math. Soc. 20 (1969), 277–279.CrossRefGoogle Scholar
5.Sekigawa, K., Almost complex submanifolds of a 6-dimensional sphere, Kodai Math. J. 6 (1983), 174–185.CrossRefGoogle Scholar
6.Spivak, M., A comprehensive introduction to differential geometry (Publish or Perish Inc., 1979).Google Scholar