Hostname: page-component-848d4c4894-v5vhk Total loading time: 0 Render date: 2024-06-30T14:00:15.443Z Has data issue: false hasContentIssue false
  • English
  • Français

Toeplitz operators and algebras of bounded analytic functions on the disk

Published online by Cambridge University Press:  18 May 2009

R. C. Smith
R. C. Smith
Affiliation:
Department of Mathematics and Statistics, Mississippi State University, Mississippi 39762, USA
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Here and throughout, A is a closed subalgebra of H∞ that contains the disk algebra and M(A) denotes the maximal ideal space of A. Because A contains the function fo(z) = z, we can define the fiber Mλ(A) of M(A) for λ ε ∂D (the unit circle) in the usual way; i.e., Mλ(A) = {φ ∈ M(A): fo(φ) = λ}. The Bergman space of the unit disk D is the L2(D, dx dy)-closure of A. Let 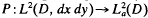be the orthogonal projection. For f ∈ L∞(D, dx dy), define the multiplication operator Mf: L2(D, dx dy)→ L2, (D, dx dy) by

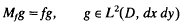
and define the Toeplitz operator 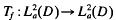by

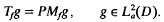
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 33 , Issue 2 , May 1991 , pp. 181 - 185
Copyright
Copyright © Glasgow Mathematical Journal Trust 1991

References

REFERENCES

1.Chang, S. Y. and Marshall, D., Some algebras of bounded analytic functions containing the disk algebra, in Banach spaces of analytic functions, Lecture Notes in Math. 604, Springer Verlag, 1977.Google Scholar
2.Coburn, L., Singular integral operators and Toeplitz operators on odd spheres, Indiana Univ. Math. J. 23, (1973), 433–439.CrossRefGoogle Scholar
3.Dawson, D., Subalgebras of H∞, Ph.D. Thesis, Indiana University, 1975.Google Scholar
4.Douglas, R., Banach algebra techniques in operator theory (Academic Press, 1972).Google Scholar
5.Gamelin, T., Uniform Algebras (Prentice-Hall, 1969).Google Scholar
6.Garnett, J., Bounded Analytic Functions (Academic Press, 1981).Google Scholar
7.Luecking, D., Inequalities on Bergman spaces, Illinois J. Math. 25 (1981), 1–11.CrossRefGoogle Scholar
8.McDonald, G. and Sundberg, C., Toeplitz operators on the disk, Indiana Univ. Math. J. 28 (1979), 595–611.CrossRefGoogle Scholar
9.Nehari, Z., Conformal Mapping (McGraw-Hill, 1952).Google Scholar
10.Smith, R., Toeplitz operators on abstract Hardy spaces, Glasgow Math. J. 30 (1988), 129–131.CrossRefGoogle Scholar
11.Sundberg, C., Exact sequences for generalized Toeplitz operators, Proc. Amer. Math. Soc. 101 (1987), 634–636.CrossRefGoogle Scholar