Hostname: page-component-77c89778f8-m8s7h Total loading time: 0 Render date: 2024-07-21T22:45:22.672Z Has data issue: false hasContentIssue false
  • English
  • Français

POSITIVE SOLUTIONS TO p(x)-LAPLACIAN–DIRICHLET PROBLEMS WITH SIGN-CHANGING NON-LINEARITIES

Published online by Cambridge University Press:  25 August 2010

XIANLING FAN
XIANLING FAN*
Affiliation:
Department of Mathematics, Lanzhou City University, Lanzhou 730070, PR China Department of Mathematics, Lanzhou University, Lanzhou 730000, PR China e-mail: fanxl@lzu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the p(x)-Laplacian–Dirichlet problem with sign-changing non-linearity of the form 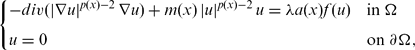where Ω ⊂ ℝN is a bounded domain, p ∈ C0(Ω) and infx∈Ωp(x) > 1, m ∈ L∞(Ω) is non-negative, f : ℝ → ℝ is continuous and f(0) > 0, the coefficient a ∈ L∞(Ω) is sign-changing in (Ω). We give some sufficient conditions to assure the existence of a positive solution to the problem for sufficiently small λ > 0. Our results extend the corresponding results established in the p-Laplacian case to the p(x)-Laplacian case.

Keywords

35J70
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 52 , Issue 3 , September 2010 , pp. 505 - 516
Copyright
Copyright © Glasgow Mathematical Journal Trust 2010

References

REFERENCES

1.Acerbi, E. and Mingione, G., Regularity results for a class of functionals with nonstandard growth, Arch. Ration. Mech. Anal. 156 (2001), 121–140.Google Scholar
2.Afrouzi, G. A. and Brown, K. J., Positive solutions for a semilinear elliptic problem with sign-changing nonlinearity, Nonlinear Anal. 36 (1999), 507–510.CrossRefGoogle Scholar
3.Alves, C. O. and Souto, M. A. S., Existence of solutions for a class of problems in ℝN involving the p(x)-Laplacian, Prog. Nonlinear Differ. Equ. Appl. 66 (2005), 17–32.Google Scholar
4.Antontsev, S. and Shmarev, S., Elliptic equations with anisotropic nonlinearity and nonstandard conditions, in Handbook of differential equations, stationary partial differential equations, vol. 3 (Chipot, M. and Quittner, P., Editors) (Elsevier B. V., North Holland, Amsterdam, 2006), 1–100.Google Scholar
5.Các, N. P., Fink, A. M. and Gatica, J. A., Nonnegative solutions to the radial Laplacian with nonlinearity that changes sign, Proc. Amer. Math. Soc. 123 (1995), 1393–1398.Google Scholar
6.Các, N. P., Gatica, J. A. and Li, Y., Positive solutions to semilinear problems with coefficient that changes sign, Nonlinear Anal. 37 (1999), 501–510.CrossRefGoogle Scholar
7.Diening, L., Hästö, P. and Nekvinda, A., Open problems in variable exponent Lebesgue and Sobolev spaces, in FSDONA04 proceedings (Drábek, P. and Rákosník, J. Editors), The Conference held in Milovy, May 28–June 2, 2004, (Math. Inst. Acad. Sci. Czech Republic, Praha, 2005), 38–58.Google Scholar
8.Dinu, T.-L., On a nonlinear eigenvalue problem in Sobolev spaces with variable exponent, Sib. Elektron. Mat. Izv. 2 (2005), 208–217.Google Scholar
9.Fan, X. L., Global C 1,α) regularity for variable exponent elliptic equations in divergence form, J. Differ. Equ. 235 (2007), 397–417.Google Scholar
10.Fan, X. L., On the sub-supersolution method for p(x)-Laplacian equations, J. Math. Anal. Appl. 330 (2007), 665–682.Google Scholar
11.Fan, X. L., Remarks on eigenvalue problems involving the p(x) -Laplacian, J. Math. Anal. Appl. 352 (2009), 85–98.Google Scholar
12.Fan, X. L. and Zhang, Q. H., Existence of solutions for p(x) -Laplacian Dirichlet problems, Nonlinear Anal. 52 (2003), 1843–1852.Google Scholar
13.Fan, X. L. and Zhao, D., A class of De Giorgi type and Hölder continuity, Nonlinear Anal. 36 (1999), 295–318.Google Scholar
14.Fan, X. L. and Zhao, D., On the spaces Lp(x)(Ω) and Wk,p(x)(Ω), J. Math. Anal. Appl. 263 (2001), 424–446.Google Scholar
15.Fan, X. L., Zhao, Y. Z., Zhang, Q. H., A strong maximum principle for p(x)-Laplace equations, Chin. Ann. Math. Ser. A 24 (2003) 495–500 (in Chinese), English translation: Chin. J. Contemp. Math. 24 (2003), 277–282.Google Scholar
16.Fu, Y. Q. and Zhang, X., A multiplicity result for p(x)-Laplacian problem in ℝN, Nonlinear Anal. 70 (2009), 2261–2269.Google Scholar
17.Hai, D. D., Positive solutions to a class of elliptic boundary value problems, J. Math. Anal. Appl. 227 (1998), 195–199.Google Scholar
18.Hai, D. D. and Xu, X., On a class of quasilinear problems with sign-changing nonlinearities, Nonlinear Anal. 64 (2006), 1977–1983.CrossRefGoogle Scholar
19.Harjulehto, P. and Hästö, P., An overview of variable exponent Lebesgue and Sobolev spaces, in Future Trends in Geometric Function Theory (Herron, D., Editor) (RNC Workshop, Jyväskylä, 2003), 85–93.Google Scholar
20.Harjulehto, P., Hästö, P., Lê, U. V. and Nuortio, M., Overview of differential equations with non-standard growth, Nonlinear Anal. 72 (2010), 4551–4574.Google Scholar
21.Jikov, V. V., Kozlov, S. M. and Oleinik, O. A., Homogenization of differential operators and integral functional (Springer-Verlag, Berlin, 1994). Translated from the Russian by G. A. Yosifan.Google Scholar
22.Kováčik, O. and Rákosnik, J., On spaces Lp(x) and Wk,p(x), Czech. Math. J. 41 (116) (1991), 592–618.Google Scholar
23.Marcellini, P., Regularity and existence of solutions of elliptic equations with (p, q)-growth conditions, J. Differ. Equ. 90 (1991), 1–30.CrossRefGoogle Scholar
24.Mihăilescu, M. and Rădulescu, V., A multiplicity result for a nonlinear degenerate problem arising in the theory of electrorheological fluids, Proc. R. Soc. Lond. Ser. A 462 (2006), 2625–2641.Google Scholar
25.Mihăilescu, M. and Rădulescu, V., On a nonhomogeneous quasilinear eigenvalue problem in Sobolev spaces with variable exponent, Proc. Amer. Math. Soc. 135 (2007), 2929–2937.CrossRefGoogle Scholar
26.Mihăilescu, M. and Rădulescu, V., Continuous spectrum for a class of nonhomogeneous differential operators, Manuscr. Math. 125 (2008), 157–167.Google Scholar
27.Růžička, M., Electrorheological fluids: Modeling and mathematical theory (Springer-Verlag, Berlin, 2000).CrossRefGoogle Scholar
28.Samko, S., On a progress in the theory of Lebesgue spaces with variable exponent: maximal and singular operators, Integral Transforms Spec. Funct. 16 (2005), 461–482.Google Scholar
29.Zhang, Q. H., Existence and asymptotic behavior of positive solutions for variable exponent elliptic systems, Nonlinear Anal. 70 (2009), 305–316.CrossRefGoogle Scholar
30.Zhikov, V. V., On some variational problems, Russ. J. Math. Phys. 5 (1997), 105–116.Google Scholar