Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-04-30T17:21:15.694Z Has data issue: false hasContentIssue false
  • English
  • Français

POSITIVE SOLUTIONS FOR A CLASS OF p(x)-LAPLACIAN PROBLEMS

Published online by Cambridge University Press:  01 September 2009

G. A. AFROUZI  and
H. GHORBANI
G. A. AFROUZI
Affiliation:
Department of Mathematics, Faculty of Basic Sciences, Mazandaran University, Babolsar, Iran e-mail: afrouzi@umz.ac.ir
H. GHORBANI
Affiliation:
Department of Mathematics, Faculty of Basic Sciences, Mazandaran University, Babolsar, Iran e-mail: afrouzi@umz.ac.ir
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the system 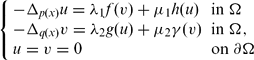where p(x), q(x) ∈ C1(RN) are radial symmetric functions such that sup|∇ p(x)| < ∞, sup|∇ q(x)| < ∞ and 1 < inf p(x) ≤ sup p(x) < ∞, 1 < inf q(x) ≤ sup q(x) < ∞, where −Δp(x)u = −div(|∇u|p(x)−2∇u), −Δq(x)v = −div(|∇v|q(x)−2∇v), respectively are called p(x)-Laplacian and q(x)-Laplacian, λ1, λ2, μ1 and μ2 are positive parameters and Ω = B(0, R) ⊂ RN is a bounded radial symmetric domain, where R is sufficiently large. We prove the existence of a positive solution when 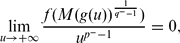for every M > 0, 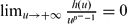and 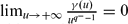. In particular, we do not assume any sign conditions on f(0), g(0), h(0) or γ(0).

Keywords

35J6035B3035B40
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 51 , Issue 3 , September 2009 , pp. 571 - 578
Copyright
Copyright © Glasgow Mathematical Journal Trust 2009

References

REFERENCES

1.Ali, J. and Shivaji, R., Positive solutions for a class of p-Laplacian systems with multiple parameters, J. Math. Anal. Appl. 335 (2007), 1013–1019.CrossRefGoogle Scholar
2.Chen, C. H., On positive weak solutions for a class of quasilinear elliptic systems, Nonlinear Anal. 62 (2005), 751–756.CrossRefGoogle Scholar
3.Fan, X. L., Wu, H. Q., and Waang, F. Z., Hartman-type results for p(t)-Laplacian systems, Nonlinear Anal. 52 (2003), 585–594.CrossRefGoogle Scholar
4.Fan, X. L. and Zhang, Q. H., Existence of solutions for p(x)-Laplacian Dirichlet problem, Nonlinear Anal. 52 (2003), 1843–1852.CrossRefGoogle Scholar
5.Fan, X. L., Zhang, Q. H. and Zhao, D.Eigenvalues of p(x)-Laplacian Dirichlet problem, J. Math. Anal. Appl. 302 (2005), 306–317.CrossRefGoogle Scholar
6.Fan, X. L. and Zhao, D., A class of De Giorgi type and Hölder continuity, Nonlinear Anal. TMA 36 (1999), 295–318.CrossRefGoogle Scholar
7.Fan, X. L. and Zhao, D., The quasi-minimizer of integral functionals with m(x) growth conditions, Nonlinear Anal. TMA 39 (2000), 807–816.CrossRefGoogle Scholar
8.Fan, X. L. and Zhao, D., On the spaces L p(x)(Ω) and W m,p(x) (Ω), J. Math. Anal. Appl. 263 (2001), 424–446.CrossRefGoogle Scholar
9.Hai, D. D. and Shivaji, R., An existence result on positive solutions for a class of p-Laplacian systems, Nonlinear Anal. 56 (2004), 1007–1010.CrossRefGoogle Scholar
10.Rûzicka, M., Electrorheological fluids: Modeling and mathematical theory, Lecture Notes in Math, vol. 1784 (Springer-Verlag, Berlin, 2000).CrossRefGoogle Scholar
11.Zhang, Q. H., Existence of positive solutions for a class of p(x)-Laplacian systems, J. Math. Anal. Appl. 302 (2005), 306–317.Google Scholar
12.Zhang, Q. H., Existence of positive solutions for elliptic systems with nonstandard p(x)-growth conditions via sub-supersolution method, Nonlinear Anal. 67 (2007), 1055–1067.CrossRefGoogle Scholar
13.Zhikov, V. V., Averaging of functionals of the calculus of variations and elasticity theory, Math. USSR Izv. 29 (1987), 33–36.CrossRefGoogle Scholar