Hostname: page-component-76fb5796d-zzh7m Total loading time: 0 Render date: 2024-04-28T19:09:26.079Z Has data issue: false hasContentIssue false
  • English
  • Français

ON WEAKLY RIGID RINGS

Published online by Cambridge University Press:  01 September 2009

A. R. NASR-ISFAHANI  and
A. MOUSSAVI
A. R. NASR-ISFAHANI
Affiliation:
Department of Mathematics, Tarbiat Modares University, PO Box 14115-175, Tehran, Iran e-mail: a_nasr_isfahani@yahoo.com, moussavi_a5@yahoo.com
A. MOUSSAVI
Affiliation:
Department of Mathematics, Tarbiat Modares University, PO Box 14115-175, Tehran, Iran e-mail: a_nasr_isfahani@yahoo.com, moussavi_a5@yahoo.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

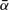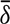Let R be a ring with a monomorphism α and an α-derivation δ. We introduce (α, δ)-weakly rigid rings which are a generalisation of α-rigid rings and investigate their properties. Every prime ring R is (α, δ)-weakly rigid for any automorphism α and α-derivation δ. It is proved that for any n, a ring R is (α, δ)-weakly rigid if and only if the n-by-n upper triangular matrix ring Tn(R) is (, )-weakly rigid if and only if Mn(R) is (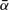, 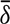)-weakly rigid. Moreover, various classes of (α, δ)-weakly rigid rings is constructed, and several known results are extended. We show that for an (α, δ)-weakly rigid ring R, and the extensions R[x], R[[x]], R[x; α, δ], R[x, x−1; α], R[[x; α]], R[[x, x−1; α]], the ring R is quasi-Baer if and only if the extension over R is quasi-Baer. It is also proved that for an (α, δ)-weakly rigid ring R, if any one of the rings R, R[x], R[x; α, δ] and R[x, x−1; α] is left principally quasi-Baer, then so are the other three. Examples to illustrate and delimit the theory are provided.

Keywords

16S3616W60
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 51 , Issue 3 , September 2009 , pp. 425 - 440
Copyright
Copyright © Glasgow Mathematical Journal Trust 2009

References

REFERENCES

1.Armendariz, E. P., A note on extensions of Baer and p.p.-rings, J. Austral. Math. Soc. 18 (1974), 470–473.CrossRefGoogle Scholar
2.Berberian, S. K., Baer *-rings, (Springer, Berlin, 1972).CrossRefGoogle Scholar
3.Birkenmeier, G. F., Baer rings and quasi-continuous rings have a MDSN, Pacific J. Math.. 97 (1981), 283–292.Google Scholar
4.Birkenmeier, G. F., Decompositions of Baer-like rings, Acta Math. Hungar.. 59 (1992), 319–326.CrossRefGoogle Scholar
5.Birkenmeier, G. F., Kim, J. Y. and Park, J. K., Polynomial extensions of Baer and quasi-Baer rings, J. Pure Appl. Algebra. 159 (2001), 24–42.CrossRefGoogle Scholar
6.Birkenmeier, G. F., Kim, J. Y. and Park, J. K., Principally quasi-Baer rings, Comm. Algebra. 29 (2) (2001), 639–660.CrossRefGoogle Scholar
7.Birkenmeier, G. F., Kim, J. Y. and Park, J. K., On polynomial extensions of principally quasi-Baer rings, Kyungpook Math. J.. 40 (2000), 247–253.Google Scholar
8.Birkenmeier, G. F., Park, J. K. and Rizvi, S. T., Ring hulls and applications, J. Algebra. 304 (2) (2006), 633–665.CrossRefGoogle Scholar
9.Clark, W. E., Twisted matrix units semigroup algebras, Duke Math. J.. 34 (1967), 417–424.Google Scholar
10.Faith, C., Injective quotient rings of commutative rings, in Module Theory, Lecture Notes in Mathematics 700, (Proc. Special Session, Amer. Math. Soc., Univ. Washington, Seattle, Wash., 1977) (Springer, Berlin), 151–203.Google Scholar
11.Han, J., Hirano, Y. and Kim, H., Semiprime ore extensions, Comm. Algebra. 28 (8) (2000) 3795–3801.CrossRefGoogle Scholar
12.Hashemi, E. and Moussavi, A., Polynomial extensions of quasi-Baer rings. Acta Math. Hungar.. 107 (3) (2005), 207–224.Google Scholar
13.Hirano, Y., On annihilator ideals of a polynomial ring over a noncommutative ring, J. Pure Appl. Algebra. 168 (2002), 45–52.Google Scholar
14.Hong, C. Y., Kim, N. K., Kwak, T., Ore extensions of Baer and p.p.-rings, J. Pure Appl. Algebra. 151 (2000), 215–226.CrossRefGoogle Scholar
15.Hong, C. Y., Kim, N. K., Kwak, T. and Rizvi, S. Tariq, Rigid ideals and radicals of Ore extensions, Algebra Colloq.. 12 (3) (2005), 399–412.Google Scholar
16.Jordan, D. A., Bijective extensions of injective ring endomorphisms, J. Lond. Math. Soc.. 25 (2) (1982), 435–448.CrossRefGoogle Scholar
17.Kaplansky, I., Rings of operators, (Benjamin, New York, 1965).Google Scholar
18.Krempa, J., Some examples of reduced rings, Algebra Colloq.. 3 (4) (1996) 289–300.Google Scholar
19.Lee, T. K. and Zhou, Y., Armendariz and reduced rings, Comm. Algebra. 32 (6) (2004), 2287–2299.CrossRefGoogle Scholar
20.Lee, Y. and Huh, C., Counterexamples on p.p.-rings, Kyungpook Math. J.. 38 (1998), 421–427.Google Scholar
21.Nasr-Isfahani, A. R. and Moussavi, A., Baer and quasi-Baer differential polynomial rings, Comm. Algebra. 36 (9) (2008), 3533–3542.CrossRefGoogle Scholar
22.Nasr-Isfahani, A. R. and Moussavi, A., Ore extensions of quasi-Baer rings, J. Algebra Appl. 7 (2) (2008), 211–224.CrossRefGoogle Scholar
23.Pollingher, P. and Zaks, A., On Baer and quasi-Baer rings, Duke Math. J.. 37 (1970), 127–138.Google Scholar
24.Zhou, Y., A simple proof of a theorem on quasi-Baer rings, Arch. Math.. 81 (2003), 253–254.CrossRefGoogle Scholar