Hostname: page-component-77c89778f8-vpsfw Total loading time: 0 Render date: 2024-07-17T04:12:46.907Z Has data issue: false hasContentIssue false
  • English
  • Français

On generating points of a lattice in the region

Published online by Cambridge University Press:  18 May 2009

D. M. E. Foster
D. M. E. Foster
Affiliation:
St. Salvator's College University of St. Andrews
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A lattice An in n-dimensional Euclidean space En consists of the aggregate of all points with coordinates (xx,…, xn), where

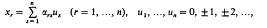
for some real ars (r, s = 1,…, n), subject to the condition ∥ αrs ∥nn ╪ 0. The determinant Δn of Λn, is denned by the relation 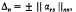, the sign being chosen to ensure that Δn > 0.

If A1…, An are the n points of Λn having coordinates (a11, a21…, anl),…, (a1n, a2n,…, ann), respectively, then every point of Λn may be expressed in the form

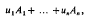
and Ai,…, An, together with the origin O, are said to generate Λn. This particular set of generating points is not unique; it may be proved that a necessary and sufficient condition that n points of Λn should generate the lattice is that the n × n determinant formed by their x coordinates should be ±Δn, or, equivalently, that the n×n determinant formed by their corresponding u-coordinates should be ±1.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 6 , Issue 3 , January 1964 , pp. 141 - 155
Copyright
Copyright © Glasgow Mathematical Journal Trust 1964

References

REFERENCES

1.Barnes, E. S., The minimum of the product of two values of a quadratic form, I, II and III, Proc. London Math. Soc. (3) 1 (1951), 257–283, 385–414, 415–434.CrossRefGoogle Scholar
2.Barnes, E. S., The non-negative values of quadratic forms, Proc. London Math. Soc. (3) 5 (1955), 185–196, Theorem 1.CrossRefGoogle Scholar
3.Chalk, J. H. H., A theorem of Minkowski on the product of two linear forms, Proc. Cambridge Phil. Soc. 49 (1953), 413–420.CrossRefGoogle Scholar
4.Chalk, J. H. H., On the product of n homogeneous linear forms, Proc. London Math. Soc. (3) 5 (1955), 449–473.CrossRefGoogle Scholar
5.Chalk, J. H. H., Integral bases for quadratic forms, Canad. J. Math. 15 (1963), 412–421.CrossRefGoogle Scholar
6.Chalk, J. H. H. and Rogers, C. A., On the product of three homogeneous linear forms, Proc. Cambridge Phil. Soc. 47 (1951), 251–259.CrossRefGoogle Scholar
7.Davenport, H., Non-homogeneous ternary quadratic forms, Ada Math. 80 (1948), 65–95; see also Barnes and Swinnerton-Dyer, Inhomogeneous minima of binary quadratic forms (I), AdaMath. 85 (1952), 259–323, especially §6.Google Scholar
8.Dickson, L. E., Introduction to the theory of numbers (Chicago, 1929).Google Scholar
9.Dickson, L. E., Studies in the theory of numbers (Chicago, 1930).Google Scholar
10.Korkine, A. and Zolotareff, G., Sur les formes quadratiques, Math. Ann. 6 (1873), 366–389; see also [9], Theorem 83.CrossRefGoogle Scholar
11.Macbeath, A. M., A new sequence of minima in the geometry of numbers, Proc. Cambridge Phil. Soc. 47 (1951), 266–273.CrossRefGoogle Scholar
12.Markoff, A., Sur les formes quadratiques binaires indéfinies, Math. Ann. 15 (1879), 381–406; see also Math. Ann. 56 (1903), 233–251; see also [8], Theorem 119.CrossRefGoogle Scholar
13.Minkowski, H., Ueber die Annäherung an eine reele Gröβie dursch rationale Zahlen, Math. Ann. 54 (1900), 91–124.CrossRefGoogle Scholar
14.Oppenheim, A., Values of quadratic forms, I, Quart. J. Math. Oxford Ser. (2) 4 (1953), 54–59, Theorem 1.CrossRefGoogle Scholar
15.Oppenheim, A., On indefinite binary quadratic forms, Ada Math. 91 (1954), 43–50.Google Scholar