Hostname: page-component-5c6d5d7d68-lvtdw Total loading time: 0 Render date: 2024-08-08T09:36:43.870Z Has data issue: false hasContentIssue false
  • English
  • Français

On a class of generalized functions

Published online by Cambridge University Press:  18 May 2009

K. Rowlands
K. Rowlands
Affiliation:
Department of Pure Mathematics, University College of Wales, Aberystwyth
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 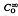be the complex linear space of all infinitely differentiable functions φ on the interval J = (a,b)(− ∞ ≦ a < 0 < b ≦ + ∞) such that φ(k)(0) = 0 for all non-negative integers k. Krabbe ([2], [3]) has defined a class of generalized functions on Jas an algebra ℳ of linear operators on 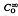and has developed an operational calculus for these operators. Shultz ([6], Theorem 2.18) has recently shown that ℳ is isomorphic to 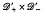, where 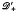(resp. 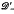) is the set of all distributions on J whose supports are contained in J+ = [0, b) (J- = (a,0]). In this paper we combine some of the ideas developed in [4] with results established in an earlier paper by Shultz to give an easier proof of the above result. Our methods also give a more direct proof of the main result (Theorem 1.22) of [2].

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 17 , Issue 1 , January 1976 , pp. 37 - 43
Copyright
Copyright © Glasgow Mathematical Journal Trust 1976

References

REFERENCES

1.Boehme, T. K., Continuity and perfect operators, J. London Math. Soc. 39 (1964), 355–358.Google Scholar
2.Krabbe, G., Linear operators and operational calculus, Part I, Studia Mathematica 40 (1971), 199–223.CrossRefGoogle Scholar
3.Krabbe, G., An algebra of generalized functions on an open interval: two-sided operational calculus, Pacific J. Math. 42 (1972), 381–411.Google Scholar
4.Rowlands, K., A convolution-integral representation for a class of linear operators, Proc. Cambridge Phil. Soc. 71 (1972), 51–60.Google Scholar
5.Shultz, H., Linear operators and operational calculus, Part II, Studia Mathematica 41 (1972), 1–25.CrossRefGoogle Scholar
6.Shultz, H., An algebra of distributions on an open interval, Trans. American Math. Soc. 169 (1972), 163–181.CrossRefGoogle Scholar
7.Titchmarsh, E. C., Theory of Fourier integrals (Oxford, 1937).Google Scholar
8.Weston, J. D., Positive perfect operators, Proc. London Math. Soc. (3) 10 (1960), 545–565.Google Scholar
9.Weston, J. D., An algebraic theory of generalized functions, Nieuw Archief voor Wiskunde (3) 18 (1970), 211–249.Google Scholar