Hostname: page-component-77c89778f8-vsgnj Total loading time: 0 Render date: 2024-07-19T11:55:21.095Z Has data issue: false hasContentIssue false
  • English
  • Français

Hilbert transforms and unitary equivalence

Published online by Cambridge University Press:  18 May 2009

R. Putnam
R. Putnam
Affiliation:
Purdue UniversityLafayette, Indiana
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If E is a subset of the real line of positive measure, then the associated Hilbert transform H = HE,

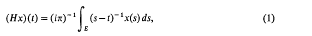
where the integral is a Cauchy principal value, is a bounded self-adjoint operator on L2(E) (cf. Muskhelishvili [4]). In case E = (-∞, ∞) the transformation is also unitary with a spectrum consisting of 1 and -1, each of infinite multiplicity (Titchmarsh [10]). If E is a inite interval the spectral representation of H has been given by Koppelman and Pincus [3]; see also Putnam [6]. In particular the spectrum of H is in this case the closed interval [-1, 1]. Moreover, according to Widom [11], the spectrum of H is [-1, 1] whenever E ≠ (-∞, ∞), that is, whenever

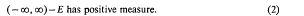
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 8 , Issue 2 , July 1967 , pp. 113 - 117
Copyright
Copyright © Glasgow Mathematical Journal Trust 1967

References

1.Hopf, E., Ergodentheorie, Chelsea (New York, 1948).Google Scholar
2.Kato, T., Perturbation of continuous spectra by trace class operators, Proc. Japan Acad. 33 (1957), 260–264.Google Scholar
3.Koppelman, W. and Pincus, J., Spectral representations for finite Hilbert transformations, Math. Zeit. 71 (1959), 399–407.CrossRefGoogle Scholar
4.Muskhelishvili, N. J., Singular integral equations (Groningen, 1953).Google Scholar
5.Putnam, C. R., On differences of unitarily equivalent self-adjoint operators, Proc. Glasgow Math. Assoc. 4 (1960), 103–107.CrossRefGoogle Scholar
6.Putnam, C. R., The spectra of generalized Hilbert transforms, /. Math. Mech. 14 (1965), 857–872.Google Scholar
7.Riesz, F. and Sz.-Nagy, B., Functional analysis, Ungar (New York, 1955).Google Scholar
8.Rosenblum, M., Perturbation of the continuous spectrum and unitary equivalence, Pacific J. Math. 7 (1957), 997–1010.CrossRefGoogle Scholar
9.Schatten, R., A theory of cross spaces, Ann. Math. Studies (Princeton, 1950).Google Scholar
10.Titchmarsh, E. C., Introduction to the theory of Fourier integrals (Oxford, 1948).Google Scholar
11.Widom, H., Singular integral equations in Lp, Trans. Amer. Math. Soc. 97 (1960), 131–160.Google Scholar