Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-26T01:05:33.006Z Has data issue: false hasContentIssue false
  • English
  • Français

GOLDIE*-SUPPLEMENTED MODULES

Published online by Cambridge University Press:  24 June 2010

G. F. BIRKENMEIER ,
F. TAKIL MUTLU ,
C. NEBİYEV ,
N. SOKMEZ  and
A. TERCAN
G. F. BIRKENMEIER
Affiliation:
Department of Mathematics, University of Louisiana at Lafayette, Lafayette, LA 70504 1010, USA e-mail: gfb1127@louisiana.edu
F. TAKIL MUTLU
Affiliation:
Department of Mathematics, Anadolu University, 26470 Eskisehir, Turkey e-mail: figent@anadolu.edu.tr
C. NEBİYEV
Affiliation:
Department of Mathematics, OnDokuz Mayıs University, 55139 Samsun, Turkey e-mail: cnebiyev@omu.edu.tr
N. SOKMEZ
Affiliation:
Department of Mathematics, OnDokuz Mayıs University, 55139 Samsun, Turkey e-mail: nozkan@omu.edu.tr
A. TERCAN
Affiliation:
Department of Mathematics, Hacettepe University, Beytepe Campus, 06532 Ankara, Turkey e-mail: tercan@hacettepe.edu.tr.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Motivated by a relation on submodules of a module used by both A. W. Goldie and P. F. Smith, we say submodules X, Y of M are β* equivalent, Xβ*Y, if and only if 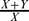is small in 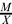and 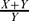is small in 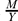. We show that the β* relation is an equivalence relation and has good behaviour with respect to addition of submodules, homomorphisms and supplements. We apply these results to introduce the class of 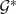-supplemented modules and to investigate this class and the class of H-supplemented modules. These classes are located among various well-known classes of modules related to the class of lifting modules. Moreover these classes are used to explore an open question of S. H. Mohamed and B. J. Mueller. Examples are provided to illustrate and delimit the theory.

Keywords

16D1016D50
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 52 , Issue A: Rings and Modules in Honour of Patrick F. Smith's 65th Birthday , July 2010 , pp. 41 - 52
Copyright
Copyright © Glasgow Mathematical Journal Trust 2010

References

REFERENCES

1.Akalan, E., Birkenmeier, G. F. and Tercan, A., Goldie Extending Modules, Commun. Algebra 37 (2), (2009), 663–683.CrossRefGoogle Scholar
2.Clark, J., Lomp, C., Vanaja, N. and Wisbauer, , Lifting modules: supplements and projectivity in module theory (Birkhäuser Verlag, Basel, Switzerland, 2006).Google Scholar
3.Fuchs, L., Infinite Abelian Groups (Academic Press, New York, 1970).Google Scholar
4.Goldie, A. W., Semi-prime rings with maximum condition, Proc. Lond. Math. Soc., 10 (1960), 201–220.CrossRefGoogle Scholar
5.Kosan, T. and Keskin, D., H-supplemented duo modules, J. Algebra Appl. 6, (2007), 965–971.CrossRefGoogle Scholar
6.Mohamed, S. H. and Muller, B. J., Continuous and discrete modules, London Mathematical Society Lecture Note Series, 147 (Cambridge University Press, Cambridge, 1990).CrossRefGoogle Scholar
7.Smith, P. F., Modules for which every submodule has a unique closure, in Ring theory Proceedings of the biennial Ohio state - Denison conference 1992 (Jain, S. K. and Rizvi, S. T., Editors) (World Scientific, Singapore, 1993), 302–313.Google Scholar
8.Wisbauer, R., Foundations of module and ring theory (Gordon and Breach, Philadelphia, 1991).Google Scholar