Article contents
GENERALIZED FINITE POLYLOGARITHMS
Published online by Cambridge University Press: 19 February 2020
Abstract
We introduce a generalization 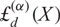 ${\rm{\pounds}}_d^{(\alpha)}(X)$
of the finite polylogarithms
${\rm{\pounds}}_d^{(\alpha)}(X)$
of the finite polylogarithms 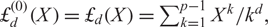 ${\rm{\pounds}}_d^{(0)}(X) = {{\rm{\pounds}}_d}(X) = \sum\nolimits_{k = 1}^{p - 1} {X^k}/{k^d}$
, in characteristic p, which depends on a parameter α. The special case
${\rm{\pounds}}_d^{(0)}(X) = {{\rm{\pounds}}_d}(X) = \sum\nolimits_{k = 1}^{p - 1} {X^k}/{k^d}$
, in characteristic p, which depends on a parameter α. The special case 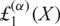 ${\rm{\pounds}}_1^{(\alpha)}(X)$
was previously investigated by the authors as the inverse, in an appropriate sense, of a parametrized generalization of the truncated exponential which is instrumental in a grading switching technique for nonassociative algebras. Here, we extend such generalization to
${\rm{\pounds}}_1^{(\alpha)}(X)$
was previously investigated by the authors as the inverse, in an appropriate sense, of a parametrized generalization of the truncated exponential which is instrumental in a grading switching technique for nonassociative algebras. Here, we extend such generalization to 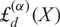 ${\rm{\pounds}}_d^{(\alpha)}(X)$
in a natural manner and study some properties satisfied by those polynomials. In particular, we find how the polynomials
${\rm{\pounds}}_d^{(\alpha)}(X)$
in a natural manner and study some properties satisfied by those polynomials. In particular, we find how the polynomials 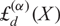 ${\rm{\pounds}}_d^{(\alpha)}(X)$
are related to the powers of
${\rm{\pounds}}_d^{(\alpha)}(X)$
are related to the powers of 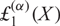 ${\rm{\pounds}}_1^{(\alpha)}(X)$
and derive some consequences.
${\rm{\pounds}}_1^{(\alpha)}(X)$
and derive some consequences.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2020. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust
References
REFERENCES
- 1
- Cited by




