Article contents
Factorization of Matrices and Minkowski's Conjecture
Published online by Cambridge University Press: 18 May 2009
Extract
Let Rn denote real Euclidean space of n dimensions. If
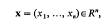
define 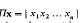 , and (as usual)
, and (as usual) 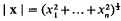 so that, by the inequality of arithmetic and geometric means,
so that, by the inequality of arithmetic and geometric means,

Let Λ0 be the integer lattice, consisting of those points in Rn whose co-ordinates are integers. A non-singular n × n matrix M will be called a Minkowski matrix, if, for any point a ∈ Rn, there exists a point x ∈ Λ0 such that

It was shown by Minkowski that, when n = 2, every non-singular matrix is a Minkowski matrix, and that, for general n, every rational non-singular matrix is a Minkowski matrix. Minkowski is also said to have conjectured that every non-singular matrix is a Minkowski matrix, whatever the value of n. For n = 3, this was proved by Remak [5], and a much simpler proof was given later by Davenport [2]. For n = 4, it was proved by Dyson [3], who used a method similar to that of Remak and Davenport, but required the methods of algebraic topology to deal with some of the complications which arise in the higher dimension. Since this method depends also on the reduction of quadratic forms, it is quite likely that it might fail for higher values of n even if the topological difficulties could be overcome. Therefore, an alternative proof for n = 3, due to Birch and Swinnerton-Dyer [1], is of some interest, though in this dimension it is more complicated than Davenport's proof. A good deal of their analysis applies to general n, and they showed that for all n there is a neighbourhood of the unit matrix I that consists entirely of Minkowski matrices.
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1961
References
- 10
- Cited by




