Hostname: page-component-76fb5796d-skm99 Total loading time: 0 Render date: 2024-04-26T04:46:36.463Z Has data issue: false hasContentIssue false
  • English
  • Français

EXTREME POINT METHODS IN THE STUDY OF ISOMETRIES ON CERTAIN NONCOMMUTATIVE SPACES

Part of: Selfadjoint operator algebras Special classes of linear operators

Published online by Cambridge University Press:  06 August 2021

PIERRE DE JAGER  and
JURIE CONRADIE
PIERRE DE JAGER
Affiliation:
Department of Mathematical Sciences, University of South Africa, P.O. Box, 392, Pretoria 0003, South Africa e-mail: dejagp@unisa.ac.za
JURIE CONRADIE
Affiliation:
Department of Mathematics and Applied Mathematics, University of Cape Town, Cape Town, South Africa e-mail: jurie.conradie@uct.ac.za
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we characterize surjective isometries on certain classes of noncommutative spaces associated with semi-finite von Neumann algebras: the Lorentz 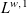spaces $L^{w,1}$ , as well as the spaces 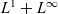$L^1+L^\infty$ and 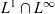$L^1\cap L^\infty$ . The technique used in all three cases relies on characterizations of the extreme points of the unit balls of these spaces. Of particular interest is that the representations of isometries obtained in this paper are global representations.

MSC classification

Primary: 47B38: Operators on function spaces (general)
Secondary: 46L52: Noncommutative function spaces
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 64 , Issue 2 , May 2022 , pp. 462 - 483
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bennett, C. and Sharpley, R., Interpolation of operators (Academic Press, 1988).Google Scholar
Bikchentaev, A., Block projection operator on normed solid spaces of measurable operators (Russian), Izv. Vyssh. Uchebn. Zaved. Mat. 2 (2012), 86–91 [English translation in Russian Math. (Iz. VUZ) 56(2) (2012), 75–79].CrossRefGoogle Scholar
Blackadar, B., Operator algebras: Theory of $C^*$ -algebras and von Neumann algebras, Encyclopedia of Mathematical Sciences, vol. 122, Operator Algebras and Non-Commutative Geometry III (Springer-Verlag, 2006).CrossRefGoogle Scholar
Carothers, N. L., Dilworth, S. J. and Trautman, D. A., On the geometry of the unit spheres of the Lorentz spaces $L^{w,1}$ , Glasgow Math. J. 34 (1992), 21–25.CrossRefGoogle Scholar
Carothers, N. L., Haydon, R. and Lin, P., On the isometries of the Lorentz function spaces, Israel J. Math. 84 (1993), 265–287.CrossRefGoogle Scholar
Chilin, V. I., Medzhitov, A. M. and Sukochev, F. A., Isometries of non-commutative Lorentz spaces, Math. Z. 200 (1989), 527–545.CrossRefGoogle Scholar
Chilin, V. I., Krygin, A. V and Sukochev, F. A., Extreme points of convex fully symmetric sets of measurable operators, Integr. Equat. Oper. Th. 15(2) (1992), 186–226.CrossRefGoogle Scholar
Choda, H., An extremal property of the polar decomposition in von Neumann algebras, Proc. Japan Acad., 46 (1970), 341–344.CrossRefGoogle Scholar
Conway, J. B., A course in functional analysis, 2nd edition (Springer 2007).CrossRefGoogle Scholar
CzerwiŃska, M. M., KamiŃska, A. and Kubiak, D., Smooth and strongly smooth points in symmetric spaces of measurable operators, Positivity, 16 (2012), 29–51.CrossRefGoogle Scholar
de Jager, P., Isometries on symmetric spaces associated with semi-finite von Neumann algebras, Ph.D. Thesis, University of Cape Town, 2017 (Available online at https://open.uct.ac.za/handle/11427/25167)Google Scholar
de Jager, P. and Conradie, J. J., Extension of projection mappings, Quaest. Math. 43 (2020), 1047–1064.CrossRefGoogle Scholar
de Jager, P. and Conradie, J. J., Isometries between non-commutative symmetric spaces associated with semi-finite von Neumann algebras, Positivity 24 (2020), 815–835.CrossRefGoogle Scholar
de Pagter, B., Non-commutative Banach function spaces, Positivity: Trends Math. (BirkhÄuser, Basel, 2007), 197–227.CrossRefGoogle Scholar
Dodds, P. G., Dodds, T. K.-Y. and de Pagter, B., Non-commutative KÖthe duality, Trans. Amer. Math. Soc. 339 (1993), 717–750.Google Scholar
Dodds, P. G., Dodds, T. K.-Y. and de Pagter, B., Normed KÖthe spaces: A non-commutative viewpoint, Indag. Math. 25 (2014), 206–249.CrossRefGoogle Scholar
Fack, T. and Kosaki, H., Generalized s-numbers of $\tau$ -measurable operators, Pacific J. Math. 123 (1986), 269–300.CrossRefGoogle Scholar
Fleming, R. J. and Jamison, J. E., Isometries on Banach spaces: Vector-valued function spaces, vol. 2 (Chapman and Hall/CRC, 2008).Google Scholar
Foralewski, P., Hudzik, H., and PŁuciennik, R., Orlicz spaces without extreme points, J. Math. Anal. Appl. 361 (2010), 506–519.CrossRefGoogle Scholar
Foralewski, P., Some remarks on the geometry of Lorentz spaces $\Lambda_{1,w}$ , Indag. Math. 23 (2012), 361–376.CrossRefGoogle Scholar
GrzaŚlewicz, R., Hudzik, H. and Kurc, W., Extreme and exposed points in Orlicz spaces, Can. J. Math. 44(3) (1992), 505–515.CrossRefGoogle Scholar
GrzaŚlewicz, R. and Schaefer, H. H., Surjective isometries of $L^1\cap L^\infty[0,\infty)$ and $L^1+L^\infty[0,\infty)$ , Indag. Math. (N.S.) 3(2) (1992), 173–178.Google Scholar
Huang, J., Sukochev, F. and Zanin, D., Logarithmic submajorisation and order-preserving linear isometries, J. Funct. Anal., 278(4) (2020).CrossRefGoogle Scholar
Huang, J. and Sukochev, F., Hermitian operators and isometries on symmetric operator spaces, 2021, preprint, arXiv:2101.03667v1.Google Scholar
Hudzik, H. and WisŁa, M., On extreme points of Orlicz spaces with Orlicz norm, Collect. Math. 44 (1993), 135–146.Google Scholar
Kadison, R. V., Isometries of operator algebras, Ann. Math., 54(2) (1951), 325–338.CrossRefGoogle Scholar
Kadison, R. V and Ringrose, J. R., Fundamentals of the theory of operator algebras, vol. 1, Second printing (BirkhÄuser, Academic Press, 1997).Google Scholar
Kadison, R. V and Ringrose, J. R., Fundamentals of the theory of operator algebras, vol. 2, Second printing, (BirkhÄuser, Academic Press, 1997).Google Scholar
Kalton, N. J. and Sukochev, F. A., Symmetric norms and spaces of operators, J. Reine Angew. Math., 621 (2008), 81–121.Google Scholar
Labuschagne, L. E. and Majewski, W. A., Maps on noncommutative Orlicz spaces, Illinois J. Math. 55(3) (2011), 1053–1081.CrossRefGoogle Scholar
Schaefer, H. H., On convex hulls, Arch. Math. 58 (1992), 160–163.CrossRefGoogle Scholar
Terp, M., $L^p$ -spaces associated with von Neumann algebras, Rapport No. 3a, (University of Copenhagen, 1981).Google Scholar
Weigt, M., Jordan homomorphisms between algebras of measurable operators, Quaest. Math., 32 (2009), 203–214.CrossRefGoogle Scholar
Yeadon, F. J., Isometries of non-commutative $L^p$ -spaces, Math. Proc. Camb. Phil. Soc., 90 (1981), 41–50.CrossRefGoogle Scholar