Hostname: page-component-77c89778f8-m42fx Total loading time: 0 Render date: 2024-07-17T16:49:42.769Z Has data issue: false hasContentIssue false
  • English
  • Français

EXAMPLE OF A GROUP WHOSE QUANTUM ISOMETRY GROUP DOES NOT DEPEND ON THE GENERATING SET

Published online by Cambridge University Press:  28 January 2018

ARNAB MANDAL
ARNAB MANDAL*
Affiliation:
School of Mathematical Sciences, National Institute of Science Education and Research Bhubaneswar, HBNI, Jatni 752050, India e-mail: arnabmaths@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we have shown that the quantum isometry group of Cr*(ℤ), denoted by ℚ(ℤ, S) as in Goswami and Mandal, Rev. Math. Phys.29(3) (2017), 1750008, with respect to a symmetric generating set S does not depend on the generating set S. Moreover, we have proved that the result is no longer true if the group ℤ is replaced by 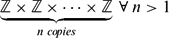$\underbrace{\mathbb{Z} \times \mathbb{Z} \times\cdots \times \mathbb{Z}}_{n \ copies} \ \forall \ n>1$.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 61 , Issue 1 , January 2019 , pp. 1 - 11
Copyright
Copyright © Glasgow Mathematical Journal Trust 2018 

References

REFERENCES

1. Banica, T., Quantum automorphism groups of small metric spaces, Pacific J. Math. 219 (1) (2005), 27–51.Google Scholar
2. Banica, T., Quantum automorphism groups of homogeneous graphs, J. Funct. Anal. 224 (2) (2005), 243–280.Google Scholar
3. Banica, T. and Skalski, A., Quantum symmetry groups of C*-algebras equipped with orthogonal filtrations, Proceedings of the LMS 106 (5) (2013), 980–1004.Google Scholar
4. Banica, T. and Skalski, A., Two parameter families of quantum symmetry groups, J. Funct. Anal}. 260 (2011), 3252–3282.Google Scholar
5. Banica, T. and Skalski, A., Quantum isometry groups of duals of free powers of cyclic groups, Int. Math. Res. Not. 9 (2012), 2094–2122.Google Scholar
6. Bhowmick, J. and Goswami, D., Quantum isometry groups: Examples and computations, Comm. Math. Phys}. 285 (2009), 421–444.Google Scholar
7. Bhowmick, J. and Goswami, D., Quantum group of orientation preserving Riemannian isometries, J. Funct. Anal}. 257 (2009), 2530–2572.Google Scholar
8. Bhowmick, J. and Skalski, A., Quantum isometry groups of noncommutative manifolds associated to group C*-algebras, J. Geom. Phys. 60 (10) (2010), 1474–1489.Google Scholar
9. Bichon, J., Quantum automorphism groups of finite graphs, Proceedings of the American Mathematical Society 131 (2003), 665–673.Google Scholar
10. Chari, V. and Pressley, A., A guide to quantum groups (Cambridge University Press, Cambridge, UK, 1994).Google Scholar
11. Connes, A., Compact metric spaces, Fredholm modules and hyperfiniteness, Ergodic Theory Dyn. Syst. 9 (2) (1989), 207–220.Google Scholar
12. Connes, A., Noncommutative geometry (Academic Press, London-New York, 1994).Google Scholar
13. Dalecki-Liszka, J. and Soltan, P. M., Quantum isometry groups of symmetric groups, Int. J. Math. 23 (7) (2012), 1250074, 25 p.Google Scholar
14. Drinfeld, V. G., Quantum groups, Proceedings of the International Congress of Mathematicians (Berkeley, 1986).Google Scholar
15. Goswami, D., Quantum group of isometries in classical and non commutative geometry, Comm. Math. Phys. 285 (1) (2009), 141–160.Google Scholar
16. Goswami, D. and Mandal, A., Quantum isometry groups of dual of finitely generated discrete groups and quantum groups, Rev. Math. Phys. 29 (3) (2017), 1750008, 38 p.Google Scholar
17. Mandal, A., Quantum isometry group of dual of finitely generated discrete groups-II, Ann. Math. Blaise Pascal. 23 (2) (2016), 219–247.Google Scholar
18. Manin, Y., Quantum groups and non-commutative geometry, Publ. CRM, 1561 (Univ. de Montreal, 1988).Google Scholar
19. Maes, A. and Van Daele, A., Notes on compact quantum groups, Nieuw Arch. Wisk. (4) 16 (1–2) (1998), 73–112.Google Scholar
20. Ozawa, N. and Rieffel, M. A., Hyperbolic group C*-algebras and free product C*-algebras as compact quantum metric spaces, Canad. J. Math. 57 (5) (2005), 1056–1074.Google Scholar
21. Skalski, A. and Soltan, P. M., Projective limits of quantum symmetry groups and doubling construction of Hopf algebra, Infin. Dimens. Anal. Quantum Probab. Relat. Top. 17 (2014), 1450012-1–1450012-27.Google Scholar
22. Tao, J. and Qiu, D., Quantum isometry groups for dihedral group D 2(2n+1), J. Geom. Phys. 62 (9) (2012), 1977–1983.Google Scholar
23. Wang, S., Quantum symmetry groups of finite spaces, Comm. Math. Phys. 195 (1998), 195–211.Google Scholar
24. Wornowicz, L. S., Compact matrix pseudogroups, Comm. Math. Phys. 111 (1987), 613–665.Google Scholar