Hostname: page-component-848d4c4894-r5zm4 Total loading time: 0 Render date: 2024-06-23T12:28:57.164Z Has data issue: false hasContentIssue false
  • English
  • Français

THE DIVISIBILITY OF THE CLASS NUMBER OF THE IMAGINARY QUADRATIC FIELD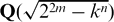

Published online by Cambridge University Press:  09 December 2011

ZHU MINHUI  and
WANG TINGTING
ZHU MINHUI
Affiliation:
School of Science, Xi'an Polytechnic University, Xi'an, Shaanxi, P.R. China e-mail: xiao-zhu123@sohu.com
WANG TINGTING
Affiliation:
Department of Mathematics, Northwest University, Xi'an, Shaanxi, P.R. China e-mail: tingtingwang126@126.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let hK denote the class number of the imaginary quadratic field 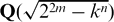, where m and n are positive integers, k is an odd integer with k > 1 and 22m < kn. In this paper we prove that if either 3 ∣ n and 22m − kn ≡ 5(mod 8) or n = 3 and k = (22m+2 −1)/3, then ∣ hK. Otherwise, we have n ∣ hK.

Keywords

11R1111R29
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 54 , Issue 1 , January 2012 , pp. 149 - 154
Copyright
Copyright © Glasgow Mathematical Journal Trust 2011

References

REFERENCES

1.Ankeny, N. C. and Chowla, S., On the divisibility of the class number of quadratic fields, Pacific J. Math. 5 (4) (1955), 321–324.CrossRefGoogle Scholar
2.Bilu, Y., Hanrot, G. and Voutier, P. M. (with an appendix by M. Mignotte), Existence of primitive divisors of Lucas and Lehmer numbers, J. Reine Angew. Math. 539 (2001), 75–122.Google Scholar
3.Cowles, M. J., On the divisibility of the class number of imaginary quadratic fields, J. Number Theory 12 (2) (1980), 113–115.CrossRefGoogle Scholar
4.Gross, B. H. and Rohrlich, D. E., Some results on the Mordell–Weil group of the Jacobian of the Fermat curve, Invent. Math. 44 (2) (1978), 201–224.CrossRefGoogle Scholar
5.Heuberger, C. and Le, M. H., On the generalized Ramanujan–Nagell equation x 2 + D = pZ, J. Number Theory 78 (4) (1999), 312–331.CrossRefGoogle Scholar
6.Hua, L. K., Introduction to number theory (Springer-Verlag, Berlin, 1982).Google Scholar
7.Kishi, Y., Note on the divisibility of the class number of certain imaginary quadratic fields, Glasgow Math. J. 51 (1) (2009), 187–191 (Corrigendum: Glasgow Math. J. 52 (2) (2010), 207–208).CrossRefGoogle Scholar
8.Mollin, R. A., Diophantine equations and class numbers, J. Number Theory 24 (1) (1986), 7–19.CrossRefGoogle Scholar
9.Mollin, R. A., Solutions, of diophantine equations and divisibility of class numbers of complex quadratic fields, Glasgow Math. J. 38 (2) (1996), 195–197.CrossRefGoogle Scholar
10.Voutier, P. M., Primitive divisors of Lucas and Lehmer sequences, Math. Comp. 64 (5) (1995), 869–888.CrossRefGoogle Scholar