Hostname: page-component-848d4c4894-mwx4w Total loading time: 0 Render date: 2024-06-19T09:20:25.548Z Has data issue: false hasContentIssue false
  • English
  • Français

Discrete free products of two complex cyclic matrix groups

Published online by Cambridge University Press:  18 May 2009

Ronald J. Evans
Ronald J. Evans
Affiliation:
Mathematics Department, University of California, San Diego La Jolla, California 92093
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

All 2-by-2 matrices in this paper are to be viewed as linear fractional transformations on the extended complex plane ℂ*. Let L+ and L− be the open half-planes to the right and left, respectively, of the extended imaginary axis L. Let Λ be the set of complex 2-by-2 matrices A with real trace and determinant ±1 such that A(L+) ⊂L−. Let Ω = Ω1 ∪ Ω2 ∪ Ω3 ∪ Ω4, Where

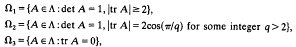
and

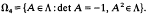
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 20 , Issue 1 , January 1979 , pp. 69 - 80
Copyright
Copyright © Glasgow Mathematical Journal Trust 1979

References

REFERENCES

1.Evans, R. J., A fundamental region for Hecke's modular group, J. Number Theory 5 (1973), 108–115.CrossRefGoogle Scholar
2.Evans, R. J., Free products of two real cyclic matrix groups, Glasgow Math. J. 15 (1974), 121–128.CrossRefGoogle Scholar
3.Lehner, J., Discontinuous groups and automorphic functions, Math. Surveys of the Amer. Math. Soc. 8 (Providence, R.I., 1964).CrossRefGoogle Scholar
4.Newman, M., Integral matrices (Academic Press, 1972).Google Scholar
5.Purzitsky, N., Two-generator discrete free products, Math. Z.. 126 (1972), 209–223.CrossRefGoogle Scholar
6.Purzitsky, N., All two-generator Fuchsian groups, Math. Z.. 147 (1976), 87–92.CrossRefGoogle Scholar