Hostname: page-component-848d4c4894-nmvwc Total loading time: 0 Render date: 2024-06-25T11:28:29.020Z Has data issue: false hasContentIssue false
  • English
  • Français

Clifford division algebras and anisotropic quadratic forms: two counterexamples

Published online by Cambridge University Press:  18 May 2009

P. Mammone  and
J. P. Tignol
P. Mammone
Affiliation:
Université de Mons-Hainaut, B-7000 Mons Université Catholique de Louvain, B-1348 Louvain-La-Neuve
J. P. Tignol
Affiliation:
Université de Mons-Hainaut, B-7000 Mons Université Catholique de Louvain, B-1348 Louvain-La-Neuve
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a recent paper [3], D. W. Lewis proposed the following conjecture. (The notation is the same as that in [2] and [3].)

Conjecture. Let F be a field of characteristic not 2 and let a1, b1…, an, bn ∈ Fx. The tensor product of quaternion algebras

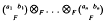
is a division algebra if and only if the quadratic form over F

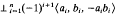
is anisotropic.

This equivalence indeed holds for n = 1 as is well known [2, Theorem 2.7], and Albert [1] (see also [4, §15.7]) has shown that it also holds for n = 2. The aim of this note is to provide counterexamples to both of the implications for n ≥ 3.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 28 , Issue 2 , July 1986 , pp. 227 - 228
Copyright
Copyright © Glasgow Mathematical Journal Trust 1986

References

REFERENCES

1.Albert, A. A., A construction of non-cyclic normal division algebras, Bull. Amer. Math. Soc. 38 (1932), 449–456.CrossRefGoogle Scholar
2.Lam, T.-Y., The algebraic theory of quadratic forms (Benjamin, 1973).Google Scholar
3.Lewis, D. W., A note on Clifford algebras and central division algebras with involution, Glasgow Math. J. 26 (1985), 171–176.CrossRefGoogle Scholar
4.Pierce, R. S., Associative algebras (Springer, 1982).CrossRefGoogle Scholar
5.Tignol, J. P., Algèbres indècomposables d'exposant premier, to appear in Adv. in Maths.Google Scholar