Hostname: page-component-77c89778f8-m42fx Total loading time: 0 Render date: 2024-07-17T16:04:36.886Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterisations of partially continuous, strictly cosingular and φ- type operators

Published online by Cambridge University Press:  18 May 2009

L. E. Labuschagne
L. E. Labuschagne
Affiliation:
Department of Mathematics, University of Stellenbosch, Stellenbosch 7600, South Africa
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We will denote the dimension of a subspace M of X by dim M and the codimension of M with respect to X by codxM or simply cod M if there is no danger of confusion. The classes of infinite dimensional and closed infinite codimensional subspaces of X will be denoted by 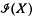and 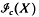respectively with ℱ(X) and ℱ(X) denoting the classes of finite dimensional and of finite codimensional subspaces of X respectively. For a subspace M of X we denote the injection of M into X by 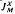and the quotient map from X onto the quotient space X/M by 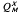. Where there is no danger of confusion we will write JM and QM. The injection of X into its completion 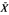will be denoted by Jx. Letting X′ denote the continuous dual of X we remark that since X′ is isometric to (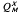)′, these two spaces will be considered identical where convenient. The orthogonal complements of subsets M ⊂ X in X′ and K ⊂ X′ in X will be denoted by M⊥ and ⊥K respectively; M⊥X and X⊥K will be used if there is danger of confusion.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 33 , Issue 2 , May 1991 , pp. 203 - 212
Copyright
Copyright © Glasgow Mathematical Journal Trust 1991

References

REFERENCES

1.Cross, R. W., Linear transformations of Tauberian type in normed spaces, Note Mat., to appear.Google Scholar
2.Cross, R. W., Properties of some norm related functions of unbounded linear operators, Math. Z. 199 (1988), 285–302.CrossRefGoogle Scholar
3.Cross, R. W., Some continuity properties of linear transformations in normed spaces, Glasgow Math. J. 30 (1988), 243–247.CrossRefGoogle Scholar
4.Cross, R. W., Unbounded linear transformations of upper semi-Fredholm type in normed spaces, Portugal. Math. 47 (1990), 61–79.Google Scholar
5.Cross, R. W. and Labuschagne, L. E., Characterisations of operators of lower semi-Fredholm type in normed spaces, Preprint, Dept. of Mathematics, Univ. of Cape Town.Google Scholar
6.Cross, R. W. and Labuschagne, L. E., Partially continuous and semi-continuous linear operators in normed spaces, Expo. Math. 7 (1989), 189–191.Google Scholar
7.Goldberg, S., Unbounded linear operators (McGraw-Hill, 1966).Google Scholar
8.Jarchow, H., Locally convex spaces (BG Teubner, Stuttgart, 1981).CrossRefGoogle Scholar
9.Köthe, G., General linear transformations of locally convex spaces, Math. Ann. 159 (1965), 309–328.CrossRefGoogle Scholar
10.Labuschagne, L. E., Unbounded strictly cosingular operators and their adjoints, Preprint, Dept. of Mathematics, Univ. of Stellenbosch.Google Scholar
11.Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces I (Springer-Verlag, 1977).CrossRefGoogle Scholar
12.Mackey, G., Note on a theorèm of Murray, Bull. Amer. Math. Soc. 52 (1946), 322–325.CrossRefGoogle Scholar
13.Pelczynski, A., On strictly singular and strictly cosingular operators I, II, Bull. Acad. Polon. Sci. Sér. Sci. Math. Astr. Phys. 13 (1965), 31–41.Google Scholar
14.Robertson, A. P. and Robertson, W. J., Topological vector spaces (2nd ed.) (Cambridge University Press, 1973).Google Scholar
15.Whitley, R. J., Strictly singular operators and their conjugates, Trans. Amer. Math. Soc. 113 (1964), 252–261.CrossRefGoogle Scholar