Hostname: page-component-848d4c4894-xm8r8 Total loading time: 0 Render date: 2024-07-02T22:14:43.505Z Has data issue: false hasContentIssue false
  • English
  • Français

Averaging operators in non commutative Lp spaces I

Published online by Cambridge University Press:  18 May 2009

Christopher Barnett
Christopher Barnett
Affiliation:
Bedford College London, NW1 4N6
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The origin of the theory of averaging operators is explained in [1]. The theory has been developed on spaces of continuous functions that vanish at infinity by Kelley in [3] and on the Lp spaces of measure theory by Rota [5]. The motivation for this paper arose out of the latter paper. The aim of this paper is to prove a generalisation of Rota's main representation theorem (every average is a conditional expectation) in the context of a ‘non commutative integration’. This context is as follows. Let 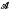be a finite von Neumann algebra and ϕ a faithful normal finite trace on 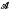such that ϕ(I) = 1, where I is the identity of 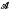. We can construct the Banach spaces Lp (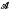, ϕ), where 1 ≤ p < °, with norm ∥x∥p = ϕ(÷x÷p)1/p, of possibly unbounded operators affiliated with 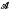, as in [9]. We note that 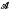is dense in Lp(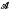, ϕ). These spaces share many of the features of the Lp spaces of measure theory; indeed if 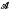is abelian then Lp(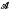,ϕ) is isometrically isomorphic to Lp of some measure space.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 24 , Issue 1 , January 1983 , pp. 71 - 74
Copyright
Copyright © Glasgow Mathematical Journal Trust 1983

References

REFERENCES

1.Birkhoff, G., Averaging operators in Symposium in lattice theory (AMS 1960).Google Scholar
2.Dunford, N. and Schwartz, J. T., Linear operators, Part 1 (Interscience, 1958).Google Scholar
3.Kelley, J. L., Averaging operators in C∞(X), Illinois J. Math. 2 (1958), 214–223.CrossRefGoogle Scholar
4.Loomis, L. H., Abstract harmonic analysis (Van Nostrand, 1953).Google Scholar
5.Rota, G. C., On the representation of averaging operators, Rend. Sem. Mat. Univ. Padova 30 (1960), 52–64.Google Scholar
6.Segal, I. E., A non commutative extension of abstract integration, Ann. of Math. 57 (1953), 401–457.CrossRefGoogle Scholar
7.Takesaki, M., Theory of operator algebras I, (Springer-Verlag, 1979).CrossRefGoogle Scholar
8.Umegaki, H., Conditional expectation in an operator algebra II, Tohoku Math. J., 8 (1956), 86–100.CrossRefGoogle Scholar
9.Yeadon, F. J., Non commutative L p spaces, Math. Proc. Cambridge Philos. Socll (1975), 91–102.CrossRefGoogle Scholar
10.Yeadon, F. J., Ergodic theorems for semifinite von Neumann algebras I, J. London. Math. Soc. (2), 16 (1977), 326–332.CrossRefGoogle Scholar