No CrossRef data available.
Article contents
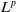 $L^p$ harmonic 1-forms on hypersurfaces with finite index
$L^p$ harmonic 1-forms on hypersurfaces with finite index
Published online by Cambridge University Press: 02 November 2022
Abstract
In the present note, we establish a finiteness theorem for 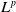 $L^p$ harmonic 1-forms on hypersurfaces with finite index, which is an extension of the result of Choi and Seo (J. Geom. Phys. 129 (2018), 125–132).
$L^p$ harmonic 1-forms on hypersurfaces with finite index, which is an extension of the result of Choi and Seo (J. Geom. Phys. 129 (2018), 125–132).
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust





