Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
Hostname: page-component-7f7b94f6bd-98q29 Total loading time: 0.21 Render date: 2022-06-30T23:01:16.909Z Has data issue: true Feature Flags: { "shouldUseShareProductTool": true, "shouldUseHypothesis": true, "isUnsiloEnabled": true, "useRatesEcommerce": false, "useNewApi": true } hasContentIssue true
  • English
Glasgow Mathematical Journal Glasgow Mathematical Journal

Article contents

Homotopy commutativity in Hermitian symmetric spaces

Part of: Homotopy theory Homotopy groups

Published online by Cambridge University Press:  18 April 2022

Daisuke Kishimoto Open the ORCID record for Daisuke Kishimoto[Opens in a new window] ,
Masahiro Takeda  and
Yichen Tong
Daisuke Kishimoto
Affiliation:
Department of Mathematics, Kyoto University, Kyoto 606-8502, Japan e-mails: kishimoto@math.kyushu-u.ac.jp, takeda.masahiro.87u@st.kyoto-u.ac.jp, tong.yichen.25m@st.kyoto-u.ac.jp
Masahiro Takeda
Affiliation:
Department of Mathematics, Kyoto University, Kyoto 606-8502, Japan e-mails: kishimoto@math.kyushu-u.ac.jp, takeda.masahiro.87u@st.kyoto-u.ac.jp, tong.yichen.25m@st.kyoto-u.ac.jp
Yichen Tong
Affiliation:
Department of Mathematics, Kyoto University, Kyoto 606-8502, Japan e-mails: kishimoto@math.kyushu-u.ac.jp, takeda.masahiro.87u@st.kyoto-u.ac.jp, tong.yichen.25m@st.kyoto-u.ac.jp
Get access Rights & Permissions[Opens in a new window]

Abstract

Ganea proved that the loop space of 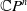$\mathbb{C} P^n$ is homotopy commutative if and only if 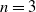$n=3$ . We generalize this result to that the loop spaces of all irreducible Hermitian symmetric spaces but 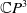$\mathbb{C} P^3$ are not homotopy commutative. The computation also applies to determining the homotopy nilpotency class of the loop spaces of generalized flag manifolds 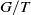$G/T$ for a maximal torus T of a compact, connected Lie group G.

MSC classification

Primary: 55P35: Loop spaces 55Q15: Whitehead products and generalizations
Type
Research Article
Information
Glasgow Mathematical Journal , First View , pp. 1 - 7
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berstein, I. and Ganea, T., Homotopical nilpotency, Illinois J. Math. 5 (1961), 99–130.CrossRefGoogle Scholar
Borel, A., and de Siebenthal, J., Les sous-groupes fermés de rang maximum des groupes de Lie clos, Comment. Math. Helv. 23 (1949), 200–221; ibid. 55 (1927), 114–134.Google Scholar
Bott, R., A note on the Samelson products in the classical groups, Comment. Math. Helv. 34 (1960), 249–256.CrossRefGoogle Scholar
Cartan, È., Sur une classe remarquable d’espaces de Riemann, Bull. Soc. Math. France 54 (1926), 214–264.CrossRefGoogle Scholar
Cartan, È., Sur les domaines borns homogènes de l’espace den variables complexes, Abh. Math. Sem. Hamburg 11 (1935), 116–162.CrossRefGoogle Scholar
Conlon, L., On the topology of EIII and EIV, Proc. Amer. Math. Soc. 16(4) (1965), 575–581.CrossRefGoogle Scholar
Félix, Y., Halperin, S. and Thomas, J.-C., Rational homotopy theory , Graduate Texts in Mathematics, vol. 205 (Springer, New York, 2001).Google Scholar
Ganea, T., On the loop spaces of projective spaces, J. Math. Mech. 16 (1967), 853–858.Google Scholar
Golasiński, M., Homotopy nilpotency of some homogeneous spaces, Manuscripta Math. 167 (2022), 245–261.CrossRefGoogle Scholar
Hamanaka, H. and Kono, A., A note on the Samelson products in $\pi_*(\mathrm{SO}(2n))$ and the group $[\mathrm{SO}(2n),\mathrm{SO}(2n)]$ , Topol. Appl. 154(3) (2007), 567–572.CrossRefGoogle Scholar
Hamanaka, H. and Kono, A., A note on Samelson products and mod p cohomology of classifying spaces of the exceptional Lie groups, Topol. Appl. 157(2) (2010), 393–400.CrossRefGoogle Scholar
Hasui, S., Kishimoto, D., Miyauchi, T. and Ohsita, A., Samelson products in quasi-p-regular exceptional Lie groups, Homol. Homotopy Appl. 20(1) (2018), 185–208.CrossRefGoogle Scholar
Hasui, S., Kishimoto, D. and Ohsita, A., Samelson products in p-regular exceptional Lie groups, Topol. Appl. 178(1) (2014), 17–29.CrossRefGoogle Scholar
Hopkins, M., Nilpotence and finite H-spaces, Israel J. Math. 66 (1989), 238–246.CrossRefGoogle Scholar
Hubbuck, J. R., On homotopy commutative H-spaces, Topology 8 (1969), 119–126.CrossRefGoogle Scholar
Ishitoya, K., Squaring operations in the Hermitian symmetric spaces, J. Math. Kyoto Univ. 32(1) (1992), 235–244.Google Scholar
Kaji, S. and Kishimoto, D., Homotopy nilpotency in p-regular loop spaces, Math. Z. 264(1) (2010), 209–224.CrossRefGoogle Scholar
Kishimoto, D. and Miyauchi, T., Higher homotopy associativity in the Harris decomposition of Lie groups, Proc. R. Soc. Edinburgh Sect. A 150(6) (2020), 2982–3000.CrossRefGoogle Scholar
Kishimoto, D., Ohsita, A. and Takeda, M., Note on Samelson products in exceptional Lie groups, Glasg. Math. J. 63(3) (2021), 741–752.CrossRefGoogle Scholar
Kishimoto, D. and Tsutaya, M., Samelson products in p-regular SO(2n) and its homotopy normality, Glasg. Math. J. 60(1) (2018), 165–174.CrossRefGoogle Scholar
Kono, A. and Ōshima, H., Commutativity of the group of self-homotopy classes of Lie groups, Bull. London Math. Soc. 36 (2004), 37–52.CrossRefGoogle Scholar
Mimura, M. and Toda, H., Topology of Lie groups, I and II , Translations of Mathematical Monographs, vol. 91 (AMS, Providence, RI, 1991)Google Scholar
Ōshima, H., Whitehead products in Stiefel manifolds and Samelson products in classical groups, Adv. Stud. Pure Math. 9 (1986), 237–258.Google Scholar
Shay, P. B., mod p Wu formulas for the Steenrod algebra and the Dyer-Lashof algebra, Proc. Amer. Math. Soc. 63 (1977), 339–347.Google Scholar
Sondow, J., Ramanujan primes and Bertrand’s postulate, Am. Math. Mon. 116(7) (2009), 630–635.CrossRefGoogle Scholar
Tsutaya, M., Higher homotopy normalities in topological groups, https://arxiv.org/abs/2111.15096.Google Scholar
Watanabe, T., The integral cohomology ring of the symmetric space EVII, J. Math. Kyoto Univ. 15(2) (1975), 363–385.Google Scholar
Zabrodsky, A., Hopf spaces (North-Holland Publishing Company, Amsterdam, 1976).Google Scholar

Save article to Kindle

To save this article to your Kindle, first ensure coreplatform@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.

Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Homotopy commutativity in Hermitian symmetric spaces
Available formats
×

Save article to Dropbox

To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.

Homotopy commutativity in Hermitian symmetric spaces
Available formats
×

Save article to Google Drive

To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.

Homotopy commutativity in Hermitian symmetric spaces
Available formats
×
×

Reply to: Submit a response

Please enter your response.

Your details

Please enter a valid email address.

Conflicting interests

Do you have any conflicting interests? *