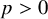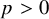1. Introduction
1.1. The mystery of fundamental groups in positive characteristic
1.1.1.
Let k be an algebraically closed field of characteristic
![]() $p\geq 0$
, and let
$p\geq 0$
, and let
![]() $(X, D_{X})$
be a smooth pointed stable curve of type
$(X, D_{X})$
be a smooth pointed stable curve of type
![]() $(g_{X}, n_{X})$
over k (i.e.,
$(g_{X}, n_{X})$
over k (i.e.,
![]() $2g_{X}+n_{X}-2>0$
, see [Reference KnudsenK, Definition 1.1 (iv)]), where X denotes the underlying curve,
$2g_{X}+n_{X}-2>0$
, see [Reference KnudsenK, Definition 1.1 (iv)]), where X denotes the underlying curve,
![]() $D_{X}$
denotes the (ordered) finite set of marked points,
$D_{X}$
denotes the (ordered) finite set of marked points,
![]() $g_{X}$
denotes the genus of X, and
$g_{X}$
denotes the genus of X, and
![]() $n_{X}$
denotes the cardinality
$n_{X}$
denotes the cardinality
![]() $\#(D_{X})$
of
$\#(D_{X})$
of
![]() $D_{X}$
. We put
$D_{X}$
. We put
![]() $U_{X}\stackrel {\mathrm {def}}{=} X \setminus D_{X}$
. By choosing a base point of
$U_{X}\stackrel {\mathrm {def}}{=} X \setminus D_{X}$
. By choosing a base point of
![]() $U_{X}$
, we have the tame fundamental group
$U_{X}$
, we have the tame fundamental group
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
of
${\pi }_{1}^{\mathrm {t}}(U_{X})$
of
![]() $U_{X}$
.
$U_{X}$
.
If
![]() $p=0$
, it is well-known that the structure of
$p=0$
, it is well-known that the structure of
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
is isomorphic to the profinite completion of the topological fundamental group of a Riemann surface of type
${\pi }_{1}^{\mathrm {t}}(U_{X})$
is isomorphic to the profinite completion of the topological fundamental group of a Riemann surface of type
![]() $(g_{X}, n_{X})$
. Hence, almost no geometric information about
$(g_{X}, n_{X})$
. Hence, almost no geometric information about
![]() $U_{X}$
can be carried out from
$U_{X}$
can be carried out from
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
. By contrast, if
${\pi }_{1}^{\mathrm {t}}(U_{X})$
. By contrast, if
![]() $p>0$
, the situation is quite different from that in characteristic
$p>0$
, the situation is quite different from that in characteristic
![]() $0$
. The tame fundamental group
$0$
. The tame fundamental group
![]() ${\pi }_{1}^{\mathrm { t}}(U_{X})$
contains rich geometric information of
${\pi }_{1}^{\mathrm { t}}(U_{X})$
contains rich geometric information of
![]() $(X, D_{X})$
, moreover, there exist anabelian phenomena for curves over algebraically closed fields of characteristic
$(X, D_{X})$
, moreover, there exist anabelian phenomena for curves over algebraically closed fields of characteristic
![]() $p>0$
.
$p>0$
.
1.1.2.
Firstly, let us explain some general background about anabelian geometry. In the 1980s, Grothendieck suggested a theory of arithmetic geometry called anabelian geometry ([Reference Grothendieck, Schneps and LochakG]). The central question of the theory is as follows: Can we reconstruct the geometric information of a variety group-theoretically from various versions of its algebraic fundamental group? The original anabelian geometry suggested by Grothendieck focused on varieties over arithmetic fields, in particular, the fields finitely generated over
![]() $\mathbb {Q}$
. In the case of curves in characteristic
$\mathbb {Q}$
. In the case of curves in characteristic
![]() $0$
, anabelian geometry has been deeply studied (e.g. [Reference NakamuraN], [Reference TamagawaT1]) and, in particular, the most important case (i.e., the fields finitely generated over
$0$
, anabelian geometry has been deeply studied (e.g. [Reference NakamuraN], [Reference TamagawaT1]) and, in particular, the most important case (i.e., the fields finitely generated over
![]() $\mathbb {Q}$
, or more general, sub-p-adic fields) has been completely established ([Reference MochizukiM]). Note that the actions of the Galois groups of the base fields on the geometric fundamental groups play a crucial role for recovering geometric information of curves over arithmetic fields.
$\mathbb {Q}$
, or more general, sub-p-adic fields) has been completely established ([Reference MochizukiM]). Note that the actions of the Galois groups of the base fields on the geometric fundamental groups play a crucial role for recovering geometric information of curves over arithmetic fields.
Next, we return to the case where k is an algebraically closed field of characteristic
![]() $p>0$
. In [Reference TamagawaT2], Tamagawa discovered that there also exist anabelian phenomena for curves over algebraically closed fields of characteristic p. This came rather surprisingly since it means that, in positive characteristic, the geometry of curves can be only determined by their geometric fundamental groups without Galois actions. Since the late 1990s, this kind of anabelian phenomenon has been studied further by Raynaud ([Reference RaynaudR2]), Pop-M. Saïdi ([Reference Pop and SaïdiPS]), Tamagawa ([Reference TamagawaT2], [Reference TamagawaT4], [Reference TamagawaT5]), and the second author of the present paper ([Reference YangY1], [Reference YangY2], [Reference YangY4]). More precisely, they focused on the so-called Weak Isom-version of Grothendieck’s anabelian conjecture for curves over algebraically closed fields of characteristic
$p>0$
. In [Reference TamagawaT2], Tamagawa discovered that there also exist anabelian phenomena for curves over algebraically closed fields of characteristic p. This came rather surprisingly since it means that, in positive characteristic, the geometry of curves can be only determined by their geometric fundamental groups without Galois actions. Since the late 1990s, this kind of anabelian phenomenon has been studied further by Raynaud ([Reference RaynaudR2]), Pop-M. Saïdi ([Reference Pop and SaïdiPS]), Tamagawa ([Reference TamagawaT2], [Reference TamagawaT4], [Reference TamagawaT5]), and the second author of the present paper ([Reference YangY1], [Reference YangY2], [Reference YangY4]). More precisely, they focused on the so-called Weak Isom-version of Grothendieck’s anabelian conjecture for curves over algebraically closed fields of characteristic
![]() $p>0$
(or the “Weak Isom-version Conjecture” for short) formulated by Tamagawa ([Reference TamagawaT3, Conjecture 2.2]) which says that curves are isomorphic if and only if their tame (or étale) fundamental groups are isomorphic. At present, this conjecture is still wide open.
$p>0$
(or the “Weak Isom-version Conjecture” for short) formulated by Tamagawa ([Reference TamagawaT3, Conjecture 2.2]) which says that curves are isomorphic if and only if their tame (or étale) fundamental groups are isomorphic. At present, this conjecture is still wide open.
1.2. Reconstructions of moduli spaces of curves via anabelian geometry
In the present paper, we study a new kind of anabelian phenomenon concerning curves over algebraically closed fields of characteristic
![]() $p>0$
, which shows that the topological structures of moduli spaces of curves can be understood by their fundamental groups.
$p>0$
, which shows that the topological structures of moduli spaces of curves can be understood by their fundamental groups.
1.2.1.
Let
![]() $\mathbb {F}_{p}$
be the prime field of characteristic
$\mathbb {F}_{p}$
be the prime field of characteristic
![]() $p>0$
, and let
$p>0$
, and let
![]() $\mathcal {M}_{g, n, \mathbb {Z}}^{\mathrm {ord}}$
be the moduli stack over
$\mathcal {M}_{g, n, \mathbb {Z}}^{\mathrm {ord}}$
be the moduli stack over
![]() $\mathbb {Z}$
parameterizing smooth n-pointed stable curves of type
$\mathbb {Z}$
parameterizing smooth n-pointed stable curves of type
![]() $(g, n)$
(in the sense of [Reference KnudsenK]). We put
$(g, n)$
(in the sense of [Reference KnudsenK]). We put
![]() $\mathcal {M}^{\mathrm {ord}}_{g, n, \mathbb {F}_{p}}\stackrel {\mathrm {def}}{=} \mathcal {M}^{\mathrm {ord}}_{g, n, \mathbb {Z}} \times _{\mathbb {Z}} \mathbb {F}_{p}$
. Note that the set of marked points of an n-smooth pointed stable curve admits a natural action of the n-symmetric group
$\mathcal {M}^{\mathrm {ord}}_{g, n, \mathbb {F}_{p}}\stackrel {\mathrm {def}}{=} \mathcal {M}^{\mathrm {ord}}_{g, n, \mathbb {Z}} \times _{\mathbb {Z}} \mathbb {F}_{p}$
. Note that the set of marked points of an n-smooth pointed stable curve admits a natural action of the n-symmetric group
![]() $S_{n}$
. Moreover, we denote by
$S_{n}$
. Moreover, we denote by
![]() $\mathcal {M}_{g, n, \mathbb {F}_{p}}\stackrel {\mathrm {def}}{=} [\mathcal {M}^{\mathrm {ord}}_{g, n, \mathbb {F}_{p}}/S_{n}]$
the quotient stack, and denote by
$\mathcal {M}_{g, n, \mathbb {F}_{p}}\stackrel {\mathrm {def}}{=} [\mathcal {M}^{\mathrm {ord}}_{g, n, \mathbb {F}_{p}}/S_{n}]$
the quotient stack, and denote by
![]() $M_{g, n, \mathbb {F}_{p}}$
the coarse moduli space of
$M_{g, n, \mathbb {F}_{p}}$
the coarse moduli space of
![]() $\mathcal {M}_{g, n, \mathbb {F}_{p}}$
.
$\mathcal {M}_{g, n, \mathbb {F}_{p}}$
.
Let
![]() $q \in M_{g, n, \mathbb {F}_{p}}$
be an arbitrary point,
$q \in M_{g, n, \mathbb {F}_{p}}$
be an arbitrary point,
![]() $k(q)$
the residue field of q,
$k(q)$
the residue field of q,
![]() $k_{q}$
an algebraically closed field containing
$k_{q}$
an algebraically closed field containing
![]() $k(q)$
, and
$k(q)$
, and
![]() $V_{q}\stackrel {\mathrm {def}}{=} \overline {\{q\}}$
the topological closure of
$V_{q}\stackrel {\mathrm {def}}{=} \overline {\{q\}}$
the topological closure of
![]() $\{q\}$
in
$\{q\}$
in
![]() $M_{g, n, \mathbb {F}_{p}}$
. Write
$M_{g, n, \mathbb {F}_{p}}$
. Write
![]() $(X_{k_q}, D_{X_{k_q}})$
for the smooth pointed stable curve of type
$(X_{k_q}, D_{X_{k_q}})$
for the smooth pointed stable curve of type
![]() $(g, n)$
over
$(g, n)$
over
![]() $k_{q}$
determined by the natural morphism
$k_{q}$
determined by the natural morphism
![]() $\mathrm {Spec} \, k_{q} \rightarrow M_{g, n, \mathbb {F}_{p}}$
and put
$\mathrm {Spec} \, k_{q} \rightarrow M_{g, n, \mathbb {F}_{p}}$
and put
![]() $U_{X_{k_{q}}} \stackrel {\mathrm {def}}{=} X_{k_q} \setminus D_{X_{k_q}}$
. In particular, we put
$U_{X_{k_{q}}} \stackrel {\mathrm {def}}{=} X_{k_q} \setminus D_{X_{k_q}}$
. In particular, we put
![]() $(X_{k_{q}}, D_{X_{k_{q}}})\stackrel {\mathrm {def}}{=} (X_{q}, D_{X_{q}})$
and
$(X_{k_{q}}, D_{X_{k_{q}}})\stackrel {\mathrm {def}}{=} (X_{q}, D_{X_{q}})$
and
![]() $U_{X_q}\stackrel {\mathrm {def}}{=} X_{q} \setminus D_{X_{q}}$
if
$U_{X_q}\stackrel {\mathrm {def}}{=} X_{q} \setminus D_{X_{q}}$
if
![]() $k_{q}$
is an algebraic closure of
$k_{q}$
is an algebraic closure of
![]() $k(q)$
. Since the isomorphism class of the tame fundamental group
$k(q)$
. Since the isomorphism class of the tame fundamental group
![]() $\pi ^{\mathrm {t}}_{1}(U_{X_{k_{q}}})$
depends only on q, we shall write
$\pi ^{\mathrm {t}}_{1}(U_{X_{k_{q}}})$
depends only on q, we shall write
![]() ${\pi }_{1}^{\mathrm {t}}(q)$
for the tame fundamental group
${\pi }_{1}^{\mathrm {t}}(q)$
for the tame fundamental group
![]() $\pi ^{\mathrm {t}}_{1}(U_{X_{k_{q}}})$
.
$\pi ^{\mathrm {t}}_{1}(U_{X_{k_{q}}})$
.
1.2.2.
We maintain the notation introduced above. The Weak Isom-version Conjecture of Tamagawa can be reformulated as follows:
Weak Isom-version Conjecture. Let
![]() $q_{i} \in M_{g, n, \mathbb {F}_{p}}$
,
$q_{i} \in M_{g, n, \mathbb {F}_{p}}$
,
![]() $i\in \{1,2\}$
, be an arbitrary point of
$i\in \{1,2\}$
, be an arbitrary point of
![]() $M_{g, n, \mathbb {F}_{p}}$
. The set of continuous isomorphisms of profinite groups
$M_{g, n, \mathbb {F}_{p}}$
. The set of continuous isomorphisms of profinite groups
is nonempty if and only if
![]() $V_{q_{1}}=V_{q_{2}}$
(namely,
$V_{q_{1}}=V_{q_{2}}$
(namely,
![]() $U_{X_{q_{1}}} \cong U_{X_{q_{2}}}$
as schemes).
$U_{X_{q_{1}}} \cong U_{X_{q_{2}}}$
as schemes).
The Weak Isom-version Conjecture means that moduli spaces of curves can be reconstructed “as sets” from the isomorphism classes of the tame fundamental groups of curves. This conjecture has been only confirmed by Tamagawa ([Reference TamagawaT4, Theorem 0.2]) in the case of genus
![]() $0$
, namely, the following:
$0$
, namely, the following:
Suppose that
![]() $q_{1}$
is a closed point of
$q_{1}$
is a closed point of
![]() $M_{0, n, \mathbb {F}_{p}}$
. Then, the Weak Isom-version Conjecture holds.
$M_{0, n, \mathbb {F}_{p}}$
. Then, the Weak Isom-version Conjecture holds.
Next, we pose a new conjecture as follows, which we call the Weak Hom-version of the Grothendieck conjecture for curves over algebraically closed fields of characteristic
![]() $p>0$
(=Weak Hom-version Conjecture), and which generalizes the Weak Isom-version Conjecture.
$p>0$
(=Weak Hom-version Conjecture), and which generalizes the Weak Isom-version Conjecture.
Weak Hom-version Conjecture. Let
![]() $q_{i} \in M_{g, n, \mathbb {F}_{p}}$
,
$q_{i} \in M_{g, n, \mathbb {F}_{p}}$
,
![]() $i\in \{1,2\}$
, be an arbitrary point of
$i\in \{1,2\}$
, be an arbitrary point of
![]() $M_{g, n, \mathbb {F}_{p}}$
. The set of open continuous homomorphisms of profinite groups
$M_{g, n, \mathbb {F}_{p}}$
. The set of open continuous homomorphisms of profinite groups
is nonempty if and only if
![]() $V_{q_{1}}\supseteq V_{q_{2}}.$
$V_{q_{1}}\supseteq V_{q_{2}}.$
Roughly speaking, this means that a smooth pointed stable curve corresponding to a geometric point over
![]() $q_{2}$
can be deformed to a smooth pointed stable curve corresponding to a geometric point over
$q_{2}$
can be deformed to a smooth pointed stable curve corresponding to a geometric point over
![]() $q_{1}$
if and only if the set of open continuous homomorphisms of tame fundamental groups
$q_{1}$
if and only if the set of open continuous homomorphisms of tame fundamental groups
![]() $\text {Hom}_{\text {pg}}^{\mathrm {op}}({\pi }_{1}^{\mathrm {t}}(q_{1}), {\pi }_{1}^{\mathrm {t}}(q_{2}))$
is not empty.
$\text {Hom}_{\text {pg}}^{\mathrm {op}}({\pi }_{1}^{\mathrm {t}}(q_{1}), {\pi }_{1}^{\mathrm {t}}(q_{2}))$
is not empty.
The Weak Hom-version Conjecture means that the sets of deformations of a smooth pointed stable curve can be reconstructed group-theoretically from the sets of open continuous homomorphisms of their tame fundamental groups. Therefore, it provides a new kind of anabelian phenomenon:
The moduli spaces of curves in positive characteristic can be understood not only as sets but also “as topological spaces” from the sets of open continuous homomorphisms of tame fundamental groups of curves in positive characteristic.
1.3. Main result
1.3.1.
The main result of the present paper confirms the Weak Hom-version Conjecture for curves of genus
![]() $0$
(see Theorem 4.4 (iv) for a more general statement):
$0$
(see Theorem 4.4 (iv) for a more general statement):
Theorem 1.1. The Weak Hom-version Conjecture holds when
![]() $q_{1}$
is a closed point of
$q_{1}$
is a closed point of
![]() $M_{0, n, \mathbb {F}_{p}}$
.
$M_{0, n, \mathbb {F}_{p}}$
.
Theorem 1.1 follows from the following “Hom-type” anabelian result (see Theorem 4.3 for a more precise statement), which is a generalization of Tamagawa’s result (i.e. [Reference TamagawaT4, Theorem 0.2]):
Theorem 1.2. Let
![]() $q_{1} \in M_{g, n, \mathbb {F}_{p}}$
be a closed point and
$q_{1} \in M_{g, n, \mathbb {F}_{p}}$
be a closed point and
![]() $q_{2}\in M_{g, n, \mathbb {F}_{p}}$
an arbitrary point. Then the set of open continuous homomorphisms
$q_{2}\in M_{g, n, \mathbb {F}_{p}}$
an arbitrary point. Then the set of open continuous homomorphisms
is nonempty if and only if
![]() $U_{X_{q_1}} \cong U_{X_{q_2}}$
as schemes.
$U_{X_{q_1}} \cong U_{X_{q_2}}$
as schemes.
Remark
Note that Theorem 1.2 is essentially different from [Reference TamagawaT4, Theorem 0.2]. The reason is the following: We do not know whether or not
is nonempty when
![]() $\mathrm {Hom}^{\mathrm {op}}_{\mathrm {pg}}({\pi }_{1}^{\mathrm {t}}(q_{1}), {\pi }_{1}^{\mathrm {t}}(q_{2}))$
is nonempty.
$\mathrm {Hom}^{\mathrm {op}}_{\mathrm {pg}}({\pi }_{1}^{\mathrm {t}}(q_{1}), {\pi }_{1}^{\mathrm {t}}(q_{2}))$
is nonempty.
On the other hand, to verify Theorem 1.2, we need to establish various anabelian reconstructions from open continuous homomorphisms of tame fundamental groups, which are much harder than the case of isomorphisms in general. We explain in more detail about this point in the reminder of the Introduction.
1.3.2.
Let us explain the main differences between the proofs of Tamagawa’s result (i.e. [Reference TamagawaT4, Theorem 0.2]) and our result (i.e., Theorem 1.2), and new ingredients of our proof. First, we recall the key points of the proof of Tamagawa’s result. Roughly speaking, Tamagawa’s proof consists of two parts:
-
(1) He proved that the sets of inertia subgroups of marked points and the field structures associated to inertia subgroups of marked points of smooth pointed stable curves can be reconstructed group-theoretically from tame fundamental groups. This is the most difficult part of Tamagawa’s proof.
-
(2) By using the inertia subgroups and their associated field structures, if
 $g=0$
, he proved that the coordinates of marked points can be calculated group-theoretically.
$g=0$
, he proved that the coordinates of marked points can be calculated group-theoretically.
The group-theoretical reconstructions in Tamagawa’s proofs (1) and (2) are isomorphic version reconstructions. This means that the reconstructions should fix an isomorphism class of a tame fundamental group. To explain this, let us show an example. Let
![]() $U_{X_{i}}$
,
$U_{X_{i}}$
,
![]() $i\in \{1, 2\}$
, be a curve of type
$i\in \{1, 2\}$
, be a curve of type
![]() $(g_{X}, n_{X})$
over an algebraically closed field k of characteristic
$(g_{X}, n_{X})$
over an algebraically closed field k of characteristic
![]() $p>0$
introduced above,
$p>0$
introduced above,
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
the tame fundamental group of
${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
the tame fundamental group of
![]() $U_{X_{i}}$
,
$U_{X_{i}}$
,
![]() $\phi : {\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \rightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
an open continuous homomorphism,
$\phi : {\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \rightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
an open continuous homomorphism,
![]() $H_{2} \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
an open subgroup, and
$H_{2} \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
an open subgroup, and
![]() $H_{1}\stackrel {\mathrm {def}}{=} \phi ^{-1}(H_{2})$
. In Tamagawa’s proof, since
$H_{1}\stackrel {\mathrm {def}}{=} \phi ^{-1}(H_{2})$
. In Tamagawa’s proof, since
![]() $\phi $
is an isomorphism, we have
$\phi $
is an isomorphism, we have
![]() $H_{1} \cong H_{2}$
. Then the group-theoretical reconstruction for types implies that the type
$H_{1} \cong H_{2}$
. Then the group-theoretical reconstruction for types implies that the type
![]() $(g_{X_{H_{1}}}, n_{X_{H_{1}}})$
and the type
$(g_{X_{H_{1}}}, n_{X_{H_{1}}})$
and the type
![]() $(g_{X_{H_{2}}}, n_{X_{H_{2}}})$
of the curves corresponding to
$(g_{X_{H_{2}}}, n_{X_{H_{2}}})$
of the curves corresponding to
![]() $H_{1}$
and
$H_{1}$
and
![]() $H_{2}$
, respectively, are equal. This is a key point in the proof of Tamagawa’s group-theoretical reconstruction of the inertia subgroups of marked points. On the other hand, his method cannot be applied to the present paper. The reason is that we need to treat the case where
$H_{2}$
, respectively, are equal. This is a key point in the proof of Tamagawa’s group-theoretical reconstruction of the inertia subgroups of marked points. On the other hand, his method cannot be applied to the present paper. The reason is that we need to treat the case where
![]() $\phi $
is an arbitrary open continuous homomorphism. Since
$\phi $
is an arbitrary open continuous homomorphism. Since
![]() $H_{1}$
is not isomorphic to
$H_{1}$
is not isomorphic to
![]() $H_{2}$
in general (e.g., specialization homomorphism), we do not know whether or not
$H_{2}$
in general (e.g., specialization homomorphism), we do not know whether or not
![]() $(g_{X_{H_{1}}}, n_{X_{H_{1}}})=(g_{X_{H_{2}}}, n_{X_{H_{2}}}).$
This is one of the main difficulties of “Hom-type” problems appearing in anabelian geometry. Similar difficulties for generalized Hasse-Witt invariants will appear if we try to reconstruct the field structure associated to inertia subgroups of marked points.
$(g_{X_{H_{1}}}, n_{X_{H_{1}}})=(g_{X_{H_{2}}}, n_{X_{H_{2}}}).$
This is one of the main difficulties of “Hom-type” problems appearing in anabelian geometry. Similar difficulties for generalized Hasse-Witt invariants will appear if we try to reconstruct the field structure associated to inertia subgroups of marked points.
To overcome the difficulties mentioned above, we have the following key observation:
The inequalities of
![]() $\text {Avr}_{p}(H_{i})$
(i.e., the p-averages of generalized Hasse-Witt invariants (see Section 3.4.3)) induced by
$\text {Avr}_{p}(H_{i})$
(i.e., the p-averages of generalized Hasse-Witt invariants (see Section 3.4.3)) induced by
![]() $\phi $
play roles of the comparability of (outer) Galois representations in the theory of anabelian geometry of curves over algebraically closed fields of characteristic
$\phi $
play roles of the comparability of (outer) Galois representations in the theory of anabelian geometry of curves over algebraically closed fields of characteristic
![]() $p> 0$
.
$p> 0$
.
In the present paper, our method for reconstructing inertia subgroups of marked points is completely different from Tamagawa’s reconstruction. We develop a new group-theoretical algorithm for reconstructing the inertia subgroups of marked points whose input datum is a profinite group which is isomorphic to
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
,
${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
,
![]() $i\in \{1, 2\}$
, and whose output data are inertia subgroups of marked points (Theorem 3.14). Moreover, we prove that the group-theoretical algorithm and the reconstructions for field structures are compatible with arbitrary surjection
$i\in \{1, 2\}$
, and whose output data are inertia subgroups of marked points (Theorem 3.14). Moreover, we prove that the group-theoretical algorithm and the reconstructions for field structures are compatible with arbitrary surjection
![]() $\phi $
(Proposition 3.15). By using Theorem 3.14 and Proposition 3.15, we may prove that Tamagawa’s calculation of coordinates is compatible with our reconstructions. This implies Theorem 1.2.
$\phi $
(Proposition 3.15). By using Theorem 3.14 and Proposition 3.15, we may prove that Tamagawa’s calculation of coordinates is compatible with our reconstructions. This implies Theorem 1.2.
1.4. Some further developments
1.4.1. Moduli spaces of fundamental groups
Let us explain some further developments for the anabelian phenomenon concerning the Weak Hom-version Conjecture. In [Reference YangY6], the second author of the present paper introduced a topological space
![]() $\Pi _{g,n}$
(or more general,
$\Pi _{g,n}$
(or more general,
![]() $\overline \Pi _{g, n}$
) determined group-theoretically by the tame fundamental groups of smooth pointed stable curves (or more general, the geometric log étale fundamental groups of arbitrary pointed stable curves) of type
$\overline \Pi _{g, n}$
) determined group-theoretically by the tame fundamental groups of smooth pointed stable curves (or more general, the geometric log étale fundamental groups of arbitrary pointed stable curves) of type
![]() $(g, n)$
which he called moduli spaces of fundamental groups of curves, whose underlying set is the sets of isomorphism classes of fundamental groups, and whose topology is determined by the sets of finite quotients of fundamental groups. Moreover, he posed the so-called homeomorphism conjecture, roughly speaking, which says that (by quotienting a certain equivalence relation induced by Frobenius actions) the moduli spaces of curves are homeomorphic to the moduli spaces of fundamental groups.
$(g, n)$
which he called moduli spaces of fundamental groups of curves, whose underlying set is the sets of isomorphism classes of fundamental groups, and whose topology is determined by the sets of finite quotients of fundamental groups. Moreover, he posed the so-called homeomorphism conjecture, roughly speaking, which says that (by quotienting a certain equivalence relation induced by Frobenius actions) the moduli spaces of curves are homeomorphic to the moduli spaces of fundamental groups.
In the present literature, the term “anabelian” is understood to mean that a geometric object can be determined by its fundamental group. On the other hand, the homeomorphism conjecture concerning moduli spaces of fundamental groups supplies a new point of view to understand anabelian phenomena as follows:
The term “anabelian” means that not only a geometric object can be determined by its fundamental groups, but also a certain moduli space of geometric objects can be determined by the fundamental groups of geometric objects.
Under this point of view, the homeomorphism conjecture is reminiscent of a famous theorem in the theory of classic Teichmüller spaces which state that the Teichmüller spaces of complex hyperbolic curves are homeomorphic to the spaces of discrete and faithful representations of topological fundamental groups of underlying surfaces into the group
![]() $PSL_{2}(\mathbb {R})$
.
$PSL_{2}(\mathbb {R})$
.
In fact, Theorem 1.1 implies that
![]() $M_{0, 4, \mathbb {F}_{p}}$
is homeomorphic to
$M_{0, 4, \mathbb {F}_{p}}$
is homeomorphic to
![]() $\Pi _{0,4}$
as topological spaces (note that Tamagawa’s result (i.e. [Reference TamagawaT4, Theorem 0.2]) only says that the natural map
$\Pi _{0,4}$
as topological spaces (note that Tamagawa’s result (i.e. [Reference TamagawaT4, Theorem 0.2]) only says that the natural map
![]() $M_{0, 4, \mathbb {F}_{p}} \rightarrow \Pi _{0,4}$
is a bijection as sets). Based on [Reference YangY1], [Reference YangY3], [Reference YangY4], [Reference YangY5], and the main results of the present paper, the main results of [Reference YangY6] and [Reference YangY7] say that the homeomorphism conjecture holds for
$M_{0, 4, \mathbb {F}_{p}} \rightarrow \Pi _{0,4}$
is a bijection as sets). Based on [Reference YangY1], [Reference YangY3], [Reference YangY4], [Reference YangY5], and the main results of the present paper, the main results of [Reference YangY6] and [Reference YangY7] say that the homeomorphism conjecture holds for
![]() $1$
-dimensional moduli spaces of pointed stable curves. Moreover, the Weak Hom-version Conjecture and the pointed collection conjecture (see Section 2.2 of the present paper) are main steps toward the homeomorphism conjecture for higher dimensional moduli spaces of curves (see [Reference YangY8, Section 1.2.3]).
$1$
-dimensional moduli spaces of pointed stable curves. Moreover, the Weak Hom-version Conjecture and the pointed collection conjecture (see Section 2.2 of the present paper) are main steps toward the homeomorphism conjecture for higher dimensional moduli spaces of curves (see [Reference YangY8, Section 1.2.3]).
1.4.2. The sets of finite quotients of tame fundamental groups
We maintain the notation introduced in Section 1.1.1. The techniques developed in Section 3 of the present paper have important applications for understanding the set of finite quotients
![]() ${\pi }_{A}^{\mathrm {t}}(U_{X})$
of the tame fundamental groups
${\pi }_{A}^{\mathrm {t}}(U_{X})$
of the tame fundamental groups
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
of
${\pi }_{1}^{\mathrm {t}}(U_{X})$
of
![]() $U_{X}$
. *Note that, if
$U_{X}$
. *Note that, if
![]() $U_{X}$
is affine, the set
$U_{X}$
is affine, the set
![]() ${\pi }_{A}^{\text {'et}}(U_{X})$
of finite quotients of the étale fundamental groups
${\pi }_{A}^{\text {'et}}(U_{X})$
of finite quotients of the étale fundamental groups
![]() ${\pi }_{1}^{\text {'et}}(U_{X})$
of
${\pi }_{1}^{\text {'et}}(U_{X})$
of
![]() $U_{X}$
can be completely determined by its type
$U_{X}$
can be completely determined by its type
![]() $(g_{X}, n_{X})$
(i.e., Abhyankar’s conjecture proved by Raynaud for affine lines and Harbater in general). However, the structure of
$(g_{X}, n_{X})$
(i.e., Abhyankar’s conjecture proved by Raynaud for affine lines and Harbater in general). However, the structure of
![]() ${\pi }_{1}^{\text {'et}}(U_{X})$
cannot be carried out from
${\pi }_{1}^{\text {'et}}(U_{X})$
cannot be carried out from
![]() ${\pi }_{A}^{\text {'et}}(U_{X})$
since
${\pi }_{A}^{\text {'et}}(U_{X})$
since
![]() ${\pi }_{1}^{\text {'et}}(U_{X})$
is not topologically finitely generated when
${\pi }_{1}^{\text {'et}}(U_{X})$
is not topologically finitely generated when
![]() $U_{X}$
is affine.
$U_{X}$
is affine.
By contrast, the isomorphism class of
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
can be completely determined by
${\pi }_{1}^{\mathrm {t}}(U_{X})$
can be completely determined by
![]() ${\pi }_{A}^{\mathrm {t}}(U_{X})$
since
${\pi }_{A}^{\mathrm {t}}(U_{X})$
since
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
is topologically finitely generated, and one cannot expect that there exists an explicit description for the entire set
${\pi }_{1}^{\mathrm {t}}(U_{X})$
is topologically finitely generated, and one cannot expect that there exists an explicit description for the entire set
![]() ${\pi }_{A}^{\mathrm {t}}(U_{X})$
since there exists anabelian phenomenon mentioned above (i.e.,
${\pi }_{A}^{\mathrm {t}}(U_{X})$
since there exists anabelian phenomenon mentioned above (i.e.,
![]() ${\pi }_{A}^{\mathrm {t}}(U_{X})$
depends on the isomorphism class of
${\pi }_{A}^{\mathrm {t}}(U_{X})$
depends on the isomorphism class of
![]() $U_{X}$
). On the other hand, for understanding more precisely the relationship between the structures of tame fundamental groups and the anabelian phenomena in positive characteristic world, it is natural to ask the following interesting problem:
$U_{X}$
). On the other hand, for understanding more precisely the relationship between the structures of tame fundamental groups and the anabelian phenomena in positive characteristic world, it is natural to ask the following interesting problem:
How does the scheme structure of
![]() $U_{X}$
affect explicitly the set of finite quotients
$U_{X}$
affect explicitly the set of finite quotients
![]() ${\pi }_{A}^{\mathrm {t}}(U_{X})$
?
${\pi }_{A}^{\mathrm {t}}(U_{X})$
?
In [Reference YangY9], by applying the techniques developed in Section 3 of the present paper and [Reference YangY5, Theorem 1.2], we obtain the following interesting generalization of [Reference TamagawaT4, Theorem 0.2] (i.e., a “finite version” of the Weak Isom-version Conjecture):
Let
![]() $q_{1}\in M_{g_{1}, n_{1}, \mathbb {F}_{p}}$
and
$q_{1}\in M_{g_{1}, n_{1}, \mathbb {F}_{p}}$
and
![]() $q_{2}\in M_{0, n_{2}, \mathbb {F}_{p}}$
be arbitrary points and
$q_{2}\in M_{0, n_{2}, \mathbb {F}_{p}}$
be arbitrary points and
![]() ${\pi }_{A}^{\mathrm {t}}(q_{i})$
the set of finite quotients of the tame fundamental group
${\pi }_{A}^{\mathrm {t}}(q_{i})$
the set of finite quotients of the tame fundamental group
![]() ${\pi }_{1}^{\mathrm { t}}(q_{i})$
. Suppose that
${\pi }_{1}^{\mathrm { t}}(q_{i})$
. Suppose that
![]() $q_{2}$
is a closed point of
$q_{2}$
is a closed point of
![]() $M_{0, n_{2}, \mathbb {F}_{p}}$
. Then we can construct explicitly a finite group G depending on
$M_{0, n_{2}, \mathbb {F}_{p}}$
. Then we can construct explicitly a finite group G depending on
![]() $q_{1}$
and
$q_{1}$
and
![]() $q_{2}$
such that
$q_{2}$
such that
![]() $U_{X_{q_{1}}} \cong U_{X_{q_{2}}}$
as schemes if and only if
$U_{X_{q_{1}}} \cong U_{X_{q_{2}}}$
as schemes if and only if
![]() $G\in {\pi }_{A}^{\mathrm {t}}(q_{1}) \cap {\pi }_{A}^{\mathrm {t}}(q_{2})$
. In particular, if
$G\in {\pi }_{A}^{\mathrm {t}}(q_{1}) \cap {\pi }_{A}^{\mathrm {t}}(q_{2})$
. In particular, if
![]() $\pi ^{\mathrm {t}}_{1}(q_{1}) \not \cong {\pi }_{1}^{\mathrm {t}}(q_{2})$
, then we can construct explicitly a finite group G depending on
$\pi ^{\mathrm {t}}_{1}(q_{1}) \not \cong {\pi }_{1}^{\mathrm {t}}(q_{2})$
, then we can construct explicitly a finite group G depending on
![]() $q_{1}$
and
$q_{1}$
and
![]() $q_{2}$
such that
$q_{2}$
such that
![]() $G \in {\pi }_{A}^{\mathrm {t}}(q_{1})$
and
$G \in {\pi }_{A}^{\mathrm {t}}(q_{1})$
and
![]() $G \not \in {\pi }_{A}^{\mathrm {t}}(q_{2})$
.
$G \not \in {\pi }_{A}^{\mathrm {t}}(q_{2})$
.
1.5. Structure of the present paper
The present paper is organized as follows. In Section 2, we formulate the Weak Hom-version Conjecture and the pointed collection conjecture. In Section 3, we give a group-theoretical algorithm for reconstructions of inertia subgroups associated marked points, and prove that the group-theoretical algorithm is compatible with arbitrary open surjective homomorphisms of tame fundamental groups. In Section 4, we prove our main results.
2. Conjectures
In this section, we formulate two new conjectures concerning anabelian geometry of curves over algebraically closed fields of characteristic
![]() $p>0$
.
$p>0$
.
2.1. The Weak Hom-version Conjecture
In this subsection, we formulate the first conjecture of the present paper, which we call “the Weak Hom-version Conjecture.”
2.1.1.
Let k be an algebraically closed field of characteristic
![]() $p>0$
, and let
$p>0$
, and let
be a smooth pointed stable curve of type
![]() $(g_{X}, n_{X})$
over k, where X denotes the (smooth) underlying curve of genus
$(g_{X}, n_{X})$
over k, where X denotes the (smooth) underlying curve of genus
![]() $g_{X}$
and
$g_{X}$
and
![]() $D_{X}$
denotes the (ordered) finite set of marked points with cardinality
$D_{X}$
denotes the (ordered) finite set of marked points with cardinality
![]() $n_{X}\stackrel {\mathrm {def}}{=} \#(D_{X})$
satisfying [Reference KnudsenK, Definition 1.1 (iv)] (i.e.,
$n_{X}\stackrel {\mathrm {def}}{=} \#(D_{X})$
satisfying [Reference KnudsenK, Definition 1.1 (iv)] (i.e.,
![]() $2g_{X}+n_{X}-2>0$
). Note that
$2g_{X}+n_{X}-2>0$
). Note that
![]() $U_{X}\stackrel {\mathrm {def}}{=} X \setminus D_{X}$
is a hyperbolic curve over k.
$U_{X}\stackrel {\mathrm {def}}{=} X \setminus D_{X}$
is a hyperbolic curve over k.
Let
![]() $(Y, D_{Y})$
and
$(Y, D_{Y})$
and
![]() $(X, D_{X})$
be smooth pointed stable curves over k, and let
$(X, D_{X})$
be smooth pointed stable curves over k, and let
![]() $f: (Y, D_{Y}) \rightarrow (X, D_{X})$
be a morphism of smooth pointed stable curves over k. We shall say that f is étale (respectively, tame, Galois étale, Galois tame) if f is étale over X (respectively, f is étale over
$f: (Y, D_{Y}) \rightarrow (X, D_{X})$
be a morphism of smooth pointed stable curves over k. We shall say that f is étale (respectively, tame, Galois étale, Galois tame) if f is étale over X (respectively, f is étale over
![]() $U_{X}$
and is at most tamely ramified over
$U_{X}$
and is at most tamely ramified over
![]() $D_{X}$
, f is a Galois covering and is étale, f is a Galois covering and is tame).
$D_{X}$
, f is a Galois covering and is étale, f is a Galois covering and is tame).
By choosing a base point of
![]() $x \in U_{X}$
, we have the tame fundamental group
$x \in U_{X}$
, we have the tame fundamental group
![]() $\pi ^{\mathrm {t}}_{1}(U_{X}, x)$
of
$\pi ^{\mathrm {t}}_{1}(U_{X}, x)$
of
![]() $U_{X}$
and the étale fundamental group
$U_{X}$
and the étale fundamental group
![]() ${\pi }_{1}(X, x)$
of X. Since we only focus on the isomorphism classes of fundamental groups in the present paper, for simplicity of notation, we omit the base point and denote by
${\pi }_{1}(X, x)$
of X. Since we only focus on the isomorphism classes of fundamental groups in the present paper, for simplicity of notation, we omit the base point and denote by
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X}) \ \text {and} \ {\pi }_{1}(X)$
the tame fundamental group
${\pi }_{1}^{\mathrm {t}}(U_{X}) \ \text {and} \ {\pi }_{1}(X)$
the tame fundamental group
![]() $\pi ^{\mathrm {t}}_{1}(U_{X}, x)$
of
$\pi ^{\mathrm {t}}_{1}(U_{X}, x)$
of
![]() $U_{X}$
and the étale fundamental group
$U_{X}$
and the étale fundamental group
![]() ${\pi }_{1}(X, x)$
of X, respectively. Note that there is a natural continuous surjective homomorphism
${\pi }_{1}(X, x)$
of X, respectively. Note that there is a natural continuous surjective homomorphism
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X}) \twoheadrightarrow {\pi }_{1}(X).$
${\pi }_{1}^{\mathrm {t}}(U_{X}) \twoheadrightarrow {\pi }_{1}(X).$
2.1.2.
Let
![]() $\overline {\mathbb {F}}_{p}$
be an algebraic closure of
$\overline {\mathbb {F}}_{p}$
be an algebraic closure of
![]() $\mathbb {F}_{p}$
, and let
$\mathbb {F}_{p}$
, and let
![]() $\mathcal {M}^{\mathrm {ord}}_{g, n, \mathbb {F}_{p}}$
be the moduli stack over
$\mathcal {M}^{\mathrm {ord}}_{g, n, \mathbb {F}_{p}}$
be the moduli stack over
![]() $\mathbb {Z}$
parameterizing smooth pointed stable curves of type
$\mathbb {Z}$
parameterizing smooth pointed stable curves of type
![]() $(g, n)$
in the sense of [Reference KnudsenK, Definition 1.1]. The set of marked points of a smooth pointed stable curve admits a natural action of the n-symmetric group
$(g, n)$
in the sense of [Reference KnudsenK, Definition 1.1]. The set of marked points of a smooth pointed stable curve admits a natural action of the n-symmetric group
![]() $S_{n}$
, we put
$S_{n}$
, we put
![]() $\mathcal {M}_{g, n, \mathbb {Z}}\stackrel {\mathrm {def}}{=} [\mathcal {M}_{g, n, \mathbb {Z}}^{\mathrm {ord}}/S_{n}]$
the quotient stack. Moreover, we denote by
$\mathcal {M}_{g, n, \mathbb {Z}}\stackrel {\mathrm {def}}{=} [\mathcal {M}_{g, n, \mathbb {Z}}^{\mathrm {ord}}/S_{n}]$
the quotient stack. Moreover, we denote by
![]() $\mathcal {M}_{g, n}^{\mathrm {ord}} \stackrel {\mathrm {def}}{=} \mathcal {M}_{g, n, \mathbb {Z}} \times _{\mathbb {Z}} \overline {\mathbb {F}}_{p}$
,
$\mathcal {M}_{g, n}^{\mathrm {ord}} \stackrel {\mathrm {def}}{=} \mathcal {M}_{g, n, \mathbb {Z}} \times _{\mathbb {Z}} \overline {\mathbb {F}}_{p}$
,
![]() $\mathcal {M}_{g, n, \mathbb {F}_{p}}\stackrel {\mathrm {def}}{=} \mathcal {M}_{g, n, \mathbb {Z}} \times _{\mathbb {Z}} \mathbb {F}_{p}$
, and
$\mathcal {M}_{g, n, \mathbb {F}_{p}}\stackrel {\mathrm {def}}{=} \mathcal {M}_{g, n, \mathbb {Z}} \times _{\mathbb {Z}} \mathbb {F}_{p}$
, and
![]() $\mathcal {M}_{g, n}\stackrel {\mathrm {def}}{=} \mathcal {M}_{g, n, \mathbb {Z}} \times _{\mathbb {Z}} \overline {\mathbb {F}}_{p}$
, and denote by
$\mathcal {M}_{g, n}\stackrel {\mathrm {def}}{=} \mathcal {M}_{g, n, \mathbb {Z}} \times _{\mathbb {Z}} \overline {\mathbb {F}}_{p}$
, and denote by
![]() $M_{g, n}^{\mathrm {ord}}$
,
$M_{g, n}^{\mathrm {ord}}$
,
![]() $M_{g, n, \mathbb {F}_{p}}$
, and
$M_{g, n, \mathbb {F}_{p}}$
, and
![]() $M_{g, n}$
the coarse moduli spaces of
$M_{g, n}$
the coarse moduli spaces of
![]() $\mathcal {M}_{g, n}^{\mathrm {ord}}$
,
$\mathcal {M}_{g, n}^{\mathrm {ord}}$
,
![]() $\mathcal {M}_{g, n, \mathbb {F}_{p}}$
, and
$\mathcal {M}_{g, n, \mathbb {F}_{p}}$
, and
![]() $\mathcal {M}_{g, n}$
, respectively.
$\mathcal {M}_{g, n}$
, respectively.
Let
![]() $q\in M_{g, n}^{\mathrm {ord}}$
be an arbitrary point and
$q\in M_{g, n}^{\mathrm {ord}}$
be an arbitrary point and
![]() $k(q)$
the residue field of q, and
$k(q)$
the residue field of q, and
![]() $k_{q}$
an algebraically closed field containing
$k_{q}$
an algebraically closed field containing
![]() $k(q)$
. Write
$k(q)$
. Write
![]() $(X_{k_q}, D_{X_{k_q}})$
for the smooth pointed stable curve of type
$(X_{k_q}, D_{X_{k_q}})$
for the smooth pointed stable curve of type
![]() $(g, n)$
over
$(g, n)$
over
![]() $k_{q}$
determined by the natural morphism
$k_{q}$
determined by the natural morphism
![]() $\mathrm {Spec} \, k_{q} \rightarrow \mathrm {Spec} \, k(q) \rightarrow M_{g, n}^{\mathrm {ord}}$
and
$\mathrm {Spec} \, k_{q} \rightarrow \mathrm {Spec} \, k(q) \rightarrow M_{g, n}^{\mathrm {ord}}$
and
![]() $U_{X_{k_q}}$
for
$U_{X_{k_q}}$
for
![]() $X_{k_q} \setminus D_{X_{k_q}}$
. In particular, if
$X_{k_q} \setminus D_{X_{k_q}}$
. In particular, if
![]() $k_{q}$
is an algebraic closure of
$k_{q}$
is an algebraic closure of
![]() $k(q)$
, we shall write
$k(q)$
, we shall write
![]() $(X_{q}, D_{X_{q}})$
for
$(X_{q}, D_{X_{q}})$
for
![]() $(X_{k_q}, D_{X_{k_q}})$
.
$(X_{k_q}, D_{X_{k_q}})$
.
Since the isomorphism class of the tame fundamental group
![]() $\pi ^{\mathrm {t}}_{1}(U_{X_{k_q}})$
depends only on q (i.e., the isomorphism class does not depend on the choices of
$\pi ^{\mathrm {t}}_{1}(U_{X_{k_q}})$
depends only on q (i.e., the isomorphism class does not depend on the choices of
![]() $k_{q}$
), we shall write
$k_{q}$
), we shall write
![]() $\pi ^{\mathrm {t}}_{1}(q) \ \text {and} \ \pi ^{\mathrm {t}}_{A}(q)$
for
$\pi ^{\mathrm {t}}_{1}(q) \ \text {and} \ \pi ^{\mathrm {t}}_{A}(q)$
for
![]() $\pi ^{\mathrm {t}}_{1}(U_{X_{k_q}})$
and the set of finite quotients of
$\pi ^{\mathrm {t}}_{1}(U_{X_{k_q}})$
and the set of finite quotients of
![]() $\pi ^{\mathrm {t}}_{1}(U_{X_{k_q}})$
, respectively. [Reference Fried and JardenFJ, Proposition 16.10.7] implies that, for any points
$\pi ^{\mathrm {t}}_{1}(U_{X_{k_q}})$
, respectively. [Reference Fried and JardenFJ, Proposition 16.10.7] implies that, for any points
![]() $q_{1}, q_{2} \in M_{g, n}^{\mathrm {ord}}$
,
$q_{1}, q_{2} \in M_{g, n}^{\mathrm {ord}}$
,
![]() $\pi ^{\mathrm {t}}_{1}(q_{1}) \cong \pi ^{\mathrm {t}}_{1}(q_{2})$
as profinite groups if and only if
$\pi ^{\mathrm {t}}_{1}(q_{1}) \cong \pi ^{\mathrm {t}}_{1}(q_{2})$
as profinite groups if and only if
![]() $\pi ^{\mathrm {t}}_{A}(q_{1})=\pi ^{\mathrm {t}}_{A}(q_{2})$
as sets.
$\pi ^{\mathrm {t}}_{A}(q_{1})=\pi ^{\mathrm {t}}_{A}(q_{2})$
as sets.
On the other hand, let
![]() $q\in M_{g, n}^{\mathrm {ord}}$
and
$q\in M_{g, n}^{\mathrm {ord}}$
and
![]() $q'\in M_{g, n, \mathbb {F}_{p}}$
be arbitrary points. We denote by
$q'\in M_{g, n, \mathbb {F}_{p}}$
be arbitrary points. We denote by
![]() $V_{q}\subseteq M_{g, n}^{\mathrm {ord}}$
and
$V_{q}\subseteq M_{g, n}^{\mathrm {ord}}$
and
![]() $V_{q'} \subseteq M_{g, n, \mathbb {F}_{p}}$
the topological closures of q and
$V_{q'} \subseteq M_{g, n, \mathbb {F}_{p}}$
the topological closures of q and
![]() $q'$
in
$q'$
in
![]() $M^{\mathrm {ord}}_{g, n}$
and
$M^{\mathrm {ord}}_{g, n}$
and
![]() $M_{g, n, \mathbb {F}_{p}}$
, respectively.
$M_{g, n, \mathbb {F}_{p}}$
, respectively.
2.1.3.
We have the following definition.
Definition 2.1. (i) Let
![]() $c_{1}, c_{2} \in M_{g, n}^{\mathrm {ord, cl}}$
be closed points, where
$c_{1}, c_{2} \in M_{g, n}^{\mathrm {ord, cl}}$
be closed points, where
![]() $(-)^{\mathrm {cl}}$
denotes the set of closed points of
$(-)^{\mathrm {cl}}$
denotes the set of closed points of
![]() $(-)$
. Then,
$(-)$
. Then,
![]() $c_{1} \sim _{fe} c_{2}$
if there exists
$c_{1} \sim _{fe} c_{2}$
if there exists
![]() $m\in \mathbb {Z}$
, such that
$m\in \mathbb {Z}$
, such that
![]() $ \nu (c_{2})=\nu (c_{1}^{(m)})$
, where
$ \nu (c_{2})=\nu (c_{1}^{(m)})$
, where
![]() $c_{1}^{(m)}$
denotes the closed point corresponding to the curve obtained by mth Frobenius twist of the curve corresponding to
$c_{1}^{(m)}$
denotes the closed point corresponding to the curve obtained by mth Frobenius twist of the curve corresponding to
![]() $c_{1}$
. Here, “fe” means “Frobenius equivalence.”
$c_{1}$
. Here, “fe” means “Frobenius equivalence.”
(ii) Let
![]() $q_{1}, q_{2} \in M_{g, n}^{\mathrm {ord}}$
be arbitrary points. We denote by
$q_{1}, q_{2} \in M_{g, n}^{\mathrm {ord}}$
be arbitrary points. We denote by
![]() $V_{q_1} \supseteq _{fe} V_{q_2}$
if, for each closed point
$V_{q_1} \supseteq _{fe} V_{q_2}$
if, for each closed point
![]() $c_{2} \in V^{\mathrm {cl}}_{q_2}$
, there exists a closed point
$c_{2} \in V^{\mathrm {cl}}_{q_2}$
, there exists a closed point
![]() $c_{1} \in V^{\mathrm { cl}}_{q_{1}}$
, such that
$c_{1} \in V^{\mathrm { cl}}_{q_{1}}$
, such that
![]() $c_{1} \sim _{fe} c_{2}$
. Moreover, we denote by
$c_{1} \sim _{fe} c_{2}$
. Moreover, we denote by
![]() $V_{q_1} =_{fe} V_{q_2}$
if
$V_{q_1} =_{fe} V_{q_2}$
if
![]() $V_{q_1} \supseteq _{fe} V_{q_2}$
and
$V_{q_1} \supseteq _{fe} V_{q_2}$
and
![]() $V_{q_1} \subseteq _{fe} V_{q_2}$
. Moreover, we also denote by
$V_{q_1} \subseteq _{fe} V_{q_2}$
. Moreover, we also denote by
![]() $q_{1} \sim _{fe} q_{2}$
if
$q_{1} \sim _{fe} q_{2}$
if
![]() $V_{q_{1}}=_{fe} V_{q_{2}}$
.
$V_{q_{1}}=_{fe} V_{q_{2}}$
.
We have the following proposition.
Proposition 2.2. Let
![]() $\omega : M_{g, n}^{\mathrm {ord}} \rightarrow M_{g, n, \mathbb {F}_{p}}$
be the morphism induced by the natural morphism
$\omega : M_{g, n}^{\mathrm {ord}} \rightarrow M_{g, n, \mathbb {F}_{p}}$
be the morphism induced by the natural morphism
![]() $\mathcal {M}_{g, n}^{\mathrm {ord}} \rightarrow \mathcal {M}_{g, n, \mathbb {F}_{p}}$
. Let
$\mathcal {M}_{g, n}^{\mathrm {ord}} \rightarrow \mathcal {M}_{g, n, \mathbb {F}_{p}}$
. Let
![]() $i\in \{1,2\}$
, and let
$i\in \{1,2\}$
, and let
![]() $q_{i} \in M_{g, n}^{\mathrm {ord}}$
and
$q_{i} \in M_{g, n}^{\mathrm {ord}}$
and
![]() $q^{\prime }_{i} \stackrel {\mathrm {def}}{=} \omega (q_{i}) \in M_{g, n, \mathbb {F}_{p}}$
. Then we have
$q^{\prime }_{i} \stackrel {\mathrm {def}}{=} \omega (q_{i}) \in M_{g, n, \mathbb {F}_{p}}$
. Then we have
![]() $V_{q_{1}} \supseteq _{fe} V_{q_{2}}$
if and only if
$V_{q_{1}} \supseteq _{fe} V_{q_{2}}$
if and only if
![]() $V_{q^{\prime }_{1}} \supseteq V_{q^{\prime }_{2}}$
. In particular, we have
$V_{q^{\prime }_{1}} \supseteq V_{q^{\prime }_{2}}$
. In particular, we have
![]() $V_{q_{1}} =_{fe} V_{q_{2}}$
if and only if
$V_{q_{1}} =_{fe} V_{q_{2}}$
if and only if
![]() $V_{q^{\prime }_{1}} = V_{q^{\prime }_{2}}$
. Namely, we have
$V_{q^{\prime }_{1}} = V_{q^{\prime }_{2}}$
. Namely, we have
![]() $V_{q_{1}}=_{fe} V_{q_{2}}$
if and only if
$V_{q_{1}}=_{fe} V_{q_{2}}$
if and only if
![]() $U_{X_{q_{1}}} \cong U_{X_{q_{2}}}$
as schemes.
$U_{X_{q_{1}}} \cong U_{X_{q_{2}}}$
as schemes.
Proof. Suppose that
![]() $q_{i}$
,
$q_{i}$
,
![]() $i\in \{1, 2\}$
, is a closed point of
$i\in \{1, 2\}$
, is a closed point of
![]() $M_{g, n}^{\mathrm {ord}}$
. If
$M_{g, n}^{\mathrm {ord}}$
. If
![]() $V_{q_{1}} \supseteq _{fe} V_{q_{2}}$
, we see immediately
$V_{q_{1}} \supseteq _{fe} V_{q_{2}}$
, we see immediately
![]() $q_{1} \sim q_{2}$
. Thus, we obtain
$q_{1} \sim q_{2}$
. Thus, we obtain
![]() $U_{X_{q_{1}}} \cong U_{X_{q_{2}}}$
as schemes. This means
$U_{X_{q_{1}}} \cong U_{X_{q_{2}}}$
as schemes. This means
![]() $q^{\prime }_{1}=q^{\prime }_{2}$
. Conversely, if
$q^{\prime }_{1}=q^{\prime }_{2}$
. Conversely, if
![]() $V_{q^{\prime }_{1}} \supseteq V_{q^{\prime }_{2}}$
, then we have
$V_{q^{\prime }_{1}} \supseteq V_{q^{\prime }_{2}}$
, then we have
![]() $q^{\prime }_{1}=q^{\prime }_{2}$
. Thus, we obtain
$q^{\prime }_{1}=q^{\prime }_{2}$
. Thus, we obtain
![]() $q_{1}\sim q_{2}$
.
$q_{1}\sim q_{2}$
.
Suppose that
![]() $q_{i}$
,
$q_{i}$
,
![]() $i\in \{1, 2\}$
, is an arbitrary point of
$i\in \{1, 2\}$
, is an arbitrary point of
![]() $M_{g, n}^{\mathrm {ord}}$
. If
$M_{g, n}^{\mathrm {ord}}$
. If
![]() $V_{q_{1}} \supseteq _{fe} V_{q_{2}}$
, then the case of closed points implies
$V_{q_{1}} \supseteq _{fe} V_{q_{2}}$
, then the case of closed points implies
![]() $V_{q^{\prime }_{1}}^{\mathrm {cl}} \supseteq V_{q^{\prime }_{2}}^{\mathrm { cl}}.$
Since
$V_{q^{\prime }_{1}}^{\mathrm {cl}} \supseteq V_{q^{\prime }_{2}}^{\mathrm { cl}}.$
Since
![]() $V_{q^{\prime }_{1}}$
and
$V_{q^{\prime }_{1}}$
and
![]() $V_{q^{\prime }_{2}}$
are irreducible, we obtain
$V_{q^{\prime }_{2}}$
are irreducible, we obtain
![]() $V_{q^{\prime }_{1}} \supseteq V_{q^{\prime }_{2}}.$
Conversely, if
$V_{q^{\prime }_{1}} \supseteq V_{q^{\prime }_{2}}.$
Conversely, if
![]() $V_{q^{\prime }_{1}} \supseteq V_{q^{\prime }_{2}}$
, we note that
$V_{q^{\prime }_{1}} \supseteq V_{q^{\prime }_{2}}$
, we note that
![]() $V_{q_{i}}$
is an irreducible component of
$V_{q_{i}}$
is an irreducible component of
![]() $(\omega )^{-1}(V_{q^{\prime }_{i}})$
. Then the case of closed points implies
$(\omega )^{-1}(V_{q^{\prime }_{i}})$
. Then the case of closed points implies
![]() $V_{q_{1}} \supseteq _{fe} V_{q_{2}}$
.
$V_{q_{1}} \supseteq _{fe} V_{q_{2}}$
.
2.1.4.
Denote by
![]() $\mathrm {Hom}^{\mathrm {op}}_{\mathrm {pg}}(-,-)$
the set of open continuous homomorphisms of profinite groups, and by
$\mathrm {Hom}^{\mathrm {op}}_{\mathrm {pg}}(-,-)$
the set of open continuous homomorphisms of profinite groups, and by
![]() $\text {Isom}_{\mathrm {pg}}(-,-)$
the set of isomorphisms of profinite groups. We have the following conjecture.
$\text {Isom}_{\mathrm {pg}}(-,-)$
the set of isomorphisms of profinite groups. We have the following conjecture.
Weak Hom-version Conjecture. Let
![]() $q_{i} \in M_{g, n}$
(respectively,
$q_{i} \in M_{g, n}$
(respectively,
![]() $q_{i} \in M_{g, n, \mathbb {F}_{p}}$
),
$q_{i} \in M_{g, n, \mathbb {F}_{p}}$
),
![]() $i\in \{1, 2\}$
, be an arbitrary point. Then we have
$i\in \{1, 2\}$
, be an arbitrary point. Then we have
is nonempty if and only if
![]() $V_{q_{1}}\supseteq _{fe}V_{q_{2}}$
(respectively,
$V_{q_{1}}\supseteq _{fe}V_{q_{2}}$
(respectively,
![]() $V_{q_{1}}\supseteq V_{q_{2}}$
).
$V_{q_{1}}\supseteq V_{q_{2}}$
).
The Weak Hom-version Conjecture means that the topological structures of the moduli spaces of smooth pointed stable curves can be understood by the tame fundamental groups of curves. In particular, the Weak Hom-version Conjecture implies the following conjecture, which was essentially formulated by Tamagawa ([Reference TamagawaT3]).
Weak Isom-version Conjecture. Let
![]() $q_{i} \in M_{g, n}$
(respectively,
$q_{i} \in M_{g, n}$
(respectively,
![]() $q_{i} \in M_{g, n, \mathbb {F}_{p}}$
),
$q_{i} \in M_{g, n, \mathbb {F}_{p}}$
),
![]() $i\in \{1, 2\}$
, be an arbitrary point. Then we have
$i\in \{1, 2\}$
, be an arbitrary point. Then we have
is nonempty if and only if
![]() $V_{q_{1}}=_{fe}V_{q_{2}}$
(respectively,
$V_{q_{1}}=_{fe}V_{q_{2}}$
(respectively,
![]() $V_{q_{1}}=V_{q_{2}}$
).
$V_{q_{1}}=V_{q_{2}}$
).
The Weak Isom-version Conjecture means that the set structures of the moduli spaces of smooth pointed stable curves can be understood by the tame fundamental groups of curves.
2.2. The pointed collection conjecture
In this subsection, we formulate the second conjecture of the present paper, which we call “the pointed collection conjecture.”
2.2.1.
We maintain the notation introduced in Section 2.1.2.
2.2.2.
Let q be an arbitrary point of
![]() $M_{g, n}^{\mathrm {ord}}$
and
$M_{g, n}^{\mathrm {ord}}$
and
![]() $G \in \pi ^{\mathrm {t}}_{A}(q)$
an arbitrary finite group. We put
$G \in \pi ^{\mathrm {t}}_{A}(q)$
an arbitrary finite group. We put
Then we have the following result.
Proposition 2.3. Let q be an arbitrary point of
![]() $M_{g, n}^{\mathrm {ord}}$
and
$M_{g, n}^{\mathrm {ord}}$
and
![]() $G \in \pi ^{\mathrm {t}}_{A}(q)$
an arbitrary finite group. Then the set
$G \in \pi ^{\mathrm {t}}_{A}(q)$
an arbitrary finite group. Then the set
![]() $U_{G}$
contains an open neighborhood of q in
$U_{G}$
contains an open neighborhood of q in
![]() $M_{g, n}^{\mathrm {ord}}$
.
$M_{g, n}^{\mathrm {ord}}$
.
Proof. Proposition 2.3 was proved by Stevenson when
![]() $n=0$
and q is a closed point of
$n=0$
and q is a closed point of
![]() $M_{g, 0}$
(cf. [Reference StevensonSte, Proposition 4.2]). Moreover, by similar arguments to the arguments given in the proof of [Reference StevensonSte, Proposition 4.2], Proposition 2.3 also holds for
$M_{g, 0}$
(cf. [Reference StevensonSte, Proposition 4.2]). Moreover, by similar arguments to the arguments given in the proof of [Reference StevensonSte, Proposition 4.2], Proposition 2.3 also holds for
![]() $n\geq 0$
.
$n\geq 0$
.
Definition 2.4. We denote by
![]() $q_{\mathrm {gen}}$
the generic point of
$q_{\mathrm {gen}}$
the generic point of
![]() $M_{g, n}^{\mathrm {ord}}$
, and let
$M_{g, n}^{\mathrm {ord}}$
, and let
 $$ \begin{align*}\mathcal{C} \subseteq {\pi}_{A}^{\mathrm{t}}(q_{\mathrm{gen}})=\bigcup_{q \in M_{g, n}^{\mathrm{ord, cl}}}{\pi}_{A}^{\mathrm{t}}(q)\end{align*} $$
$$ \begin{align*}\mathcal{C} \subseteq {\pi}_{A}^{\mathrm{t}}(q_{\mathrm{gen}})=\bigcup_{q \in M_{g, n}^{\mathrm{ord, cl}}}{\pi}_{A}^{\mathrm{t}}(q)\end{align*} $$
be a subset of
![]() ${\pi }_{A}^{\mathrm {t}}(q_{\mathrm {gen}})$
. We shall say that
${\pi }_{A}^{\mathrm {t}}(q_{\mathrm {gen}})$
. We shall say that
![]() $\mathcal {C}$
is a pointed collection if the following conditions are satisfied:
$\mathcal {C}$
is a pointed collection if the following conditions are satisfied:
-
(i)
 $0<\#((\bigcap _{G\in \mathcal {C}}U_{G}) \cap M_{g, n}^{\mathrm {ord, cl}}) < \infty $
;
$0<\#((\bigcap _{G\in \mathcal {C}}U_{G}) \cap M_{g, n}^{\mathrm {ord, cl}}) < \infty $
; -
(ii)
 $U_{G'} \cap (\bigcap _{G\in \mathcal {C}}U_{G})\cap M_{g, n}^{\mathrm {ord, cl}} =\emptyset $
for each
$U_{G'} \cap (\bigcap _{G\in \mathcal {C}}U_{G})\cap M_{g, n}^{\mathrm {ord, cl}} =\emptyset $
for each
 $G' \in {\pi }_{A}^{\mathrm {t}}(q_{\mathrm {gen}})$
, such that
$G' \in {\pi }_{A}^{\mathrm {t}}(q_{\mathrm {gen}})$
, such that
 $G' \not \in \mathcal {C}$
.
$G' \not \in \mathcal {C}$
.
On the other hand, for each closed point
![]() $t \in M_{g, n}^{\mathrm {ord, cl}}$
, we may define a set associated to t as follows:
$t \in M_{g, n}^{\mathrm {ord, cl}}$
, we may define a set associated to t as follows:
Note that, if
![]() $t \in V^{\mathrm {cl}}_{q}$
and q is not a closed point, then a result of Tamagawa ([Reference TamagawaT5, Theorem 0.3]) implies that
$t \in V^{\mathrm {cl}}_{q}$
and q is not a closed point, then a result of Tamagawa ([Reference TamagawaT5, Theorem 0.3]) implies that
![]() $\mathcal {C}_{t} \subseteq {\pi }_{A}^{\mathrm {t}}(q)$
and
$\mathcal {C}_{t} \subseteq {\pi }_{A}^{\mathrm {t}}(q)$
and
![]() $\mathcal {C}_{t} \neq {\pi }_{A}^{\mathrm {t}}(q)$
. Moreover, we denote by
$\mathcal {C}_{t} \neq {\pi }_{A}^{\mathrm {t}}(q)$
. Moreover, we denote by
2.2.3.
At present, no published results are known concerning the Weak Hom-version conjecture (or the Weak Isom-version Conjecture) for nonclosed points. The main difficulty of proving the Weak Hom-version Conjecture (or the weak Isom-version conjecture) for nonclosed points of
![]() $M_{g, n}^{\mathrm {ord}}$
is the following: For each
$M_{g, n}^{\mathrm {ord}}$
is the following: For each
![]() $q \in M_{g, n}^{\mathrm {ord}}$
, we do not know how to reconstruct the tame fundamental groups of closed points of
$q \in M_{g, n}^{\mathrm {ord}}$
, we do not know how to reconstruct the tame fundamental groups of closed points of
![]() $V_{q}$
group-theoretically from
$V_{q}$
group-theoretically from
![]() ${\pi }_{1}^{\mathrm {t}}(q)$
.
${\pi }_{1}^{\mathrm {t}}(q)$
.
Once the tame fundamental groups of the closed points of
![]() $V_q$
can be reconstructed group-theoretically from
$V_q$
can be reconstructed group-theoretically from
![]() ${\pi }_{1}^{\mathrm {t}}(q)$
, then the weak Hom-version conjecture for closed points of
${\pi }_{1}^{\mathrm {t}}(q)$
, then the weak Hom-version conjecture for closed points of
![]() $M_{g, n}^{\mathrm {ord}}$
implies that the set of closed points of
$M_{g, n}^{\mathrm {ord}}$
implies that the set of closed points of
![]() $V_{q}$
can be reconstructed group-theoretically from
$V_{q}$
can be reconstructed group-theoretically from
![]() ${\pi }_{1}^{\mathrm {t}}(q)$
. Thus, the Weak Hom-version Conjecture for nonclosed points of
${\pi }_{1}^{\mathrm {t}}(q)$
. Thus, the Weak Hom-version Conjecture for nonclosed points of
![]() $M_{g, n}^{\mathrm {ord}}$
can be deduced from the Weak Hom-version Conjecture for closed points of
$M_{g, n}^{\mathrm {ord}}$
can be deduced from the Weak Hom-version Conjecture for closed points of
![]() $M_{g, n}^{\mathrm {ord}}$
.
$M_{g, n}^{\mathrm {ord}}$
.
Let
![]() $q \in M_{g, n}^{\mathrm {ord}}$
. Since the isomorphism class of
$q \in M_{g, n}^{\mathrm {ord}}$
. Since the isomorphism class of
![]() ${\pi }_{1}^{\mathrm {t}}(q)$
as a profinite group can be determined by the set
${\pi }_{1}^{\mathrm {t}}(q)$
as a profinite group can be determined by the set
![]() ${\pi }_{A}^{\mathrm {t}}(q)$
, the following conjecture tells us how to reconstruct group-theoretically the set of finite quotients of a closed point of
${\pi }_{A}^{\mathrm {t}}(q)$
, the following conjecture tells us how to reconstruct group-theoretically the set of finite quotients of a closed point of
![]() $V_{q}$
from
$V_{q}$
from
![]() ${\pi }_{A}^{\mathrm {t}}(q)$
(or
${\pi }_{A}^{\mathrm {t}}(q)$
(or
![]() ${\pi }_{1}^{\mathrm {t}}(q)$
).
${\pi }_{1}^{\mathrm {t}}(q)$
).
Pointed Collection Conjecture. For each
![]() $t \in M_{g, n}^{\mathrm {ord, cl}}$
, the set
$t \in M_{g, n}^{\mathrm {ord, cl}}$
, the set
![]() $\mathcal {C}_{t}$
associated to t is a pointed collection. Moreover, let
$\mathcal {C}_{t}$
associated to t is a pointed collection. Moreover, let
![]() $q\in M_{g, n}^{\mathrm {ord}}$
. Then the natural map
$q\in M_{g, n}^{\mathrm {ord}}$
. Then the natural map
is a bijection, where
![]() $[t]$
denotes the image of t in
$[t]$
denotes the image of t in
![]() $\mathscr {V}_{q}^{\mathrm {cl}}\stackrel {\mathrm {def}}{=} V_{q}^{\mathrm {cl}}/\sim _{fe}$
.
$\mathscr {V}_{q}^{\mathrm {cl}}\stackrel {\mathrm {def}}{=} V_{q}^{\mathrm {cl}}/\sim _{fe}$
.
Write
![]() $q'\in M_{g, n, \mathbb {F}_{p}}$
for the image
$q'\in M_{g, n, \mathbb {F}_{p}}$
for the image
![]() $\omega (q) $
. Then we have
$\omega (q) $
. Then we have
![]() $\mathscr {V}^{\mathrm {cl}}_{q}=V_{q'}^{\mathrm {cl}}$
. This means that the pointed collection conjecture holds if and only if the Weak Hom-version Conjecture holds.
$\mathscr {V}^{\mathrm {cl}}_{q}=V_{q'}^{\mathrm {cl}}$
. This means that the pointed collection conjecture holds if and only if the Weak Hom-version Conjecture holds.
3. Reconstructions of marked points
3.1. Anabelian reconstructions
3.1.1. Settings
We maintain the notation introduced in Section 2.1.1.
3.1.2.
Let us recall the definitions concerning “anabelian reconstructions.”
Definition 3.1. Let
![]() $\mathcal {F}$
be a geometric object and
$\mathcal {F}$
be a geometric object and
![]() $\Pi _{\mathcal {F}}$
a profinite group associated to the object
$\Pi _{\mathcal {F}}$
a profinite group associated to the object
![]() $\mathcal {F}$
. Suppose that we are given an invariant
$\mathcal {F}$
. Suppose that we are given an invariant
![]() $\text {Inv}_{\mathcal {F} }$
depending on the isomorphism class of
$\text {Inv}_{\mathcal {F} }$
depending on the isomorphism class of
![]() $\mathcal {F}$
(in a certain category), and that we are given an additional structure
$\mathcal {F}$
(in a certain category), and that we are given an additional structure
![]() $\text {Add}_{\mathcal {F}}$
(e.g., a family of subgroups, a family of quotient groups) on the profinite group
$\text {Add}_{\mathcal {F}}$
(e.g., a family of subgroups, a family of quotient groups) on the profinite group
![]() $\Pi _{\mathcal {F}}$
depending functorially on
$\Pi _{\mathcal {F}}$
depending functorially on
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
We shall say that
![]() $\text {Inv}_{\mathcal {F}}$
can be mono-anabelian reconstructed from
$\text {Inv}_{\mathcal {F}}$
can be mono-anabelian reconstructed from
![]() $\Pi _{\mathcal {F}}$
if there exists a group-theoretical algorithm whose input datum is
$\Pi _{\mathcal {F}}$
if there exists a group-theoretical algorithm whose input datum is
![]() $\Pi _{\mathcal {F}}$
, and whose output datum is
$\Pi _{\mathcal {F}}$
, and whose output datum is
![]() $\text {Inv}_{\mathcal {F}}$
. We shall say that
$\text {Inv}_{\mathcal {F}}$
. We shall say that
![]() $\text {Add}_{\mathcal {F}}$
can be mono-anabelian reconstructed from
$\text {Add}_{\mathcal {F}}$
can be mono-anabelian reconstructed from
![]() $\Pi _{\mathcal {F}}$
if there exists a group-theoretical algorithm whose input datum is
$\Pi _{\mathcal {F}}$
if there exists a group-theoretical algorithm whose input datum is
![]() $\Pi _{\mathcal {F}}$
, and whose output datum is
$\Pi _{\mathcal {F}}$
, and whose output datum is
![]() $\text {Add}_{\mathcal {F}}$
.
$\text {Add}_{\mathcal {F}}$
.
Let
![]() $\mathcal {F}_{i},\ i \in \{1, 2\},$
be a geometric object and
$\mathcal {F}_{i},\ i \in \{1, 2\},$
be a geometric object and
![]() $\Pi _{\mathcal {F}_{i}}$
a profinite group associated to the geometric object
$\Pi _{\mathcal {F}_{i}}$
a profinite group associated to the geometric object
![]() $\mathcal {F}_{i}$
. Suppose that we are given an additional structure
$\mathcal {F}_{i}$
. Suppose that we are given an additional structure
![]() $\text {Add}_{\mathcal {F}_{i}}$
on the profinite group
$\text {Add}_{\mathcal {F}_{i}}$
on the profinite group
![]() $\Pi _{\mathcal {F}_{i}}$
, depending functorially on
$\Pi _{\mathcal {F}_{i}}$
, depending functorially on
![]() $\mathcal {F}_{i}$
. We shall say that a map (or a morphism)
$\mathcal {F}_{i}$
. We shall say that a map (or a morphism)
![]() $\text {Add}_{\mathcal {F}_{1}} \rightarrow \text {Add}_{\mathcal {F}_{2}}$
can be mono-anabelian reconstructed from an open continuous homomorphism
$\text {Add}_{\mathcal {F}_{1}} \rightarrow \text {Add}_{\mathcal {F}_{2}}$
can be mono-anabelian reconstructed from an open continuous homomorphism
![]() $\Pi _{\mathcal {F}_{1}} \rightarrow \Pi _{\mathcal {F}_{2}}$
if there exists a group-theoretical algorithm whose input datum is
$\Pi _{\mathcal {F}_{1}} \rightarrow \Pi _{\mathcal {F}_{2}}$
if there exists a group-theoretical algorithm whose input datum is
![]() $\Pi _{\mathcal {F}_{1}} \rightarrow \Pi _{\mathcal {F}_{2}}$
, and whose output datum is
$\Pi _{\mathcal {F}_{1}} \rightarrow \Pi _{\mathcal {F}_{2}}$
, and whose output datum is
![]() $\text {Add}_{\mathcal {F}_{1}} \rightarrow \text {Add}_{\mathcal {F}_{2}}$
.
$\text {Add}_{\mathcal {F}_{1}} \rightarrow \text {Add}_{\mathcal {F}_{2}}$
.
3.1.3.
Let K be the function field of X, and let
![]() $\widetilde K$
be the maximal Galois extension of K in a fixed separable closure of K, unramified over
$\widetilde K$
be the maximal Galois extension of K in a fixed separable closure of K, unramified over
![]() $U_{X}$
and at most tamely ramified over
$U_{X}$
and at most tamely ramified over
![]() $D_{X}$
. Then we may identify
$D_{X}$
. Then we may identify
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
with
${\pi }_{1}^{\mathrm {t}}(U_{X})$
with
![]() $\text {Gal}(\widetilde K/K)$
. We define the universal tame covering of
$\text {Gal}(\widetilde K/K)$
. We define the universal tame covering of
![]() $(X, D_{X})$
associated to
$(X, D_{X})$
associated to
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
to be
${\pi }_{1}^{\mathrm {t}}(U_{X})$
to be
where
![]() $\widetilde X$
denotes the normalization of X in
$\widetilde X$
denotes the normalization of X in
![]() $\widetilde K$
, and
$\widetilde K$
, and
![]() $D_{\widetilde X}$
denotes the inverse image of
$D_{\widetilde X}$
denotes the inverse image of
![]() $D_{X}$
in
$D_{X}$
in
![]() $\widetilde X$
. Then there is a natural action of
$\widetilde X$
. Then there is a natural action of
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
on
${\pi }_{1}^{\mathrm {t}}(U_{X})$
on
![]() $(\widetilde X, D_{\widetilde X})$
. For each
$(\widetilde X, D_{\widetilde X})$
. For each
![]() $\widetilde e \in D_{\widetilde X}$
, we denote by
$\widetilde e \in D_{\widetilde X}$
, we denote by
![]() $I_{\widetilde e}$
the inertia subgroup of
$I_{\widetilde e}$
the inertia subgroup of
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
associated to
${\pi }_{1}^{\mathrm {t}}(U_{X})$
associated to
![]() $\widetilde e$
(i.e., the stabilizer of
$\widetilde e$
(i.e., the stabilizer of
![]() $\widetilde e$
in
$\widetilde e$
in
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
). Then we have
${\pi }_{1}^{\mathrm {t}}(U_{X})$
). Then we have
![]() $I_{\widetilde e} \cong \widehat {\mathbb {Z}}(1)^{p'}$
, where
$I_{\widetilde e} \cong \widehat {\mathbb {Z}}(1)^{p'}$
, where
![]() $\widehat {\mathbb {Z}}(1)^{p'}$
denotes the prime-to-p part of
$\widehat {\mathbb {Z}}(1)^{p'}$
denotes the prime-to-p part of
![]() $\widehat {\mathbb {Z}}(1)$
. The following result was proved by Tamagawa ([Reference TamagawaT4, Lemma 5.1 and Theorem 5.2]).
$\widehat {\mathbb {Z}}(1)$
. The following result was proved by Tamagawa ([Reference TamagawaT4, Lemma 5.1 and Theorem 5.2]).
Proposition 3.2.
(i) The type
![]() $(g_{X}, n_{X})$
can be mono-anabelian reconstructed from
$(g_{X}, n_{X})$
can be mono-anabelian reconstructed from
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
.
${\pi }_{1}^{\mathrm {t}}(U_{X})$
.
(ii) Let
![]() $\widetilde e$
and
$\widetilde e$
and
![]() $\widetilde e'$
be two points of
$\widetilde e'$
be two points of
![]() $D_{\widetilde X}$
distinct from each other. Then the intersection of
$D_{\widetilde X}$
distinct from each other. Then the intersection of
![]() $I_{\widetilde e}$
and
$I_{\widetilde e}$
and
![]() $I_{\widetilde e'}$
is trivial in
$I_{\widetilde e'}$
is trivial in
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
. Moreover, the map
${\pi }_{1}^{\mathrm {t}}(U_{X})$
. Moreover, the map
is an injection, where
![]() $\mathrm {Sub}(-)$
denotes the set of closed subgroups of
$\mathrm {Sub}(-)$
denotes the set of closed subgroups of
![]() $(-)$
.
$(-)$
.
(iii) Write
![]() $\mathrm {Ine}({\pi }_{1}^{\mathrm {t}}(U_{X}))$
for the set of inertia subgroups in
$\mathrm {Ine}({\pi }_{1}^{\mathrm {t}}(U_{X}))$
for the set of inertia subgroups in
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
, namely, the image of the map
${\pi }_{1}^{\mathrm {t}}(U_{X})$
, namely, the image of the map
![]() $D_{\widetilde X} \rightarrow \mathrm {Sub}({\pi }_{1}^{\mathrm {t}}(U_{X}))$
. Then
$D_{\widetilde X} \rightarrow \mathrm {Sub}({\pi }_{1}^{\mathrm {t}}(U_{X}))$
. Then
![]() $\mathrm {Ine}({\pi }_{1}^{\mathrm {t}}(U_{X}))$
can be mono-anabelian reconstructed from
$\mathrm {Ine}({\pi }_{1}^{\mathrm {t}}(U_{X}))$
can be mono-anabelian reconstructed from
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
. In particular, the set of marked points
${\pi }_{1}^{\mathrm {t}}(U_{X})$
. In particular, the set of marked points
![]() $D_{X}$
and
$D_{X}$
and
![]() ${\pi }_{1}(X)$
can be mono-anabelian reconstructed from
${\pi }_{1}(X)$
can be mono-anabelian reconstructed from
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
.
${\pi }_{1}^{\mathrm {t}}(U_{X})$
.
The main purposes of the remainder of the present section are as follows: We will give a new mono-anabelian reconstruction of
![]() $\mathrm {Ine}({\pi }_{1}^{\mathrm {t}}(U_{X}))$
, and prove that the mono-anabelian reconstruction (i.e., the group-theoretical algorithm) is compatible with any open continuous homomorphisms of tame fundamental groups of smooth pointed stable curves with a fixed type.
$\mathrm {Ine}({\pi }_{1}^{\mathrm {t}}(U_{X}))$
, and prove that the mono-anabelian reconstruction (i.e., the group-theoretical algorithm) is compatible with any open continuous homomorphisms of tame fundamental groups of smooth pointed stable curves with a fixed type.
3.2. The set of marked points
3.2.1. Settings
We maintain the notation introduced in Section 2.1.1. Moreover, we suppose that
![]() $g_{X} \geq 2$
and
$g_{X} \geq 2$
and
![]() $n_{X}>0$
.
$n_{X}>0$
.
3.2.2.
In this subsection, we will prove that the set of marked points can be regarded as a quotient set of a set of cohomological classes of a suitable covering of curves (i.e., Proposition 3.3). The main idea is the following: By taking a suitable étale covering with a prime degree
![]() $f: (Y, D_{Y}) \rightarrow (X, D_{X})$
, for every marked point
$f: (Y, D_{Y}) \rightarrow (X, D_{X})$
, for every marked point
![]() $x \in D_{X}$
, there exists a set of tame coverings with a prime degree which is totally ramified over the inverse image
$x \in D_{X}$
, there exists a set of tame coverings with a prime degree which is totally ramified over the inverse image
![]() $f^{-1}(x)$
. Then x can be regarded as the set of cohomological classes corresponding to such coverings.
$f^{-1}(x)$
. Then x can be regarded as the set of cohomological classes corresponding to such coverings.
3.2.3.
Let
![]() $h: (W, D_{W}) \rightarrow (X, D_{X})$
be a connected Galois tame covering over k. We put
$h: (W, D_{W}) \rightarrow (X, D_{X})$
be a connected Galois tame covering over k. We put
Let
![]() $(Y, D_{Y})$
be a smooth pointed stable curve over k. We shall say that
$(Y, D_{Y})$
be a smooth pointed stable curve over k. We shall say that
is an mp-triple associated to
![]() $(X, D_{X})$
if the following conditions hold: (i)
$(X, D_{X})$
if the following conditions hold: (i)
![]() $\ell $
and d are prime numbers distinct from each other, such that
$\ell $
and d are prime numbers distinct from each other, such that
![]() $(\ell , p)=(d, p)=1$
and
$(\ell , p)=(d, p)=1$
and
![]() $\ell \equiv 1 \ (\text {mod}\ d)$
; then all dth roots of unity are contained in
$\ell \equiv 1 \ (\text {mod}\ d)$
; then all dth roots of unity are contained in
![]() $\mathbb {F}_{\ell }$
; (ii) f is a Galois étale covering over k whose Galois group is isomorphic to
$\mathbb {F}_{\ell }$
; (ii) f is a Galois étale covering over k whose Galois group is isomorphic to
![]() $\mu _{d}$
, where
$\mu _{d}$
, where
![]() $\mu _{d} \subseteq \mathbb {F}_{\ell }^{\times }$
denotes the subgroup of dth roots of unity. Here, “mp” means “marked points.”
$\mu _{d} \subseteq \mathbb {F}_{\ell }^{\times }$
denotes the subgroup of dth roots of unity. Here, “mp” means “marked points.”
Then we have a natural injection
![]() $H^{1}_{\text {'et}}(Y, \mathbb {F}_{\ell })\hookrightarrow H^{1}_{\text {'et}}(U_Y, \mathbb {F}_{\ell })$
induced by the natural surjection
$H^{1}_{\text {'et}}(Y, \mathbb {F}_{\ell })\hookrightarrow H^{1}_{\text {'et}}(U_Y, \mathbb {F}_{\ell })$
induced by the natural surjection
![]() ${\pi }_{1}^{\mathrm {t}}(U_Y) \twoheadrightarrow {\pi }_{1}(Y)$
. Note that every nonzero element of
${\pi }_{1}^{\mathrm {t}}(U_Y) \twoheadrightarrow {\pi }_{1}(Y)$
. Note that every nonzero element of
![]() $H^{1}_{\text {'et}}(U_Y, \mathbb {F}_{\ell })$
induces a connected Galois tame covering of
$H^{1}_{\text {'et}}(U_Y, \mathbb {F}_{\ell })$
induces a connected Galois tame covering of
![]() $(Y, D_{Y})$
of degree
$(Y, D_{Y})$
of degree
![]() $\ell $
. We obtain an exact sequence
$\ell $
. We obtain an exact sequence
with a natural action of
![]() $\mu _{d}$
.
$\mu _{d}$
.
3.2.4.
Let
![]() $(\text {Div}^{0}_{D_{Y}}(Y)\otimes \mathbb {F}_{\ell })_{\mu _{d}} \subseteq \text {Div}^{0}_{D_{Y}}(Y)\otimes \mathbb {F}_{\ell }$
be the subset of elements on which
$(\text {Div}^{0}_{D_{Y}}(Y)\otimes \mathbb {F}_{\ell })_{\mu _{d}} \subseteq \text {Div}^{0}_{D_{Y}}(Y)\otimes \mathbb {F}_{\ell }$
be the subset of elements on which
![]() $\mu _{d}$
acts via the character
$\mu _{d}$
acts via the character
![]() $\mu _{d} \hookrightarrow \mathbb {F}_{\ell }^{\times }$
and
$\mu _{d} \hookrightarrow \mathbb {F}_{\ell }^{\times }$
and
![]() $M^{*}_{Y} \subseteq H^{1}_{\text {'et}}(U_Y, \mathbb {F}_{\ell })$
the subset of elements whose images are nonzero elements of
$M^{*}_{Y} \subseteq H^{1}_{\text {'et}}(U_Y, \mathbb {F}_{\ell })$
the subset of elements whose images are nonzero elements of
![]() $(\text {Div}^{0}_{D_{Y}}(Y)\otimes \mathbb {F}_{\ell })_{\mu _{d}}$
. For each
$(\text {Div}^{0}_{D_{Y}}(Y)\otimes \mathbb {F}_{\ell })_{\mu _{d}}$
. For each
![]() $\alpha \in M^{*}_{Y}$
, write
$\alpha \in M^{*}_{Y}$
, write
![]() $g_{\alpha }: (Y_{\alpha }, D_{Y_{\alpha }}) \rightarrow (Y, D_{Y})$
for the tame covering induced by
$g_{\alpha }: (Y_{\alpha }, D_{Y_{\alpha }}) \rightarrow (Y, D_{Y})$
for the tame covering induced by
![]() $\alpha $
. We define
$\alpha $
. We define
![]() $\epsilon : M_{Y}^{*} \rightarrow \mathbb {Z}$
, where
$\epsilon : M_{Y}^{*} \rightarrow \mathbb {Z}$
, where
![]() $ \epsilon (\alpha )\stackrel {\mathrm {def}}{=} \#D_{Y_{\alpha }}$
. Denote by
$ \epsilon (\alpha )\stackrel {\mathrm {def}}{=} \#D_{Y_{\alpha }}$
. Denote by
Note that since
![]() $(\ell , p)=(d, p)=1$
and
$(\ell , p)=(d, p)=1$
and
![]() $\#(f^{-1}(x))=\ell $
for all
$\#(f^{-1}(x))=\ell $
for all
![]() $x\in D_{X}$
, the structure of the maximal pro-prime-to-p quotient of
$x\in D_{X}$
, the structure of the maximal pro-prime-to-p quotient of
![]() ${\pi }_{1}^{\mathrm {t}}(U_{Y})$
(i.e., it’s isomorphic to the pro-prime-to-p completion of the topological fundamental group of a Riemann surface of type
${\pi }_{1}^{\mathrm {t}}(U_{Y})$
(i.e., it’s isomorphic to the pro-prime-to-p completion of the topological fundamental group of a Riemann surface of type
![]() $(g_{Y}, n_{Y})$
) implies that
$(g_{Y}, n_{Y})$
) implies that
![]() $M_{Y}$
is not empty.
$M_{Y}$
is not empty.
For each
![]() $\alpha \in M_{Y}$
, since the image of
$\alpha \in M_{Y}$
, since the image of
![]() $\alpha $
is contained in
$\alpha $
is contained in
![]() $(\text {Div}^{0}_{D_{Y}}(Y)\otimes \mathbb {F}_{\ell })_{\mu _{d}}$
, we obtain that the action of
$(\text {Div}^{0}_{D_{Y}}(Y)\otimes \mathbb {F}_{\ell })_{\mu _{d}}$
, we obtain that the action of
![]() $\mu _{d}$
on
$\mu _{d}$
on
![]() $\text {Ram}_{g_{\alpha }} \subseteq D_{Y}$
is transitive. Thus, there exists a unique marked point
$\text {Ram}_{g_{\alpha }} \subseteq D_{Y}$
is transitive. Thus, there exists a unique marked point
![]() $e_{\alpha } \in D_{X}$
, such that
$e_{\alpha } \in D_{X}$
, such that
![]() $f(y)=e_{\alpha }$
for each
$f(y)=e_{\alpha }$
for each
![]() $y \in \text {Ram}_{g_{\alpha }}$
.
$y \in \text {Ram}_{g_{\alpha }}$
.
For each
![]() $e \in D_{X}$
, we put
$e \in D_{X}$
, we put
Then, for any marked points
![]() $e, e' \in D_{X}$
distinct from each other, we have
$e, e' \in D_{X}$
distinct from each other, we have
![]() $M_{Y, e} \cap M_{Y, e'}=\emptyset $
and the disjoint union
$M_{Y, e} \cap M_{Y, e'}=\emptyset $
and the disjoint union
3.2.5.
Next, we define a preequivalence relation
![]() $\sim $
on
$\sim $
on
![]() $M_{Y}$
as follows: Let
$M_{Y}$
as follows: Let
![]() $\alpha , \beta \in M_{Y}$
. Then
$\alpha , \beta \in M_{Y}$
. Then
![]() $\alpha \sim \beta $
if
$\alpha \sim \beta $
if
![]() $\lambda \alpha +\mu \beta \in M_{Y}$
for each
$\lambda \alpha +\mu \beta \in M_{Y}$
for each
![]() $\lambda , \mu \in \mathbb {F}^{\times }_{\ell }$
for which
$\lambda , \mu \in \mathbb {F}^{\times }_{\ell }$
for which
![]() $\lambda \alpha +\mu \beta \in M_{Y}^{*}$
. Then we have the following proposition.
$\lambda \alpha +\mu \beta \in M_{Y}^{*}$
. Then we have the following proposition.
Proposition 3.3. The preequivalence relation
![]() $\sim $
on
$\sim $
on
![]() $M_{Y}$
is an equivalence relation. Moreover, the map
$M_{Y}$
is an equivalence relation. Moreover, the map
is a bijection, where
![]() $[\alpha ]$
denotes the image of
$[\alpha ]$
denotes the image of
![]() $\alpha $
in
$\alpha $
in
![]() $M_{Y}/\sim $
.
$M_{Y}/\sim $
.
Proof. Let
![]() $\beta , \gamma \in M_{Y}.$
If
$\beta , \gamma \in M_{Y}.$
If
![]() $\text {Ram}_{g_{\beta }}=\text {Ram}_{g_{\gamma }}$
, then, for each
$\text {Ram}_{g_{\beta }}=\text {Ram}_{g_{\gamma }}$
, then, for each
![]() $\lambda , \mu \in \mathbb {F}_{\ell }^{\times }$
for which
$\lambda , \mu \in \mathbb {F}_{\ell }^{\times }$
for which
![]() $\lambda \beta +\mu \gamma \neq 0$
, we have
$\lambda \beta +\mu \gamma \neq 0$
, we have
![]() $\text {Ram}_{g_{\lambda \beta +\mu \gamma }}=\text {Ram}_{g_{\beta }}=\text {Ram}_{g_{\gamma }}.$
Thus, we obtain that
$\text {Ram}_{g_{\lambda \beta +\mu \gamma }}=\text {Ram}_{g_{\beta }}=\text {Ram}_{g_{\gamma }}.$
Thus, we obtain that
![]() $\beta \sim \gamma $
. On the other hand, if
$\beta \sim \gamma $
. On the other hand, if
![]() $\beta \sim \gamma $
, we have
$\beta \sim \gamma $
, we have
![]() $\text {Ram}_{g_{\beta }}=\text {Ram}_{g_{\gamma }}$
. Otherwise, we have
$\text {Ram}_{g_{\beta }}=\text {Ram}_{g_{\gamma }}$
. Otherwise, we have
![]() $\#\text {Ram}_{g_{\beta +\gamma }}=2d$
. This means that
$\#\text {Ram}_{g_{\beta +\gamma }}=2d$
. This means that
![]() $\beta \sim \gamma \ \text {if and only if} \ \text {Ram}_{g_{\beta }}=\text {Ram}_{g_{\gamma }}.$
Then
$\beta \sim \gamma \ \text {if and only if} \ \text {Ram}_{g_{\beta }}=\text {Ram}_{g_{\gamma }}.$
Then
![]() $\sim $
is an equivalence relation on
$\sim $
is an equivalence relation on
![]() $M_{Y}\kern-1pt$
.
$M_{Y}\kern-1pt$
.
Let us prove that
![]() ${\vartheta }_{X}$
is a bijection. It is easy to see that
${\vartheta }_{X}$
is a bijection. It is easy to see that
![]() ${\vartheta }_{X}$
is an injection. On the other hand, for each
${\vartheta }_{X}$
is an injection. On the other hand, for each
![]() $e \in D_{X}$
, the structure of the maximal pro-
$e \in D_{X}$
, the structure of the maximal pro-
![]() $\ell $
tame fundamental groups implies that we may construct a connected tame Galois covering of
$\ell $
tame fundamental groups implies that we may construct a connected tame Galois covering of
![]() $h: (Z, D_{Z}) \rightarrow (Y, D_{Y})$
, such that h is totally tamely ramified over
$h: (Z, D_{Z}) \rightarrow (Y, D_{Y})$
, such that h is totally tamely ramified over
![]() $f^{-1}(e)$
(i.e., the element of
$f^{-1}(e)$
(i.e., the element of
![]() $H^{1}_{\text {'et}}(U_Y, \mathbb {F}_{\ell })$
induced by h is contained in
$H^{1}_{\text {'et}}(U_Y, \mathbb {F}_{\ell })$
induced by h is contained in
![]() $M_{Y}$
). Then
$M_{Y}$
). Then
![]() ${\vartheta }_{X}$
is a surjection. This completes the proof of Proposition 3.3.
${\vartheta }_{X}$
is a surjection. This completes the proof of Proposition 3.3.
Remark 3.3.1. We claim that the set
![]() $M_{Y}/\sim $
does not depend on the choices of mp-triples associated to
$M_{Y}/\sim $
does not depend on the choices of mp-triples associated to
![]() $(X, D_{X})$
. Let
$(X, D_{X})$
. Let
be an arbitrary mp-triple associated to
![]() $(X, D_{X})$
. Hence, we obtain a resulting set
$(X, D_{X})$
. Hence, we obtain a resulting set
![]() $M_{Y^{*}}/\sim $
and a natural bijection,
$M_{Y^{*}}/\sim $
and a natural bijection,
![]() ${\vartheta }_{X}^{*}: M_{Y^{*}}/\sim \rightarrow D_{X}.$
We will prove that there exists a natural bijection
${\vartheta }_{X}^{*}: M_{Y^{*}}/\sim \rightarrow D_{X}.$
We will prove that there exists a natural bijection
![]() $\delta : M_{Y^{*}}/\sim \stackrel {\sim }{\rightarrow } M_{Y}/\sim $
, such that
$\delta : M_{Y^{*}}/\sim \stackrel {\sim }{\rightarrow } M_{Y}/\sim $
, such that
![]() ${\vartheta }_{X}^{*}={\vartheta }_{X}\circ \delta $
.
${\vartheta }_{X}^{*}={\vartheta }_{X}\circ \delta $
.
First, suppose that
![]() $\ell \neq \ell ^{*}$
and
$\ell \neq \ell ^{*}$
and
![]() $d\neq d^{*}$
. Then we may construct a natural bijection
$d\neq d^{*}$
. Then we may construct a natural bijection
![]() $\delta : M_{Y^{*}}/\sim \stackrel {\sim }{\rightarrow } M_{Y}/\sim $
as follows. Let
$\delta : M_{Y^{*}}/\sim \stackrel {\sim }{\rightarrow } M_{Y}/\sim $
as follows. Let
![]() $\alpha \in M_{Y}$
and
$\alpha \in M_{Y}$
and
![]() $\alpha ^{*}\in M_{Y^{*}}$
. Write
$\alpha ^{*}\in M_{Y^{*}}$
. Write
![]() $(Y_{\alpha }, D_{Y_{\alpha }}) \rightarrow (Y, D_{Y})$
and
$(Y_{\alpha }, D_{Y_{\alpha }}) \rightarrow (Y, D_{Y})$
and
![]() $(Y_{\alpha ^{*}}, D_{Y_{\alpha ^{*}}}) \rightarrow (Y^{*}, D_{Y^{*}})$
for the Galois tame coverings induced by
$(Y_{\alpha ^{*}}, D_{Y_{\alpha ^{*}}}) \rightarrow (Y^{*}, D_{Y^{*}})$
for the Galois tame coverings induced by
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha ^{*}$
, respectively. We consider the following fiber product in the category of smooth pointed stable curves
$\alpha ^{*}$
, respectively. We consider the following fiber product in the category of smooth pointed stable curves
which is a smooth pointed stable curve over k. Thus, we obtain a connected tame covering
![]() $(Y_{\alpha }, D_{Y_{\alpha }})\times _{(X, D_{X})} (Y_{\alpha ^{*}}, D_{Y_{\alpha ^{*}}}) \rightarrow (X, D_{X})$
of degree
$(Y_{\alpha }, D_{Y_{\alpha }})\times _{(X, D_{X})} (Y_{\alpha ^{*}}, D_{Y_{\alpha ^{*}}}) \rightarrow (X, D_{X})$
of degree
![]() $dd^{*}\ell \ell ^{*}$
. Then it is easy to check that
$dd^{*}\ell \ell ^{*}$
. Then it is easy to check that
![]() ${\vartheta }_{X}([\alpha ])={\vartheta }_{X}^{*}([\alpha ^{*}])$
if and only if the cardinality of the set of marked points of
${\vartheta }_{X}([\alpha ])={\vartheta }_{X}^{*}([\alpha ^{*}])$
if and only if the cardinality of the set of marked points of
![]() $(Y_{\alpha }, D_{Y_{\alpha }})\times _{(X, D_{X})} (Y_{\alpha ^{*}}, D_{Y_{\alpha ^{*}}})$
is equal to
$(Y_{\alpha }, D_{Y_{\alpha }})\times _{(X, D_{X})} (Y_{\alpha ^{*}}, D_{Y_{\alpha ^{*}}})$
is equal to
![]() $dd^{*}(\ell \ell ^{*}(n_{X}-1)+1).$
We put
$dd^{*}(\ell \ell ^{*}(n_{X}-1)+1).$
We put
![]() $[\alpha ] \stackrel {\mathrm {def}}{=} \delta ([\alpha ^{*}])$
if
$[\alpha ] \stackrel {\mathrm {def}}{=} \delta ([\alpha ^{*}])$
if
![]() ${\vartheta }_{X}([\alpha ])={\vartheta }_{X}^{*}([\alpha ^{*}])$
. Moreover, by the construction above, we obtain that
${\vartheta }_{X}([\alpha ])={\vartheta }_{X}^{*}([\alpha ^{*}])$
. Moreover, by the construction above, we obtain that
![]() ${\vartheta }_{X}^{*}={\vartheta }_{X}\circ \delta $
. In a general case, we may choose an mp-triple
${\vartheta }_{X}^{*}={\vartheta }_{X}\circ \delta $
. In a general case, we may choose an mp-triple
associated to
![]() $(X, D_{X})$
, such that
$(X, D_{X})$
, such that
![]() $\ell ^{**} \neq \ell $
,
$\ell ^{**} \neq \ell $
,
![]() $\ell ^{**} \neq \ell ^{*}$
,
$\ell ^{**} \neq \ell ^{*}$
,
![]() $d^{**}\neq d$
, and
$d^{**}\neq d$
, and
![]() $d^{**} \neq d^{*}$
. Hence, we obtain a resulting set
$d^{**} \neq d^{*}$
. Hence, we obtain a resulting set
![]() $M_{Y^{**}}/\sim $
and a natural bijection,
$M_{Y^{**}}/\sim $
and a natural bijection,
![]() ${\vartheta }_{X}^{**}: M_{Y^{**}}/\sim \rightarrow D_{X}$
. Then the proof given above implies that there are natural bijections
${\vartheta }_{X}^{**}: M_{Y^{**}}/\sim \rightarrow D_{X}$
. Then the proof given above implies that there are natural bijections
![]() $\delta _{1}: M_{Y^{**}}/\sim \stackrel {\sim }{\rightarrow } M_{Y}/\sim $
and
$\delta _{1}: M_{Y^{**}}/\sim \stackrel {\sim }{\rightarrow } M_{Y}/\sim $
and
![]() $\delta _{2}: M_{Y^{**}}/\sim \stackrel {\sim }{\rightarrow } M_{Y^{*}}/\sim $
. Thus, we may put
$\delta _{2}: M_{Y^{**}}/\sim \stackrel {\sim }{\rightarrow } M_{Y^{*}}/\sim $
. Thus, we may put
Remark 3.3.2. Let
![]() $H \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X})$
be an arbitrary open normal subgroup and
$H \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X})$
be an arbitrary open normal subgroup and
![]() $f_{H}: (X_{H}, D_{X_{H}}) \rightarrow (X, D_{X})$
the Galois tame covering over k induced by the natural inclusion
$f_{H}: (X_{H}, D_{X_{H}}) \rightarrow (X, D_{X})$
the Galois tame covering over k induced by the natural inclusion
![]() $H \hookrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X})$
. Let
$H \hookrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X})$
. Let
be an mp-triple associated to
![]() $(X, D_{X})$
, such that
$(X, D_{X})$
, such that
![]() $(\#({\pi }_{1}^{\mathrm {t}}(U_{X})/H), \ell )=(\#({\pi }_{1}^{\mathrm {t}}(U_{X})/H), d)=1$
. Then we obtain an mp-triple
$(\#({\pi }_{1}^{\mathrm {t}}(U_{X})/H), \ell )=(\#({\pi }_{1}^{\mathrm {t}}(U_{X})/H), d)=1$
. Then we obtain an mp-triple
associated to
![]() $(X_{H}, D_{X_{H}})$
induced by
$(X_{H}, D_{X_{H}})$
induced by
![]() $(\ell , d, f: (Y, D_{Y}) \rightarrow (X, D_{X}))$
, where
$(\ell , d, f: (Y, D_{Y}) \rightarrow (X, D_{X}))$
, where
![]() $(Y, D_{Y}) \times _{(X, D_{X})} (X_{H}, D_{X_{H}})$
denotes the fiber product in the category of smooth pointed stable curves. The mp-triple associated to
$(Y, D_{Y}) \times _{(X, D_{X})} (X_{H}, D_{X_{H}})$
denotes the fiber product in the category of smooth pointed stable curves. The mp-triple associated to
![]() $(X_{H}, D_{X_{H}})$
induces a set
$(X_{H}, D_{X_{H}})$
induces a set
![]() $M_{Z}/\sim $
which can be identified with the set of marked points
$M_{Z}/\sim $
which can be identified with the set of marked points
![]() $D_{X_{H}}$
of
$D_{X_{H}}$
of
![]() $(X_{H}, D_{X_{H}})$
by applying Proposition 3.3. Moreover, for each
$(X_{H}, D_{X_{H}})$
by applying Proposition 3.3. Moreover, for each
![]() $e_{X} \in D_{X}$
and each
$e_{X} \in D_{X}$
and each
![]() $\alpha _{Y,e_{X}} \in M_{Y, e_{X}}$
,
$\alpha _{Y,e_{X}} \in M_{Y, e_{X}}$
,
![]() $\alpha _{Y, e_{X}}$
induces an element
$\alpha _{Y, e_{X}}$
induces an element
 $$ \begin{align*}\alpha_{Z}=\sum_{e_{X_{H}} \in f^{-1}_{H}(e_{X})} \alpha_{Z, e_{X_{H}}}\end{align*} $$
$$ \begin{align*}\alpha_{Z}=\sum_{e_{X_{H}} \in f^{-1}_{H}(e_{X})} \alpha_{Z, e_{X_{H}}}\end{align*} $$
over
![]() $(Z, D_{Z})$
via the natural morphism
$(Z, D_{Z})$
via the natural morphism
![]() $(Z, D_{Z}) \rightarrow (Y, D_{Y})$
, where
$(Z, D_{Z}) \rightarrow (Y, D_{Y})$
, where
![]() $\alpha _{Z, e_{X_{H}}} \in M_{Z, e_{X_{H}}}$
. On the other hand, for each
$\alpha _{Z, e_{X_{H}}} \in M_{Z, e_{X_{H}}}$
. On the other hand, for each
![]() $e^{\prime }_{X_{H}} \in D_{X_{H}}$
and each
$e^{\prime }_{X_{H}} \in D_{X_{H}}$
and each
![]() $e^{\prime }_{X} \in D_{X}$
, we have that
$e^{\prime }_{X} \in D_{X}$
, we have that
![]() $f_{H}(e^{\prime }_{X_{H}})=e^{\prime }_{X}$
if and only if there exists an element
$f_{H}(e^{\prime }_{X_{H}})=e^{\prime }_{X}$
if and only if there exists an element
![]() $\alpha _{Y, e^{\prime }_{X}} \in M_{Y, e^{\prime }_{X}}$
, such that the following conditions hold: (i) the element
$\alpha _{Y, e^{\prime }_{X}} \in M_{Y, e^{\prime }_{X}}$
, such that the following conditions hold: (i) the element
![]() $\alpha ^{\prime }_{Z}$
, induced by
$\alpha ^{\prime }_{Z}$
, induced by
![]() $\alpha _{Y, e^{\prime }_{X}}$
via the natural morphism
$\alpha _{Y, e^{\prime }_{X}}$
via the natural morphism
![]() $(Z, D_{Z}) \rightarrow (Y, D_{Y})$
, can be represented by a linear combination
$(Z, D_{Z}) \rightarrow (Y, D_{Y})$
, can be represented by a linear combination
 $$ \begin{align*}\alpha_{Z}'=\sum_{e_{X_{H}} \in S_{X_{H}}} \alpha^{\prime}_{Z, e_{X_{H}}},\end{align*} $$
$$ \begin{align*}\alpha_{Z}'=\sum_{e_{X_{H}} \in S_{X_{H}}} \alpha^{\prime}_{Z, e_{X_{H}}},\end{align*} $$
where
![]() $S_{X_{H}}$
is a subset of
$S_{X_{H}}$
is a subset of
![]() $D_{X_{H}}$
, and
$D_{X_{H}}$
, and
![]() $\alpha _{Z, e_{X_{H}}} \in M_{Z, e_{X_{H}}}$
; (ii)
$\alpha _{Z, e_{X_{H}}} \in M_{Z, e_{X_{H}}}$
; (ii)
![]() $e^{\prime }_{X_{H}} \in S_{X_{H}}$
.
$e^{\prime }_{X_{H}} \in S_{X_{H}}$
.
Lemma 3.4. Let
![]() $(\ell , d, f: (Y, D_{Y}) \rightarrow (X, D_{X}))$
be an mp-triple associated to
$(\ell , d, f: (Y, D_{Y}) \rightarrow (X, D_{X}))$
be an mp-triple associated to
![]() $(X, D_{X})$
and
$(X, D_{X})$
and
![]() $g_{Y}$
the genus of Y. Then we have
$g_{Y}$
the genus of Y. Then we have
![]() $\#(M_{Y, e})=\ell ^{2g_{Y}+1}-\ell ^{2g_{Y}}, \ e \in D_{X}.$
Moreover, we have
$\#(M_{Y, e})=\ell ^{2g_{Y}+1}-\ell ^{2g_{Y}}, \ e \in D_{X}.$
Moreover, we have
![]() $\#(M_{Y})=n_{X}(\ell ^{2g_{Y}+1}-\ell ^{2g_{Y}}).$
$\#(M_{Y})=n_{X}(\ell ^{2g_{Y}+1}-\ell ^{2g_{Y}}).$
Proof. Let
![]() $e \in D_{X}$
. Write
$e \in D_{X}$
. Write
![]() $D_{e} \subseteq D_{Y}$
for the set
$D_{e} \subseteq D_{Y}$
for the set
![]() $f^{-1}(e)$
. Then
$f^{-1}(e)$
. Then
![]() $M_{Y, e}$
can be naturally regarded as a subset of
$M_{Y, e}$
can be naturally regarded as a subset of
![]() $H^{1}_{\text {'et}}(Y \setminus D_{e}, \mathbb {F}_{\ell } )$
via the natural open immersion
$H^{1}_{\text {'et}}(Y \setminus D_{e}, \mathbb {F}_{\ell } )$
via the natural open immersion
![]() $Y\setminus D_{e} \hookrightarrow Y.$
Write
$Y\setminus D_{e} \hookrightarrow Y.$
Write
![]() $L_{e}$
for the
$L_{e}$
for the
![]() $\mathbb {F}_{\ell }$
-vector space generated by
$\mathbb {F}_{\ell }$
-vector space generated by
![]() $M_{Y, e}$
in
$M_{Y, e}$
in
![]() $H^{1}_{\text {'et}}(Y \setminus D_{e}, \mathbb {F}_{\ell })$
. Then we have
$H^{1}_{\text {'et}}(Y \setminus D_{e}, \mathbb {F}_{\ell })$
. Then we have
![]() $M_{Y, e}=\ L_{e}\setminus H^{1}_{\text {'et}}(Y, \mathbb {F}_{\ell }).$
Write
$M_{Y, e}=\ L_{e}\setminus H^{1}_{\text {'et}}(Y, \mathbb {F}_{\ell }).$
Write
![]() $H_{e}$
for the quotient
$H_{e}$
for the quotient
![]() $L_{e}/H^{1}_{\text {'et}}(Y, \mathbb {F}_{\ell })$
. We have an exact sequence as follows:
$L_{e}/H^{1}_{\text {'et}}(Y, \mathbb {F}_{\ell })$
. We have an exact sequence as follows:
Since the action of
![]() $\mu _{d}$
on
$\mu _{d}$
on
![]() $f^{-1}(e)$
is transitive, we obtain
$f^{-1}(e)$
is transitive, we obtain
![]() $\text {dim}_{\mathbb {F}_{\ell }}(H_{e})=1.$
On the other hand, since
$\text {dim}_{\mathbb {F}_{\ell }}(H_{e})=1.$
On the other hand, since
![]() $\text {dim}_{\mathbb {F}_{\ell }}(H^{1}_{\text {'et}}(Y, \mathbb {F}_{\ell }))=2g_{Y},$
we obtain
$\text {dim}_{\mathbb {F}_{\ell }}(H^{1}_{\text {'et}}(Y, \mathbb {F}_{\ell }))=2g_{Y},$
we obtain
![]() $\#(M_{Y, e})=\ell ^{2g_{Y}+1}-\ell ^{2g_{Y}}.$
Thus, we have
$\#(M_{Y, e})=\ell ^{2g_{Y}+1}-\ell ^{2g_{Y}}.$
Thus, we have
![]() $\#(M_{Y})=n_{X}(\ell ^{2g_{Y}+1}-\ell ^{2g_{Y}}).$
This completes the proof of the lemma.
$\#(M_{Y})=n_{X}(\ell ^{2g_{Y}+1}-\ell ^{2g_{Y}}).$
This completes the proof of the lemma.
3.3. Reconstructions of inertia subgroups
3.3.1. Settings
We maintain the notation introduced in Section 2.1.1.
3.3.2.
In this subsection, we will prove that the inertia subgroups of marked points can be mono-anabelian reconstructed from
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
(i.e., Proposition 3.7). The main idea is as follows: Let
${\pi }_{1}^{\mathrm {t}}(U_{X})$
(i.e., Proposition 3.7). The main idea is as follows: Let
![]() $H \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X})$
be an arbitrary normal open subgroup and
$H \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X})$
be an arbitrary normal open subgroup and
![]() $(X_{H}, D_{X_{H}}) \rightarrow (X, D_{X})$
the tame covering corresponding to H. Firstly, by using some numerical conditions induced by the Riemann-Hurwitz formula, the étale fundamental group
$(X_{H}, D_{X_{H}}) \rightarrow (X, D_{X})$
the tame covering corresponding to H. Firstly, by using some numerical conditions induced by the Riemann-Hurwitz formula, the étale fundamental group
![]() ${\pi }_{1}(X)$
can be mono-anabelian reconstructed from
${\pi }_{1}(X)$
can be mono-anabelian reconstructed from
![]() $\pi ^{\mathrm {t}}_{1}(U_{X})$
. Then the results obtained in Section 3.2 imply that
$\pi ^{\mathrm {t}}_{1}(U_{X})$
. Then the results obtained in Section 3.2 imply that
![]() $D_{X}$
can be mono-anabelian reconstructed from
$D_{X}$
can be mono-anabelian reconstructed from
![]() $\pi ^{\mathrm {t}}_{1}(U_{X})$
. Moreover,
$\pi ^{\mathrm {t}}_{1}(U_{X})$
. Moreover,
![]() $D_{X_{H}}$
can be also mono-anabelian reconstructed from H. Secondly, since the natural injection
$D_{X_{H}}$
can be also mono-anabelian reconstructed from H. Secondly, since the natural injection
![]() $H \hookrightarrow \pi ^{\mathrm {t}}_{1}(U_{X})$
induces a map of sets of cohomological classes obtained in Section 3.2, we obtain that the natural map
$H \hookrightarrow \pi ^{\mathrm {t}}_{1}(U_{X})$
induces a map of sets of cohomological classes obtained in Section 3.2, we obtain that the natural map
![]() $D_{X_{H}} \rightarrow D_{X}$
can be mono-anabelian reconstructed from
$D_{X_{H}} \rightarrow D_{X}$
can be mono-anabelian reconstructed from
![]() $H \hookrightarrow \pi ^{\mathrm { t}}_{1}(U_{X})$
. Thus, by taking a cofinal system of open normal subgroups of
$H \hookrightarrow \pi ^{\mathrm { t}}_{1}(U_{X})$
. Thus, by taking a cofinal system of open normal subgroups of
![]() $\pi ^{\mathrm {t}}_{1}(U_{X})$
, we obtain a new mono-anabelian reconstruction of
$\pi ^{\mathrm {t}}_{1}(U_{X})$
, we obtain a new mono-anabelian reconstruction of
![]() $\text {Ine}({\pi }_{1}^{\mathrm {t}}(U_{X}))$
.
$\text {Ine}({\pi }_{1}^{\mathrm {t}}(U_{X}))$
.
3.3.3.
First, we have the following lemma.
Lemma 3.5.
(i) The prime number p (i.e., the characteristic of k) can be mono-anabelian reconstructed from
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
.
${\pi }_{1}^{\mathrm {t}}(U_{X})$
.
(ii) The étale fundamental group
![]() ${\pi }_{1}(X)$
can be mono-anabelian reconstructed from
${\pi }_{1}(X)$
can be mono-anabelian reconstructed from
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
.
${\pi }_{1}^{\mathrm {t}}(U_{X})$
.
Proof. (i) Let
![]() $\mathfrak {P}$
be the set of prime numbers, and let Q be an arbitrary open subgroup of
$\mathfrak {P}$
be the set of prime numbers, and let Q be an arbitrary open subgroup of
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
and
${\pi }_{1}^{\mathrm {t}}(U_{X})$
and
![]() $r_{Q}$
an integer, such that
$r_{Q}$
an integer, such that
Then we see immediately that the characteristic of k is the unique prime number p, such that there exists an open subgroup
![]() $T \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X})$
and
$T \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X})$
and
![]() $r_{T}\neq \text {dim}_{\mathbb {F}_{p}}(T^{\mathrm {ab}}\otimes \mathbb {F}_{p}).$
$r_{T}\neq \text {dim}_{\mathbb {F}_{p}}(T^{\mathrm {ab}}\otimes \mathbb {F}_{p}).$
(ii) Let H be an arbitrary open normal subgroup of
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
. We denote by
${\pi }_{1}^{\mathrm {t}}(U_{X})$
. We denote by
![]() $(X_{H}, D_{X_{H}})$
the smooth pointed stable curve of type
$(X_{H}, D_{X_{H}})$
the smooth pointed stable curve of type
![]() $(g_{X_{H}}, n_{X_{H}})$
over k induced by H, and denote by
$(g_{X_{H}}, n_{X_{H}})$
over k induced by H, and denote by
![]() $f_{H}: (X_{H}, D_{X_{H}}) \rightarrow (X, D_{X})$
the morphism of smooth pointed stable curves over k induced by the natural inclusion
$f_{H}: (X_{H}, D_{X_{H}}) \rightarrow (X, D_{X})$
the morphism of smooth pointed stable curves over k induced by the natural inclusion
![]() $H \hookrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X})$
. We note that
$H \hookrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X})$
. We note that
![]() $f_{H}$
is étale if and only if
$f_{H}$
is étale if and only if
![]() $g_{X_{H}}-1=\#({\pi }_{1}^{\mathrm {t}}(U_X)/H)(g_{X}-1).$
We put
$g_{X_{H}}-1=\#({\pi }_{1}^{\mathrm {t}}(U_X)/H)(g_{X}-1).$
We put
Moreover, Proposition 3.2 (i) implies that
![]() $g_{X_{H}}$
and
$g_{X_{H}}$
and
![]() $g_{X}$
can be mono-anabelian reconstructed from H and
$g_{X}$
can be mono-anabelian reconstructed from H and
![]() ${\pi }_{1}^{\mathrm {t}}(U_X)$
, respectively. Then the set
${\pi }_{1}^{\mathrm {t}}(U_X)$
, respectively. Then the set
![]() $\text {Et}({\pi }_{1}^{\mathrm {t}}(U_X))$
can be mono-anabelian reconstructed from
$\text {Et}({\pi }_{1}^{\mathrm {t}}(U_X))$
can be mono-anabelian reconstructed from
![]() ${\pi }_{1}^{\mathrm {t}}(U_X)$
. We obtain that
${\pi }_{1}^{\mathrm {t}}(U_X)$
. We obtain that
 $$ \begin{align*}{\pi}_{1}(X)= {\pi}_{1}^{\mathrm{t}}(U_{X})/\bigcap_{H \in \text{Et}({\pi}_{1}^{\mathrm{t}}(U_{X}))}H .\end{align*} $$
$$ \begin{align*}{\pi}_{1}(X)= {\pi}_{1}^{\mathrm{t}}(U_{X})/\bigcap_{H \in \text{Et}({\pi}_{1}^{\mathrm{t}}(U_{X}))}H .\end{align*} $$
This completes the proof of the lemma.
3.3.4.
Suppose
![]() $g_{X} \geq 2$
. Let us define a group-theoretical object corresponding to an mp-triple, which was introduced in Section 3.2.3. We shall say that
$g_{X} \geq 2$
. Let us define a group-theoretical object corresponding to an mp-triple, which was introduced in Section 3.2.3. We shall say that
is an mp-triple associated to
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
if the following conditions hold: (i)
${\pi }_{1}^{\mathrm {t}}(U_{X})$
if the following conditions hold: (i)
![]() $\ell $
and d are prime numbers distinct from each other, such that
$\ell $
and d are prime numbers distinct from each other, such that
![]() $(\ell , p)=(d, p)=1$
and
$(\ell , p)=(d, p)=1$
and
![]() $\ell \equiv 1 \ (\text {mod}\ d)$
; then all dth roots of unity are contained in
$\ell \equiv 1 \ (\text {mod}\ d)$
; then all dth roots of unity are contained in
![]() $\mathbb {F}_{\ell }$
; (ii)
$\mathbb {F}_{\ell }$
; (ii)
![]() $y \in \text {Hom}({\pi }_{1}(X), \mu _{d})$
, such that
$y \in \text {Hom}({\pi }_{1}(X), \mu _{d})$
, such that
![]() $y\neq 0$
, where
$y\neq 0$
, where
![]() $\mu _{d} \subseteq \mathbb {F}_{\ell }^{\times }$
denotes the subgroup of dth roots of unity.
$\mu _{d} \subseteq \mathbb {F}_{\ell }^{\times }$
denotes the subgroup of dth roots of unity.
3.3.5.
Moreover, by applying Lemma 3.5, there is a triple
![]() $(\ell , d, y)$
associated to
$(\ell , d, y)$
associated to
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
which can be mono-anabelian reconstructed from
${\pi }_{1}^{\mathrm {t}}(U_{X})$
which can be mono-anabelian reconstructed from
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
. Let
${\pi }_{1}^{\mathrm {t}}(U_{X})$
. Let
![]() $f: (Y, D_{Y}) \rightarrow (X, D_{X})$
be a Galois étale covering induced by y. Then we see immediately that
$f: (Y, D_{Y}) \rightarrow (X, D_{X})$
be a Galois étale covering induced by y. Then we see immediately that
![]() $(\ell , d, f: (Y, D_{Y}) \rightarrow (X, D_{X}))$
is an mp-triple associated to
$(\ell , d, f: (Y, D_{Y}) \rightarrow (X, D_{X}))$
is an mp-triple associated to
![]() $(X, D_{X})$
defined in Section 3.2.3. We denote by
$(X, D_{X})$
defined in Section 3.2.3. We denote by
![]() ${\pi }_{1}^{\mathrm {t}}(U_{Y})$
the kernel of the composition of the surjections
${\pi }_{1}^{\mathrm {t}}(U_{Y})$
the kernel of the composition of the surjections
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X}) \twoheadrightarrow {\pi }_{1}(X) \overset {y}{\twoheadrightarrow } \mu _{d}.$
Since
${\pi }_{1}^{\mathrm {t}}(U_{X}) \twoheadrightarrow {\pi }_{1}(X) \overset {y}{\twoheadrightarrow } \mu _{d}.$
Since
![]() $H^{1}_{\text {'et}}(Y, \mathbb {F}_{\ell }) \cong \text {Hom}({\pi }_{1}(Y), \mathbb {F}_{\ell })$
and
$H^{1}_{\text {'et}}(Y, \mathbb {F}_{\ell }) \cong \text {Hom}({\pi }_{1}(Y), \mathbb {F}_{\ell })$
and
![]() $H^{1}_{\text {'et}}(U_Y, \mathbb {F}_{\ell }) \cong \text {Hom}(\pi ^{\mathrm {t}}_{1}(U_{Y}), \mathbb {F}_{\ell })$
, Lemma 3.5 implies immediately that the following exact sequence
$H^{1}_{\text {'et}}(U_Y, \mathbb {F}_{\ell }) \cong \text {Hom}(\pi ^{\mathrm {t}}_{1}(U_{Y}), \mathbb {F}_{\ell })$
, Lemma 3.5 implies immediately that the following exact sequence
can be mono-anabelian reconstructed from
![]() ${\pi }_{1}^{\mathrm {t}}(U_{Y})$
. Thus, Proposition 3.2 (i) implies that the set
${\pi }_{1}^{\mathrm {t}}(U_{Y})$
. Thus, Proposition 3.2 (i) implies that the set
![]() $M_{Y}/\sim $
defined in Section 3.2.5 can be mono-anabelian reconstructed from
$M_{Y}/\sim $
defined in Section 3.2.5 can be mono-anabelian reconstructed from
![]() ${\pi }_{1}^{\mathrm {t}}(U_{Y})$
. Note that, by Remark 3.3.1, the set
${\pi }_{1}^{\mathrm {t}}(U_{Y})$
. Note that, by Remark 3.3.1, the set
![]() $M_{Y}/\sim $
does not depend on the choices of mp-triples. Then we put
$M_{Y}/\sim $
does not depend on the choices of mp-triples. Then we put
where
![]() $(-)^{\mathrm {gp}}$
means “group-theoretical.” By Proposition 3.3, we may identify
$(-)^{\mathrm {gp}}$
means “group-theoretical.” By Proposition 3.3, we may identify
![]() $D^{\mathrm {gp}}_{X}$
with the set of marked points
$D^{\mathrm {gp}}_{X}$
with the set of marked points
![]() $D_{X}$
of
$D_{X}$
of
![]() $(X, D_{X})$
via the bijection
$(X, D_{X})$
via the bijection
![]() ${\vartheta }_{X}: D^{\mathrm {gp}}_{X} \stackrel {\sim }{\rightarrow } D_{X}$
defined in Proposition 3.3.
${\vartheta }_{X}: D^{\mathrm {gp}}_{X} \stackrel {\sim }{\rightarrow } D_{X}$
defined in Proposition 3.3.
Proposition 3.6. Let
![]() $H \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X})$
be an arbitrary open normal subgroup and
$H \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X})$
be an arbitrary open normal subgroup and
the morphism of smooth pointed stable curves over k induced by the natural inclusion
![]() $H \hookrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X})$
. Suppose
$H \hookrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X})$
. Suppose
![]() $g_{X} \geq 2$
. Then the sets
$g_{X} \geq 2$
. Then the sets
![]() $D_{X}^{\mathrm {gp}}$
and
$D_{X}^{\mathrm {gp}}$
and
![]() $D_{X_{H}}^{\mathrm {gp}}$
can be mono-anabelian reconstructed from
$D_{X_{H}}^{\mathrm {gp}}$
can be mono-anabelian reconstructed from
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
and H, respectively. Moreover, the inclusion
${\pi }_{1}^{\mathrm {t}}(U_{X})$
and H, respectively. Moreover, the inclusion
![]() $H \hookrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X})$
induces a map
$H \hookrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X})$
induces a map
![]() $\gamma _{H, {\pi }_{1}^{\mathrm {t}}(U_{X})}: D_{X_{H}}^{\mathrm {gp}} \rightarrow D_{X}^{\mathrm {gp}}$
, such that the following commutative diagram holds:
$\gamma _{H, {\pi }_{1}^{\mathrm {t}}(U_{X})}: D_{X_{H}}^{\mathrm {gp}} \rightarrow D_{X}^{\mathrm {gp}}$
, such that the following commutative diagram holds:

where
![]() $\gamma _{f_{H}}$
denotes the map of the sets of marked points induced by
$\gamma _{f_{H}}$
denotes the map of the sets of marked points induced by
![]() $f_{H}$
.
$f_{H}$
.
Proof. We only need to prove the “moreover” part of Proposition 3.6. We maintain the notation introduced in Remark 3.3.2. Note that, for each
![]() $e_{X} \in D_{X}$
and each
$e_{X} \in D_{X}$
and each
![]() $e_{X_{H}} \in D_{X_{H}}$
, the sets
$e_{X_{H}} \in D_{X_{H}}$
, the sets
![]() $M_{Y, e_{X}}$
and
$M_{Y, e_{X}}$
and
![]() $M_{Z, e_{X_{H}}}$
can be mono-anabelian reconstructed from
$M_{Z, e_{X_{H}}}$
can be mono-anabelian reconstructed from
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
and H, respectively. Then the “moreover” part follows from Remark 3.3.2.
${\pi }_{1}^{\mathrm {t}}(U_{X})$
and H, respectively. Then the “moreover” part follows from Remark 3.3.2.
Remark 3.6.1. We maintain the notation introduced in Proposition 3.6. Let
![]() ${\pi }_{1}(X_{H})$
be the étale fundamental group of
${\pi }_{1}(X_{H})$
be the étale fundamental group of
![]() $X_{H}$
. Then we have a natural surjection
$X_{H}$
. Then we have a natural surjection
![]() $H \twoheadrightarrow {\pi }_{1}(X_{H})$
. Note that
$H \twoheadrightarrow {\pi }_{1}(X_{H})$
. Note that
![]() ${\pi }_{1}(X_{H})$
admits an action of
${\pi }_{1}(X_{H})$
admits an action of
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})/H$
induced by the outer action of
${\pi }_{1}^{\mathrm {t}}(U_{X})/H$
induced by the outer action of
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})/H$
on H induced by the exact sequence
${\pi }_{1}^{\mathrm {t}}(U_{X})/H$
on H induced by the exact sequence
Moreover, the action of
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})/H$
on
${\pi }_{1}^{\mathrm {t}}(U_{X})/H$
on
![]() ${\pi }_{1}(X_{H})$
induces an action of
${\pi }_{1}(X_{H})$
induces an action of
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})/H$
on
${\pi }_{1}^{\mathrm {t}}(U_{X})/H$
on
![]() $D^{\mathrm { gp}}_{X_{H}}$
. On the other hand, it is easy to check that the action of
$D^{\mathrm { gp}}_{X_{H}}$
. On the other hand, it is easy to check that the action of
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})/H$
on
${\pi }_{1}^{\mathrm {t}}(U_{X})/H$
on
![]() $D^{\mathrm {gp}}_{X_{H}}$
coincides with the natural action of
$D^{\mathrm {gp}}_{X_{H}}$
coincides with the natural action of
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})/H$
on
${\pi }_{1}^{\mathrm {t}}(U_{X})/H$
on
![]() $D_{X_{H}}$
when we identify
$D_{X_{H}}$
when we identify
![]() $D_{X}^{\mathrm {gp}}$
with
$D_{X}^{\mathrm {gp}}$
with
![]() $D_{X}$
.
$D_{X}$
.
3.3.6.
We have the following result.
Proposition 3.7. Write
![]() $\mathrm {Ine}({\pi }_{1}^{\mathrm {t}}(U_{X}))$
for the set of inertia subgroups in
$\mathrm {Ine}({\pi }_{1}^{\mathrm {t}}(U_{X}))$
for the set of inertia subgroups in
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
. Then
${\pi }_{1}^{\mathrm {t}}(U_{X})$
. Then
![]() $\mathrm {Ine}({\pi }_{1}^{\mathrm {t}}(U_{X}))$
can be mono-anabelian reconstructed from
$\mathrm {Ine}({\pi }_{1}^{\mathrm {t}}(U_{X}))$
can be mono-anabelian reconstructed from
![]() ${\pi }_{1}^{\mathrm { t}}(U_{X})$
.
${\pi }_{1}^{\mathrm { t}}(U_{X})$
.
Proof. Let
![]() $C_{X}\stackrel {\mathrm {def}}{=} \{H_{i}\}_{i \in \mathbb {Z}_{> 0}}$
be a set of open normal subgroups of
$C_{X}\stackrel {\mathrm {def}}{=} \{H_{i}\}_{i \in \mathbb {Z}_{> 0}}$
be a set of open normal subgroups of
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
, such that
${\pi }_{1}^{\mathrm {t}}(U_{X})$
, such that
![]() $\varprojlim _{i}{\pi }_{1}^{\mathrm {t}}(U_{X})/H_{i} \cong {\pi }_{1}^{\mathrm { t}}(U_{X})$
(i.e., a cofinal system of open normal subgroups).
$\varprojlim _{i}{\pi }_{1}^{\mathrm {t}}(U_{X})/H_{i} \cong {\pi }_{1}^{\mathrm { t}}(U_{X})$
(i.e., a cofinal system of open normal subgroups).
Let
![]() $\widetilde e \in D_{\widetilde X}$
. For each
$\widetilde e \in D_{\widetilde X}$
. For each
![]() $i \in \mathbb {Z}_{> 0}$
, we write
$i \in \mathbb {Z}_{> 0}$
, we write
![]() $(X_{H_{i}}, D_{X_{H_{i}}})$
for the smooth pointed stable curve of type
$(X_{H_{i}}, D_{X_{H_{i}}})$
for the smooth pointed stable curve of type
![]() $(g_{X_{H_{i}}}, n_{X_{H_{i}}})$
induced by
$(g_{X_{H_{i}}}, n_{X_{H_{i}}})$
induced by
![]() $H_{i}$
and
$H_{i}$
and
![]() $e_{X_{H_{i}}} \in D_{X_{H_{i}}}$
for the image of
$e_{X_{H_{i}}} \in D_{X_{H_{i}}}$
for the image of
![]() $\widetilde e$
. Then we obtain a sequence of marked points
$\widetilde e$
. Then we obtain a sequence of marked points
induced by
![]() $C_{X}$
. Note that the sequence
$C_{X}$
. Note that the sequence
![]() $\mathcal {I}^{C_{X}}_{\widetilde e}$
admits a natural action of
$\mathcal {I}^{C_{X}}_{\widetilde e}$
admits a natural action of
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
. We may identify the inertia subgroup
${\pi }_{1}^{\mathrm {t}}(U_{X})$
. We may identify the inertia subgroup
![]() $I_{\widetilde e}$
associated to
$I_{\widetilde e}$
associated to
![]() $\widetilde e$
with the stabilizer of
$\widetilde e$
with the stabilizer of
![]() $\mathcal {I}^{C_{X}}_{\widetilde e}$
.
$\mathcal {I}^{C_{X}}_{\widetilde e}$
.
Moreover, since Proposition 3.2 (i) implies that
![]() $(g_{X_{H_{i}}}, n_{X_{H_{i}}})$
can be mono-anabelian reconstructed from
$(g_{X_{H_{i}}}, n_{X_{H_{i}}})$
can be mono-anabelian reconstructed from
![]() $H_{i}$
, by choosing a suitable set of open normal subgroups
$H_{i}$
, by choosing a suitable set of open normal subgroups
![]() $C_{X}$
, we may assume that
$C_{X}$
, we may assume that
![]() $g_{X_{H_{1}}}\geq 2$
. If
$g_{X_{H_{1}}}\geq 2$
. If
![]() $n_{X_{H_{1}}}=0$
, Proposition 3.7 is trivial. Then we may assume that
$n_{X_{H_{1}}}=0$
, Proposition 3.7 is trivial. Then we may assume that
![]() $n_{X_{H_{1}}}> 0$
.
$n_{X_{H_{1}}}> 0$
.
On the other hand, Proposition 3.6 implies that, for each
![]() $H_{i}$
,
$H_{i}$
,
![]() $i\in \mathbb {Z}_{> 0}$
, the set
$i\in \mathbb {Z}_{> 0}$
, the set
![]() $D^{\mathrm {gp}}_{X_{H_{i}}}$
can be mono-anabelian reconstructed from
$D^{\mathrm {gp}}_{X_{H_{i}}}$
can be mono-anabelian reconstructed from
![]() $H_{i}$
. For each
$H_{i}$
. For each
![]() $e_{X_{H_{i}}} \in D_{X_{H_{i}}}$
, we denote by
$e_{X_{H_{i}}} \in D_{X_{H_{i}}}$
, we denote by
Then the sequence of marked points
![]() $\mathcal {I}^{C_{X}}_{\widetilde e}$
induces a sequence
$\mathcal {I}^{C_{X}}_{\widetilde e}$
induces a sequence
By applying the “moreover” part of Proposition 3.6, we see that
![]() $\mathcal {I}^{C_{X}}_{\widetilde e^{\mathrm {gp}}}$
can be mono-anabelian reconstructed from
$\mathcal {I}^{C_{X}}_{\widetilde e^{\mathrm {gp}}}$
can be mono-anabelian reconstructed from
![]() $C_{X}$
. Then Remark 3.6.1 implies that the stabilizer of
$C_{X}$
. Then Remark 3.6.1 implies that the stabilizer of
![]() $\mathcal {I}^{C_{X}}_{\widetilde e^{\mathrm {gp}}}$
is equal to the stabilizer of
$\mathcal {I}^{C_{X}}_{\widetilde e^{\mathrm {gp}}}$
is equal to the stabilizer of
![]() $\mathcal {I}^{C_{X}}_{\widetilde e}$
. This completes the proof of the proposition.
$\mathcal {I}^{C_{X}}_{\widetilde e}$
. This completes the proof of the proposition.
3.4. Reconstructions of inertia subgroups via surjections
3.4.1. Settings
Let
![]() $(X_{i}, D_{X_{i}})$
,
$(X_{i}, D_{X_{i}})$
,
![]() $i \in \{1, 2\}$
, be a smooth pointed stable curve of type
$i \in \{1, 2\}$
, be a smooth pointed stable curve of type
![]() $(g_{X}, n_{X})$
over an algebraically closed field
$(g_{X}, n_{X})$
over an algebraically closed field
![]() $k_{i}$
of characteristic
$k_{i}$
of characteristic
![]() $p>0$
,
$p>0$
,
![]() $U_{X_i}\stackrel {\mathrm {def}}{=} X_{i} \setminus D_{X_{i}}$
,
$U_{X_i}\stackrel {\mathrm {def}}{=} X_{i} \setminus D_{X_{i}}$
,
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
the tame fundamental group of
${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
the tame fundamental group of
![]() $U_{X_{i}}$
, and
$U_{X_{i}}$
, and
![]() ${\pi }_{1}(X_{i})$
the étale fundamental group of
${\pi }_{1}(X_{i})$
the étale fundamental group of
![]() $X_{i}$
. Then Lemma 3.5 implies that
$X_{i}$
. Then Lemma 3.5 implies that
![]() ${\pi }_{1}(X_{i})$
can be mono-anabelian reconstructed from
${\pi }_{1}(X_{i})$
can be mono-anabelian reconstructed from
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
. Moreover, in this subsection, we suppose that
${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
. Moreover, in this subsection, we suppose that
![]() $n_{X}>0$
, and that
$n_{X}>0$
, and that
![]() $\phi : {\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
is an arbitrary open continuous surjective homomorphism of profinite groups.
$\phi : {\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
is an arbitrary open continuous surjective homomorphism of profinite groups.
Note that, since
![]() $(X_{i}, D_{X_{i}})$
,
$(X_{i}, D_{X_{i}})$
,
![]() $i\in \{1, 2\}$
, is a smooth pointed stable curve of type
$i\in \{1, 2\}$
, is a smooth pointed stable curve of type
![]() $(g_{X}, n_{X})$
,
$(g_{X}, n_{X})$
,
![]() $\phi $
induces a natural surjection
$\phi $
induces a natural surjection
![]() $\phi ^{p'}: {\pi }_{1}^{\mathrm {t}}(U_{X_{1}})^{p'} \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})^{p'}$
, where
$\phi ^{p'}: {\pi }_{1}^{\mathrm {t}}(U_{X_{1}})^{p'} \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})^{p'}$
, where
![]() $(-)^{p'}$
denotes the maximal prime-to-p quotient of
$(-)^{p'}$
denotes the maximal prime-to-p quotient of
![]() $(-)$
. Since
$(-)$
. Since
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})^{p'}$
,
${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})^{p'}$
,
![]() $i \in \{1, 2\}$
, is topologically finitely generated, and
$i \in \{1, 2\}$
, is topologically finitely generated, and
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})^{p'}$
is isomorphic to
${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})^{p'}$
is isomorphic to
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{2}})^{p'}$
as abstract profinite groups, we obtain that
${\pi }_{1}^{\mathrm {t}}(U_{X_{2}})^{p'}$
as abstract profinite groups, we obtain that
![]() $\phi ^{p'}: {\pi }_{1}^{\mathrm {t}}(U_{X_{1}})^{p'} \stackrel {\sim }{\rightarrow } {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})^{p'}$
is an isomorphism ([Reference Fried and JardenFJ, Proposition 16.10.6]).
$\phi ^{p'}: {\pi }_{1}^{\mathrm {t}}(U_{X_{1}})^{p'} \stackrel {\sim }{\rightarrow } {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})^{p'}$
is an isomorphism ([Reference Fried and JardenFJ, Proposition 16.10.6]).
3.4.2.
In this subsection, we will prove that the mono-anabelian reconstructions obtained in Proposition 3.7 are compatible with any open continuous homomorphisms (i.e., Theorem 3.14). We explain the main idea. Let
![]() $H_{2} \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
be an arbitrary open normal subgroup and
$H_{2} \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
be an arbitrary open normal subgroup and
![]() $H_{1}\stackrel {\mathrm {def}}{=} \phi ^{-1}(H_{2}) \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{1}})$
. We write
$H_{1}\stackrel {\mathrm {def}}{=} \phi ^{-1}(H_{2}) \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{1}})$
. We write
![]() $(X_{H_i}, D_{X_{H_i}})$
,
$(X_{H_i}, D_{X_{H_i}})$
,
![]() $i\in \{1, 2\}$
, for the smooth pointed smooth curve of type
$i\in \{1, 2\}$
, for the smooth pointed smooth curve of type
![]() $(g_{X_{H_{i}}}, n_{X_{H_i}})$
over
$(g_{X_{H_{i}}}, n_{X_{H_i}})$
over
![]() $k_{i}$
induced by
$k_{i}$
induced by
![]() $H_{i}$
. To prove the compatibility, we need to prove that, for any prime number
$H_{i}$
. To prove the compatibility, we need to prove that, for any prime number
![]() $\ell \neq p$
, the weight-monodromy filtration of
$\ell \neq p$
, the weight-monodromy filtration of
![]() $H_{2}^{\mathrm {ab}}\otimes \mathbb {F}_{\ell }$
induces the weight-monodromy filtration of
$H_{2}^{\mathrm {ab}}\otimes \mathbb {F}_{\ell }$
induces the weight-monodromy filtration of
![]() $H_{1}^{\mathrm {ab}}\otimes \mathbb {F}_{\ell }$
via the natural surjection
$H_{1}^{\mathrm {ab}}\otimes \mathbb {F}_{\ell }$
via the natural surjection
![]() $\phi |_{H_{1}}: H_{1} \twoheadrightarrow H_{2}$
. Note that the weight
$\phi |_{H_{1}}: H_{1} \twoheadrightarrow H_{2}$
. Note that the weight
![]() $1$
part of
$1$
part of
![]() $H_{i}^{\mathrm {ab}}\otimes \mathbb {F}_{\ell }$
corresponds to
$H_{i}^{\mathrm {ab}}\otimes \mathbb {F}_{\ell }$
corresponds to
![]() ${\pi }_{1}(X_{H_{i}})^{\mathrm {ab}}\otimes \mathbb {F}_{\ell }$
, and the weight
${\pi }_{1}(X_{H_{i}})^{\mathrm {ab}}\otimes \mathbb {F}_{\ell }$
, and the weight
![]() $2$
part of
$2$
part of
![]() $H_{i}^{\mathrm { ab}}\otimes \mathbb {F}_{\ell }$
corresponds to the image of the subgroup of
$H_{i}^{\mathrm { ab}}\otimes \mathbb {F}_{\ell }$
corresponds to the image of the subgroup of
![]() $H_{i}$
generated by the inertia subgroups of the marked points of
$H_{i}$
generated by the inertia subgroups of the marked points of
![]() $D_{X_{H_{i}}}$
. The key observation is as follows:
$D_{X_{H_{i}}}$
. The key observation is as follows:
The inequality of the limit of p-averages (see Proposition 3.8 (i) below)
of
![]() $H_1$
and
$H_1$
and
![]() $H_2$
induced by the surjection
$H_2$
induced by the surjection
![]() $\phi |_{H_{1}}: H_{1} \twoheadrightarrow H_{2}$
plays a role of the comparability of “Galois actions” in the theory of the anabelian geometry of curves over algebraically closed fields of characteristic
$\phi |_{H_{1}}: H_{1} \twoheadrightarrow H_{2}$
plays a role of the comparability of “Galois actions” in the theory of the anabelian geometry of curves over algebraically closed fields of characteristic
![]() $p>0$
.
$p>0$
.
3.4.3.
Firstly, we have the following proposition.
Proposition 3.8.
(i) Let
![]() $(X, D_{X})$
be a pointed stable curve of type
$(X, D_{X})$
be a pointed stable curve of type
![]() $(g_{X}, n_{X})$
over an algebraically closed field k of characteristic
$(g_{X}, n_{X})$
over an algebraically closed field k of characteristic
![]() $p>0$
,
$p>0$
,
![]() $U_{X} \stackrel {\mathrm {def}}{=} X \setminus D_{X}$
, and
$U_{X} \stackrel {\mathrm {def}}{=} X \setminus D_{X}$
, and
![]() $\pi ^{\mathrm {t}}_{1}(U_{X})$
the tame fundamental group of
$\pi ^{\mathrm {t}}_{1}(U_{X})$
the tame fundamental group of
![]() $U_{X}$
. Let
$U_{X}$
. Let
![]() $r \in \mathbb {N}$
be a natural number, and let
$r \in \mathbb {N}$
be a natural number, and let
![]() $K_{p^{r}-1}$
be the kernel of the natural surjection
$K_{p^{r}-1}$
be the kernel of the natural surjection
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X})^{\mathrm {ab}} \otimes \mathbb {Z}/(p^{r}-1)\mathbb {Z}$
, where
${\pi }_{1}^{\mathrm {t}}(U_{X}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X})^{\mathrm {ab}} \otimes \mathbb {Z}/(p^{r}-1)\mathbb {Z}$
, where
![]() $(-)^{\mathrm {ab}}$
denotes the abelianization of
$(-)^{\mathrm {ab}}$
denotes the abelianization of
![]() $(-)$
. Then we have
$(-)$
. Then we have
 $$ \begin{align*} \mathrm{Avr}_{p}({\pi}_{1}^{\mathrm{t}}(U_{X})) \stackrel{\mathrm{def}}{=} \lim_{r\rightarrow\infty}\frac{\mathrm{dim}_{\mathbb{F}_{p}}(K^{\mathrm{ab}}_{p^{r}-1} \otimes \mathbb{F}_{p})}{\#( {\pi}_{1}^{\mathrm{t}}(U_{X})^{\mathrm{ab}} \otimes \mathbb{Z}/(p^{r}-1)\mathbb{Z})}= \left\{ \begin{array}{ll} g_{X}-1, & \text{if} \ n_{X}\leq 1, \\ g_{X}, & \text{if} \ n_{X}> 1. \end{array} \right. \end{align*} $$
$$ \begin{align*} \mathrm{Avr}_{p}({\pi}_{1}^{\mathrm{t}}(U_{X})) \stackrel{\mathrm{def}}{=} \lim_{r\rightarrow\infty}\frac{\mathrm{dim}_{\mathbb{F}_{p}}(K^{\mathrm{ab}}_{p^{r}-1} \otimes \mathbb{F}_{p})}{\#( {\pi}_{1}^{\mathrm{t}}(U_{X})^{\mathrm{ab}} \otimes \mathbb{Z}/(p^{r}-1)\mathbb{Z})}= \left\{ \begin{array}{ll} g_{X}-1, & \text{if} \ n_{X}\leq 1, \\ g_{X}, & \text{if} \ n_{X}> 1. \end{array} \right. \end{align*} $$
(ii) We maintain the setting introduced in Section 3.4.1. Let
![]() $H_{2} \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
be an open normal subgroup, such that
$H_{2} \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
be an open normal subgroup, such that
![]() $([{\pi }_{1}^{\mathrm {t}}(U_{X_{2}}): H_{2}], p)=1$
and
$([{\pi }_{1}^{\mathrm {t}}(U_{X_{2}}): H_{2}], p)=1$
and
![]() $H_{1} \stackrel {\mathrm {def}}{=} \phi ^{-1}(H_{2})$
. Write
$H_{1} \stackrel {\mathrm {def}}{=} \phi ^{-1}(H_{2})$
. Write
![]() $g_{H_{i}}$
,
$g_{H_{i}}$
,
![]() $i\in \{1, 2\}$
, for the genus of the smooth pointed stable curve over
$i\in \{1, 2\}$
, for the genus of the smooth pointed stable curve over
![]() $k_{i}$
corresponding to
$k_{i}$
corresponding to
![]() $H_{i} \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
. Then we have
$H_{i} \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
. Then we have
![]() $g_{H_{1}} \geq g_{H_{2}}.$
$g_{H_{1}} \geq g_{H_{2}}.$
Proof. (i) is the Tamagawa’s result concerning the limit of p-averages of
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
([Reference TamagawaT4, Theorem 0.5]). Let us prove (ii). The surjection
${\pi }_{1}^{\mathrm {t}}(U_{X})$
([Reference TamagawaT4, Theorem 0.5]). Let us prove (ii). The surjection
![]() $\phi $
induces a surjection
$\phi $
induces a surjection
![]() $\phi ^{p'}: \pi ^{\mathrm {t}}_{1}(U_{X_{1}})^{p'} \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})^{p'},$
where
$\phi ^{p'}: \pi ^{\mathrm {t}}_{1}(U_{X_{1}})^{p'} \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})^{p'},$
where
![]() $(-)^{p'}$
denotes the maximal prime-to-p quotient of
$(-)^{p'}$
denotes the maximal prime-to-p quotient of
![]() $(-)$
. Moreover, since
$(-)$
. Moreover, since
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})^{p'}$
,
${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})^{p'}$
,
![]() $i \in \{1, 2\}$
, is topologically finitely generated, and
$i \in \{1, 2\}$
, is topologically finitely generated, and
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})^{p'}$
is isomorphic to
${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})^{p'}$
is isomorphic to
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{2}})^{p'}$
as abstract profinite groups (since the types of
${\pi }_{1}^{\mathrm {t}}(U_{X_{2}})^{p'}$
as abstract profinite groups (since the types of
![]() $(X_{1}, D_{X_{1}})$
and
$(X_{1}, D_{X_{1}})$
and
![]() $(X_{2}, D_{X_{2}})$
are equal to
$(X_{2}, D_{X_{2}})$
are equal to
![]() $(g_{X}, n_{X})$
), we obtain that
$(g_{X}, n_{X})$
), we obtain that
![]() $\phi ^{p'}$
is an isomorphism (cf. [Reference Fried and JardenFJ, Proposition 16.10.6]).
$\phi ^{p'}$
is an isomorphism (cf. [Reference Fried and JardenFJ, Proposition 16.10.6]).
On the other hand, since
![]() $[{\pi }_{1}^{\mathrm {t}}(U_{X_{1}}): H_{1}]=[{\pi }_{1}^{\mathrm {t}}(U_{X_{2}}): H_{2}]$
and
$[{\pi }_{1}^{\mathrm {t}}(U_{X_{1}}): H_{1}]=[{\pi }_{1}^{\mathrm {t}}(U_{X_{2}}): H_{2}]$
and
![]() $([{\pi }_{1}^{\mathrm {t}}(U_{X_{2}}): H_{2}], p)=1$
, we obtain that the natural homomorphism
$([{\pi }_{1}^{\mathrm {t}}(U_{X_{2}}): H_{2}], p)=1$
, we obtain that the natural homomorphism
![]() $\phi _{H}^{p'}: H_{1}^{p'} \twoheadrightarrow H_{2}^{p'}$
induced by
$\phi _{H}^{p'}: H_{1}^{p'} \twoheadrightarrow H_{2}^{p'}$
induced by
![]() $\phi _{H}\stackrel {\mathrm {def}}{=} \phi |_{H_{1}}: H_{1} \twoheadrightarrow H_{2}$
is also an isomorphism. This implies
$\phi _{H}\stackrel {\mathrm {def}}{=} \phi |_{H_{1}}: H_{1} \twoheadrightarrow H_{2}$
is also an isomorphism. This implies
for all
![]() $r\in \mathbb {N}$
. Let
$r\in \mathbb {N}$
. Let
![]() $K_{H_{i}, p^{r-1}}$
,
$K_{H_{i}, p^{r-1}}$
,
![]() $i\in \{1, 2\}$
, be the kernel of the natural surjection
$i\in \{1, 2\}$
, be the kernel of the natural surjection
![]() $H_{i} \twoheadrightarrow H_{i}^{\mathrm {ab}}\otimes \mathbb {Z}/(p^{r}-1)\mathbb {Z}.$
Then the surjection
$H_{i} \twoheadrightarrow H_{i}^{\mathrm {ab}}\otimes \mathbb {Z}/(p^{r}-1)\mathbb {Z}.$
Then the surjection
![]() $\phi _{H}$
implies
$\phi _{H}$
implies
 $$ \begin{align*}\text{Avr}_{p}(H_{1}) \stackrel{\mathrm{def}}{=} \lim_{r\rightarrow \infty}\frac{\text{dim}_{\mathbb{F}_{p}}(K^{\mathrm{ab}}_{H_{1}, p^{r}-1}\otimes\mathbb{F}_{p})}{\#(H_{1}^{\mathrm{ab}}\otimes \mathbb{Z}/(p^{r}-1)\mathbb{Z})}\geq \text{Avr}_{p}(H_{2}) \stackrel{\mathrm{def}}{=} \lim_{r\rightarrow \infty}\frac{\text{dim}_{\mathbb{F}_{p}}(K^{\mathrm{ab}}_{H_{2}, p^{r}-1}\otimes\mathbb{F}_{p})}{\#(H_{2}^{\mathrm{ab}}\otimes \mathbb{Z}/(p^{r}-1)\mathbb{Z})}.\end{align*} $$
$$ \begin{align*}\text{Avr}_{p}(H_{1}) \stackrel{\mathrm{def}}{=} \lim_{r\rightarrow \infty}\frac{\text{dim}_{\mathbb{F}_{p}}(K^{\mathrm{ab}}_{H_{1}, p^{r}-1}\otimes\mathbb{F}_{p})}{\#(H_{1}^{\mathrm{ab}}\otimes \mathbb{Z}/(p^{r}-1)\mathbb{Z})}\geq \text{Avr}_{p}(H_{2}) \stackrel{\mathrm{def}}{=} \lim_{r\rightarrow \infty}\frac{\text{dim}_{\mathbb{F}_{p}}(K^{\mathrm{ab}}_{H_{2}, p^{r}-1}\otimes\mathbb{F}_{p})}{\#(H_{2}^{\mathrm{ab}}\otimes \mathbb{Z}/(p^{r}-1)\mathbb{Z})}.\end{align*} $$
Thus, (ii) follows from (i).
3.4.4.
We have the following lemmas.
Lemma 3.9. Let
![]() $\ell $
be a prime number distinct from p. Then the isomorphism
$\ell $
be a prime number distinct from p. Then the isomorphism
![]() $(\phi ^{p'})^{-1}: {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})^{p'} \stackrel {\sim }{\rightarrow } {\pi }_{1}^{\mathrm {t}}(U_{X_{1}})^{p'}$
induces an isomorphism
$(\phi ^{p'})^{-1}: {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})^{p'} \stackrel {\sim }{\rightarrow } {\pi }_{1}^{\mathrm {t}}(U_{X_{1}})^{p'}$
induces an isomorphism
Proof. Let
![]() $f_{1}: (Y_{1}, D_{Y_{1}}) \rightarrow (X_{1}, D_{X_{1}})$
be an étale covering of degree
$f_{1}: (Y_{1}, D_{Y_{1}}) \rightarrow (X_{1}, D_{X_{1}})$
be an étale covering of degree
![]() $\ell $
over
$\ell $
over
![]() $k_{1}$
. Write
$k_{1}$
. Write
![]() $f_{2}: (Y_{2}, D_{Y_{2}}) \rightarrow (X_{2}, D_{X_{2}})$
for the connected Galois tame covering of degree
$f_{2}: (Y_{2}, D_{Y_{2}}) \rightarrow (X_{2}, D_{X_{2}})$
for the connected Galois tame covering of degree
![]() $\ell $
over
$\ell $
over
![]() $k_{2}$
induced by
$k_{2}$
induced by
![]() $\phi ^{p'}$
. Then we will prove that
$\phi ^{p'}$
. Then we will prove that
![]() $f_{2}$
is also an étale covering over
$f_{2}$
is also an étale covering over
![]() $k_{2}$
.
$k_{2}$
.
Write
![]() $g_{Y_{1}}$
and
$g_{Y_{1}}$
and
![]() $g_{Y_{2}}$
for the genus of
$g_{Y_{2}}$
for the genus of
![]() $Y_{1}$
and
$Y_{1}$
and
![]() $Y_{2}$
, respectively. Since
$Y_{2}$
, respectively. Since
![]() $f_{1}$
is an étale covering of degree
$f_{1}$
is an étale covering of degree
![]() $\ell $
, the Riemann-Hurwitz formula implies
$\ell $
, the Riemann-Hurwitz formula implies
![]() $g_{Y_{1}}=\ell (g_{X_{1}}-1)+1.$
On the other hand, the Riemann-Hurwitz formula implies
$g_{Y_{1}}=\ell (g_{X_{1}}-1)+1.$
On the other hand, the Riemann-Hurwitz formula implies
![]() $g_{Y_{2}}=\ell (g_{X_{2}}-1)+1+\frac {1}{2}(\ell -1)\#(\text {Ram}_{f_{2}}).$
By applying Proposition 3.8 (ii), the surjection
$g_{Y_{2}}=\ell (g_{X_{2}}-1)+1+\frac {1}{2}(\ell -1)\#(\text {Ram}_{f_{2}}).$
By applying Proposition 3.8 (ii), the surjection
![]() $\phi $
implies
$\phi $
implies
![]() $g_{Y_{1}} \geq g_{Y_{2}}.$
This means
$g_{Y_{1}} \geq g_{Y_{2}}.$
This means
![]() $\#(\text {Ram}_{f_{2}})=0.$
So
$\#(\text {Ram}_{f_{2}})=0.$
So
![]() $f_{2}$
is an étale covering over
$f_{2}$
is an étale covering over
![]() $k_{2}$
. Then the morphism
$k_{2}$
. Then the morphism
![]() $(\phi ^{p'})^{-1}$
induces an injection
$(\phi ^{p'})^{-1}$
induces an injection
Furthermore, since
![]() $\text {dim}_{\mathbb {F}_{\ell }}(\mathrm {Hom}({\pi }_{1}(X_{1}), \mathbb {F}_{\ell })) =\text {dim}_{\mathbb {F}_{\ell }}( \mathrm {Hom}({\pi }_{1}(X_{2}), \mathbb {F}_{\ell }))=2g_{X}$
, we obtain that
$\text {dim}_{\mathbb {F}_{\ell }}(\mathrm {Hom}({\pi }_{1}(X_{1}), \mathbb {F}_{\ell })) =\text {dim}_{\mathbb {F}_{\ell }}( \mathrm {Hom}({\pi }_{1}(X_{2}), \mathbb {F}_{\ell }))=2g_{X}$
, we obtain that
![]() $\psi _{X}^{\ell }$
is a bijection. This completes the proof of the lemma.
$\psi _{X}^{\ell }$
is a bijection. This completes the proof of the lemma.
Lemma 3.10. Suppose
![]() $g_{X} \geq 2$
. Then the surjection
$g_{X} \geq 2$
. Then the surjection
![]() $\phi : {\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
induces a bijection
$\phi : {\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
induces a bijection
and the bijection
![]() $\rho _{\phi }$
can be mono-anabelian reconstructed from
$\rho _{\phi }$
can be mono-anabelian reconstructed from
![]() $\phi $
.
$\phi $
.
Proof. Let
![]() $(\ell , d, y_{2})$
be an mp-triple associated to
$(\ell , d, y_{2})$
be an mp-triple associated to
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
(see Section 3.3.4). Then Lemma 3.9 implies that
${\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
(see Section 3.3.4). Then Lemma 3.9 implies that
![]() $\phi $
induces an mp-triple
$\phi $
induces an mp-triple
![]() $(\ell , d, y_{1})$
associated to
$(\ell , d, y_{1})$
associated to
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})$
, where
${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})$
, where
![]() $y_{1}\stackrel {\mathrm {def}}{=}(\psi ^{d}_{X})^{-1}(y_{2}) \in \mathrm {Hom}({\pi }_{1}(X_{1}), \mu _{d})$
.
$y_{1}\stackrel {\mathrm {def}}{=}(\psi ^{d}_{X})^{-1}(y_{2}) \in \mathrm {Hom}({\pi }_{1}(X_{1}), \mu _{d})$
.
Let
![]() $f_{i}: (Y_{i}, D_{Y_i}) \rightarrow (X_{i}, D_{X_{i}})$
,
$f_{i}: (Y_{i}, D_{Y_i}) \rightarrow (X_{i}, D_{X_{i}})$
,
![]() $i \in \{1, 2\}$
, be the étale covering of degree d over
$i \in \{1, 2\}$
, be the étale covering of degree d over
![]() $k_{i}$
induced by
$k_{i}$
induced by
![]() $y_{i}$
. Then the mp-triple
$y_{i}$
. Then the mp-triple
![]() $(\ell , d, y_{i})$
associated to
$(\ell , d, y_{i})$
associated to
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
determine an mp-triple
${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
determine an mp-triple
associated to
![]() $(X_{i}, D_{X_{i}})$
over
$(X_{i}, D_{X_{i}})$
over
![]() $k_{i}$
. Note that the types of
$k_{i}$
. Note that the types of
![]() $(Y_{1}, D_{Y_{1}})$
and
$(Y_{1}, D_{Y_{1}})$
and
![]() $(Y_{2}, D_{Y_{2}})$
are equal.
$(Y_{2}, D_{Y_{2}})$
are equal.
Write
![]() ${\pi }_{1}^{\mathrm {t}}(U_{Y_{i}})$
,
${\pi }_{1}^{\mathrm {t}}(U_{Y_{i}})$
,
![]() $i \in \{1, 2\}$
, for the kernel of
$i \in \{1, 2\}$
, for the kernel of
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{i}}) \twoheadrightarrow {\pi }_{1}(X_{i}) \overset {y_{i}}\twoheadrightarrow \mu _{d}$
. By replacing
${\pi }_{1}^{\mathrm {t}}(U_{X_{i}}) \twoheadrightarrow {\pi }_{1}(X_{i}) \overset {y_{i}}\twoheadrightarrow \mu _{d}$
. By replacing
![]() $(X_{i}, D_{X_{i}})$
by
$(X_{i}, D_{X_{i}})$
by
![]() $(Y_{i}, D_{Y_{i}})$
, Lemma 3.9 implies that
$(Y_{i}, D_{Y_{i}})$
, Lemma 3.9 implies that
![]() $(\phi |_{{\pi }_{1}^{\mathrm {t}}(U_{Y_{1}})}^{p'})^{-1}$
induces a commutative diagram as follows:
$(\phi |_{{\pi }_{1}^{\mathrm {t}}(U_{Y_{1}})}^{p'})^{-1}$
induces a commutative diagram as follows:

where all the vertical arrows are isomorphisms. We note that
![]() $H^{1}_{\text {'et}}(Y_{i}, \mathbb {F}_{\ell })$
,
$H^{1}_{\text {'et}}(Y_{i}, \mathbb {F}_{\ell })$
,
![]() $H^{1}_{\text {'et}}(U_{Y_{i}}, \mathbb {F}_{\ell })$
, and
$H^{1}_{\text {'et}}(U_{Y_{i}}, \mathbb {F}_{\ell })$
, and
![]() $\text {Div}^{0}_{D_{Y_{i}}}(Y_{i})\otimes \mathbb {F}_{\ell }$
,
$\text {Div}^{0}_{D_{Y_{i}}}(Y_{i})\otimes \mathbb {F}_{\ell }$
,
![]() $i, \in \{1, 2\}$
, are naturally isomorphic to
$i, \in \{1, 2\}$
, are naturally isomorphic to
![]() $\text {Hom}({\pi }_{1}(Y_{i}), \mathbb {F}_{\ell })$
,
$\text {Hom}({\pi }_{1}(Y_{i}), \mathbb {F}_{\ell })$
,
![]() $\text {Hom}({\pi }_{1}^{\mathrm {t}}(U_{Y_{i}}), \mathbb {F}_{\ell })$
, and
$\text {Hom}({\pi }_{1}^{\mathrm {t}}(U_{Y_{i}}), \mathbb {F}_{\ell })$
, and
![]() $\text {Hom}({\pi }_{1}^{\mathrm {t}}(U_{Y_{i}}), \mathbb {F}_{\ell })/\text {Hom}({\pi }_{1}(Y_{i}), \mathbb {F}_{\ell }),$
respectively. Then Lemma 3.5 implies that the commutative diagram above can be mono-anabelian reconstructed from
$\text {Hom}({\pi }_{1}^{\mathrm {t}}(U_{Y_{i}}), \mathbb {F}_{\ell })/\text {Hom}({\pi }_{1}(Y_{i}), \mathbb {F}_{\ell }),$
respectively. Then Lemma 3.5 implies that the commutative diagram above can be mono-anabelian reconstructed from
![]() $\phi |_{{\pi }_{1}^{\mathrm {t}}(U_{Y_{1}})}: {\pi }_{1}^{\mathrm {t}}(U_{Y_{1}}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{Y_{2}})$
.
$\phi |_{{\pi }_{1}^{\mathrm {t}}(U_{Y_{1}})}: {\pi }_{1}^{\mathrm {t}}(U_{Y_{1}}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{Y_{2}})$
.
Write
![]() $M_{Y_{i}}\subseteq M_{Y_{i}}^{*}$
for the subsets of
$M_{Y_{i}}\subseteq M_{Y_{i}}^{*}$
for the subsets of
![]() $H^{1}_{\text {'et}}(U_{Y_{i}}, \mathbb {F}_{\ell })$
defined in Section 3.2.4. Since the actions of
$H^{1}_{\text {'et}}(U_{Y_{i}}, \mathbb {F}_{\ell })$
defined in Section 3.2.4. Since the actions of
![]() $\mu _{d}$
on the exact sequences are compatible with the isomorphisms appearing in the commutative diagram above, we have
$\mu _{d}$
on the exact sequences are compatible with the isomorphisms appearing in the commutative diagram above, we have
![]() $\psi _{Y}^{\mathrm {t, \ell }}(M_{Y_{1}}^{*})=M_{Y_{2}}^{*}.$
Next, we prove
$\psi _{Y}^{\mathrm {t, \ell }}(M_{Y_{1}}^{*})=M_{Y_{2}}^{*}.$
Next, we prove
![]() $\psi _{Y}^{\mathrm {t, \ell }}(M_{Y_{1}})=M_{Y_{2}}.$
$\psi _{Y}^{\mathrm {t, \ell }}(M_{Y_{1}})=M_{Y_{2}}.$
Let
![]() $\alpha _{1} \in M_{Y_{1}}$
and
$\alpha _{1} \in M_{Y_{1}}$
and
![]() $g_{\alpha _{1}}: (Y_{\alpha _{1}}, D_{Y_{\alpha _{1}}}) \rightarrow (Y_{1}, D_{Y_{1}})$
the Galois tame covering of degree
$g_{\alpha _{1}}: (Y_{\alpha _{1}}, D_{Y_{\alpha _{1}}}) \rightarrow (Y_{1}, D_{Y_{1}})$
the Galois tame covering of degree
![]() $\ell $
over
$\ell $
over
![]() $k_{1}$
induced by
$k_{1}$
induced by
![]() $\alpha _{1}$
. Write
$\alpha _{1}$
. Write
![]() $g_{\alpha _{2}}: (Y_{\alpha _{2}}, D_{Y_{\alpha _{2}}}) \rightarrow (Y_{2}, D_{Y_{2}})$
for the Galois tame covering of degree
$g_{\alpha _{2}}: (Y_{\alpha _{2}}, D_{Y_{\alpha _{2}}}) \rightarrow (Y_{2}, D_{Y_{2}})$
for the Galois tame covering of degree
![]() $\ell $
over
$\ell $
over
![]() $k_{2}$
induced by
$k_{2}$
induced by
![]() $\alpha _{2}\stackrel {\mathrm {def}}{=}\psi ^{\mathrm {t, \ell }}_{Y}(\alpha _{1})$
. Write
$\alpha _{2}\stackrel {\mathrm {def}}{=}\psi ^{\mathrm {t, \ell }}_{Y}(\alpha _{1})$
. Write
![]() $g_{Y_{\alpha _{1}}}$
and
$g_{Y_{\alpha _{1}}}$
and
![]() $g_{Y_{\alpha _{2}}}$
for the genus of
$g_{Y_{\alpha _{2}}}$
for the genus of
![]() $Y_{\alpha _{1}}$
and
$Y_{\alpha _{1}}$
and
![]() $Y_{\alpha _{2}}$
, respectively. Then Proposition 3.8 (ii) and the Riemann-Hurwitz formula imply that
$Y_{\alpha _{2}}$
, respectively. Then Proposition 3.8 (ii) and the Riemann-Hurwitz formula imply that
![]() $g_{Y_{\alpha _{1}}}-g_{Y_{\alpha _{2}}}=\frac {1}{2}(d-\#(\text {Ram}_{g_{\alpha _{2}}}))(\ell -1)\geq 0.$
This means
$g_{Y_{\alpha _{1}}}-g_{Y_{\alpha _{2}}}=\frac {1}{2}(d-\#(\text {Ram}_{g_{\alpha _{2}}}))(\ell -1)\geq 0.$
This means
![]() $d-\#(\text {Ram}_{g_{\alpha _{2}}}) \geq 0.$
Since
$d-\#(\text {Ram}_{g_{\alpha _{2}}}) \geq 0.$
Since
![]() $\alpha _{2} \in M_{Y_{2}}^{*}$
, we have
$\alpha _{2} \in M_{Y_{2}}^{*}$
, we have
![]() $d \ | \ \#(\text {Ram}_{g_{\alpha _{2}}})$
. Thus, either
$d \ | \ \#(\text {Ram}_{g_{\alpha _{2}}})$
. Thus, either
![]() $\#(\text {Ram}_{g_{\alpha _{2}}})=0$
or
$\#(\text {Ram}_{g_{\alpha _{2}}})=0$
or
![]() $\#(\text {Ram}_{g_{\alpha _{2}}})=d$
holds.
$\#(\text {Ram}_{g_{\alpha _{2}}})=d$
holds.
If
![]() $\#(\text {Ram}_{g_{\alpha _{2}}})=0$
, then
$\#(\text {Ram}_{g_{\alpha _{2}}})=0$
, then
![]() $g_{\alpha _{2}}$
is an étale covering over
$g_{\alpha _{2}}$
is an étale covering over
![]() $k_{2}$
. Then Lemma 3.9 implies that
$k_{2}$
. Then Lemma 3.9 implies that
![]() $g_{\alpha _{1}}$
is an étale covering over
$g_{\alpha _{1}}$
is an étale covering over
![]() $k_{1}$
. This provides a contradiction to the fact that
$k_{1}$
. This provides a contradiction to the fact that
![]() $\alpha _{1} \in M_{Y_{1}}$
. Then we have
$\alpha _{1} \in M_{Y_{1}}$
. Then we have
![]() $\#(\text {Ram}_{g_{\alpha _{2}}})=d$
. This means
$\#(\text {Ram}_{g_{\alpha _{2}}})=d$
. This means
![]() $\alpha _{2} \in M_{Y_{2}}$
. Thus, we obtain
$\alpha _{2} \in M_{Y_{2}}$
. Thus, we obtain
![]() $\psi _{Y}^{\mathrm {t, \ell }}(M_{Y_{1}})\subseteq M_{Y_{2}}.$
On the other hand, Lemma 3.4 implies
$\psi _{Y}^{\mathrm {t, \ell }}(M_{Y_{1}})\subseteq M_{Y_{2}}.$
On the other hand, Lemma 3.4 implies
![]() $\#(M_{Y_{1}})=\#(M_{Y_{2}}).$
We have
$\#(M_{Y_{1}})=\#(M_{Y_{2}}).$
We have
![]() $\psi _{Y}^{\mathrm {t, \ell }}: M_{Y_{1}} \stackrel {\sim }{\rightarrow } M_{Y_{2}}.$
Then Proposition 3.3 implies that
$\psi _{Y}^{\mathrm {t, \ell }}: M_{Y_{1}} \stackrel {\sim }{\rightarrow } M_{Y_{2}}.$
Then Proposition 3.3 implies that
![]() $\psi ^{\mathrm {t, \ell }}_{Y}$
induces a bijection
$\psi ^{\mathrm {t, \ell }}_{Y}$
induces a bijection
Moreover, since
![]() $M_{Y_{i}}$
and
$M_{Y_{i}}$
and
![]() $M_{Y_{i}}^{*}$
can be mono-anabelian reconstructed from
$M_{Y_{i}}^{*}$
can be mono-anabelian reconstructed from
![]() ${\pi }_{1}^{\mathrm {t}}(U_{Y_{i}})$
, the bijection
${\pi }_{1}^{\mathrm {t}}(U_{Y_{i}})$
, the bijection
![]() $\rho _{\phi }$
can be mono-anabelian reconstructed from
$\rho _{\phi }$
can be mono-anabelian reconstructed from
![]() $\phi $
. This completes the proof of the lemma.
$\phi $
. This completes the proof of the lemma.
3.4.5.
Let
![]() $H_{2} \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
be an arbitrary open normal subgroup and
$H_{2} \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
be an arbitrary open normal subgroup and
![]() $H_{1}\stackrel {\mathrm {def}}{=}\phi ^{-1}(H_{2})$
. We write
$H_{1}\stackrel {\mathrm {def}}{=}\phi ^{-1}(H_{2})$
. We write
![]() $(X_{H_i}, D_{X_{H_i}})$
,
$(X_{H_i}, D_{X_{H_i}})$
,
![]() $i\in \{1, 2\}$
, for the smooth pointed stable curve of type
$i\in \{1, 2\}$
, for the smooth pointed stable curve of type
![]() $(g_{X_{H_{i}}}, n_{X_{H_i}})$
over
$(g_{X_{H_{i}}}, n_{X_{H_i}})$
over
![]() $k_{i}$
induced by
$k_{i}$
induced by
![]() $H_{i}$
and
$H_{i}$
and
![]() $f_{H_{i}}: (X_{H_{i}}, D_{X_{H_{i}}}) \rightarrow (X_{i}, D_{X_{i}})$
for the Galois tame coverings over
$f_{H_{i}}: (X_{H_{i}}, D_{X_{H_{i}}}) \rightarrow (X_{i}, D_{X_{i}})$
for the Galois tame coverings over
![]() $k_{i}$
induced by the inclusion
$k_{i}$
induced by the inclusion
![]() $H_{i} \hookrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
. Moreover, Proposition 3.6 implies that the inclusion
$H_{i} \hookrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
. Moreover, Proposition 3.6 implies that the inclusion
![]() $H_{i} \hookrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
induces a map
$H_{i} \hookrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
induces a map
![]() $\gamma _{H_{i}, {\pi }_{1}^{\mathrm {t}}(U_{X_{i}})}: D_{X_{H_i}}^{\mathrm {gp}} \rightarrow D_{X_{i}}^{\mathrm {gp}}$
which fits into the following commutative diagram:
$\gamma _{H_{i}, {\pi }_{1}^{\mathrm {t}}(U_{X_{i}})}: D_{X_{H_i}}^{\mathrm {gp}} \rightarrow D_{X_{i}}^{\mathrm {gp}}$
which fits into the following commutative diagram:

where
![]() $\gamma _{f_{H_{i}}}$
denotes the map of the sets of marked points induced by
$\gamma _{f_{H_{i}}}$
denotes the map of the sets of marked points induced by
![]() $f_{H_{i}}$
. We may identify
$f_{H_{i}}$
. We may identify
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})/H_{1}$
with
${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})/H_{1}$
with
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{2}})/H_{2}$
via the isomorphism
${\pi }_{1}^{\mathrm {t}}(U_{X_{2}})/H_{2}$
via the isomorphism
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})/H_{1} \stackrel {\sim }{\rightarrow } {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})/H_{2}$
induced by
${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})/H_{1} \stackrel {\sim }{\rightarrow } {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})/H_{2}$
induced by
![]() $\phi $
, and denote by
$\phi $
, and denote by
![]() $G\stackrel {\mathrm {def}}{=}{\pi }_{1}^{\mathrm {t}}(U_{X_{1}})/H_{1} \cong {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})/H_{2}$
. Then we have the following lemma.
$G\stackrel {\mathrm {def}}{=}{\pi }_{1}^{\mathrm {t}}(U_{X_{1}})/H_{1} \cong {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})/H_{2}$
. Then we have the following lemma.
Lemma 3.11. Suppose that
![]() $g_{X} \geq 2$
, and that
$g_{X} \geq 2$
, and that
![]() $(g_{X_{H_{1}}}, n_{X_{H_{1}}})=(g_{X_{H_{2}}}, n_{X_{H_{2}}})$
. Then the commutative diagram of profinite groups
$(g_{X_{H_{1}}}, n_{X_{H_{1}}})=(g_{X_{H_{2}}}, n_{X_{H_{2}}})$
. Then the commutative diagram of profinite groups

induces a commutative diagram

Moreover, the commutative diagram
![]() $(2)$
can be mono-anabelian reconstructed from
$(2)$
can be mono-anabelian reconstructed from
![]() $(1)$
.
$(1)$
.
Proof. Proposition 3.6 and Lemma 3.10 imply the diagram

can be mono-anabelian reconstructed from the commutative diagram of profinite groups

To verify Lemma 3.11, it is sufficient to check that the diagram is commutative.
Let
![]() $e^{\mathrm {gp}}_{X_{H_{1}}} \in D^{\mathrm {gp}}_{X_{H_{1}}}$
,
$e^{\mathrm {gp}}_{X_{H_{1}}} \in D^{\mathrm {gp}}_{X_{H_{1}}}$
,
![]() $e^{\mathrm {gp}}_{X_{H_{2}}}\stackrel {\mathrm {def}}{=} \rho _{\phi |_{H_{1}}}(e^{\mathrm {gp}}_{X_{H_{1}}}) \in D^{\mathrm {gp}}_{X_{H_{2}}}$
,
$e^{\mathrm {gp}}_{X_{H_{2}}}\stackrel {\mathrm {def}}{=} \rho _{\phi |_{H_{1}}}(e^{\mathrm {gp}}_{X_{H_{1}}}) \in D^{\mathrm {gp}}_{X_{H_{2}}}$
,
![]() $e^{\mathrm { gp}}_{X_1}\stackrel {\mathrm {def}}{=} \gamma _{H_{1}, {\pi }_{1}^{\mathrm {t}}(U_{X_{1}})}(e^{\mathrm {gp}}_{X_{H_{1}}}) \in D^{\mathrm {gp}}_{X_{1}}$
,
$e^{\mathrm { gp}}_{X_1}\stackrel {\mathrm {def}}{=} \gamma _{H_{1}, {\pi }_{1}^{\mathrm {t}}(U_{X_{1}})}(e^{\mathrm {gp}}_{X_{H_{1}}}) \in D^{\mathrm {gp}}_{X_{1}}$
,
![]() $e^{\mathrm {gp}}_{X_2}\stackrel {\mathrm {def}}{=} (\gamma _{H_{2}, {\pi }_{1}^{\mathrm { t}}(U_{X_{2}})}\circ \rho _{\phi |_{H_{1}}})(e^{\mathrm {gp}}_{X_{H_{1}}}) \in D^{\mathrm {gp}}_{X_{2}}$
, and
$e^{\mathrm {gp}}_{X_2}\stackrel {\mathrm {def}}{=} (\gamma _{H_{2}, {\pi }_{1}^{\mathrm { t}}(U_{X_{2}})}\circ \rho _{\phi |_{H_{1}}})(e^{\mathrm {gp}}_{X_{H_{1}}}) \in D^{\mathrm {gp}}_{X_{2}}$
, and
![]() $e^{\mathrm {gp, *}}_{X_1}\stackrel {\mathrm {def}}{=} \rho ^{-1}_{\phi }(e^{\mathrm {gp}}_{X_2}) \in D^{\mathrm {gp}}_{X_{1}}$
. Let us prove
$e^{\mathrm {gp, *}}_{X_1}\stackrel {\mathrm {def}}{=} \rho ^{-1}_{\phi }(e^{\mathrm {gp}}_{X_2}) \in D^{\mathrm {gp}}_{X_{1}}$
. Let us prove
We put
![]() $S^{\mathrm {gp}}_{X_{H_{1}}} \stackrel {\mathrm {def}}{=} \gamma _{H_{1}, {\pi }_{1}^{\mathrm {t}}(U_{X_{1}})}^{-1}(e_{X_{1}}^{\mathrm {gp, *}})$
and
$S^{\mathrm {gp}}_{X_{H_{1}}} \stackrel {\mathrm {def}}{=} \gamma _{H_{1}, {\pi }_{1}^{\mathrm {t}}(U_{X_{1}})}^{-1}(e_{X_{1}}^{\mathrm {gp, *}})$
and
![]() $S^{\mathrm { gp}}_{X_{H_{2}}}\stackrel {\mathrm {def}}{=} \gamma _{H_{2}, {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})}^{-1}(e^{\mathrm {gp}}_{X_2})$
, respectively. Note that
$S^{\mathrm { gp}}_{X_{H_{2}}}\stackrel {\mathrm {def}}{=} \gamma _{H_{2}, {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})}^{-1}(e^{\mathrm {gp}}_{X_2})$
, respectively. Note that
![]() $e^{\mathrm {gp}}_{X_{H_{2}}} \in S^{\mathrm {gp}}_{X_{H_{2}}}$
. To verify
$e^{\mathrm {gp}}_{X_{H_{2}}} \in S^{\mathrm {gp}}_{X_{H_{2}}}$
. To verify
![]() $e^{\mathrm { gp}}_{X_1}=e^{\mathrm {gp, *}}_{X_1}$
, it is sufficient to prove that
$e^{\mathrm { gp}}_{X_1}=e^{\mathrm {gp, *}}_{X_1}$
, it is sufficient to prove that
![]() $e^{\mathrm {gp}}_{X_{H_{1}}} \in S^{\mathrm {gp}}_{X_{H_{1}}}$
. Moreover, for each
$e^{\mathrm {gp}}_{X_{H_{1}}} \in S^{\mathrm {gp}}_{X_{H_{1}}}$
. Moreover, for each
![]() $i\in \{1, 2\}$
, we put
$i\in \{1, 2\}$
, we put
Then to verify the lemma, we only need to prove that
![]() $e_{X_{H_{1}}} \in {\vartheta }_{X_{H_1}}(S_{X_{H_{1}}})$
.
$e_{X_{H_{1}}} \in {\vartheta }_{X_{H_1}}(S_{X_{H_{1}}})$
.
Let
![]() $(\ell , d, y_{2})$
be an mp-triple associated to
$(\ell , d, y_{2})$
be an mp-triple associated to
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
. Then Lemma 3.9 implies that
${\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
. Then Lemma 3.9 implies that
![]() $\phi $
induces an mp-triple
$\phi $
induces an mp-triple
![]() $(\ell , d, y_{1})$
associated to
$(\ell , d, y_{1})$
associated to
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})$
, where
${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})$
, where
![]() $y_{1}\stackrel {\mathrm {def}}{=} (\psi ^{d}_{X})^{-1}(y_{2}) \in \mathrm {Hom}({\pi }_{1}(X_{1}), \mu _{d})$
. Let
$y_{1}\stackrel {\mathrm {def}}{=} (\psi ^{d}_{X})^{-1}(y_{2}) \in \mathrm {Hom}({\pi }_{1}(X_{1}), \mu _{d})$
. Let
![]() $f_{i}: (Y_{i}, D_{Y_i}) \rightarrow (X_{i}, D_{X_{i}})$
,
$f_{i}: (Y_{i}, D_{Y_i}) \rightarrow (X_{i}, D_{X_{i}})$
,
![]() $i \in \{1, 2\}$
, be the tame covering of degree d over
$i \in \{1, 2\}$
, be the tame covering of degree d over
![]() $k_{i}$
induced by
$k_{i}$
induced by
![]() $y_{i}$
. Then the mp-triple
$y_{i}$
. Then the mp-triple
![]() $(\ell , d, y_{i})$
associated to
$(\ell , d, y_{i})$
associated to
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
induces an mp-triple
${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
induces an mp-triple
associated to
![]() $(X_{i}, D_{X_{i}})$
over
$(X_{i}, D_{X_{i}})$
over
![]() $k_{i}$
. Note that since
$k_{i}$
. Note that since
![]() $f_{1}$
and
$f_{1}$
and
![]() $f_{2}$
are étale, the types of
$f_{2}$
are étale, the types of
![]() $(Y_{1}, D_{Y_{1}})$
and
$(Y_{1}, D_{Y_{1}})$
and
![]() $(Y_{2}, D_{Y_{2}})$
are equal. On the other hand, we have an mp-triple
$(Y_{2}, D_{Y_{2}})$
are equal. On the other hand, we have an mp-triple
associated to
![]() $(X_{H_2}, D_{X_{H_2}})$
induced by the natural inclusion
$(X_{H_2}, D_{X_{H_2}})$
induced by the natural inclusion
![]() $H_{2} \hookrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
and the mp-triple
$H_{2} \hookrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
and the mp-triple
![]() $(\ell , d, f_{2}: (Y_{2}, D_{Y_{2}}) \rightarrow (X_{2}, D_{X_{2}}))$
. By Lemma 3.9 again, we obtain an mp-triple
$(\ell , d, f_{2}: (Y_{2}, D_{Y_{2}}) \rightarrow (X_{2}, D_{X_{2}}))$
. By Lemma 3.9 again, we obtain an mp-triple
associated to
![]() $(X_{H_1}, D_{X_{H_1}})$
induced by
$(X_{H_1}, D_{X_{H_1}})$
induced by
![]() $\phi |_{H_{1}}$
and the triple
$\phi |_{H_{1}}$
and the triple
![]() $(\ell , d, g_{2}: (Z_{2}, D_{Z_{2}})\rightarrow (X_{H_2}, D_{X_{H_2}}))$
.
$(\ell , d, g_{2}: (Z_{2}, D_{Z_{2}})\rightarrow (X_{H_2}, D_{X_{H_2}}))$
.
Let
![]() $\alpha _{2} \in M_{Y_{2}, e_{X_2}}$
. The final paragraph of the proof of Lemma 3.10 implies that we have a bijection
$\alpha _{2} \in M_{Y_{2}, e_{X_2}}$
. The final paragraph of the proof of Lemma 3.10 implies that we have a bijection
![]() $M_{Y_{1}}=\bigsqcup _{e \in D_{X_{1}}} M_{Y_{1}, e} \stackrel {\sim }{\rightarrow } M_{Y_{2}}=\bigsqcup _{e \in D_{X_{2}}} M_{Y_{2}, e}$
induced by
$M_{Y_{1}}=\bigsqcup _{e \in D_{X_{1}}} M_{Y_{1}, e} \stackrel {\sim }{\rightarrow } M_{Y_{2}}=\bigsqcup _{e \in D_{X_{2}}} M_{Y_{2}, e}$
induced by
![]() $\phi $
. Then
$\phi $
. Then
![]() $\alpha _{2}$
induces an element
$\alpha _{2}$
induces an element
![]() $\alpha _{1} \in M_{Y_{1}, e^{*}_{X_1}}.$
Write
$\alpha _{1} \in M_{Y_{1}, e^{*}_{X_1}}.$
Write
![]() $(Y_{\alpha _{1}}, D_{Y_{\alpha _{1}}})$
and
$(Y_{\alpha _{1}}, D_{Y_{\alpha _{1}}})$
and
![]() $(Y_{\alpha _{2}}, D_{Y_{\alpha _{2}}})$
for the smooth pointed stable curves over
$(Y_{\alpha _{2}}, D_{Y_{\alpha _{2}}})$
for the smooth pointed stable curves over
![]() $k_{1}$
and
$k_{1}$
and
![]() $k_{2}$
induced by
$k_{2}$
induced by
![]() $\alpha _{1}$
and
$\alpha _{1}$
and
![]() $\alpha _{2}$
, respectively. Consider the connected Galois tame covering
$\alpha _{2}$
, respectively. Consider the connected Galois tame covering
of degree
![]() $\ell $
over
$\ell $
over
![]() $k_{2}$
, and write
$k_{2}$
, and write
![]() $\beta _{2}$
for an element of
$\beta _{2}$
for an element of
![]() $M_{Z_{2}}^{*}$
corresponding to this connected Galois tame covering. Then we have
$M_{Z_{2}}^{*}$
corresponding to this connected Galois tame covering. Then we have
 $$ \begin{align*}\beta_{2}=\sum_{c_{2}\in S_{X_{H_{2}}}} t_{c_{2}}\beta_{c_{2}},\end{align*} $$
$$ \begin{align*}\beta_{2}=\sum_{c_{2}\in S_{X_{H_{2}}}} t_{c_{2}}\beta_{c_{2}},\end{align*} $$
where
![]() $t_{c_{2}} \in (\mathbb {Z}/\ell \mathbb {Z})^{\times }$
and
$t_{c_{2}} \in (\mathbb {Z}/\ell \mathbb {Z})^{\times }$
and
![]() $\beta _{c_{2}} \in M_{Z_{2}, c_{2}}$
. On the other hand, by the proof concerning
$\beta _{c_{2}} \in M_{Z_{2}, c_{2}}$
. On the other hand, by the proof concerning
![]() $\psi _{Y}^{\mathrm {t, \ell }}(M_{Y_{1}}^{*})=M_{Y_{2}}^{*}$
in the fourth paragraph of the proof of Lemma 3.10,
$\psi _{Y}^{\mathrm {t, \ell }}(M_{Y_{1}}^{*})=M_{Y_{2}}^{*}$
in the fourth paragraph of the proof of Lemma 3.10,
![]() $\beta _{2}$
induces an element
$\beta _{2}$
induces an element
 $$ \begin{align*}\beta_{1}\stackrel{\mathrm{def}}{=} \sum_{c_{2}\in S_{X_{H_{2}}}\setminus \{e_{X_{H_{2}}}\}} t_{c_{2}}\beta_{\rho^{-1}_{\phi|_{H_{1}}}(c_{2})} +t_{e_{X_{H_{2}}}}\beta_{\rho^{-1}_{\phi|_{H_{1}}}(e_{X_{H_2}})} \\ =\sum_{c_{2}\in S_{X_{H_{2}}}\setminus \{e_{X_{H_{2}}}\}} t_{c_{2}}\beta_{\rho^{-1}_{\phi|_{H_{1}}}(c_{2})} +t_{e_{X_{H_{2}}}}\beta_{e_{X_{H_1}}}\in M_{Z_{1}}^{*}.\end{align*} $$
$$ \begin{align*}\beta_{1}\stackrel{\mathrm{def}}{=} \sum_{c_{2}\in S_{X_{H_{2}}}\setminus \{e_{X_{H_{2}}}\}} t_{c_{2}}\beta_{\rho^{-1}_{\phi|_{H_{1}}}(c_{2})} +t_{e_{X_{H_{2}}}}\beta_{\rho^{-1}_{\phi|_{H_{1}}}(e_{X_{H_2}})} \\ =\sum_{c_{2}\in S_{X_{H_{2}}}\setminus \{e_{X_{H_{2}}}\}} t_{c_{2}}\beta_{\rho^{-1}_{\phi|_{H_{1}}}(c_{2})} +t_{e_{X_{H_{2}}}}\beta_{e_{X_{H_1}}}\in M_{Z_{1}}^{*}.\end{align*} $$
Then we have that the coefficient
![]() $t_{e_{X_{H_{2}}}}$
of
$t_{e_{X_{H_{2}}}}$
of
![]() $\beta _{e_{X_{H_1}}}$
is not equal to
$\beta _{e_{X_{H_1}}}$
is not equal to
![]() $0$
. Thus, the composition
$0$
. Thus, the composition
is tamely ramified over
![]() $e_{X_{H_1}}$
. This means that
$e_{X_{H_1}}$
. This means that
![]() $e_{X_{H_{1}}}$
is contained in
$e_{X_{H_{1}}}$
is contained in
![]() $S_{X_{H_1}}$
. We complete the proof of the lemma.
$S_{X_{H_1}}$
. We complete the proof of the lemma.
Remark 3.11.1. Remark 3.6.1 implies that
![]() $D_{X_{H_i}}^{\mathrm {gp}}$
,
$D_{X_{H_i}}^{\mathrm {gp}}$
,
![]() $i\in \{1, 2\}$
, admits a natural action of G. Moreover, the commutative diagram
$i\in \{1, 2\}$
, admits a natural action of G. Moreover, the commutative diagram

is compatible with the actions of G.
3.4.6.
Next, we prove that the condition
![]() $(g_{X_{H_{1}}}, n_{X_{H_{1}}})=(g_{X_{H_{2}}}, n_{X_{H_{2}}})$
mentioned in Lemma 3.11 can be omitted. Firstly, we treat the case of abelian groups.
$(g_{X_{H_{1}}}, n_{X_{H_{1}}})=(g_{X_{H_{2}}}, n_{X_{H_{2}}})$
mentioned in Lemma 3.11 can be omitted. Firstly, we treat the case of abelian groups.
Lemma 3.12. We maintain the notation introduced in Section 3.4.5. Suppose that
![]() $g_{X}\geq 2$
, and that G is an abelian group. Then we have
$g_{X}\geq 2$
, and that G is an abelian group. Then we have
![]() $(g_{X_{H_{1}}}, n_{X_{H_{1}}})=(g_{X_{H_{2}}}, n_{X_{H_{2}}}).$
$(g_{X_{H_{1}}}, n_{X_{H_{1}}})=(g_{X_{H_{2}}}, n_{X_{H_{2}}}).$
Proof. We write m for
![]() $\#G$
and put
$\#G$
and put
![]() $K_{2}\stackrel {\mathrm {def}}{=} \text {ker}({\pi }_{1}^{\mathrm {t}}(U_{X_{2}}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})^{\mathrm {ab}}\otimes \mathbb {Z}/m\mathbb {Z}).$
Then we see immediately that
$K_{2}\stackrel {\mathrm {def}}{=} \text {ker}({\pi }_{1}^{\mathrm {t}}(U_{X_{2}}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})^{\mathrm {ab}}\otimes \mathbb {Z}/m\mathbb {Z}).$
Then we see immediately that
![]() $K_{2}$
is contained in
$K_{2}$
is contained in
![]() $H_{2}$
. Let
$H_{2}$
. Let
![]() $K_{1}\stackrel {\mathrm {def}}{=} \phi ^{-1}(K_{2}) \subseteq H_{1}$
. Write
$K_{1}\stackrel {\mathrm {def}}{=} \phi ^{-1}(K_{2}) \subseteq H_{1}$
. Write
![]() $(X_{K_{i}}, D_{X_{K_{i}}})$
for the smooth pointed stable curves of type
$(X_{K_{i}}, D_{X_{K_{i}}})$
for the smooth pointed stable curves of type
![]() $(g_{X_{K_{i}}}, n_{X_{K_{i}}})$
over
$(g_{X_{K_{i}}}, n_{X_{K_{i}}})$
over
![]() $k_{i}$
induced by
$k_{i}$
induced by
![]() $K_{i}$
and
$K_{i}$
and
![]() $f_{K_{i}}: (X_{K_{i}}, D_{X_{K_{i}}}) \rightarrow (X_{i}, D_{X_{i}})$
for the tame covering over
$f_{K_{i}}: (X_{K_{i}}, D_{X_{K_{i}}}) \rightarrow (X_{i}, D_{X_{i}})$
for the tame covering over
![]() $k_{i}$
induced by the inclusion
$k_{i}$
induced by the inclusion
![]() $K_{i}\hookrightarrow {\pi }_{1}^{\mathrm { t}}(U_{X_{i}})$
. We identify
$K_{i}\hookrightarrow {\pi }_{1}^{\mathrm { t}}(U_{X_{i}})$
. We identify
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})/K_{1}$
with
${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})/K_{1}$
with
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{2}})/K_{2}$
via the isomorphism induced by
${\pi }_{1}^{\mathrm {t}}(U_{X_{2}})/K_{2}$
via the isomorphism induced by
![]() $\phi $
, and denote by
$\phi $
, and denote by
![]() $A\stackrel {\mathrm {def}}{=} {\pi }_{1}^{\mathrm { t}}(U_{X_{1}})/K_{1} \cong {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})/K_{2}$
.
$A\stackrel {\mathrm {def}}{=} {\pi }_{1}^{\mathrm { t}}(U_{X_{1}})/K_{1} \cong {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})/K_{2}$
.
Since each p-Galois tame covering is étale (i.e., Galois tame coverings whose Galois group is a p-group), we have that
![]() $g_{X_{K_{1}}}=g_{X_{K_{2}}}$
follows from the Riemann-Hurwitz formula, and that
$g_{X_{K_{1}}}=g_{X_{K_{2}}}$
follows from the Riemann-Hurwitz formula, and that
![]() $n_{X_{K_{1}}}=\#(A)n_{X}=n_{X_{K_{2}}}$
. Then we obtain
$n_{X_{K_{1}}}=\#(A)n_{X}=n_{X_{K_{2}}}$
. Then we obtain
![]() $(g_{X_{K_{1}}}, n_{X_{K_{1}}})=(g_{X_{K_{2}}}, n_{X_{K_{2}}}).$
Thus, Lemma 3.11 implies that the commutative diagram
$(g_{X_{K_{1}}}, n_{X_{K_{1}}})=(g_{X_{K_{2}}}, n_{X_{K_{2}}}).$
Thus, Lemma 3.11 implies that the commutative diagram

of profinite groups induces a commutative diagram

Moreover, Remark 3.11.1 implies that the commutative diagram above admits a natural action of A. Then, for each
![]() $e^{\mathrm {gp}}_{X_{K_{1}}} \in D^{\mathrm {gp}}_{X_{K_{1}}}$
, the inertia subgroup
$e^{\mathrm {gp}}_{X_{K_{1}}} \in D^{\mathrm {gp}}_{X_{K_{1}}}$
, the inertia subgroup
![]() $I_{e^{\mathrm { gp}}_{X_{K_{1}}}}$
in A associated to
$I_{e^{\mathrm { gp}}_{X_{K_{1}}}}$
in A associated to
![]() $e^{\mathrm {gp}}_{X_{K_{1}}}$
(i.e., the stabilizer of
$e^{\mathrm {gp}}_{X_{K_{1}}}$
(i.e., the stabilizer of
![]() $e^{\mathrm {gp}}_{X_{K_{1}}}$
under the action of A) is equal to the inertia subgroup
$e^{\mathrm {gp}}_{X_{K_{1}}}$
under the action of A) is equal to the inertia subgroup
![]() $I_{e^{\mathrm {gp}}_{X_{K_{2}}}}$
in A associated to
$I_{e^{\mathrm {gp}}_{X_{K_{2}}}}$
in A associated to
![]() $e^{\mathrm {gp}}_{X_{K_{2}}}\stackrel {\mathrm {def}}{=} \rho _{\phi |_{K_{1}}}(e^{\mathrm {gp}}_{X_{K_{1}}}) \in D_{X_{K_{2}}}^{\mathrm {gp}}$
. On the other hand, write F for the kernel of the natural morphism
$e^{\mathrm {gp}}_{X_{K_{2}}}\stackrel {\mathrm {def}}{=} \rho _{\phi |_{K_{1}}}(e^{\mathrm {gp}}_{X_{K_{1}}}) \in D_{X_{K_{2}}}^{\mathrm {gp}}$
. On the other hand, write F for the kernel of the natural morphism
![]() $A \twoheadrightarrow G$
induced by the inclusion
$A \twoheadrightarrow G$
induced by the inclusion
![]() $K_{i} \hookrightarrow H_{i}$
,
$K_{i} \hookrightarrow H_{i}$
,
![]() $i \in \{1, 2\}.$
Since
$i \in \{1, 2\}.$
Since
![]() $(X_{H_{i}}, D_{X_{H_{i}}}) \cong (X_{K_{i}}, D_{X_{K_{i}}})/F$
, the set of ramification indices of the Galois tame covering
$(X_{H_{i}}, D_{X_{H_{i}}}) \cong (X_{K_{i}}, D_{X_{K_{i}}})/F$
, the set of ramification indices of the Galois tame covering
![]() $(X_{K_{i}}, D_{X_{K_{i}}}) \rightarrow (X_{H_{i}}, D_{X_{H_{i}}})$
with Galois group F are equal to
$(X_{K_{i}}, D_{X_{K_{i}}}) \rightarrow (X_{H_{i}}, D_{X_{H_{i}}})$
with Galois group F are equal to
![]() $\{\#(F \cap I_{e^{\mathrm {gp}}_{X_{K_{i}}}})\}_{e^{\mathrm {gp}}_{X_{K_{i}}} \in D^{\mathrm {gp}}_{X_{K_{i}}}}$
. Then, by the Riemann-Hurwitz formula, we have
$\{\#(F \cap I_{e^{\mathrm {gp}}_{X_{K_{i}}}})\}_{e^{\mathrm {gp}}_{X_{K_{i}}} \in D^{\mathrm {gp}}_{X_{K_{i}}}}$
. Then, by the Riemann-Hurwitz formula, we have
![]() $(g_{X_{H_{1}}}, n_{X_{H_{1}}})=(g_{X_{H_{2}}}, n_{X_{H_{2}}}).$
This completes the proof of the lemma.
$(g_{X_{H_{1}}}, n_{X_{H_{1}}})=(g_{X_{H_{2}}}, n_{X_{H_{2}}}).$
This completes the proof of the lemma.
Next, we treat the general case.
Lemma 3.13. We maintain the notation introduced in Section 3.4.5. Suppose that
![]() $g_{X}\geq 2$
and
$g_{X}\geq 2$
and
![]() $n_{X}\geq 2$
. Then there exists an open normal subgroup
$n_{X}\geq 2$
. Then there exists an open normal subgroup
![]() $P_{2} \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
which is contained in
$P_{2} \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
which is contained in
![]() $H_{2}$
, such that the following holds:
$H_{2}$
, such that the following holds:
Write
![]() $(X_{P_{i}}, D_{X_{P_{i}}})$
,
$(X_{P_{i}}, D_{X_{P_{i}}})$
,
![]() $i \in \{1, 2\}$
, for the smooth pointed stable curve of type
$i \in \{1, 2\}$
, for the smooth pointed stable curve of type
![]() $(g_{X_{P_{i}}}, n_{X_{P_{i}}})$
over
$(g_{X_{P_{i}}}, n_{X_{P_{i}}})$
over
![]() $k_{i}$
induced by
$k_{i}$
induced by
![]() $P_{i}$
, where
$P_{i}$
, where
![]() $P_{1}=\phi ^{-1}(P_{2})$
. We have
$P_{1}=\phi ^{-1}(P_{2})$
. We have
![]() $(g_{X_{P_{1}}}, n_{X_{P_{1}}})=(g_{X_{P_{2}}}, n_{X_{P_{2}}}).$
$(g_{X_{P_{1}}}, n_{X_{P_{1}}})=(g_{X_{P_{2}}}, n_{X_{P_{2}}}).$
Proof. First, suppose that G is a simple finite group. By applying Lemma 3.12, we may assume that G is nonabelian. Moreover, we claim that we may assume that
![]() $n_{X}$
is a positive even number. Let us prove this claim. Suppose
$n_{X}$
is a positive even number. Let us prove this claim. Suppose
![]() $p\neq 2$
. Let
$p\neq 2$
. Let
![]() $R_{2} \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
be an open subgroup, such that
$R_{2} \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
be an open subgroup, such that
![]() $\#({\pi }_{1}^{\mathrm {t}}(U_{X_{2}})/R_{2})=2$
, and that
$\#({\pi }_{1}^{\mathrm {t}}(U_{X_{2}})/R_{2})=2$
, and that
![]() $R_{2} \supseteq \text {ker}({\pi }_{1}^{\mathrm { t}}(U_{X_{2}}) \twoheadrightarrow {\pi }_{1}(X_{2}))$
(i.e., the cyclic Galois tame covering corresponding to
$R_{2} \supseteq \text {ker}({\pi }_{1}^{\mathrm { t}}(U_{X_{2}}) \twoheadrightarrow {\pi }_{1}(X_{2}))$
(i.e., the cyclic Galois tame covering corresponding to
![]() $R_{2}$
is étale). Let
$R_{2}$
is étale). Let
![]() $R_{1} \stackrel {\mathrm {def}}{=} \phi ^{-1}(R_{2}) \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{1}})$
. Then we have that
$R_{1} \stackrel {\mathrm {def}}{=} \phi ^{-1}(R_{2}) \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{1}})$
. Then we have that
![]() $\#({\pi }_{1}^{\mathrm {t}}(U_{X_{1}})/R_{1})=2$
, and that Lemma 3.9 implies
$\#({\pi }_{1}^{\mathrm {t}}(U_{X_{1}})/R_{1})=2$
, and that Lemma 3.9 implies
![]() $R_{1} \supseteq \text {ker}({\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \twoheadrightarrow {\pi }_{1}(X_{1}))$
. By replacing
$R_{1} \supseteq \text {ker}({\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \twoheadrightarrow {\pi }_{1}(X_{1}))$
. By replacing
![]() $H_{i}$
and
$H_{i}$
and
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
,
${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
,
![]() $i\in \{1, 2\}$
, by
$i\in \{1, 2\}$
, by
![]() $H_{i} \cap R_{i}$
and
$H_{i} \cap R_{i}$
and
![]() $R_{i}$
, respectively, we may assume that
$R_{i}$
, respectively, we may assume that
![]() $n_{X}$
is a positive even number. Suppose that
$n_{X}$
is a positive even number. Suppose that
![]() $p=2$
. Let
$p=2$
. Let
![]() $\ell $
be a prime number, such that
$\ell $
be a prime number, such that
![]() $(\ell , 2)=(\ell , \#G)=1$
. By [Reference RaynaudR1, Théorème 4.3.1], there exists an open subgroup
$(\ell , 2)=(\ell , \#G)=1$
. By [Reference RaynaudR1, Théorème 4.3.1], there exists an open subgroup
![]() $R^{*}_{2} \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
, such that
$R^{*}_{2} \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
, such that
![]() $\#({\pi }_{1}^{\mathrm {t}}(U_{X_{2}})/R^{*}_{2})=\ell $
, that
$\#({\pi }_{1}^{\mathrm {t}}(U_{X_{2}})/R^{*}_{2})=\ell $
, that
![]() $R^{*}_{2} \supseteq \text {ker}({\pi }_{1}^{\mathrm {t}}(U_{X_{2}}) \twoheadrightarrow {\pi }_{1}(X_{2}))$
, and that
$R^{*}_{2} \supseteq \text {ker}({\pi }_{1}^{\mathrm {t}}(U_{X_{2}}) \twoheadrightarrow {\pi }_{1}(X_{2}))$
, and that
Let
![]() $R^{*}_{1} \stackrel {\mathrm {def}}{=} \phi ^{-1}(R^{*}_{2}) \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{1}})$
. Then we have that
$R^{*}_{1} \stackrel {\mathrm {def}}{=} \phi ^{-1}(R^{*}_{2}) \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{1}})$
. Then we have that
![]() $\#({\pi }_{1}^{\mathrm {t}}(U_{X_{1}})/R^{*}_{1})=\ell $
, that
$\#({\pi }_{1}^{\mathrm {t}}(U_{X_{1}})/R^{*}_{1})=\ell $
, that
![]() $\text {dim}_{\mathbb {F}_{p}}(R_{1}^{*, \mathrm {ab}} \otimes \mathbb {F}_{p})>0$
, and that Lemma 3.9 implies
$\text {dim}_{\mathbb {F}_{p}}(R_{1}^{*, \mathrm {ab}} \otimes \mathbb {F}_{p})>0$
, and that Lemma 3.9 implies
![]() $R^{*}_{1} \supseteq \text {ker}({\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \twoheadrightarrow {\pi }_{1}(X_{1}))$
. Thus, we may take an open subgroup
$R^{*}_{1} \supseteq \text {ker}({\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \twoheadrightarrow {\pi }_{1}(X_{1}))$
. Thus, we may take an open subgroup
![]() $R^{\prime }_{2} \subseteq R^{*}_{2}$
, such that
$R^{\prime }_{2} \subseteq R^{*}_{2}$
, such that
and that
![]() $R^{\prime }_{2} \supseteq \text {ker}({\pi }_{1}^{\mathrm {t}}(U_{X_{2}}) \twoheadrightarrow {\pi }_{1}(X_{2}))$
. We put
$R^{\prime }_{2} \supseteq \text {ker}({\pi }_{1}^{\mathrm {t}}(U_{X_{2}}) \twoheadrightarrow {\pi }_{1}(X_{2}))$
. We put
![]() $R_{1}' \stackrel {\mathrm {def}}{=} \phi ^{-1}(R_{2}')$
. Then the construction of
$R_{1}' \stackrel {\mathrm {def}}{=} \phi ^{-1}(R_{2}')$
. Then the construction of
![]() $R_{1}'$
implies
$R_{1}'$
implies
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})/R^{\prime }_{1} \cong \mathbb {Z}/2\mathbb {Z} \times \mathbb {Z}/\ell \mathbb {Z}$
and
${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})/R^{\prime }_{1} \cong \mathbb {Z}/2\mathbb {Z} \times \mathbb {Z}/\ell \mathbb {Z}$
and
![]() $R^{\prime }_{1} \supseteq \text {ker}({\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \twoheadrightarrow {\pi }_{1}(X_{1}))$
. By replacing
$R^{\prime }_{1} \supseteq \text {ker}({\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \twoheadrightarrow {\pi }_{1}(X_{1}))$
. By replacing
![]() $H_{i}$
and
$H_{i}$
and
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
,
${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
,
![]() $i\in \{1, 2\}$
, by
$i\in \{1, 2\}$
, by
![]() $H_{i} \cap R^{\prime }_{i}$
and
$H_{i} \cap R^{\prime }_{i}$
and
![]() $R^{\prime }_{i}$
, respectively, we may assume that
$R^{\prime }_{i}$
, respectively, we may assume that
![]() $n_{X}$
is a positive even number. This completes the proof of the claim.
$n_{X}$
is a positive even number. This completes the proof of the claim.
Let
![]() $\#G\stackrel {\mathrm {def}}{=} p^{t}m'$
, such that
$\#G\stackrel {\mathrm {def}}{=} p^{t}m'$
, such that
![]() $(m', p)=1$
. Since
$(m', p)=1$
. Since
![]() $n_{X}$
is a positive even number, we may choose a Galois tame covering
$n_{X}$
is a positive even number, we may choose a Galois tame covering
over
![]() $k_{2}$
with Galois group
$k_{2}$
with Galois group
![]() $\mathbb {Z}/m'\mathbb {Z}$
, such that
$\mathbb {Z}/m'\mathbb {Z}$
, such that
![]() $f_{2}$
is totally ramified over every marked point of
$f_{2}$
is totally ramified over every marked point of
![]() $D_{X_{2}}$
. Write
$D_{X_{2}}$
. Write
![]() $(g_{Y_{2}}, n_{Y_{2}})$
for the type of
$(g_{Y_{2}}, n_{Y_{2}})$
for the type of
![]() $(Y_{2}, D_{Y_{2}})$
,
$(Y_{2}, D_{Y_{2}})$
,
![]() $Q_{2} \subseteq {\pi }_{1}^{\mathrm { t}}(U_{X_{2}})$
for the open normal subgroup induced by
$Q_{2} \subseteq {\pi }_{1}^{\mathrm { t}}(U_{X_{2}})$
for the open normal subgroup induced by
![]() $f_{2}$
,
$f_{2}$
,
![]() $Q_{1}\stackrel {\mathrm {def}}{=} \phi ^{-1}(Q_{2}) \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{1}})$
,
$Q_{1}\stackrel {\mathrm {def}}{=} \phi ^{-1}(Q_{2}) \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{1}})$
,
for the Galois tame covering over
![]() $k_{1}$
with Galois group
$k_{1}$
with Galois group
![]() $\mathbb {Z}/m'\mathbb {Z}$
induced by the natural inclusion
$\mathbb {Z}/m'\mathbb {Z}$
induced by the natural inclusion
![]() $Q_{1} \hookrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{1}})$
, and
$Q_{1} \hookrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{1}})$
, and
![]() $(g_{Y_{1}}, n_{Y_{1}})$
for the type of
$(g_{Y_{1}}, n_{Y_{1}})$
for the type of
![]() $(Y_{1}, D_{Y_{1}})$
. Then Lemma 3.12 implies that
$(Y_{1}, D_{Y_{1}})$
. Then Lemma 3.12 implies that
![]() $(g_{Y_{1}}, n_{Y_{1}})=(g_{Y_{2}}, n_{Y_{2}})$
and
$(g_{Y_{1}}, n_{Y_{1}})=(g_{Y_{2}}, n_{Y_{2}})$
and
![]() $f_{1}$
is also totally ramified over every marked point of
$f_{1}$
is also totally ramified over every marked point of
![]() $D_{X_{1}}$
.
$D_{X_{1}}$
.
We consider the Galois tame covering
over
![]() $k_{i}$
with Galois group
$k_{i}$
with Galois group
![]() $G \times \mathbb {Z}/m'\mathbb {Z}$
which is the composition of
$G \times \mathbb {Z}/m'\mathbb {Z}$
which is the composition of
![]() $(Z_{i}, D_{Z_{i}}) \rightarrow (Y_{i}, D_{Y_{i}})$
and
$(Z_{i}, D_{Z_{i}}) \rightarrow (Y_{i}, D_{Y_{i}})$
and
![]() $(Y_{i}, D_{Y_{i}}) \rightarrow (X_{i}, D_{X_{i}})$
. Note that since G is a nonabelian simple finite group,
$(Y_{i}, D_{Y_{i}}) \rightarrow (X_{i}, D_{X_{i}})$
. Note that since G is a nonabelian simple finite group,
![]() $(Z_{i}, D_{Z_{i}})$
is connected. Moreover, by Abhyankar’s lemma, we obtain that
$(Z_{i}, D_{Z_{i}})$
is connected. Moreover, by Abhyankar’s lemma, we obtain that
![]() $(Z_{i}, D_{Z_{i}}) \rightarrow (Y_{i}, D_{Y_{i}})$
is an étale covering over
$(Z_{i}, D_{Z_{i}}) \rightarrow (Y_{i}, D_{Y_{i}})$
is an étale covering over
![]() $k_{i}$
. Since
$k_{i}$
. Since
![]() $(g_{Y_{1}}, n_{Y_{1}})=(g_{Y_{2}}, n_{Y_{2}})$
and
$(g_{Y_{1}}, n_{Y_{1}})=(g_{Y_{2}}, n_{Y_{2}})$
and
![]() $(Z_{i}, D_{Z_{i}}) \rightarrow (Y_{i}, D_{Y_{i}})$
is unramified, the Riemann-Hurwitz formula implies
$(Z_{i}, D_{Z_{i}}) \rightarrow (Y_{i}, D_{Y_{i}})$
is unramified, the Riemann-Hurwitz formula implies
![]() $(g_{Z_{1}}, n_{Z_{1}})=(g_{Z_{2}}, n_{Z_{2}}).$
$(g_{Z_{1}}, n_{Z_{1}})=(g_{Z_{2}}, n_{Z_{2}}).$
Next, let us prove the lemma in the case where G is an arbitrary finite group. Let
![]() $G_{1} \subseteq G_{2} \subseteq \dots \subseteq G_{n}\stackrel {\mathrm {def}}{=} G$
be a sequence of subgroups of G, such that
$G_{1} \subseteq G_{2} \subseteq \dots \subseteq G_{n}\stackrel {\mathrm {def}}{=} G$
be a sequence of subgroups of G, such that
![]() $G_{i}/G_{i-1}$
is a simple group for all
$G_{i}/G_{i-1}$
is a simple group for all
![]() $i\in \{2, \dots n\}$
. In order to verify the lemma, we see that it is sufficient to prove the lemma when
$i\in \{2, \dots n\}$
. In order to verify the lemma, we see that it is sufficient to prove the lemma when
![]() $n=2$
. Let
$n=2$
. Let
![]() $N_{2}$
be the kernel of the natural homomorphism
$N_{2}$
be the kernel of the natural homomorphism
![]() ${\pi }_{1}^{\mathrm { t}}(U_{X_{2}}) \twoheadrightarrow G \twoheadrightarrow G_{1}$
and
${\pi }_{1}^{\mathrm { t}}(U_{X_{2}}) \twoheadrightarrow G \twoheadrightarrow G_{1}$
and
![]() $N_{1} \stackrel {\mathrm {def}}{=} \phi ^{-1}(N_{2})$
. Then by replacing G by
$N_{1} \stackrel {\mathrm {def}}{=} \phi ^{-1}(N_{2})$
. Then by replacing G by
![]() $G_{1}$
and by applying the lemma for the simple group
$G_{1}$
and by applying the lemma for the simple group
![]() $G_{1}$
, we obtain an open normal subgroup
$G_{1}$
, we obtain an open normal subgroup
![]() $M_{2} \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
which is contained in
$M_{2} \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
which is contained in
![]() $N_{2}$
, such that
$N_{2}$
, such that
![]() $(g_{X_{M_{1}}}, n_{X_{M_{1}}})=(g_{X_{M_{2}}}, n_{X_{M_{2}}}),$
where
$(g_{X_{M_{1}}}, n_{X_{M_{1}}})=(g_{X_{M_{2}}}, n_{X_{M_{2}}}),$
where
![]() $M_{1} \stackrel {\mathrm {def}}{=} \phi ^{-1}(M_{2})$
, and
$M_{1} \stackrel {\mathrm {def}}{=} \phi ^{-1}(M_{2})$
, and
![]() $(g_{X_{M_{i}}}, n_{X_{M_{i}}})$
,
$(g_{X_{M_{i}}}, n_{X_{M_{i}}})$
,
![]() $i\in \{1, 2\}$
, denotes the type of the smooth pointed stable curve corresponding to
$i\in \{1, 2\}$
, denotes the type of the smooth pointed stable curve corresponding to
![]() $M_{i}$
.
$M_{i}$
.
If
![]() $M_{i} \subseteq H_{i}$
,
$M_{i} \subseteq H_{i}$
,
![]() $i\in \{1, 2\}$
, then we may put
$i\in \{1, 2\}$
, then we may put
![]() $P_{i} \stackrel {\mathrm {def}}{=} M_{i}.$
If
$P_{i} \stackrel {\mathrm {def}}{=} M_{i}.$
If
![]() $H_{i}$
,
$H_{i}$
,
![]() $i\in \{1, 2\}$
, does not contain
$i\in \{1, 2\}$
, does not contain
![]() $M_{i}$
, we put
$M_{i}$
, we put
![]() $O_{i} \stackrel {\mathrm {def}}{=} M_{i} \cap H_{i}$
. Then we have
$O_{i} \stackrel {\mathrm {def}}{=} M_{i} \cap H_{i}$
. Then we have
![]() $M_{i}/O_{i}\cong G/G_{1}.$
Note that
$M_{i}/O_{i}\cong G/G_{1}.$
Note that
![]() $G/G_{1}$
is a simple group. Then the lemma follows from the lemma when we replace
$G/G_{1}$
is a simple group. Then the lemma follows from the lemma when we replace
![]() $(X_{i}, D_{X_{i}})$
and G by
$(X_{i}, D_{X_{i}})$
and G by
![]() $(X_{M_{i}}, D_{X_{M_{i}}})$
and the simple group
$(X_{M_{i}}, D_{X_{M_{i}}})$
and the simple group
![]() $G/G_{1}$
, respectively. This completes the proof of the lemma.
$G/G_{1}$
, respectively. This completes the proof of the lemma.
3.4.7.
Now, we prove the main result of the present section.
Theorem 3.14. Let
![]() $(\widetilde X_{i}, D_{\widetilde X_{i}}), i \in \{1, 2\},$
be the universal tame covering of
$(\widetilde X_{i}, D_{\widetilde X_{i}}), i \in \{1, 2\},$
be the universal tame covering of
![]() $(X_{i}, D_{X_{i}})$
defined in Section 3.1.3. Let
$(X_{i}, D_{X_{i}})$
defined in Section 3.1.3. Let
![]() $\phi : {\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
be an arbitrary open continuous surjective homomorphism. Then the group-theoretical algorithm of the mono-anabelian reconstruction concerning
$\phi : {\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
be an arbitrary open continuous surjective homomorphism. Then the group-theoretical algorithm of the mono-anabelian reconstruction concerning
![]() $\mathrm {Ine}({\pi }_{1}^{\mathrm {t}}(U_{X_{i}}))$
obtained in Proposition 3.7 is compatible with the surjection
$\mathrm {Ine}({\pi }_{1}^{\mathrm {t}}(U_{X_{i}}))$
obtained in Proposition 3.7 is compatible with the surjection
![]() $\phi : {\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
. Namely, the following holds: Let
$\phi : {\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
. Namely, the following holds: Let
![]() $\widetilde e_{2} \in D_{\widetilde X_{2}}$
and
$\widetilde e_{2} \in D_{\widetilde X_{2}}$
and
![]() $I_{\widetilde e_{2}} \in \mathrm {Ine}({\pi }_{1}^{\mathrm {t}}(U_{X_{2}}))$
the inertia subgroup associated to
$I_{\widetilde e_{2}} \in \mathrm {Ine}({\pi }_{1}^{\mathrm {t}}(U_{X_{2}}))$
the inertia subgroup associated to
![]() $\widetilde e_{2}$
. Then there exists an inertia subgroup
$\widetilde e_{2}$
. Then there exists an inertia subgroup
![]() $I_{\widetilde e_{1}} \in \mathrm {Ine}({\pi }_{1}^{\mathrm {t}}(U_{X_{1}}))$
associated to a point
$I_{\widetilde e_{1}} \in \mathrm {Ine}({\pi }_{1}^{\mathrm {t}}(U_{X_{1}}))$
associated to a point
![]() $\widetilde e_{1} \in D_{\widetilde X_{1}}$
, such that
$\widetilde e_{1} \in D_{\widetilde X_{1}}$
, such that
and that the restriction homomorphism
![]() $\phi |_{I_{\widetilde e_{1}}}: I_{\widetilde e_{1}} \twoheadrightarrow I_{\widetilde e_{2}}$
is an isomorphism.
$\phi |_{I_{\widetilde e_{1}}}: I_{\widetilde e_{1}} \twoheadrightarrow I_{\widetilde e_{2}}$
is an isomorphism.
Proof. If
![]() $n_{X}=0$
, then the theorem is trivial. We suppose
$n_{X}=0$
, then the theorem is trivial. We suppose
![]() $n_{X}>0$
. Let
$n_{X}>0$
. Let
![]() $m>>0$
be an integer number, such that
$m>>0$
be an integer number, such that
![]() $(m, p)=1$
. We put
$(m, p)=1$
. We put
![]() $K_{i}\stackrel {\mathrm {def}}{=} \text {ker}({\pi }_{1}^{\mathrm {t}}(U_{X_{i}}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{i}})^{\mathrm {ab}}\otimes \mathbb {Z}/m\mathbb {Z})$
,
$K_{i}\stackrel {\mathrm {def}}{=} \text {ker}({\pi }_{1}^{\mathrm {t}}(U_{X_{i}}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{i}})^{\mathrm {ab}}\otimes \mathbb {Z}/m\mathbb {Z})$
,
![]() $i \in \{1, 2\}$
. Write
$i \in \{1, 2\}$
. Write
![]() $(X_{K_{i}}, D_{K_{i}})$
for the smooth pointed stable curve of type
$(X_{K_{i}}, D_{K_{i}})$
for the smooth pointed stable curve of type
![]() $(g_{X_{K_{i}}}, n_{X_{K_{i}}})$
over
$(g_{X_{K_{i}}}, n_{X_{K_{i}}})$
over
![]() $k_{i}$
induced by
$k_{i}$
induced by
![]() $K_{i}$
. Moreover, the condition
$K_{i}$
. Moreover, the condition
![]() $m>>0$
implies
$m>>0$
implies
![]() $g_{X_{K_{1}}}=g_{X_{K_{2}}} \geq 2, \ n_{X_{K_{1}}}=n_{X_{K_{2}}}\geq 2.$
$g_{X_{K_{1}}}=g_{X_{K_{2}}} \geq 2, \ n_{X_{K_{1}}}=n_{X_{K_{2}}}\geq 2.$
By applying Lemma 3.13, we may choose a set of open subgroups
![]() $C_{X_{2}}\stackrel {\mathrm {def}}{=} \{H_{2, j}\}_{j \in \mathbb {Z}_{> 0}}$
of
$C_{X_{2}}\stackrel {\mathrm {def}}{=} \{H_{2, j}\}_{j \in \mathbb {Z}_{> 0}}$
of
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
, such that the following conditions hold: (a)
${\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
, such that the following conditions hold: (a)
![]() $H_{2, 1}=K_{2}$
; (b)
$H_{2, 1}=K_{2}$
; (b)
![]() $\varprojlim _{j}{\pi }_{1}^{\mathrm {t}}(U_{X_{2}})/H_{2, j} \cong {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
(i.e.,
$\varprojlim _{j}{\pi }_{1}^{\mathrm {t}}(U_{X_{2}})/H_{2, j} \cong {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
(i.e.,
![]() $C_{X_{2}}$
is a cofinal system); (c) write
$C_{X_{2}}$
is a cofinal system); (c) write
![]() $\{H_{1, j}\stackrel {\mathrm {def}}{=} \phi ^{-1}(H_{2, j})\}_{j \in \mathbb {Z}_{> 0}}$
for the set of open subgroups of
$\{H_{1, j}\stackrel {\mathrm {def}}{=} \phi ^{-1}(H_{2, j})\}_{j \in \mathbb {Z}_{> 0}}$
for the set of open subgroups of
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})$
induced by
${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})$
induced by
![]() $\phi $
, and, for each
$\phi $
, and, for each
![]() $j \in \mathbb {Z}_{> 0}$
, write
$j \in \mathbb {Z}_{> 0}$
, write
![]() $(X_{H_{i, j}}, D_{X_{H_{i, j}}})$
,
$(X_{H_{i, j}}, D_{X_{H_{i, j}}})$
,
![]() $i\in \{1, 2\}$
, for the smooth pointed stable curve of type
$i\in \{1, 2\}$
, for the smooth pointed stable curve of type
![]() $(g_{X_{H_{i,j}}}, n_{X_{H_{i,j}}})$
over
$(g_{X_{H_{i,j}}}, n_{X_{H_{i,j}}})$
over
![]() $k_{i}$
induced by
$k_{i}$
induced by
![]() $H_{i, j}$
; then we have
$H_{i, j}$
; then we have
![]() $(g_{X_{H_{1, j}}}, n_{X_{H_{1, j}}})=(g_{X_{H_{2, j}}}, n_{X_{H_{2, j}}})$
.
$(g_{X_{H_{1, j}}}, n_{X_{H_{1, j}}})=(g_{X_{H_{2, j}}}, n_{X_{H_{2, j}}})$
.
For each
![]() $j \in \mathbb {Z}_{> 0}$
, we write
$j \in \mathbb {Z}_{> 0}$
, we write
![]() $e_{X_{H_{2, j}}} \in D_{X_{H_{2, j}}}$
for the image of
$e_{X_{H_{2, j}}} \in D_{X_{H_{2, j}}}$
for the image of
![]() $\widetilde e_{2}$
. Then we obtain a sequence of marked points
$\widetilde e_{2}$
. Then we obtain a sequence of marked points
Proposition 3.6 implies that, for each
![]() $H_{2, j}$
,
$H_{2, j}$
,
![]() $j\in \mathbb {Z}_{> 0}$
, the set
$j\in \mathbb {Z}_{> 0}$
, the set
![]() $D^{\mathrm {gp}}_{X_{H_{2, j}}}$
can be mono-anabelian reconstructed from
$D^{\mathrm {gp}}_{X_{H_{2, j}}}$
can be mono-anabelian reconstructed from
![]() $H_{2, j}$
. For each
$H_{2, j}$
. For each
![]() $e_{X_{H_{2, j}}} \in D_{X_{H_{2, j}}}$
, we denote by
$e_{X_{H_{2, j}}} \in D_{X_{H_{2, j}}}$
, we denote by
Then the sequence of marked points
![]() $\mathcal {I}^{C_{X}}_{\widetilde e_{2}}$
induces a sequence
$\mathcal {I}^{C_{X}}_{\widetilde e_{2}}$
induces a sequence
Then Remark 3.6.1 implies that the inertia subgroup associated to
![]() $\widetilde e_{2}$
is equal to the stabilizer of
$\widetilde e_{2}$
is equal to the stabilizer of
![]() $\mathcal {I}^{C_{X}}_{\widetilde e_{2}^{\mathrm {gp}}}$
.
$\mathcal {I}^{C_{X}}_{\widetilde e_{2}^{\mathrm {gp}}}$
.
By Lemma 3.11 and Lemma 3.13,
![]() $\mathcal {I}_{\widetilde e^{\mathrm {gp}}_{2}}^{C_{X_{2}}}$
induces a sequence as follows:
$\mathcal {I}_{\widetilde e^{\mathrm {gp}}_{2}}^{C_{X_{2}}}$
induces a sequence as follows:
with an action of
![]() $I_{\widetilde e_{2}}$
. Then Proposition 3.7 implies that we have a sequence
$I_{\widetilde e_{2}}$
. Then Proposition 3.7 implies that we have a sequence
with an action of
![]() $I_{\widetilde e_{2}}.$
$I_{\widetilde e_{2}}.$
Let
![]() $K_{\text {ker}(\phi )}$
be the subfield of
$K_{\text {ker}(\phi )}$
be the subfield of
![]() $\widetilde K$
induced by the closed subgroup
$\widetilde K$
induced by the closed subgroup
![]() $\text {ker}(\phi )$
of
$\text {ker}(\phi )$
of
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})$
,
${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})$
,
![]() $\widetilde X_{1, \text {ker}(\phi )}$
the normalization of
$\widetilde X_{1, \text {ker}(\phi )}$
the normalization of
![]() $X_{1}$
in
$X_{1}$
in
![]() $K_{\text {ker}(\phi )}$
, and
$K_{\text {ker}(\phi )}$
, and
![]() $D_{\widetilde X_{1, \text {ker}(\phi )}}$
the inverse image of
$D_{\widetilde X_{1, \text {ker}(\phi )}}$
the inverse image of
![]() $D_{X_{1}}$
in
$D_{X_{1}}$
in
![]() $\widetilde X_{1, \text {ker}(\phi )}$
. Then the sequence
$\widetilde X_{1, \text {ker}(\phi )}$
. Then the sequence
determines a point
![]() $\widetilde e_{1, \text {ker}(\phi )} \in D_{\widetilde X_{1, \text {ker}(\phi )}}.$
We choose a point of
$\widetilde e_{1, \text {ker}(\phi )} \in D_{\widetilde X_{1, \text {ker}(\phi )}}.$
We choose a point of
![]() $\widetilde e_{1} \in D_{\widetilde X_{1}}$
, such that the image of
$\widetilde e_{1} \in D_{\widetilde X_{1}}$
, such that the image of
![]() $\widetilde e_{1}$
in
$\widetilde e_{1}$
in
![]() $D_{\widetilde X_{1, \text {ker}(\phi )}}$
is
$D_{\widetilde X_{1, \text {ker}(\phi )}}$
is
![]() $\widetilde e_{1, \text {ker}(\phi )}$
. Then we have
$\widetilde e_{1, \text {ker}(\phi )}$
. Then we have
![]() $\phi (I_{\widetilde e_{1}})=I_{\widetilde e_{2}}$
. Moreover, since
$\phi (I_{\widetilde e_{1}})=I_{\widetilde e_{2}}$
. Moreover, since
![]() $I_{\widetilde e_{1}}$
and
$I_{\widetilde e_{1}}$
and
![]() $I_{\widetilde e_{2}}$
are isomorphic to
$I_{\widetilde e_{2}}$
are isomorphic to
![]() $\widehat {\mathbb {Z}}(1)^{p'}$
, the restriction homomorphism
$\widehat {\mathbb {Z}}(1)^{p'}$
, the restriction homomorphism
![]() $\phi |_{I_{\widetilde e_{1}}}$
is an isomorphism. This completes the proof of the theorem.
$\phi |_{I_{\widetilde e_{1}}}$
is an isomorphism. This completes the proof of the theorem.
3.5. Reconstructions of additive structures via surjections
3.5.1. Settings
We maintain the settings introduced in Section 3.4.1.
3.5.2.
Let
![]() $\widetilde e_{2}$
be an arbitrary point of
$\widetilde e_{2}$
be an arbitrary point of
![]() $D_{\widetilde X_{2}}$
. By applying Theorem 3.14, there exists a point
$D_{\widetilde X_{2}}$
. By applying Theorem 3.14, there exists a point
![]() $\widetilde e_{1}\in D_{\widetilde X_{1}}$
, such that
$\widetilde e_{1}\in D_{\widetilde X_{1}}$
, such that
![]() $\phi |_{I_{\widetilde e_{1}}}: I_{\widetilde e_{1}} \stackrel {\sim }{\rightarrow } I_{\widetilde e_{2}}$
is an isomorphism. Write
$\phi |_{I_{\widetilde e_{1}}}: I_{\widetilde e_{1}} \stackrel {\sim }{\rightarrow } I_{\widetilde e_{2}}$
is an isomorphism. Write
![]() $\overline {\mathbb {F}}_{p, i}, \ i \in \{1, 2\},$
for the algebraic closure of
$\overline {\mathbb {F}}_{p, i}, \ i \in \{1, 2\},$
for the algebraic closure of
![]() $\mathbb {F}_{p}$
in
$\mathbb {F}_{p}$
in
![]() $k_{i}$
. We put
$k_{i}$
. We put
where
![]() $\{*_{\widetilde e_{i}}\}$
is an one-point set, and
$\{*_{\widetilde e_{i}}\}$
is an one-point set, and
![]() $(\mathbb {Q}/\mathbb {Z})_{i}^{p'}$
denotes the prime-to-p part of
$(\mathbb {Q}/\mathbb {Z})_{i}^{p'}$
denotes the prime-to-p part of
![]() $\mathbb {Q}/\mathbb {Z}$
which can be canonically identified with
$\mathbb {Q}/\mathbb {Z}$
which can be canonically identified with
![]() $\bigcup _{(p, m)=1}{\mathbb {\mu }}_{m}(k_{i}).$
Moreover, let
$\bigcup _{(p, m)=1}{\mathbb {\mu }}_{m}(k_{i}).$
Moreover, let
![]() $a_{\widetilde e_{i}}$
be a generator of
$a_{\widetilde e_{i}}$
be a generator of
![]() $I_{\widetilde e_{i}}$
. Then we have a natural bijection
$I_{\widetilde e_{i}}$
. Then we have a natural bijection
Thus, we obtain the following bijections
This means that
![]() $\mathbb {F}_{\widetilde e_{i}}$
can be identified with
$\mathbb {F}_{\widetilde e_{i}}$
can be identified with
![]() $\overline {\mathbb {F}}_{p, i}$
as sets, hence, admits a structure of field, whose multiplicative group is
$\overline {\mathbb {F}}_{p, i}$
as sets, hence, admits a structure of field, whose multiplicative group is
![]() $I_{\widetilde e_{i}}\otimes _{\mathbb {Z}} (\mathbb {Q}/\mathbb {Z})^{p'}_{i}$
, and whose zero element is
$I_{\widetilde e_{i}}\otimes _{\mathbb {Z}} (\mathbb {Q}/\mathbb {Z})^{p'}_{i}$
, and whose zero element is
![]() $*_{\widetilde e_{i}}$
.
$*_{\widetilde e_{i}}$
.
3.5.3.
The main goal of the present subsection is to prove that
![]() $\phi |_{I_{\widetilde e_{1}}}: I_{\widetilde e_{1}} \stackrel {\sim }{\rightarrow } I_{\widetilde e_{2}}$
induces an isomorphism
$\phi |_{I_{\widetilde e_{1}}}: I_{\widetilde e_{1}} \stackrel {\sim }{\rightarrow } I_{\widetilde e_{2}}$
induces an isomorphism
![]() $\mathbb {F}_{\widetilde e_{1}}\stackrel {\sim }{\rightarrow } \mathbb {F}_{\widetilde e_{2}}$
as fields. The main idea is as following: First, we reduce the problem to the case where
$\mathbb {F}_{\widetilde e_{1}}\stackrel {\sim }{\rightarrow } \mathbb {F}_{\widetilde e_{2}}$
as fields. The main idea is as following: First, we reduce the problem to the case where
![]() $n_{X}=3$
by applying Theorem 3.14. Second, the field structure of
$n_{X}=3$
by applying Theorem 3.14. Second, the field structure of
![]() $\mathbb {F}_{\widetilde e_{i}}$
(i.e., the set of isomorphisms of
$\mathbb {F}_{\widetilde e_{i}}$
(i.e., the set of isomorphisms of
![]() $\mathbb {F}_{\widetilde e_{i}}$
and
$\mathbb {F}_{\widetilde e_{i}}$
and
![]() $\overline {\mathbb {F}}_{p, i}$
as fields) can be translated to a certain problem concerning generalized Hasse-Witt invariants (e.g.,
$\overline {\mathbb {F}}_{p, i}$
as fields) can be translated to a certain problem concerning generalized Hasse-Witt invariants (e.g.,
![]() $\gamma _{\chi _{i}}(M_{\chi _{i}})$
in the proof of Proposition 3.15). Then by applying Theorem 3.14 again, we obtained the result by comparing
$\gamma _{\chi _{i}}(M_{\chi _{i}})$
in the proof of Proposition 3.15). Then by applying Theorem 3.14 again, we obtained the result by comparing
![]() $\gamma _{\chi _{1}}(M_{\chi _{1}})$
with
$\gamma _{\chi _{1}}(M_{\chi _{1}})$
with
![]() $\gamma _{\chi _{2}}(M_{\chi _{2}})$
.
$\gamma _{\chi _{2}}(M_{\chi _{2}})$
.
3.5.4.
We have the following proposition.
Proposition 3.15. The field structure of
![]() $\mathbb {F}_{\widetilde e_{i}}$
,
$\mathbb {F}_{\widetilde e_{i}}$
,
![]() $i\in \{1,2\}$
, can be mono-anabelian reconstructed from
$i\in \{1,2\}$
, can be mono-anabelian reconstructed from
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
. Moreover, the isomorphism
${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
. Moreover, the isomorphism
![]() $\phi |_{I_{\widetilde e_{1}}}: I_{\widetilde e_{1}} \stackrel {\sim }{\rightarrow } I_{\widetilde e_{2}}$
induces an isomorphism
$\phi |_{I_{\widetilde e_{1}}}: I_{\widetilde e_{1}} \stackrel {\sim }{\rightarrow } I_{\widetilde e_{2}}$
induces an isomorphism
as fields.
Proof. First, we claim that we may assume
![]() $n_{X}=3.$
If
$n_{X}=3.$
If
![]() $g_{X}=0$
, then
$g_{X}=0$
, then
![]() $n_{X}\geq 3$
. Suppose that
$n_{X}\geq 3$
. Suppose that
![]() $g_{X}\geq 1$
. Theorem 3.14 implies that
$g_{X}\geq 1$
. Theorem 3.14 implies that
![]() $\phi : \pi _{1}^{\mathrm {t}}(U_{X_{1}}) \twoheadrightarrow \pi _{1}^{\mathrm { t}}(U_{X_{2}})$
induces an open continuous surjection
$\phi : \pi _{1}^{\mathrm {t}}(U_{X_{1}}) \twoheadrightarrow \pi _{1}^{\mathrm { t}}(U_{X_{2}})$
induces an open continuous surjection
![]() $\phi ^{\text {'et}}: \pi _{1}(X_{1}) \twoheadrightarrow \pi _{1}(X_{2}).$
Let
$\phi ^{\text {'et}}: \pi _{1}(X_{1}) \twoheadrightarrow \pi _{1}(X_{2}).$
Let
![]() $H^{\prime }_{2} \subseteq \pi _{1}(X_{2})$
be an open normal subgroup, such that
$H^{\prime }_{2} \subseteq \pi _{1}(X_{2})$
be an open normal subgroup, such that
![]() $\#(\pi _{1}(X_{2})/H^{\prime }_{2})\geq 3$
and
$\#(\pi _{1}(X_{2})/H^{\prime }_{2})\geq 3$
and
![]() $H^{\prime }_{1} \stackrel {\mathrm {def}}{=} (\phi ^{\text {'et}})^{-1}(H_{2}')$
. Write
$H^{\prime }_{1} \stackrel {\mathrm {def}}{=} (\phi ^{\text {'et}})^{-1}(H_{2}')$
. Write
![]() $H_{i}\subseteq \pi _{1}^{\mathrm {t}}(U_{X_{i}})$
,
$H_{i}\subseteq \pi _{1}^{\mathrm {t}}(U_{X_{i}})$
,
![]() $i \in \{1, 2\}$
, for the inverse image of
$i \in \{1, 2\}$
, for the inverse image of
![]() $H_{i}'$
of the natural surjection
$H_{i}'$
of the natural surjection
![]() $\pi _{1}^{\mathrm {t}}(U_{X_{i}})\twoheadrightarrow \pi _{1}(X_{i})$
, and
$\pi _{1}^{\mathrm {t}}(U_{X_{i}})\twoheadrightarrow \pi _{1}(X_{i})$
, and
![]() $(X_{H_{i}}, D_{X_{H_i}})$
for the smooth pointed stable curve of type
$(X_{H_{i}}, D_{X_{H_i}})$
for the smooth pointed stable curve of type
![]() $(g_{X_{H_i}}, n_{X_{H_{i}}})$
over
$(g_{X_{H_i}}, n_{X_{H_{i}}})$
over
![]() $k_{i}$
induced by
$k_{i}$
induced by
![]() $H_{i}$
. Note that
$H_{i}$
. Note that
![]() $g_{X_{H_1}}=g_{X_{H_2}}\geq 2$
and
$g_{X_{H_1}}=g_{X_{H_2}}\geq 2$
and
![]() $n_{X_{H_{1}}}=n_{X_{H_{2}}}\geq 3$
. By replacing
$n_{X_{H_{1}}}=n_{X_{H_{2}}}\geq 3$
. By replacing
![]() $(X_{i}, D_{X_{i}})$
by
$(X_{i}, D_{X_{i}})$
by
![]() $(X_{H_{i}}, D_{X_{H_i}})$
, we may assume
$(X_{H_{i}}, D_{X_{H_i}})$
, we may assume
![]() $g_{X}\geq 2$
and
$g_{X}\geq 2$
and
![]() $n_{X} \geq 3$
. The surjection
$n_{X} \geq 3$
. The surjection
![]() $\phi $
induces a bijection
$\phi $
induces a bijection
 $$ \begin{align*}D_{X_{1}} \overset{\vartheta_{X_{1}}^{-1}}{\stackrel{\sim}{\rightarrow}} D_{X_{1}}^{\mathrm{gp}} \overset{\rho_{\phi}}{\stackrel{\sim}{\rightarrow}} D_{X_{2}}^{\mathrm{gp}} \overset{\vartheta_{X_{2}}}{\stackrel{\sim}{\rightarrow}} D_{X_{2}}.\end{align*} $$
$$ \begin{align*}D_{X_{1}} \overset{\vartheta_{X_{1}}^{-1}}{\stackrel{\sim}{\rightarrow}} D_{X_{1}}^{\mathrm{gp}} \overset{\rho_{\phi}}{\stackrel{\sim}{\rightarrow}} D_{X_{2}}^{\mathrm{gp}} \overset{\vartheta_{X_{2}}}{\stackrel{\sim}{\rightarrow}} D_{X_{2}}.\end{align*} $$
Let
![]() $D^{\prime }_{X_1}\stackrel {\mathrm {def}}{=} \{e_{1, 1}, e_{1, 2}, e_{1, 3}\} \subseteq D_{X_{1}}$
and
$D^{\prime }_{X_1}\stackrel {\mathrm {def}}{=} \{e_{1, 1}, e_{1, 2}, e_{1, 3}\} \subseteq D_{X_{1}}$
and
![]() $D^{\prime }_{X_2} \stackrel {\mathrm {def}}{=} \{e_{2, 1}\stackrel {\mathrm {def}}{=} \vartheta _{X_{2}}\circ \rho _{\phi }\circ \vartheta _{X_{1}}^{-1}(e_{1, 1}), e_{2, 2}\stackrel {\mathrm {def}}{=} \vartheta _{X_{2}}\circ \rho _{\phi }\circ \vartheta _{X_{1}}^{-1}(e_{1, 2}), e_{2, 3}\stackrel {\mathrm {def}}{=} \vartheta _{X_{2}}\circ \rho _{\phi }\circ \vartheta _{X_{1}}^{-1}(e_{1, 3})\} \subseteq D_{X_{2}}$
. Then
$D^{\prime }_{X_2} \stackrel {\mathrm {def}}{=} \{e_{2, 1}\stackrel {\mathrm {def}}{=} \vartheta _{X_{2}}\circ \rho _{\phi }\circ \vartheta _{X_{1}}^{-1}(e_{1, 1}), e_{2, 2}\stackrel {\mathrm {def}}{=} \vartheta _{X_{2}}\circ \rho _{\phi }\circ \vartheta _{X_{1}}^{-1}(e_{1, 2}), e_{2, 3}\stackrel {\mathrm {def}}{=} \vartheta _{X_{2}}\circ \rho _{\phi }\circ \vartheta _{X_{1}}^{-1}(e_{1, 3})\} \subseteq D_{X_{2}}$
. Then
![]() $(X_{i}, D^{\prime }_{X_i})$
,
$(X_{i}, D^{\prime }_{X_i})$
,
![]() $i\in \{1, 2\}$
, is a smooth pointed stable curve of type
$i\in \{1, 2\}$
, is a smooth pointed stable curve of type
![]() $(g_{X}, 3)$
over
$(g_{X}, 3)$
over
![]() $k_{i}$
. Write
$k_{i}$
. Write
![]() $I_{i}$
,
$I_{i}$
,
![]() $i \in \{1, 2\}$
, for the closed subgroup of
$i \in \{1, 2\}$
, for the closed subgroup of
![]() $\pi _{1}^{\mathrm {t}}(U_{X_i})$
generated by the inertia subgroups associated to the elements of
$\pi _{1}^{\mathrm {t}}(U_{X_i})$
generated by the inertia subgroups associated to the elements of
![]() $D_{\widetilde X_{i}}$
whose images in
$D_{\widetilde X_{i}}$
whose images in
![]() $D_{X_{i}}$
are contained in
$D_{X_{i}}$
are contained in
![]() $D_{X_{i}} \setminus D^{\prime }_{X_i}$
. Then we have an isomorphism
$D_{X_{i}} \setminus D^{\prime }_{X_i}$
. Then we have an isomorphism
Moreover, Theorem 3.14 implies that
![]() $\phi $
induces an open continuous surjective homomorphism
$\phi $
induces an open continuous surjective homomorphism
Thus, by replacing
![]() $(X_{i}, D_{X_{i}})$
,
$(X_{i}, D_{X_{i}})$
,
![]() $\pi _{1}^{\mathrm {t}}(U_{X_{i}})$
, and
$\pi _{1}^{\mathrm {t}}(U_{X_{i}})$
, and
![]() $\phi $
by
$\phi $
by
![]() $(X_{i}, D^{\prime }_{X_i})$
,
$(X_{i}, D^{\prime }_{X_i})$
,
![]() $\pi _{1}^{\mathrm {t}}(X_{i} \setminus D^{\prime }_{X_i})$
, and
$\pi _{1}^{\mathrm {t}}(X_{i} \setminus D^{\prime }_{X_i})$
, and
![]() $\phi '$
, respectively, we may assume
$\phi '$
, respectively, we may assume
![]() $n_{X}=3.$
$n_{X}=3.$
Let
![]() $r \in \mathbb {N}$
. We denote by
$r \in \mathbb {N}$
. We denote by
![]() $\mathbb {F}_{p^{r}, \widetilde e_{i}}, \ i \in \{1, 2\},$
the unique subfield of
$\mathbb {F}_{p^{r}, \widetilde e_{i}}, \ i \in \{1, 2\},$
the unique subfield of
![]() $\mathbb {F}_{\widetilde e_{i}}$
whose cardinality is equal to
$\mathbb {F}_{\widetilde e_{i}}$
whose cardinality is equal to
![]() $p^{r}$
. On the other hand, we fix any finite field
$p^{r}$
. On the other hand, we fix any finite field
![]() $\mathbb {F}_{p^{r}}$
of cardinality
$\mathbb {F}_{p^{r}}$
of cardinality
![]() $p^{r}$
and an algebraic closure
$p^{r}$
and an algebraic closure
![]() $\overline {\mathbb {F}}_{p}$
of
$\overline {\mathbb {F}}_{p}$
of
![]() $\mathbb {F}_{p}$
. By Proposition 3.7, we have
$\mathbb {F}_{p}$
. By Proposition 3.7, we have
![]() $\mathbb {F}_{p^{r}, \widetilde e_{i}}^{\times }=I_{\widetilde e_{i}}/(p^{r}-1)$
can be mono-anabelian reconstructed from
$\mathbb {F}_{p^{r}, \widetilde e_{i}}^{\times }=I_{\widetilde e_{i}}/(p^{r}-1)$
can be mono-anabelian reconstructed from
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
. Then reconstructing the field structure of
${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
. Then reconstructing the field structure of
![]() $\mathbb {F}_{p^{r}, \widetilde e_{i}}$
is equivalent to reconstructing
$\mathbb {F}_{p^{r}, \widetilde e_{i}}$
is equivalent to reconstructing
![]() $\text {Hom}_{\mathrm {fields}}(\mathbb {F}_{p^{r}, \widetilde e_{i}}, \mathbb {F}_{p^{r}})$
as a subset of
$\text {Hom}_{\mathrm {fields}}(\mathbb {F}_{p^{r}, \widetilde e_{i}}, \mathbb {F}_{p^{r}})$
as a subset of
![]() $\text {Hom}_{\mathrm {group}}(\mathbb {F}_{p^{r}, \widetilde e_{i}}^{\times }, \mathbb {F}_{p^{r}}^{\times })$
. Note that, in order to reconstruct the field structure of
$\text {Hom}_{\mathrm {group}}(\mathbb {F}_{p^{r}, \widetilde e_{i}}^{\times }, \mathbb {F}_{p^{r}}^{\times })$
. Note that, in order to reconstruct the field structure of
![]() $\mathbb {F}_{\widetilde e_{i}}$
, it is sufficient to reconstruct the subset
$\mathbb {F}_{\widetilde e_{i}}$
, it is sufficient to reconstruct the subset
![]() $\text {Hom}_{\mathrm {fields}}(\mathbb {F}_{p^{r}, \widetilde e_{i}}, \mathbb {F}_{p^{r}})$
for r in a cofinal subset of
$\text {Hom}_{\mathrm {fields}}(\mathbb {F}_{p^{r}, \widetilde e_{i}}, \mathbb {F}_{p^{r}})$
for r in a cofinal subset of
![]() $\mathbb {N}$
with respect to division.
$\mathbb {N}$
with respect to division.
Let
![]() $\chi _{i} \in \text {Hom}_{\mathrm {groups}}({\pi }_{1}^{\mathrm {t}}(U_{X_{i}})^{\mathrm {ab}}\otimes \mathbb {Z}/(p^{r}-1)\mathbb {Z}, \mathbb {F}^{\times }_{p^{r}}).$
Write
$\chi _{i} \in \text {Hom}_{\mathrm {groups}}({\pi }_{1}^{\mathrm {t}}(U_{X_{i}})^{\mathrm {ab}}\otimes \mathbb {Z}/(p^{r}-1)\mathbb {Z}, \mathbb {F}^{\times }_{p^{r}}).$
Write
![]() $H_{\chi _{i}}$
for the kernel of
$H_{\chi _{i}}$
for the kernel of
![]() ${\pi }_{1}^{\mathrm { t}}(U_{X_{i}}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{i}})^{\mathrm {ab}}\otimes \mathbb {Z}/(p^{r}-1)\mathbb {Z} \overset {\chi _{i}}\rightarrow \mathbb {F}_{p^{r}}^{\times }$
,
${\pi }_{1}^{\mathrm { t}}(U_{X_{i}}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{i}})^{\mathrm {ab}}\otimes \mathbb {Z}/(p^{r}-1)\mathbb {Z} \overset {\chi _{i}}\rightarrow \mathbb {F}_{p^{r}}^{\times }$
,
![]() $M_{\chi _{i}}$
for
$M_{\chi _{i}}$
for
![]() $H^{\mathrm {ab}}_{\chi _{i}} \otimes \mathbb {F}_{p}$
, and
$H^{\mathrm {ab}}_{\chi _{i}} \otimes \mathbb {F}_{p}$
, and
![]() $(X_{H_{\chi _{i}}}, D_{X_{H_{\chi _{i}}}})$
for the smooth pointed stable curve over
$(X_{H_{\chi _{i}}}, D_{X_{H_{\chi _{i}}}})$
for the smooth pointed stable curve over
![]() $k_{i}$
induced by
$k_{i}$
induced by
![]() $H_{\chi _{i}}$
. We define
$H_{\chi _{i}}$
. We define
and
![]() $\gamma _{\chi _{i}}(M_{\chi _{i}})\stackrel {\mathrm {def}}{=} \text {dim}_{\overline {\mathbb {F}}_{p}}(M_{\chi _{i}}[\chi _{i}])$
(i.e., a generalized Hasse-Witt invariant (see [Reference YangY5, Section 2.2])). Then [Reference TamagawaT4, Remark 3.7] implies
$\gamma _{\chi _{i}}(M_{\chi _{i}})\stackrel {\mathrm {def}}{=} \text {dim}_{\overline {\mathbb {F}}_{p}}(M_{\chi _{i}}[\chi _{i}])$
(i.e., a generalized Hasse-Witt invariant (see [Reference YangY5, Section 2.2])). Then [Reference TamagawaT4, Remark 3.7] implies
![]() $\gamma _{\chi _{i}}(M_{\chi _{i}}) \leq g_{X}+1$
. Moreover, we define two maps
$\gamma _{\chi _{i}}(M_{\chi _{i}}) \leq g_{X}+1$
. Moreover, we define two maps
where the map
![]() $\text {Res}_{i, r}$
is the restriction with respect to the natural inclusion
$\text {Res}_{i, r}$
is the restriction with respect to the natural inclusion
![]() $\mathbb {F}^{\times }_{p^{r}, \widetilde e_{i}} \hookrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{i}})^{\mathrm {ab}}\otimes \mathbb {Z}/(p^{r}-1)\mathbb {Z}.$
$\mathbb {F}^{\times }_{p^{r}, \widetilde e_{i}} \hookrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{i}})^{\mathrm {ab}}\otimes \mathbb {Z}/(p^{r}-1)\mathbb {Z}.$
Let
![]() $m_{0}$
be the product of all prime numbers
$m_{0}$
be the product of all prime numbers
![]() $\leq p-2$
if
$\leq p-2$
if
![]() $p\neq 2, 3$
and
$p\neq 2, 3$
and
![]() $m_{0}=1$
if
$m_{0}=1$
if
![]() $p=2, 3$
. Let
$p=2, 3$
. Let
![]() $r_{0}$
be the order of p in the multiplicative group
$r_{0}$
be the order of p in the multiplicative group
![]() $(\mathbb {Z}/m_{0}\mathbb {Z})^{\times }$
. Then [Reference TamagawaT4, Claim 5.4] implies the following result holds:
$(\mathbb {Z}/m_{0}\mathbb {Z})^{\times }$
. Then [Reference TamagawaT4, Claim 5.4] implies the following result holds:
there exists a constant
![]() $C(g_{X})$
which only depends on
$C(g_{X})$
which only depends on
![]() $g_{X}$
, such that, for each
$g_{X}$
, such that, for each
![]() $r> \text {log}_{p}(C(g_{X})+1)$
divisible by
$r> \text {log}_{p}(C(g_{X})+1)$
divisible by
![]() $r_{0}$
, we have
$r_{0}$
, we have
where
![]() $\text {Hom}^{\mathrm {surj}}_{\mathrm {groups}}(-, -)$
denotes the set of surjections whose elements are contained in
$\text {Hom}^{\mathrm {surj}}_{\mathrm {groups}}(-, -)$
denotes the set of surjections whose elements are contained in
![]() $\text {Hom}_{\mathrm {groups}}(-, -)$
.
$\text {Hom}_{\mathrm {groups}}(-, -)$
.
Let
![]() $\kappa _{2} \in \text {Hom}_{\mathrm {groups}}({\pi }_{1}^{\mathrm {t}}(U_{X_{2}})^{\mathrm {ab}}\otimes \mathbb {Z}/(p^{r}-1)\mathbb {Z}, \mathbb {F}^{\times }_{p^{r}}).$
Then
$\kappa _{2} \in \text {Hom}_{\mathrm {groups}}({\pi }_{1}^{\mathrm {t}}(U_{X_{2}})^{\mathrm {ab}}\otimes \mathbb {Z}/(p^{r}-1)\mathbb {Z}, \mathbb {F}^{\times }_{p^{r}}).$
Then
![]() $\phi $
induces a character
$\phi $
induces a character
Moreover, the surjection
![]() $\phi |_{H_{\kappa _{1}}}$
induces a surjection
$\phi |_{H_{\kappa _{1}}}$
induces a surjection
![]() $M_{\kappa _{1}}[\kappa _{1}] \twoheadrightarrow M_{\kappa _{2}}[\kappa _{2}].$
Suppose that
$M_{\kappa _{1}}[\kappa _{1}] \twoheadrightarrow M_{\kappa _{2}}[\kappa _{2}].$
Suppose that
![]() $\kappa _{2} \in \Gamma _{2, r}^{-1} (\{g_{X}+1\})$
. The surjection
$\kappa _{2} \in \Gamma _{2, r}^{-1} (\{g_{X}+1\})$
. The surjection
![]() $M_{\kappa _{1}}[\kappa _{1}] \twoheadrightarrow M_{\kappa _{2}}[\kappa _{2}]$
implies
$M_{\kappa _{1}}[\kappa _{1}] \twoheadrightarrow M_{\kappa _{2}}[\kappa _{2}]$
implies
![]() $\gamma _{\kappa _{1}}(M_{\kappa _{1}})=g_{X}+1$
. This means
$\gamma _{\kappa _{1}}(M_{\kappa _{1}})=g_{X}+1$
. This means
![]() $\kappa _{1} \in \Gamma _{1, r}^{-1} (\{g_{X}+1\})$
. On the other hand, the isomorphism
$\kappa _{1} \in \Gamma _{1, r}^{-1} (\{g_{X}+1\})$
. On the other hand, the isomorphism
![]() $\phi |_{I_{\widetilde e_{1}}}: I_{\widetilde e_{1}} \stackrel {\sim }{\rightarrow } I_{\widetilde e_{2}}$
induces an injection
$\phi |_{I_{\widetilde e_{1}}}: I_{\widetilde e_{1}} \stackrel {\sim }{\rightarrow } I_{\widetilde e_{2}}$
induces an injection
Since
![]() $\#(\text {Hom}_{\mathrm {fields}}(\mathbb {F}_{p^{r}, \widetilde e_{1}}, \mathbb {F}_{p^{r}}))=\#(\text {Hom}_{\mathrm {fields}}(\mathbb {F}_{p^{r}, \widetilde e_{2}}, \mathbb {F}_{p^{r}}))$
, we obtain that
$\#(\text {Hom}_{\mathrm {fields}}(\mathbb {F}_{p^{r}, \widetilde e_{1}}, \mathbb {F}_{p^{r}}))=\#(\text {Hom}_{\mathrm {fields}}(\mathbb {F}_{p^{r}, \widetilde e_{2}}, \mathbb {F}_{p^{r}}))$
, we obtain that
![]() $\phi |_{I_{\widetilde e_{1}}}$
induces a bijection
$\phi |_{I_{\widetilde e_{1}}}$
induces a bijection
![]() $\text {Hom}_{\mathrm {fields}}(\mathbb {F}_{p^{r}, \widetilde e_{2}}, \mathbb {F}_{p^{r}}) \stackrel {\sim }{\rightarrow } \text {Hom}_{\mathrm {fields}}(\mathbb {F}_{p^{r}, \widetilde e_{1}}, \mathbb {F}_{p^{r}}).$
Thus,
$\text {Hom}_{\mathrm {fields}}(\mathbb {F}_{p^{r}, \widetilde e_{2}}, \mathbb {F}_{p^{r}}) \stackrel {\sim }{\rightarrow } \text {Hom}_{\mathrm {fields}}(\mathbb {F}_{p^{r}, \widetilde e_{1}}, \mathbb {F}_{p^{r}}).$
Thus,
![]() $\phi |_{I_{\widetilde e_{1}}}$
induces a bijection
$\phi |_{I_{\widetilde e_{1}}}$
induces a bijection
If we choose
![]() $\overline {\mathbb {F}}_{p}=\mathbb {F}_{\widetilde e_{2}}$
, then the image of
$\overline {\mathbb {F}}_{p}=\mathbb {F}_{\widetilde e_{2}}$
, then the image of
![]() $\text {id}_{\mathbb {F}_{\widetilde e_{2}}}$
via the bijection above induces an isomorphism
$\text {id}_{\mathbb {F}_{\widetilde e_{2}}}$
via the bijection above induces an isomorphism
![]() $\theta _{\phi , \widetilde e_{1}, \widetilde e_{2}}:\mathbb {F}_{\widetilde e_{1}}\stackrel {\sim }{\rightarrow } \mathbb {F}_{\widetilde e_{2}}$
as fields. This completes the proof of the proposition.
$\theta _{\phi , \widetilde e_{1}, \widetilde e_{2}}:\mathbb {F}_{\widetilde e_{1}}\stackrel {\sim }{\rightarrow } \mathbb {F}_{\widetilde e_{2}}$
as fields. This completes the proof of the proposition.
4. Main theorems
4.1. The first main theorem
In this subsection, we apply the results obtained in previous sections to prove that the scheme-theoretical structures of curves of type
![]() $(0,n)$
over
$(0,n)$
over
![]() $\overline {\mathbb {F}}_{p}$
can be controlled group-theoretically via open continuous homomorphism (Theorem 4.3).
$\overline {\mathbb {F}}_{p}$
can be controlled group-theoretically via open continuous homomorphism (Theorem 4.3).
4.1.1. Settings
We fix some notation. Let
![]() $(X_{i}, D_{X_{i}})$
,
$(X_{i}, D_{X_{i}})$
,
![]() $i \in \{1, 2\}$
, be a smooth pointed stable curve of type
$i \in \{1, 2\}$
, be a smooth pointed stable curve of type
![]() $(g_{X}, n_{X})$
over an algebraically closed field
$(g_{X}, n_{X})$
over an algebraically closed field
![]() $k_{i}$
of characteristic
$k_{i}$
of characteristic
![]() $p>0$
,
$p>0$
,
![]() $U_{X_i}\stackrel {\mathrm {def}}{=} X_{i} \setminus D_{X_{i}}$
,
$U_{X_i}\stackrel {\mathrm {def}}{=} X_{i} \setminus D_{X_{i}}$
,
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
the tame fundamental group of
${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
the tame fundamental group of
![]() $U_{X_{i}}$
,
$U_{X_{i}}$
,
![]() ${\pi }_{1}(X_{i})$
the étale fundamental group of
${\pi }_{1}(X_{i})$
the étale fundamental group of
![]() $X_{i}$
, and
$X_{i}$
, and
![]() $(\widetilde X_{i}, D_{\widetilde X_{i}})$
the universal tame covering of
$(\widetilde X_{i}, D_{\widetilde X_{i}})$
the universal tame covering of
![]() $(X_{i}, D_{X_i})$
associated to
$(X_{i}, D_{X_i})$
associated to
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
Section (3.1.3). Let
${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
Section (3.1.3). Let
![]() $k_{i}^{\mathrm {m}}$
,
$k_{i}^{\mathrm {m}}$
,
![]() $i\in \{1, 2\}$
, be the minimal algebraically closed subfield of
$i\in \{1, 2\}$
, be the minimal algebraically closed subfield of
![]() $k_{i}$
over which
$k_{i}$
over which
![]() $U_{X_{i}}$
can be defined. Thus, by considering the function field of
$U_{X_{i}}$
can be defined. Thus, by considering the function field of
![]() $X_{i}$
, we obtain a smooth pointed stable curve
$X_{i}$
, we obtain a smooth pointed stable curve
![]() $(X^{\mathrm {m}}_{i}, D_{X^{\mathrm {m}}_{i}})$
(i.e., a minimal model of
$(X^{\mathrm {m}}_{i}, D_{X^{\mathrm {m}}_{i}})$
(i.e., a minimal model of
![]() $(X_{i}, D_{X_{i}})$
(cf. [Reference TamagawaT3, Definition 1.30 and Lemma 1.31])), such that
$(X_{i}, D_{X_{i}})$
(cf. [Reference TamagawaT3, Definition 1.30 and Lemma 1.31])), such that
![]() $U_{X_{i}} \cong U_{X^{\mathrm {m}}_{i}} \times _{k^{\mathrm {m}}_{i}}k_{i}$
as
$U_{X_{i}} \cong U_{X^{\mathrm {m}}_{i}} \times _{k^{\mathrm {m}}_{i}}k_{i}$
as
![]() $k_{i}$
-schemes, where
$k_{i}$
-schemes, where
![]() $U_{X_{i}^{\mathrm {m}}}\stackrel {\mathrm {def}}{=} X^{\mathrm {m}}_{i} \setminus D_{X_{i}^{\mathrm {m}}}.$
Note that
$U_{X_{i}^{\mathrm {m}}}\stackrel {\mathrm {def}}{=} X^{\mathrm {m}}_{i} \setminus D_{X_{i}^{\mathrm {m}}}.$
Note that
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X^{\mathrm {m}}_{i}})$
is naturally isomorphic to
${\pi }_{1}^{\mathrm {t}}(U_{X^{\mathrm {m}}_{i}})$
is naturally isomorphic to
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
. We shall denote by
${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
. We shall denote by
![]() $\overline {\mathbb {F}}_{p, i}$
the algebraic closure of
$\overline {\mathbb {F}}_{p, i}$
the algebraic closure of
![]() $\mathbb {F}_{p}$
in
$\mathbb {F}_{p}$
in
![]() $k_{i}$
. Moreover, we put
$k_{i}$
. Moreover, we put
 $$ \begin{align*} d_{(X_{i}, D_{X_{i}})}\stackrel{\mathrm{def}}{=} \left\{ \begin{array}{ll} 0, & \text{if} \ k_{i}^{\mathrm{m}} \cong \overline{\mathbb{F}}_{p, i}, \\ 1, & \text{if} \ k_{i}^{\mathrm{m}}\not\cong \overline{\mathbb{F}}_{p, i}. \end{array} \right. \end{align*} $$
$$ \begin{align*} d_{(X_{i}, D_{X_{i}})}\stackrel{\mathrm{def}}{=} \left\{ \begin{array}{ll} 0, & \text{if} \ k_{i}^{\mathrm{m}} \cong \overline{\mathbb{F}}_{p, i}, \\ 1, & \text{if} \ k_{i}^{\mathrm{m}}\not\cong \overline{\mathbb{F}}_{p, i}. \end{array} \right. \end{align*} $$
4.1.2.
Firstly, we have the following lemma.
Lemma 4.1. Let
![]() $\phi : {\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \rightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
be an arbitrary open continuous homomorphism. Then
$\phi : {\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \rightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
be an arbitrary open continuous homomorphism. Then
![]() $\phi $
is a surjection.
$\phi $
is a surjection.
Proof. We denote by
![]() $\Pi _{\phi }$
the image of
$\Pi _{\phi }$
the image of
![]() $\phi $
which is an open subgroup of
$\phi $
which is an open subgroup of
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
. Let
${\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
. Let
![]() $(X_{\phi }, D_{X_{\phi }})$
be the smooth pointed stable curve of type
$(X_{\phi }, D_{X_{\phi }})$
be the smooth pointed stable curve of type
![]() $(g_{X_{\phi }}, n_{X_{\phi }})$
over
$(g_{X_{\phi }}, n_{X_{\phi }})$
over
![]() $k_{2}$
induced by
$k_{2}$
induced by
![]() $\Pi _{\phi }$
and
$\Pi _{\phi }$
and
![]() $f_{\phi }: (X_{\phi }, D_{X_{\phi }}) \rightarrow (X_{2}, D_{X_{2}})$
the tame covering of smooth pointed stable curves over
$f_{\phi }: (X_{\phi }, D_{X_{\phi }}) \rightarrow (X_{2}, D_{X_{2}})$
the tame covering of smooth pointed stable curves over
![]() $k_{2}$
induced by the inclusion
$k_{2}$
induced by the inclusion
![]() $\Pi _{\phi } \hookrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
. Since
$\Pi _{\phi } \hookrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
. Since
![]() $f_{\phi }$
is a tame covering, we have that
$f_{\phi }$
is a tame covering, we have that
![]() $n_{X_{\phi }} \geq n_{X}$
. On the other hand, if
$n_{X_{\phi }} \geq n_{X}$
. On the other hand, if
![]() $g_{X}=0$
, we have
$g_{X}=0$
, we have
![]() $g_{\phi } \geq 0$
. If
$g_{\phi } \geq 0$
. If
![]() $g_{X}>0$
, the Riemann-Hurwitz formula implies
$g_{X}>0$
, the Riemann-Hurwitz formula implies
![]() $g_{X_{\phi }}\geq [{\pi }_{1}^{\mathrm {t}}(U_{X_{2}}): \Pi _{\phi }](g_{X}-1)+1\geq g_{X}$
. Then we have
$g_{X_{\phi }}\geq [{\pi }_{1}^{\mathrm {t}}(U_{X_{2}}): \Pi _{\phi }](g_{X}-1)+1\geq g_{X}$
. Then we have
![]() $g_{\phi }\geq g_{X}$
and
$g_{\phi }\geq g_{X}$
and
![]() $n_{X_{\phi }}\geq n_{X}$
. Note that
$n_{X_{\phi }}\geq n_{X}$
. Note that
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \twoheadrightarrow \Pi _{\phi } \hookrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
implies
${\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \twoheadrightarrow \Pi _{\phi } \hookrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
implies
Then we obtain that
![]() $2g_{X}+n_{X}-1=2g_{X_{\phi }}+n_{X_{\phi }}-1$
. Moreover, Proposition 3.8 (ii) and the natural surjection
$2g_{X}+n_{X}-1=2g_{X_{\phi }}+n_{X_{\phi }}-1$
. Moreover, Proposition 3.8 (ii) and the natural surjection
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \twoheadrightarrow \Pi _{\phi }$
induced by
${\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \twoheadrightarrow \Pi _{\phi }$
induced by
![]() $\phi $
imply that
$\phi $
imply that
![]() $g_{X}\geq g_{X_{\phi }}$
. Then we obtain that
$g_{X}\geq g_{X_{\phi }}$
. Then we obtain that
![]() $g_{X}=g_{X_{\phi }}.$
Thus, we have
$g_{X}=g_{X_{\phi }}.$
Thus, we have
![]() $(g_{X}, n_{X})=(g_{X_{\phi }}, n_{X_{\phi }}).$
This means that the tame covering
$(g_{X}, n_{X})=(g_{X_{\phi }}, n_{X_{\phi }}).$
This means that the tame covering
![]() $f_{\phi }: (X_{\phi }, D_{X_{\phi }}) \rightarrow (X_{2}, D_{X_{2}})$
is totally ramified over every marked point of
$f_{\phi }: (X_{\phi }, D_{X_{\phi }}) \rightarrow (X_{2}, D_{X_{2}})$
is totally ramified over every marked point of
![]() $D_{X_{2}}$
.
$D_{X_{2}}$
.
Let us prove
![]() $[{\pi }_{1}^{\mathrm {t}}(U_{X_{2}}): \Pi _{\phi }]=1$
. Suppose
$[{\pi }_{1}^{\mathrm {t}}(U_{X_{2}}): \Pi _{\phi }]=1$
. Suppose
![]() $[{\pi }_{1}^{\mathrm {t}}(U_{X_{2}}): \Pi _{\phi }]\neq 1$
. Since
$[{\pi }_{1}^{\mathrm {t}}(U_{X_{2}}): \Pi _{\phi }]\neq 1$
. Since
![]() $f_{\phi }$
is totally ramified, the Riemann-Hurwitz formula implies
$f_{\phi }$
is totally ramified, the Riemann-Hurwitz formula implies
![]() $g_{X_{\phi }}>g_{X}$
if
$g_{X_{\phi }}>g_{X}$
if
![]() $n_{X} \neq 0$
and
$n_{X} \neq 0$
and
![]() $g_{X}\neq 0$
. This is a contradiction. If
$g_{X}\neq 0$
. This is a contradiction. If
![]() $n_{X}=0$
, the Riemann-Hurwitz formula implies
$n_{X}=0$
, the Riemann-Hurwitz formula implies
![]() $g_{X}=1$
if
$g_{X}=1$
if
![]() $g_{X}\neq 0$
. This contradicts the assumption where
$g_{X}\neq 0$
. This contradicts the assumption where
![]() $(X_{i}, D_{X_{i}})$
is a pointed stable curve. Then we obtain
$(X_{i}, D_{X_{i}})$
is a pointed stable curve. Then we obtain
![]() $g_{X}=g_{X_{\phi }}=0$
. Moreover, by applying the Riemann-Hurwitz formula again, since
$g_{X}=g_{X_{\phi }}=0$
. Moreover, by applying the Riemann-Hurwitz formula again, since
![]() $n_{X}=n_{X_{\phi }}$
, we obtain
$n_{X}=n_{X_{\phi }}$
, we obtain
![]() $n_{X}=n_{X_{\phi }}=2$
. This contradicts the assumption where
$n_{X}=n_{X_{\phi }}=2$
. This contradicts the assumption where
![]() $(X_{i}, D_{X_{i}})$
is a pointed stable curve. Then we have
$(X_{i}, D_{X_{i}})$
is a pointed stable curve. Then we have
![]() $[{\pi }_{1}^{\mathrm {t}}(U_{X_{2}}): \Pi _{\phi }]=1$
. This means that
$[{\pi }_{1}^{\mathrm {t}}(U_{X_{2}}): \Pi _{\phi }]=1$
. This means that
![]() $\phi $
is a surjection.
$\phi $
is a surjection.
4.1.3. Further settings
In the remainder of this subsection, we suppose
![]() $(g_{X}, n_{X})=(0, n)$
. We fix two marked points
$(g_{X}, n_{X})=(0, n)$
. We fix two marked points
![]() $e_{1, \infty }, e_{1, 0} \in D_{X_{1}}$
distinct from each other. Moreover, we choose any field
$e_{1, \infty }, e_{1, 0} \in D_{X_{1}}$
distinct from each other. Moreover, we choose any field
![]() $k_{1}'\cong k_{1}$
, and choose any isomorphism
$k_{1}'\cong k_{1}$
, and choose any isomorphism
![]() $\varphi _{1}: X_{1} \stackrel {\sim }{\rightarrow } \mathbb {P}_{k_{1}'}^{1}$
as schemes, such that
$\varphi _{1}: X_{1} \stackrel {\sim }{\rightarrow } \mathbb {P}_{k_{1}'}^{1}$
as schemes, such that
![]() $\varphi _{1}(e_{1, \infty })=\infty $
and
$\varphi _{1}(e_{1, \infty })=\infty $
and
![]() $\varphi _{1}(e_{1, 0})=0$
. Then the set of
$\varphi _{1}(e_{1, 0})=0$
. Then the set of
![]() $k_{1}$
-rational points
$k_{1}$
-rational points
![]() $X_{1}(k_{1}) \setminus \{e_{1, \infty }\}$
is equipped with a structure of
$X_{1}(k_{1}) \setminus \{e_{1, \infty }\}$
is equipped with a structure of
![]() $\mathbb {F}_{p}$
-module via the bijection
$\mathbb {F}_{p}$
-module via the bijection
![]() $\varphi _{1}$
. Note that since any
$\varphi _{1}$
. Note that since any
![]() $k_{1}'$
-isomorphism of
$k_{1}'$
-isomorphism of
![]() $\mathbb {P}_{k_{1}'}^{1}$
fixing
$\mathbb {P}_{k_{1}'}^{1}$
fixing
![]() $\infty $
and
$\infty $
and
![]() $0$
is a scalar multiplication, the
$0$
is a scalar multiplication, the
![]() $\mathbb {F}_{p}$
-module structure of
$\mathbb {F}_{p}$
-module structure of
![]() $X_{1}(k_{1}) \setminus \{e_{1, \infty }\}$
does not depend on the choices of
$X_{1}(k_{1}) \setminus \{e_{1, \infty }\}$
does not depend on the choices of
![]() $k^{\prime }_{1}$
and
$k^{\prime }_{1}$
and
![]() $\varphi _{1}$
but depends only on the choices of
$\varphi _{1}$
but depends only on the choices of
![]() $e_{1, \infty }$
and
$e_{1, \infty }$
and
![]() $ e_{1, 0}$
. Then we shall say that
$ e_{1, 0}$
. Then we shall say that
![]() $X_{1}(k_{1}) \setminus \{e_{1, \infty }\}$
is equipped with a structure of
$X_{1}(k_{1}) \setminus \{e_{1, \infty }\}$
is equipped with a structure of
![]() $\mathbb {F}_{p}$
-module with respect to
$\mathbb {F}_{p}$
-module with respect to
![]() $e_{1, \infty }$
and
$e_{1, \infty }$
and
![]() $e_{1, 0}$
.
$e_{1, 0}$
.
By applying Theorem 3.14, in the next lemma, we will prove that Tamagawa’s group-theoretical criterion (i.e. [Reference TamagawaT2, Lemma 3.3]) for linear conditions is compatible with arbitrary open continuous surjective homomorphism.
Lemma 4.2. Let
![]() $\phi : {\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
be an open continuous surjective homomorphism. By Lemma 3.10,
$\phi : {\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
be an open continuous surjective homomorphism. By Lemma 3.10,
![]() $\phi $
induces a bijection
$\phi $
induces a bijection
![]() $\rho _{\phi }: D^{\mathrm {gp}}_{X_{1}} \stackrel {\sim }{\rightarrow } D^{\mathrm {gp}}_{X_{2}}$
. We may identify
$\rho _{\phi }: D^{\mathrm {gp}}_{X_{1}} \stackrel {\sim }{\rightarrow } D^{\mathrm {gp}}_{X_{2}}$
. We may identify
![]() $D^{\mathrm {gp}}_{X_{i}}, i\in \{1, 2\}$
, with
$D^{\mathrm {gp}}_{X_{i}}, i\in \{1, 2\}$
, with
![]() $D_{X_{i}}$
via the bijection
$D_{X_{i}}$
via the bijection
![]() ${\vartheta }_{X_{i}}: D_{X_{i}}^{\mathrm {gp}} \stackrel {\sim }{\rightarrow } D_{X_{i}}$
. Write
${\vartheta }_{X_{i}}: D_{X_{i}}^{\mathrm {gp}} \stackrel {\sim }{\rightarrow } D_{X_{i}}$
. Write
![]() $e_{2, \infty }$
and
$e_{2, \infty }$
and
![]() $e_{2, 0}$
for
$e_{2, 0}$
for
![]() $\rho _{\phi }(e_{1, \infty })$
and
$\rho _{\phi }(e_{1, \infty })$
and
![]() $\rho _{\phi }(e_{1, 0})$
, respectively. Let
$\rho _{\phi }(e_{1, 0})$
, respectively. Let
 $$ \begin{align*}\sum_{e_{1}\in D_{X_{1}}\setminus \{e_{1, \infty}, e_{1, 0}\}}b_{e_{1}}e_{1}=e_{1, 0}\end{align*} $$
$$ \begin{align*}\sum_{e_{1}\in D_{X_{1}}\setminus \{e_{1, \infty}, e_{1, 0}\}}b_{e_{1}}e_{1}=e_{1, 0}\end{align*} $$
be a linear condition with respect to
![]() $e_{1, \infty }$
and
$e_{1, \infty }$
and
![]() $e_{1, 0}$
on
$e_{1, 0}$
on
![]() $(X_{1}, D_{X_{1}})$
, where
$(X_{1}, D_{X_{1}})$
, where
![]() $b_{e_{1}} \in \mathbb {F}_{p}$
for each
$b_{e_{1}} \in \mathbb {F}_{p}$
for each
![]() $e_{1}\in D_{X_{1}}\setminus \{e_{1, \infty }, e_{1, 0}\}$
. Then the linear condition
$e_{1}\in D_{X_{1}}\setminus \{e_{1, \infty }, e_{1, 0}\}$
. Then the linear condition
 $$ \begin{align*}\sum_{e_{1}\in D_{X_{1}}\setminus \{e_{1, \infty}, e_{1, 0}\}}b_{e_{1}}\rho_{\phi}(e_{1})=\rho_{\phi}(e_{1, 0})=e_{2, 0}\end{align*} $$
$$ \begin{align*}\sum_{e_{1}\in D_{X_{1}}\setminus \{e_{1, \infty}, e_{1, 0}\}}b_{e_{1}}\rho_{\phi}(e_{1})=\rho_{\phi}(e_{1, 0})=e_{2, 0}\end{align*} $$
with respect to
![]() $e_{2, \infty }$
and
$e_{2, \infty }$
and
![]() $e_{2, 0}$
on
$e_{2, 0}$
on
![]() $(X_{2}, D_{X_{2}})$
also holds.
$(X_{2}, D_{X_{2}})$
also holds.
Proof. Let
![]() $\widetilde e_{2, \infty } \in D_{\widetilde X_{2}}$
be a point over
$\widetilde e_{2, \infty } \in D_{\widetilde X_{2}}$
be a point over
![]() $e_{2, \infty }$
. The set
$e_{2, \infty }$
. The set
![]() $\mathbb {F}_{\widetilde e_{2, \infty }}\stackrel {\mathrm {def}}{=} (I_{\widetilde e_{2, \infty }}\otimes _{\mathbb {Z}} (\mathbb {Q}/\mathbb {Z})^{p'}_{2}) \sqcup \{*_{\widetilde e_{2, \infty }}\}$
admits a structure of field, and Proposition 3.15 implies that the field structure can be mono-anabelian reconstructed from
$\mathbb {F}_{\widetilde e_{2, \infty }}\stackrel {\mathrm {def}}{=} (I_{\widetilde e_{2, \infty }}\otimes _{\mathbb {Z}} (\mathbb {Q}/\mathbb {Z})^{p'}_{2}) \sqcup \{*_{\widetilde e_{2, \infty }}\}$
admits a structure of field, and Proposition 3.15 implies that the field structure can be mono-anabelian reconstructed from
![]() ${\pi }_{1}^{\mathrm { t}}(U_{X_{2}})$
. Theorem 3.14 implies that there exists a point
${\pi }_{1}^{\mathrm { t}}(U_{X_{2}})$
. Theorem 3.14 implies that there exists a point
![]() $\widetilde e_{1, \infty } \in D_{\widetilde X_{1}}$
over
$\widetilde e_{1, \infty } \in D_{\widetilde X_{1}}$
over
![]() $e_{1, \infty }$
, such that
$e_{1, \infty }$
, such that
![]() $\phi (I_{\widetilde e_{1, \infty }})=\widetilde e_{2, \infty }$
. By Proposition 3.15 again, the set
$\phi (I_{\widetilde e_{1, \infty }})=\widetilde e_{2, \infty }$
. By Proposition 3.15 again, the set
![]() $\mathbb {F}_{\widetilde e_{1, \infty }}\stackrel {\mathrm {def}}{=} (I_{\widetilde e_{1, \infty }}\otimes _{\mathbb {Z}} (\mathbb {Q}/\mathbb {Z})^{p'}_{1}) \sqcup \{*_{\widetilde e_{1, \infty }}\}$
admits a structure of field which can be mono-anabelian reconstructed from
$\mathbb {F}_{\widetilde e_{1, \infty }}\stackrel {\mathrm {def}}{=} (I_{\widetilde e_{1, \infty }}\otimes _{\mathbb {Z}} (\mathbb {Q}/\mathbb {Z})^{p'}_{1}) \sqcup \{*_{\widetilde e_{1, \infty }}\}$
admits a structure of field which can be mono-anabelian reconstructed from
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})$
, and
${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})$
, and
![]() $\phi $
induces an isomorphism
$\phi $
induces an isomorphism
![]() $\theta _{\phi , \widetilde e_{1, \infty }, \widetilde e_{2, \infty }}: \mathbb {F}_{\widetilde e_{1, \infty }} \stackrel {\sim }{\rightarrow } \mathbb {F}_{\widetilde e_{2, \infty }}$
as fields.
$\theta _{\phi , \widetilde e_{1, \infty }, \widetilde e_{2, \infty }}: \mathbb {F}_{\widetilde e_{1, \infty }} \stackrel {\sim }{\rightarrow } \mathbb {F}_{\widetilde e_{2, \infty }}$
as fields.
For each
![]() $e_{1} \in D_{X_{1}}$
, we take
$e_{1} \in D_{X_{1}}$
, we take
![]() $b^{\prime }_{e_{1}} \in \mathbb {Z}_{\geq 0}$
, such that
$b^{\prime }_{e_{1}} \in \mathbb {Z}_{\geq 0}$
, such that
![]() $b^{\prime }_{e_{1}} \equiv b_{e_{1}} \ (\text {mod} \ p)$
and
$b^{\prime }_{e_{1}} \equiv b_{e_{1}} \ (\text {mod} \ p)$
and
 $$ \begin{align*}\sum_{e_{1}\in D_{X_{1}}\setminus \{e_{1, \infty}, e_{1, 0}\}}b^{\prime}_{e_{1}} \geq 2.\end{align*} $$
$$ \begin{align*}\sum_{e_{1}\in D_{X_{1}}\setminus \{e_{1, \infty}, e_{1, 0}\}}b^{\prime}_{e_{1}} \geq 2.\end{align*} $$
Let
![]() $r \geq 1$
, such that
$r \geq 1$
, such that
![]() $p^{r}-2 \geq \sum _{e_{1}\in D_{X_{1}}\setminus \{e_{1, \infty }, e_{1, 0}\}}b^{\prime }_{e_{1}}.$
For each
$p^{r}-2 \geq \sum _{e_{1}\in D_{X_{1}}\setminus \{e_{1, \infty }, e_{1, 0}\}}b^{\prime }_{e_{1}}.$
For each
![]() $\widetilde e_{1} \in D_{\widetilde {X}_{1}}$
over
$\widetilde e_{1} \in D_{\widetilde {X}_{1}}$
over
![]() $e_{1}$
, write
$e_{1}$
, write
![]() $I_{\widetilde {e}_{1}, \mathrm {ab}}$
for the image of the natural morphism
$I_{\widetilde {e}_{1}, \mathrm {ab}}$
for the image of the natural morphism
![]() $I_{\widetilde {e}_{1}} \hookrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{1}})^{\mathrm {ab}}.$
Moreover, since the image of
$I_{\widetilde {e}_{1}} \hookrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{1}})^{\mathrm {ab}}.$
Moreover, since the image of
![]() $I_{\widetilde {e}_{1}, \mathrm {ab}}$
does not depend on the choices of
$I_{\widetilde {e}_{1}, \mathrm {ab}}$
does not depend on the choices of
![]() $\widetilde {e}_{1}$
, we may write
$\widetilde {e}_{1}$
, we may write
![]() $I_{e_{1}}$
for
$I_{e_{1}}$
for
![]() $I_{\widetilde {e}_{1}, \mathrm {ab}}$
. The structure of the maximal prime-to-p quotient of
$I_{\widetilde {e}_{1}, \mathrm {ab}}$
. The structure of the maximal prime-to-p quotient of
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})$
implies that
${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})$
implies that
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})^{\mathrm {ab}}$
is generated by
${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})^{\mathrm {ab}}$
is generated by
![]() $\{I_{e_{1}}\}_{e_{1} \in D_{X_{1}}}$
, and that there exists a generator
$\{I_{e_{1}}\}_{e_{1} \in D_{X_{1}}}$
, and that there exists a generator
![]() $a_{e_{1}}$
,
$a_{e_{1}}$
,
![]() $e_{1} \in D_{X_{1}}$
, of
$e_{1} \in D_{X_{1}}$
, of
![]() $I_{e_{1}}$
, such that
$I_{e_{1}}$
, such that
![]() $\prod _{e_{1} \in D_{X_{1}}}a_{e_{1}}=1.$
We define
$\prod _{e_{1} \in D_{X_{1}}}a_{e_{1}}=1.$
We define
 $$ \begin{align*}\ I_{e_{1, 0}} \rightarrow \mathbb{Z}/(p^{r}-1)\mathbb{Z}, \ a_{e_{1, 0}} \mapsto (\sum_{e_{1}\in D_{X_{1}}\setminus \{e_{1, \infty}, e_{1, 0}\}}b^{\prime}_{e_{1}})-1,\end{align*} $$
$$ \begin{align*}\ I_{e_{1, 0}} \rightarrow \mathbb{Z}/(p^{r}-1)\mathbb{Z}, \ a_{e_{1, 0}} \mapsto (\sum_{e_{1}\in D_{X_{1}}\setminus \{e_{1, \infty}, e_{1, 0}\}}b^{\prime}_{e_{1}})-1,\end{align*} $$
and
Then the homomorphisms of inertia subgroups defined above induces a surjection
![]() $\delta _{1}: {\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{1}})^{\mathrm {ab}} \twoheadrightarrow \mathbb {Z}/(p^{r}-1)\mathbb {Z}.$
Note that
$\delta _{1}: {\pi }_{1}^{\mathrm {t}}(U_{X_{1}}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{1}})^{\mathrm {ab}} \twoheadrightarrow \mathbb {Z}/(p^{r}-1)\mathbb {Z}.$
Note that
![]() $\text {ker}(\delta _{1})$
does not depend on the choices of the generators
$\text {ker}(\delta _{1})$
does not depend on the choices of the generators
![]() $\{a_{e_{1}}\}_{e_{1} \in D_{X_{1}}}$
.
$\{a_{e_{1}}\}_{e_{1} \in D_{X_{1}}}$
.
Let
![]() $I_{\widetilde e_{2}} \stackrel {\mathrm {def}}{=} \phi (I_{\widetilde e_{1}})$
,
$I_{\widetilde e_{2}} \stackrel {\mathrm {def}}{=} \phi (I_{\widetilde e_{1}})$
,
![]() $\widetilde e_{1} \in D_{\widetilde X_{1}}$
, and
$\widetilde e_{1} \in D_{\widetilde X_{1}}$
, and
![]() $I_{e_{2}}$
,
$I_{e_{2}}$
,
![]() $e_{2} \in D_{X_{2}}$
, the image of the natural homomorphism
$e_{2} \in D_{X_{2}}$
, the image of the natural homomorphism
![]() $I_{\widetilde e_{2}} \hookrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})^{\mathrm {ab}}.$
Since
$I_{\widetilde e_{2}} \hookrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})^{\mathrm {ab}}.$
Since
![]() $(p, p^{r}-1)=1$
, by Theorem 3.14,
$(p, p^{r}-1)=1$
, by Theorem 3.14,
![]() $\delta _{1}$
and the isomorphism
$\delta _{1}$
and the isomorphism
![]() $\phi ^{p'}: {\pi }_{1}^{\mathrm {t}}(U_{X_{1}})^{p'} \stackrel {\sim }{\rightarrow } {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})^{p'}$
imply the following homomorphisms of inertia subgroups:
$\phi ^{p'}: {\pi }_{1}^{\mathrm {t}}(U_{X_{1}})^{p'} \stackrel {\sim }{\rightarrow } {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})^{p'}$
imply the following homomorphisms of inertia subgroups:
 $$ \begin{align*}\ I_{e_{2, 0}} \rightarrow \mathbb{Z}/(p^{r}-1)\mathbb{Z}, \ a_{e_{2, 0}} \mapsto (\sum_{e_{1}\in D_{X_{1}}\setminus \{e_{1, \infty}, e_{1, 0}\}}b^{\prime}_{e_{1}})-1,\end{align*} $$
$$ \begin{align*}\ I_{e_{2, 0}} \rightarrow \mathbb{Z}/(p^{r}-1)\mathbb{Z}, \ a_{e_{2, 0}} \mapsto (\sum_{e_{1}\in D_{X_{1}}\setminus \{e_{1, \infty}, e_{1, 0}\}}b^{\prime}_{e_{1}})-1,\end{align*} $$
and
where
![]() $a_{e_{2}}$
,
$a_{e_{2}}$
,
![]() $e_{2} \in D_{X_{2}}$
, denotes the element induced by
$e_{2} \in D_{X_{2}}$
, denotes the element induced by
![]() $a_{e_{1}}$
,
$a_{e_{1}}$
,
![]() $e_{1} \in D_{X_{1}}$
, via
$e_{1} \in D_{X_{1}}$
, via
![]() $\phi $
. Then the homomorphisms of inertia subgroups defined above induce a surjection
$\phi $
. Then the homomorphisms of inertia subgroups defined above induce a surjection
![]() $\delta _{2}: {\pi }_{1}^{\mathrm {t}}(U_{X_{2}}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})^{\mathrm {ab}} \twoheadrightarrow \mathbb {Z}/(p^{r}-1)\mathbb {Z}.$
$\delta _{2}: {\pi }_{1}^{\mathrm {t}}(U_{X_{2}}) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})^{\mathrm {ab}} \twoheadrightarrow \mathbb {Z}/(p^{r}-1)\mathbb {Z}.$
We put
![]() $H_{\delta _{i}}\stackrel {\mathrm {def}}{=} \text {ker}(\delta _{i}),\ M_{\delta _{i}} \stackrel {\mathrm {def}}{=} H^{\mathrm {ab}}_{\delta _{i}} \otimes \mathbb {F}_{p}, \ i \in \{1, 2\}.$
Note that we have
$H_{\delta _{i}}\stackrel {\mathrm {def}}{=} \text {ker}(\delta _{i}),\ M_{\delta _{i}} \stackrel {\mathrm {def}}{=} H^{\mathrm {ab}}_{\delta _{i}} \otimes \mathbb {F}_{p}, \ i \in \{1, 2\}.$
Note that we have
![]() $H_{\delta _{1}}=\phi ^{-1}(H_{\delta _{2}})$
. Write
$H_{\delta _{1}}=\phi ^{-1}(H_{\delta _{2}})$
. Write
![]() $(X_{H_{\delta _{i}}}, D_{X_{H_{\delta _{i}}}})$
for the smooth pointed stable curve over
$(X_{H_{\delta _{i}}}, D_{X_{H_{\delta _{i}}}})$
for the smooth pointed stable curve over
![]() $k_{i}$
induced by
$k_{i}$
induced by
![]() $H_{\delta _{i}}$
. The
$H_{\delta _{i}}$
. The
![]() $\mathbb {F}_{p}$
-vector space
$\mathbb {F}_{p}$
-vector space
![]() $M_{\delta _{i}}$
admits a natural action of
$M_{\delta _{i}}$
admits a natural action of
![]() $I_{\widetilde e_{i, \infty }}$
via conjugation which coincides with the action via the following character
$I_{\widetilde e_{i, \infty }}$
via conjugation which coincides with the action via the following character
We put
![]() $M_{\delta _{i}}[\chi _{I_{\widetilde e_{i, \infty }}, r}]\stackrel {\mathrm {def}}{=} \{a\in M_{\delta _{i}}\otimes _{\mathbb {F}_{p}} \mathbb {F}_{\widetilde e_{i, \infty }} \ |\ \sigma (a)=\chi _{I_{\widetilde e_{i, \infty }}, r}(\sigma )a \ \text {for all} \ \sigma \in I_{\widetilde e_{i, \infty }}\}$
, where
$M_{\delta _{i}}[\chi _{I_{\widetilde e_{i, \infty }}, r}]\stackrel {\mathrm {def}}{=} \{a\in M_{\delta _{i}}\otimes _{\mathbb {F}_{p}} \mathbb {F}_{\widetilde e_{i, \infty }} \ |\ \sigma (a)=\chi _{I_{\widetilde e_{i, \infty }}, r}(\sigma )a \ \text {for all} \ \sigma \in I_{\widetilde e_{i, \infty }}\}$
, where
![]() $\sigma (a)$
,
$\sigma (a)$
,
![]() $\sigma \in I_{\widetilde e_{i, \infty }}$
, is the induced action of the conjugacy action of
$\sigma \in I_{\widetilde e_{i, \infty }}$
, is the induced action of the conjugacy action of
![]() $I_{\widetilde e_{i, \infty }}$
on
$I_{\widetilde e_{i, \infty }}$
on
![]() $H_{\delta _{i}}$
. In fact,
$H_{\delta _{i}}$
. In fact,
![]() $\text {dim}_{\mathbb {F}_{\widetilde e_{i, \infty }}}(M_{\delta _{i}}[\chi _{I_{\widetilde e_{i, \infty }}, r}])$
is the first generalized Hasse-Witt invariant associated to the tame covering of
$\text {dim}_{\mathbb {F}_{\widetilde e_{i, \infty }}}(M_{\delta _{i}}[\chi _{I_{\widetilde e_{i, \infty }}, r}])$
is the first generalized Hasse-Witt invariant associated to the tame covering of
![]() $U_{X_{i}}$
corresponding to
$U_{X_{i}}$
corresponding to
![]() $H_{\delta _{i}} \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
(see [Reference YangY5, Section 2.2]). Since the action of
$H_{\delta _{i}} \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
(see [Reference YangY5, Section 2.2]). Since the action of
![]() $I_{\widetilde e_{i}, \infty }$
on
$I_{\widetilde e_{i}, \infty }$
on
![]() $M_{\delta _{i}}$
is semisimple, we obtain a surjection
$M_{\delta _{i}}$
is semisimple, we obtain a surjection
![]() $M_{\delta _{1}}[\chi _{I_{\widetilde e_{1, \infty }}, r}] \twoheadrightarrow M_{\delta _{2}}[\chi _{I_{\widetilde e_{2, \infty }}, r}]$
induced by
$M_{\delta _{1}}[\chi _{I_{\widetilde e_{1, \infty }}, r}] \twoheadrightarrow M_{\delta _{2}}[\chi _{I_{\widetilde e_{2, \infty }}, r}]$
induced by
![]() $\phi |_{H_{\delta _{1}}}$
and
$\phi |_{H_{\delta _{1}}}$
and
![]() $\theta _{\phi , \widetilde e_{1, \infty }, \widetilde e_{2, \infty }}$
. On the other hand, the third and the final paragraphs of the proof of [Reference TamagawaT2, Lemma 3.3] imply that the linear condition
$\theta _{\phi , \widetilde e_{1, \infty }, \widetilde e_{2, \infty }}$
. On the other hand, the third and the final paragraphs of the proof of [Reference TamagawaT2, Lemma 3.3] imply that the linear condition
 $$ \begin{align*}\sum_{e_{1}\in D_{X_{1}}\setminus \{e_{1, \infty}, e_{1, 0}\}}b_{e_{1}}e_{1}=e_{1, 0}\end{align*} $$
$$ \begin{align*}\sum_{e_{1}\in D_{X_{1}}\setminus \{e_{1, \infty}, e_{1, 0}\}}b_{e_{1}}e_{1}=e_{1, 0}\end{align*} $$
with respect to
![]() $e_{1, \infty }$
and
$e_{1, \infty }$
and
![]() $e_{1, 0}$
on
$e_{1, 0}$
on
![]() $(X_{1}, D_{X_{1}})$
holds if and only if
$(X_{1}, D_{X_{1}})$
holds if and only if
![]() $M_{\delta _{1}}[\chi _{I_{\widetilde e_{1, \infty }}, r}]=0$
. Thus, we obtain
$M_{\delta _{1}}[\chi _{I_{\widetilde e_{1, \infty }}, r}]=0$
. Thus, we obtain
![]() $M_{\delta _{2}}[\chi _{I_{\widetilde e_{2, \infty }}, r}] =0$
. Then the third and the final paragraphs of the proof of [Reference TamagawaT2, Lemma 3.3] imply that the linear condition
$M_{\delta _{2}}[\chi _{I_{\widetilde e_{2, \infty }}, r}] =0$
. Then the third and the final paragraphs of the proof of [Reference TamagawaT2, Lemma 3.3] imply that the linear condition
 $$ \begin{align*}\sum_{e_{1}\in D_{X_{1}}\setminus \{e_{1, \infty}, e_{1, 0}\}}b_{e_{1}}\rho_{\phi}(e_{1})=e_{2, 0}\end{align*} $$
$$ \begin{align*}\sum_{e_{1}\in D_{X_{1}}\setminus \{e_{1, \infty}, e_{1, 0}\}}b_{e_{1}}\rho_{\phi}(e_{1})=e_{2, 0}\end{align*} $$
with respect to
![]() $e_{2, \infty }$
and
$e_{2, \infty }$
and
![]() $e_{2, 0}$
on
$e_{2, 0}$
on
![]() $(X_{2}, D_{X_{2}})$
holds. This completes the proof of the lemma.
$(X_{2}, D_{X_{2}})$
holds. This completes the proof of the lemma.
Remark 4.2.1. Note that, if
![]() $X_{1}=\mathbb {P}_{k}^{1}$
, then the linear condition is as follows:
$X_{1}=\mathbb {P}_{k}^{1}$
, then the linear condition is as follows:
 $$ \begin{align*}\sum_{e_{1}\in D_{X_{1}}\setminus \{\infty, 0\}}b_{e_{1}}e_{1}=0\end{align*} $$
$$ \begin{align*}\sum_{e_{1}\in D_{X_{1}}\setminus \{\infty, 0\}}b_{e_{1}}e_{1}=0\end{align*} $$
with respect to
![]() $\infty $
and
$\infty $
and
![]() $0$
.
$0$
.
4.1.4.
Now, we prove the first main theorem of the present paper.
Theorem 4.3. We maintain the notation and settings introduced above. Then we have the following:
(i)
![]() $d_{(X_{i}, D_{X_{i}})}$
,
$d_{(X_{i}, D_{X_{i}})}$
,
![]() $i\in \{1, 2\}$
, can be mono-anabelian reconstructed from
$i\in \{1, 2\}$
, can be mono-anabelian reconstructed from
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
.
${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
.
(ii) Suppose
![]() $k_{1}^{\mathrm {m}} \cong \overline {\mathbb {F}}_{p, 1}$
. Then the set of open continuous homomorphisms
$k_{1}^{\mathrm {m}} \cong \overline {\mathbb {F}}_{p, 1}$
. Then the set of open continuous homomorphisms
is nonempty if and only if
![]() $U_{X^{\mathrm {m}}_1} \cong U_{X^{\mathrm {m}}_2}$
as schemes. In particular, if this is the case, we have
$U_{X^{\mathrm {m}}_1} \cong U_{X^{\mathrm {m}}_2}$
as schemes. In particular, if this is the case, we have
![]() $k_{2}^{\mathrm {m}} \cong \overline {\mathbb {F}}_{p, 2}$
and
$k_{2}^{\mathrm {m}} \cong \overline {\mathbb {F}}_{p, 2}$
and
Proof. Firstly, let us prove the (ii). The “if” part of (ii) is trivial. We treat the “only if” part of (ii). Suppose that
![]() $\mathrm {Hom}^{\mathrm {op}}_{\mathrm {pg}}({\pi }_{1}^{\mathrm {t}}(U_{X_{1}}), {\pi }_{1}^{\mathrm {t}}(U_{X_{2}}))$
is a nonempty set, and let
$\mathrm {Hom}^{\mathrm {op}}_{\mathrm {pg}}({\pi }_{1}^{\mathrm {t}}(U_{X_{1}}), {\pi }_{1}^{\mathrm {t}}(U_{X_{2}}))$
is a nonempty set, and let
![]() $\phi \in \mathrm {Hom}^{\mathrm {op}}_{\mathrm {pg}}({\pi }_{1}^{\mathrm {t}}(U_{X_{1}}), {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})).$
Then Lemma 4.1 implies that
$\phi \in \mathrm {Hom}^{\mathrm {op}}_{\mathrm {pg}}({\pi }_{1}^{\mathrm {t}}(U_{X_{1}}), {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})).$
Then Lemma 4.1 implies that
![]() $\phi $
is a surjection.
$\phi $
is a surjection.
We identify
![]() $D^{\mathrm {gp}}_{X_{i}}, i\in \{1, 2\}$
, with
$D^{\mathrm {gp}}_{X_{i}}, i\in \{1, 2\}$
, with
![]() $D_{X_{i}}$
via the bijection
$D_{X_{i}}$
via the bijection
![]() ${\vartheta }_{X_{i}}: D_{X_{i}}^{\mathrm {gp}} \stackrel {\sim }{\rightarrow } D_{X_{i}}$
. Since
${\vartheta }_{X_{i}}: D_{X_{i}}^{\mathrm {gp}} \stackrel {\sim }{\rightarrow } D_{X_{i}}$
. Since
![]() $\phi $
is a surjection, Lemma 3.10 implies that
$\phi $
is a surjection, Lemma 3.10 implies that
![]() $\phi $
induces a bijection
$\phi $
induces a bijection
![]() $\rho _{\phi }: D_{X_{1}} \stackrel {\sim }{\rightarrow } D_{X_{2}}.$
We put
$\rho _{\phi }: D_{X_{1}} \stackrel {\sim }{\rightarrow } D_{X_{2}}.$
We put
![]() $e_{2, 0}\stackrel {\mathrm {def}}{=} \rho _{\phi }(e_{1, 0})$
and
$e_{2, 0}\stackrel {\mathrm {def}}{=} \rho _{\phi }(e_{1, 0})$
and
![]() $e_{2, \infty }\stackrel {\mathrm {def}}{=} \rho _{\phi }(e_{1, \infty })$
. Let
$e_{2, \infty }\stackrel {\mathrm {def}}{=} \rho _{\phi }(e_{1, \infty })$
. Let
![]() $\widetilde e_{2, 0} \in D_{\widetilde X_{2}}$
be a point over
$\widetilde e_{2, 0} \in D_{\widetilde X_{2}}$
be a point over
![]() $e_{2, 0}$
. Theorem 3.14 implies that there exists a point
$e_{2, 0}$
. Theorem 3.14 implies that there exists a point
![]() $\widetilde e_{1, 0} \in D_{\widetilde X_{1}}$
over
$\widetilde e_{1, 0} \in D_{\widetilde X_{1}}$
over
![]() $e_{1, 0}$
, such that
$e_{1, 0}$
, such that
![]() $\phi (I_{\widetilde e_{1, 0}})=I_{\widetilde e_{2, 0}}$
. Then
$\phi (I_{\widetilde e_{1, 0}})=I_{\widetilde e_{2, 0}}$
. Then
![]() $\mathbb {F}_{\widetilde e_{i, 0}}\stackrel {\mathrm {def}}{=} (I_{\widetilde e_{i, 0}}\otimes _{\mathbb {Z}} (\mathbb {Q}/\mathbb {Z})_{i}^{p'}) \sqcup \{*_{\widetilde e_{i, 0}}\}, \ i\in \{1, 2\},$
admits a structure of field. Moreover, Proposition 3.15 implies that the field structure can be mono-anabelian reconstructed from
$\mathbb {F}_{\widetilde e_{i, 0}}\stackrel {\mathrm {def}}{=} (I_{\widetilde e_{i, 0}}\otimes _{\mathbb {Z}} (\mathbb {Q}/\mathbb {Z})_{i}^{p'}) \sqcup \{*_{\widetilde e_{i, 0}}\}, \ i\in \{1, 2\},$
admits a structure of field. Moreover, Proposition 3.15 implies that the field structure can be mono-anabelian reconstructed from
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
, and that
${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
, and that
![]() $\phi $
induces a field isomorphism
$\phi $
induces a field isomorphism
![]() $\theta _{\phi , \widetilde e_{1, 0}, \widetilde e_{2, 0}}: \mathbb {F}_{\widetilde e_{1, 0}} \stackrel {\sim }{\rightarrow } \mathbb {F}_{\widetilde e_{2, 0}}.$
$\theta _{\phi , \widetilde e_{1, 0}, \widetilde e_{2, 0}}: \mathbb {F}_{\widetilde e_{1, 0}} \stackrel {\sim }{\rightarrow } \mathbb {F}_{\widetilde e_{2, 0}}.$
Proposition 3.2 (i) implies that n can be mono-anabelian reconstructed from
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
,
${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
,
![]() $i \in \{1, 2\}$
. If
$i \in \{1, 2\}$
. If
![]() $n=3$
, (ii) is trivial, so we may assume
$n=3$
, (ii) is trivial, so we may assume
![]() $n\geq 4.$
Moreover, since
$n\geq 4.$
Moreover, since
![]() $k_{1}^{\mathrm {m}}\cong \overline {\mathbb {F}}_{p, 1}$
, without loss of generality, we may assume that
$k_{1}^{\mathrm {m}}\cong \overline {\mathbb {F}}_{p, 1}$
, without loss of generality, we may assume that
![]() $k_{1}=\overline {\mathbb {F}}_{p, 1}=\mathbb {F}_{\widetilde e_{1, 0}},$
that
$k_{1}=\overline {\mathbb {F}}_{p, 1}=\mathbb {F}_{\widetilde e_{1, 0}},$
that
![]() $X_{1}=\mathbb {P}^{1}_{\overline {\mathbb {F}}_{p, 1}}$
, and that
$X_{1}=\mathbb {P}^{1}_{\overline {\mathbb {F}}_{p, 1}}$
, and that
Here,
![]() $e_{1, 2}, \dots , e_{1, n-2} \in \overline {\mathbb {F}}_{p, 1}\setminus \{e_{1, 0}, e_{1, 1}\}$
are distinct from each other.
$e_{1, 2}, \dots , e_{1, n-2} \in \overline {\mathbb {F}}_{p, 1}\setminus \{e_{1, 0}, e_{1, 1}\}$
are distinct from each other.
Step 1: In this step, we will construct a linear condition on a certain tame covering of
![]() $(X_{1}, D_{X_{1}})$
.
$(X_{1}, D_{X_{1}})$
.
We see that there exists a natural number r prime to p, such that
![]() $\mathbb {F}_{p}(\zeta _{r})$
contains rth roots of
$\mathbb {F}_{p}(\zeta _{r})$
contains rth roots of
![]() $e_{1, 2}, \dots , e_{1, n-2}$
, where
$e_{1, 2}, \dots , e_{1, n-2}$
, where
![]() $\zeta _{r}$
denotes a fixed primitive rth root of unity in
$\zeta _{r}$
denotes a fixed primitive rth root of unity in
![]() $\overline {\mathbb {F}}_{p, 1}$
. Let
$\overline {\mathbb {F}}_{p, 1}$
. Let
![]() $s\stackrel {\mathrm {def}}{=} [\mathbb {F}_{p}(\zeta _{r}): \mathbb {F}_{p}]$
. For each
$s\stackrel {\mathrm {def}}{=} [\mathbb {F}_{p}(\zeta _{r}): \mathbb {F}_{p}]$
. For each
![]() $e_{1, u} \in \{e_{1, 2}, \dots , e_{1, n-2}\}$
, we fix an rth root
$e_{1, u} \in \{e_{1, 2}, \dots , e_{1, n-2}\}$
, we fix an rth root
![]() $e_{1, u}^{1/r}$
in
$e_{1, u}^{1/r}$
in
![]() $\overline {\mathbb {F}}_{p, 1}$
. Then we have
$\overline {\mathbb {F}}_{p, 1}$
. Then we have
 $$ \begin{align*}e_{1, u}^{1/r}=\sum_{v=0}^{s-1}b_{1, uv}\zeta_{r}^{v}, \ u \in \{2, \dots, n-2\},\end{align*} $$
$$ \begin{align*}e_{1, u}^{1/r}=\sum_{v=0}^{s-1}b_{1, uv}\zeta_{r}^{v}, \ u \in \{2, \dots, n-2\},\end{align*} $$
where
![]() $b_{1, uv} \in \mathbb {F}_{p}$
for each
$b_{1, uv} \in \mathbb {F}_{p}$
for each
![]() $u\in \{2, \dots , n-2\}$
and each
$u\in \{2, \dots , n-2\}$
and each
![]() $v\in \{0, \dots , s-1\}$
.
$v\in \{0, \dots , s-1\}$
.
Let
![]() $X_{1} \setminus \{e_{1, \infty }\} =\mathrm {Spec} \, \overline {\mathbb {F}}_{p, 1}[x_{1}]$
,
$X_{1} \setminus \{e_{1, \infty }\} =\mathrm {Spec} \, \overline {\mathbb {F}}_{p, 1}[x_{1}]$
,
![]() $f_{H_{1}}: (X_{H_{1}}, D_{X_{H_{1}}}) \rightarrow (X_{1}, D_{X_{1}})$
the Galois tame covering over
$f_{H_{1}}: (X_{H_{1}}, D_{X_{H_{1}}}) \rightarrow (X_{1}, D_{X_{1}})$
the Galois tame covering over
![]() $\overline {\mathbb {F}}_{p, 1}$
with Galois group
$\overline {\mathbb {F}}_{p, 1}$
with Galois group
![]() $\mathbb {Z}/r\mathbb {Z}$
determined by the equation
$\mathbb {Z}/r\mathbb {Z}$
determined by the equation
![]() $y_{1}^{r}=x_{1}$
, and
$y_{1}^{r}=x_{1}$
, and
![]() $H_{1}$
the open normal subgroup of
$H_{1}$
the open normal subgroup of
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})$
induced by the tame covering
${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})$
induced by the tame covering
![]() $f_{H_{1}}$
. Then
$f_{H_{1}}$
. Then
![]() $f_{H_{1}}$
is totally ramified over
$f_{H_{1}}$
is totally ramified over
![]() $\{e_{1, \infty }=\infty , e_{1, 0}=0\}$
and is étale over
$\{e_{1, \infty }=\infty , e_{1, 0}=0\}$
and is étale over
![]() $D_{X_{1}} \setminus \{\infty , 0\}$
. Note that
$D_{X_{1}} \setminus \{\infty , 0\}$
. Note that
![]() $X_{H_{1}}= \mathbb {P}_{\overline {\mathbb {F}}_{p, 1}}^{1}$
, and that the points of
$X_{H_{1}}= \mathbb {P}_{\overline {\mathbb {F}}_{p, 1}}^{1}$
, and that the points of
![]() $D_{X_{H_{1}}}$
over
$D_{X_{H_{1}}}$
over
![]() $\{e_{1, \infty }, e_{1, 0}\}$
are
$\{e_{1, \infty }, e_{1, 0}\}$
are
![]() $\{e_{H_{1}, \infty }\stackrel {\mathrm {def}}{=} \infty , e_{H_{1}, 0}\stackrel {\mathrm {def}}{=} 0\}$
. We put
$\{e_{H_{1}, \infty }\stackrel {\mathrm {def}}{=} \infty , e_{H_{1}, 0}\stackrel {\mathrm {def}}{=} 0\}$
. We put
Thus, we obtain a linear condition
 $$ \begin{align*}e_{H_{1}, u}=\sum_{v=0}^{s-1}b_{1, uv}e_{H_{1}, 1}^{v}\end{align*} $$
$$ \begin{align*}e_{H_{1}, u}=\sum_{v=0}^{s-1}b_{1, uv}e_{H_{1}, 1}^{v}\end{align*} $$
with respect to
![]() $e_{H_{1}, \infty }$
and
$e_{H_{1}, \infty }$
and
![]() $e_{H_{1}, 0}$
on
$e_{H_{1}, 0}$
on
![]() $(X_{H_{1}}, D_{X_{H_{1}}})$
for each
$(X_{H_{1}}, D_{X_{H_{1}}})$
for each
![]() $\ u \in \{2, \dots , n-2\}.$
$\ u \in \{2, \dots , n-2\}.$
Step 2: In this step, we will prove that the linear condition on a certain tame covering of
![]() $(X_{1}, D_{X_{1}})$
constructed in Step 1 induces a linear condition on a certain tame covering of
$(X_{1}, D_{X_{1}})$
constructed in Step 1 induces a linear condition on a certain tame covering of
![]() $(X_{2}, D_{X_{2}})$
via the surjection
$(X_{2}, D_{X_{2}})$
via the surjection
![]() $\phi $
.
$\phi $
.
Write
![]() $H_{2}$
for
$H_{2}$
for
![]() $\phi (H_{1})$
. Since
$\phi (H_{1})$
. Since
![]() $(r, p)=1$
, we have the following commutative diagram of profinite groups:
$(r, p)=1$
, we have the following commutative diagram of profinite groups:

We denote by
![]() $f_{H_{2}}: (X_{H_{2}}, D_{X_{H_{2}}}) \rightarrow (X_{2}, D_{X_{2}})$
the Galois tame covering over
$f_{H_{2}}: (X_{H_{2}}, D_{X_{H_{2}}}) \rightarrow (X_{2}, D_{X_{2}})$
the Galois tame covering over
![]() $\overline {\mathbb {F}}_{p, 2}$
with Galois group
$\overline {\mathbb {F}}_{p, 2}$
with Galois group
![]() $\mathbb {Z}/r\mathbb {Z}$
induced by
$\mathbb {Z}/r\mathbb {Z}$
induced by
![]() $H_{2}$
. Note that Lemma 3.12 implies that
$H_{2}$
. Note that Lemma 3.12 implies that
![]() $(X_{H_{1}}, D_{X_{H_{1}}})$
and
$(X_{H_{1}}, D_{X_{H_{1}}})$
and
![]() $(X_{H_{2}}, D_{X_{H_{2}}})$
are equal types. Moreover, Lemma 3.11 implies that the following commutative diagram can be mono-anabelian reconstructed from the commutative diagram of profinite groups above:
$(X_{H_{2}}, D_{X_{H_{2}}})$
are equal types. Moreover, Lemma 3.11 implies that the following commutative diagram can be mono-anabelian reconstructed from the commutative diagram of profinite groups above:

We put
and
Remark 3.11.1 implies that
![]() $f_{H_{2}}$
is totally ramified over
$f_{H_{2}}$
is totally ramified over
![]() $\{e_{2, \infty }, e_{2, 0}\}$
and is étale over
$\{e_{2, \infty }, e_{2, 0}\}$
and is étale over
![]() $X_{2} \setminus \{e_{2, \infty }, e_{2, 0}\}$
. Then we may assume that
$X_{2} \setminus \{e_{2, \infty }, e_{2, 0}\}$
. Then we may assume that
![]() $X_{2}=\mathbb {P}^{1}_{k_{2}}$
, and that
$X_{2}=\mathbb {P}^{1}_{k_{2}}$
, and that
![]() $e_{2, \infty }=\infty , e_{2, 0}=0, e_{2,1}=1$
. We regard
$e_{2, \infty }=\infty , e_{2, 0}=0, e_{2,1}=1$
. We regard
![]() $e_{2, u}$
,
$e_{2, u}$
,
![]() $u \in \{2, \dots , n-2\}$
, as an element of
$u \in \{2, \dots , n-2\}$
, as an element of
![]() $k_{2} \setminus \{e_{2, 0}, e_{2, 1}\}$
. Moreover, we have
$k_{2} \setminus \{e_{2, 0}, e_{2, 1}\}$
. Moreover, we have
![]() $e_{H_{2}, \infty }=\infty $
and
$e_{H_{2}, \infty }=\infty $
and
![]() $e_{H_{2}, 0}=0$
.
$e_{H_{2}, 0}=0$
.
We put
![]() $\xi _{r}\stackrel {\mathrm {def}}{=} \theta _{\phi , \widetilde e_{1, 0}, \widetilde e_{2, 0}}(\zeta _{r})$
which is an rth root of unity in
$\xi _{r}\stackrel {\mathrm {def}}{=} \theta _{\phi , \widetilde e_{1, 0}, \widetilde e_{2, 0}}(\zeta _{r})$
which is an rth root of unity in
![]() $\mathbb {F}_{\widetilde e_{2, 0}}$
. Since
$\mathbb {F}_{\widetilde e_{2, 0}}$
. Since
![]() $\zeta _{r}(e_{H_{1}, 1}^{v})=e_{H_{1}, 1}^{v+1}$
, we obtain
$\zeta _{r}(e_{H_{1}, 1}^{v})=e_{H_{1}, 1}^{v+1}$
, we obtain
![]() $\xi _{r}(e_{H_{2}, 1}^{v})=e_{H_{2}, 1}^{v+1}, \ v\in \{0, \dots , s-2\}.$
By applying Lemma 4.2 for
$\xi _{r}(e_{H_{2}, 1}^{v})=e_{H_{2}, 1}^{v+1}, \ v\in \{0, \dots , s-2\}.$
By applying Lemma 4.2 for
![]() $\phi |_{H_{1}}: H_{1} \twoheadrightarrow H_{2}$
, the following linear condition
$\phi |_{H_{1}}: H_{1} \twoheadrightarrow H_{2}$
, the following linear condition
 $$ \begin{align*}e_{H_{2}, u}=\sum_{v=0}^{s-1}b_{1, uv}\xi_{r}^{v}(e^{0}_{H_{2}, 1})\end{align*} $$
$$ \begin{align*}e_{H_{2}, u}=\sum_{v=0}^{s-1}b_{1, uv}\xi_{r}^{v}(e^{0}_{H_{2}, 1})\end{align*} $$
with respect to
![]() $e_{H_{2}, \infty }$
and
$e_{H_{2}, \infty }$
and
![]() $e_{H_{2}, 0}$
on
$e_{H_{2}, 0}$
on
![]() $(X_{H_{2}}, D_{X_{H_{2}}})$
holds for each
$(X_{H_{2}}, D_{X_{H_{2}}})$
holds for each
![]() $u\in \{2, \dots , n-2\}$
. Since
$u\in \{2, \dots , n-2\}$
. Since
![]() $(e_{H_{2}, u})^{r}=e_{2, u}$
,
$(e_{H_{2}, u})^{r}=e_{2, u}$
,
![]() $u\in \{2, \dots , n-2\}$
, we obtain
$u\in \{2, \dots , n-2\}$
, we obtain
 $$ \begin{align*}e_{2, u}=(\sum_{v=0}^{s-1}b_{1, uv}\xi_{r}^{v}(e^{0}_{H_{2}, 1}))^{r}.\end{align*} $$
$$ \begin{align*}e_{2, u}=(\sum_{v=0}^{s-1}b_{1, uv}\xi_{r}^{v}(e^{0}_{H_{2}, 1}))^{r}.\end{align*} $$
Moreover, if we put
![]() $e_{H_{2}, 1}^{0}=1$
, then we obtain that
$e_{H_{2}, 1}^{0}=1$
, then we obtain that
 $$ \begin{align*}e_{2, u}=(\sum_{v=0}^{s-1}b_{1, uv}\xi_{r}^{v})^{r}\end{align*} $$
$$ \begin{align*}e_{2, u}=(\sum_{v=0}^{s-1}b_{1, uv}\xi_{r}^{v})^{r}\end{align*} $$
for each
![]() $u\in \{2, \dots , n-2\}$
. Since
$u\in \{2, \dots , n-2\}$
. Since
![]() $\theta _{\phi , \widetilde e_{1, 0}, \widetilde e_{2, 0}}(\zeta _{r})=\xi _{r}$
, we have
$\theta _{\phi , \widetilde e_{1, 0}, \widetilde e_{2, 0}}(\zeta _{r})=\xi _{r}$
, we have
 $$ \begin{align*}&U_{X_{1}}=U_{X_{1}^{\mathrm{m}}}=\mathbb{P}^{1}_{\overline{\mathbb{F}}_{p, 1}} \setminus \{e_{1, \infty}=\infty, e_{1, 0}=0, e_{1, 1}=1, e_{1, 2}, \dots, e_{1, n-2}\}\\&\quad \stackrel{\sim}{\rightarrow} \mathbb{P}^{1}_{\mathbb{F}_{\widetilde e_{2, 0}}} \setminus \{e_{2, \infty}=\infty, e_{2, 0}=0, e_{2, 1}=1, \theta_{\phi, \widetilde e_{1, 0}, \widetilde e_{2, 0}}(e_{1, 2}), \dots, \theta_{\phi, \widetilde e_{1, 0}, \widetilde e_{2, 0}}(e_{1, n-2})\}\\&\quad \cong\mathbb{P}^{1}_{\overline{\mathbb{F}}_{p, 2}} \setminus \{e_{2, \infty}=\infty, e_{2, 0}=0, e_{2, 1}=1, e_{2, 2}, \dots, e_{2, n-2}\} \end{align*} $$
$$ \begin{align*}&U_{X_{1}}=U_{X_{1}^{\mathrm{m}}}=\mathbb{P}^{1}_{\overline{\mathbb{F}}_{p, 1}} \setminus \{e_{1, \infty}=\infty, e_{1, 0}=0, e_{1, 1}=1, e_{1, 2}, \dots, e_{1, n-2}\}\\&\quad \stackrel{\sim}{\rightarrow} \mathbb{P}^{1}_{\mathbb{F}_{\widetilde e_{2, 0}}} \setminus \{e_{2, \infty}=\infty, e_{2, 0}=0, e_{2, 1}=1, \theta_{\phi, \widetilde e_{1, 0}, \widetilde e_{2, 0}}(e_{1, 2}), \dots, \theta_{\phi, \widetilde e_{1, 0}, \widetilde e_{2, 0}}(e_{1, n-2})\}\\&\quad \cong\mathbb{P}^{1}_{\overline{\mathbb{F}}_{p, 2}} \setminus \{e_{2, \infty}=\infty, e_{2, 0}=0, e_{2, 1}=1, e_{2, 2}, \dots, e_{2, n-2}\} \end{align*} $$
and
This means
![]() $U_{X^{\mathrm { m}}_{1}} \cong U_{X^{\mathrm {m}}_{2}}$
as schemes. In particular, we have
$U_{X^{\mathrm { m}}_{1}} \cong U_{X^{\mathrm {m}}_{2}}$
as schemes. In particular, we have
![]() $k_{2}^{\mathrm {m}} \cong \overline {\mathbb {F}}_{p,2}$
.
$k_{2}^{\mathrm {m}} \cong \overline {\mathbb {F}}_{p,2}$
.
Finally, we prove that
![]() $\mathrm {Hom}^{\mathrm {op}}_{\mathrm {pg}}({\pi }_{1}^{\mathrm {t}}(U_{X_{1}}), {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})) = \mathrm {Isom}_{\mathrm {pg}}({\pi }_{1}^{\mathrm {t}}(U_{X_{1}}), {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})).$
The “
$\mathrm {Hom}^{\mathrm {op}}_{\mathrm {pg}}({\pi }_{1}^{\mathrm {t}}(U_{X_{1}}), {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})) = \mathrm {Isom}_{\mathrm {pg}}({\pi }_{1}^{\mathrm {t}}(U_{X_{1}}), {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})).$
The “
![]() $\supseteq $
” part is trivial. We only need to prove the “
$\supseteq $
” part is trivial. We only need to prove the “
![]() $\subseteq $
” part. We may assume
$\subseteq $
” part. We may assume
![]() $\mathrm {Hom}^{\mathrm {op}}_{\mathrm {pg}}({\pi }_{1}^{\mathrm {t}}(U_{X_{1}}), {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})) \neq \emptyset .$
Let
$\mathrm {Hom}^{\mathrm {op}}_{\mathrm {pg}}({\pi }_{1}^{\mathrm {t}}(U_{X_{1}}), {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})) \neq \emptyset .$
Let
![]() $\phi ' \in \mathrm {Hom}^{\mathrm {op}}_{\mathrm {pg}}({\pi }_{1}^{\mathrm {t}}(U_{X_{1}}), {\pi }_{1}^{\mathrm {t}}(U_{X_{2}}))$
. Then
$\phi ' \in \mathrm {Hom}^{\mathrm {op}}_{\mathrm {pg}}({\pi }_{1}^{\mathrm {t}}(U_{X_{1}}), {\pi }_{1}^{\mathrm {t}}(U_{X_{2}}))$
. Then
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})$
is isomorphic to
${\pi }_{1}^{\mathrm {t}}(U_{X_{1}})$
is isomorphic to
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
as abstract profinite groups. By Lemma 4.1,
${\pi }_{1}^{\mathrm {t}}(U_{X_{2}})$
as abstract profinite groups. By Lemma 4.1,
![]() $\phi '$
is a surjection. Then [Reference Fried and JardenFJ, Proposition 16.10.6] implies that
$\phi '$
is a surjection. Then [Reference Fried and JardenFJ, Proposition 16.10.6] implies that
![]() $\phi '$
is an isomorphism. Thus, we obtain
$\phi '$
is an isomorphism. Thus, we obtain
![]() $\phi ' \in \mathrm {Isom}_{\mathrm { pro\text {-}gps}}({\pi }_{1}^{\mathrm {t}}(U_{X_{1}}), {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})).$
This completes the proof of (ii).
$\phi ' \in \mathrm {Isom}_{\mathrm { pro\text {-}gps}}({\pi }_{1}^{\mathrm {t}}(U_{X_{1}}), {\pi }_{1}^{\mathrm {t}}(U_{X_{2}})).$
This completes the proof of (ii).
Next, let us prove (i). Without loss of generality, we only treat the case where
![]() $i=1$
. Moreover, let
$i=1$
. Moreover, let
![]() $(X, D_{X}) \stackrel {\mathrm {def}}{=} (X_{1}, D_{X_{1}})$
,
$(X, D_{X}) \stackrel {\mathrm {def}}{=} (X_{1}, D_{X_{1}})$
,
![]() $k\stackrel {\mathrm {def}}{=} k_{1}$
, and
$k\stackrel {\mathrm {def}}{=} k_{1}$
, and
![]() $\overline {\mathbb {F}}_{p} \stackrel {\mathrm {def}}{=} \overline {\mathbb {F}}_{\widetilde e_{0} }$
. Let
$\overline {\mathbb {F}}_{p} \stackrel {\mathrm {def}}{=} \overline {\mathbb {F}}_{\widetilde e_{0} }$
. Let
![]() $(r, Q)$
be a pair, such that the following conditions hold: (i)
$(r, Q)$
be a pair, such that the following conditions hold: (i)
![]() $(r, p)=1$
; (ii) Q is an open normal subgroup of
$(r, p)=1$
; (ii) Q is an open normal subgroup of
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
, such that
${\pi }_{1}^{\mathrm {t}}(U_{X})$
, such that
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})/Q \cong \mathbb {Z}/r\mathbb {Z}$
, and that the Galois tame covering
${\pi }_{1}^{\mathrm {t}}(U_{X})/Q \cong \mathbb {Z}/r\mathbb {Z}$
, and that the Galois tame covering
![]() $f_{Q}: (X_{Q}, D_{X_{Q}}) \rightarrow (X, D_{X})$
over k induced by Q is totally ramified over
$f_{Q}: (X_{Q}, D_{X_{Q}}) \rightarrow (X, D_{X})$
over k induced by Q is totally ramified over
![]() $\{e_{\infty }, e_{0}\}$
and is étale over
$\{e_{\infty }, e_{0}\}$
and is étale over
![]() $D_{X} \setminus \{e_{\infty }, e_{0}\}$
.
$D_{X} \setminus \{e_{\infty }, e_{0}\}$
.
By applying Theorem 3.14, we see immediately that the set of pairs defined above can be mono-anabelian reconstructed from
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
.
${\pi }_{1}^{\mathrm {t}}(U_{X})$
.
We fix a primitive rth root of unity
![]() $\zeta _{r}$
in
$\zeta _{r}$
in
![]() $\overline {\mathbb {F}}_{p}$
and put
$\overline {\mathbb {F}}_{p}$
and put
![]() $s_{r} \stackrel {\mathrm {def}}{=} [\mathbb {F}_{p}(\zeta _{r}): \mathbb {F}_{p}]$
. Moreover, we put
$s_{r} \stackrel {\mathrm {def}}{=} [\mathbb {F}_{p}(\zeta _{r}): \mathbb {F}_{p}]$
. Moreover, we put
and let
![]() $e_{Q, u} \in D_{X_{Q}}$
,
$e_{Q, u} \in D_{X_{Q}}$
,
![]() $u \in \{2, \dots , n\}$
, such that
$u \in \{2, \dots , n\}$
, such that
![]() $f_{Q}(e_{Q, u})=e_{u}$
. Denote by
$f_{Q}(e_{Q, u})=e_{u}$
. Denote by
 $$ \begin{align*}L_{Q, u}\stackrel{\mathrm{def}}{=} \{e_{Q, u}-\sum_{v=0}^{s_{r}-1}b_{uv}e_{Q, 1}^{v} \ | \ b_{uv}\in \mathbb{F}_{p}\} \cap \{0\}, \ u \in \{2, \dots, n-2\}.\end{align*} $$
$$ \begin{align*}L_{Q, u}\stackrel{\mathrm{def}}{=} \{e_{Q, u}-\sum_{v=0}^{s_{r}-1}b_{uv}e_{Q, 1}^{v} \ | \ b_{uv}\in \mathbb{F}_{p}\} \cap \{0\}, \ u \in \{2, \dots, n-2\}.\end{align*} $$
By applying similar arguments to the arguments given in the proof of (ii) above, we have that
![]() $d_{(X, D_{X})}=0$
if and only if there exists a pair
$d_{(X, D_{X})}=0$
if and only if there exists a pair
![]() $(r, Q)$
defined above, such that
$(r, Q)$
defined above, such that
![]() $L_{Q, u} \neq \emptyset $
for each
$L_{Q, u} \neq \emptyset $
for each
![]() $u \in \{2, \dots , n-2\}$
. Then the third and the final paragraphs of the proof of [Reference TamagawaT2, Lemma 3.3] imply that
$u \in \{2, \dots , n-2\}$
. Then the third and the final paragraphs of the proof of [Reference TamagawaT2, Lemma 3.3] imply that
![]() $L_{Q, u}$
,
$L_{Q, u}$
,
![]() $u \in \{2, \dots , n-2\}$
, can be mono-anabelian reconstructed from Q. Thus,
$u \in \{2, \dots , n-2\}$
, can be mono-anabelian reconstructed from Q. Thus,
![]() $d_{(X, D_{X})}$
can be mono-anabelian reconstructed from
$d_{(X, D_{X})}$
can be mono-anabelian reconstructed from
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X})$
. This completes the proof of the theorem.
${\pi }_{1}^{\mathrm {t}}(U_{X})$
. This completes the proof of the theorem.
Remark 4.3.1. Note that Theorem 4.3 also holds if we replace
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
,
${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})$
,
![]() $i \in \{1, 2\}$
, by its maximal prosolvable quotient
$i \in \{1, 2\}$
, by its maximal prosolvable quotient
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})^{\mathrm {sol}}$
. Then we obtain the following solvable version of Theorem 4.3 which is slightly stronger than the original theorem:
${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})^{\mathrm {sol}}$
. Then we obtain the following solvable version of Theorem 4.3 which is slightly stronger than the original theorem:
We maintain the notation introduced above. Then
![]() $d_{(X_{i}, D_{X_{i}})}$
,
$d_{(X_{i}, D_{X_{i}})}$
,
![]() $i\in \{1, 2\}$
, can be mono-anabelian reconstructed from
$i\in \{1, 2\}$
, can be mono-anabelian reconstructed from
![]() ${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})^{\mathrm {sol}}$
. Moreover, suppose that
${\pi }_{1}^{\mathrm {t}}(U_{X_{i}})^{\mathrm {sol}}$
. Moreover, suppose that
![]() $k_{1}^{\mathrm { m}} \cong \overline {\mathbb {F}}_{p, 1}$
. Then the set of open continuous homomorphisms
$k_{1}^{\mathrm { m}} \cong \overline {\mathbb {F}}_{p, 1}$
. Then the set of open continuous homomorphisms
is nonempty if and only if
![]() $U_{X^{\mathrm {m}}_1} \cong U_{X^{\mathrm {m}}_2}$
as schemes. In particular, if this is the case, we have
$U_{X^{\mathrm {m}}_1} \cong U_{X^{\mathrm {m}}_2}$
as schemes. In particular, if this is the case, we have
![]() $k_{2}^{\mathrm {m}} \cong \overline {\mathbb {F}}_{p, 2}$
and
$k_{2}^{\mathrm {m}} \cong \overline {\mathbb {F}}_{p, 2}$
and
4.2. The second main theorem
In this subsection, by using Theorem 4.3, we prove a result concerning pointed collection conjecture and the Weak Hom-version Conjecture (Theorem 4.4).
4.2.1. Settings
We maintain the notation introduced in Section 2.1.2.
4.2.2.
Let
![]() $q \in M_{0, n}^{\mathrm {ord}}$
be an arbitrary point,
$q \in M_{0, n}^{\mathrm {ord}}$
be an arbitrary point,
![]() $\overline {k(q)}$
an algebraic closure of
$\overline {k(q)}$
an algebraic closure of
![]() $k(q)$
, and
$k(q)$
, and
as
![]() $\overline {k(q)}$
-schemes. We shall say that q is a coordinated point if either
$\overline {k(q)}$
-schemes. We shall say that q is a coordinated point if either
![]() $q=q_{\mathrm {gen}}$
or the following conditions are satisfied:
$q=q_{\mathrm {gen}}$
or the following conditions are satisfied:
-
(i)
 $\text {dim}(V_{q})=\text {dim}(M_{0, n}^{\mathrm {ord}})-1$
.
$\text {dim}(V_{q})=\text {dim}(M_{0, n}^{\mathrm {ord}})-1$
. -
(ii) There exists
 $i \in \{4, \dots , n\}$
, such that
$i \in \{4, \dots , n\}$
, such that
 $a_{i} \in \overline {\mathbb {F}}_{p}$
.
$a_{i} \in \overline {\mathbb {F}}_{p}$
.
Let
![]() $\omega ^{\setminus i}_{n, 4}: M_{0, n}^{\mathrm {ord}} \rightarrow M_{0, 4}^{\mathrm {ord}}$
be the morphism induced by the morphism
$\omega ^{\setminus i}_{n, 4}: M_{0, n}^{\mathrm {ord}} \rightarrow M_{0, 4}^{\mathrm {ord}}$
be the morphism induced by the morphism
![]() $\mathcal {M}_{0, n}^{\mathrm {ord}} \rightarrow \mathcal {M}_{0, 4}^{\mathrm {ord}}$
obtained by forgetting the marked points except the first, the second, the third, and the ith marked points. If q is a coordinated point and
$\mathcal {M}_{0, n}^{\mathrm {ord}} \rightarrow \mathcal {M}_{0, 4}^{\mathrm {ord}}$
obtained by forgetting the marked points except the first, the second, the third, and the ith marked points. If q is a coordinated point and
![]() $q\neq q_{\mathrm {gen}}$
, then we have that
$q\neq q_{\mathrm {gen}}$
, then we have that
![]() $q"\stackrel {\mathrm {def}}{=} \omega ^{\setminus i}_{n, 4}(q)$
is a closed point of
$q"\stackrel {\mathrm {def}}{=} \omega ^{\setminus i}_{n, 4}(q)$
is a closed point of
![]() $M_{0, 4}^{\mathrm {ord}}$
, and that
$M_{0, 4}^{\mathrm {ord}}$
, and that
![]() $(\omega ^{\setminus i}_{n, 4})^{-1}(q")=V_{q}$
since
$(\omega ^{\setminus i}_{n, 4})^{-1}(q")=V_{q}$
since
![]() $(\omega ^{\setminus i}_{n, 4})^{-1}(q")$
is an irreducible closed subset of dimension
$(\omega ^{\setminus i}_{n, 4})^{-1}(q")$
is an irreducible closed subset of dimension
![]() $\text {dim}(M_{0, n}^{\mathrm {ord}})-1$
containing
$\text {dim}(M_{0, n}^{\mathrm {ord}})-1$
containing
![]() $V_{q}$
.
$V_{q}$
.
Let t be a closed point of
![]() $M_{0, n}^{\mathrm {ord}}$
. Then there exists a set of coordinated points
$M_{0, n}^{\mathrm {ord}}$
. Then there exists a set of coordinated points
![]() $P_{t}\stackrel {\mathrm {def}}{=} \{q_{t, 4}, \dots , q_{t, n}\}$
, such that
$P_{t}\stackrel {\mathrm {def}}{=} \{q_{t, 4}, \dots , q_{t, n}\}$
, such that
 $$ \begin{align*}\{t\}=\bigcap_{q_{t, j} \in P_{t}}V_{q_{t, j}}.\end{align*} $$
$$ \begin{align*}\{t\}=\bigcap_{q_{t, j} \in P_{t}}V_{q_{t, j}}.\end{align*} $$
4.2.3.
Now, we prove the second main result of the present paper.
Theorem 4.4.
(i) For each closed point
![]() $t \in M_{0, n}^{\mathrm {ord, cl}}$
, the set
$t \in M_{0, n}^{\mathrm {ord, cl}}$
, the set
![]() $\mathcal {C}_{t}$
associated to t is a pointed collection (Definition 2.4). Moreover, for each pointed collection
$\mathcal {C}_{t}$
associated to t is a pointed collection (Definition 2.4). Moreover, for each pointed collection
![]() $\mathcal {C} \in \mathscr {C}_{q_{\mathrm {gen}}}$
, there exists a closed point
$\mathcal {C} \in \mathscr {C}_{q_{\mathrm {gen}}}$
, there exists a closed point
![]() $s \in M_{0, n}^{\mathrm {ord, cl}}$
, such that
$s \in M_{0, n}^{\mathrm {ord, cl}}$
, such that
![]() $\mathcal {C}=\mathcal {C}_{s}$
.
$\mathcal {C}=\mathcal {C}_{s}$
.
(ii) Let
![]() $q \in M_{0, n}^{\mathrm {ord}}$
be an arbitrary point. Then the the natural map
$q \in M_{0, n}^{\mathrm {ord}}$
be an arbitrary point. Then the the natural map
![]() $\mathrm {colle}_{q}: \mathscr {V}_{q}^{\mathrm {cl}} \rightarrow \mathscr {C}_{q}, \ [t] \mapsto \mathcal {C}_{t},$
is an injection.
$\mathrm {colle}_{q}: \mathscr {V}_{q}^{\mathrm {cl}} \rightarrow \mathscr {C}_{q}, \ [t] \mapsto \mathcal {C}_{t},$
is an injection.
(iii) Let
![]() $q \in M_{0, n}^{\mathrm {ord}}$
be an arbitrary point. Suppose that there exists a set of coordinated points
$q \in M_{0, n}^{\mathrm {ord}}$
be an arbitrary point. Suppose that there exists a set of coordinated points
![]() $P_{q}$
, such that
$P_{q}$
, such that
 $$ \begin{align*}V_{q} = \bigcap_{u \in P_{q}} V_{u}.\end{align*} $$
$$ \begin{align*}V_{q} = \bigcap_{u \in P_{q}} V_{u}.\end{align*} $$
Then the pointed collection conjecture holds for q. In particular, the pointed collection conjecture holds for each closed point of
![]() $M_{0, n}^{\mathrm {ord}}$
.
$M_{0, n}^{\mathrm {ord}}$
.
(iv) Let
![]() $q_{i} \in M_{0, n}^{\mathrm {ord}}$
,
$q_{i} \in M_{0, n}^{\mathrm {ord}}$
,
![]() $i\in \{1, 2\}$
, be an arbitrary point. Suppose that there exists a set of coordinated points
$i\in \{1, 2\}$
, be an arbitrary point. Suppose that there exists a set of coordinated points
![]() $P_{q_{1}}$
, such that
$P_{q_{1}}$
, such that
 $$ \begin{align*}V_{q_1} = \bigcap_{u \in P_{q_{1}}} V_{u}.\end{align*} $$
$$ \begin{align*}V_{q_1} = \bigcap_{u \in P_{q_{1}}} V_{u}.\end{align*} $$
Then the Weak Hom-version Conjecture holds. In particular, the Weak Hom-version Conjecture holds when
![]() $q_{1}$
is a closed point.
$q_{1}$
is a closed point.
Proof. Let us prove (i). We put
![]() $F_{t}\stackrel {\mathrm {def}}{=} \{t' \in M_{0,n}^{\mathrm {ord, cl}} \ |\ t \sim _{fe} t'\}$
. Let
$F_{t}\stackrel {\mathrm {def}}{=} \{t' \in M_{0,n}^{\mathrm {ord, cl}} \ |\ t \sim _{fe} t'\}$
. Let
![]() $t"$
be an arbitrary point of
$t"$
be an arbitrary point of
![]() $\bigcap _{G \in \pi ^{\mathrm {t}}_{A}(t)}U_{G}$
. Then, for each
$\bigcap _{G \in \pi ^{\mathrm {t}}_{A}(t)}U_{G}$
. Then, for each
![]() $G \in \pi ^{\mathrm {t}}_{A}(t)$
,
$G \in \pi ^{\mathrm {t}}_{A}(t)$
,
![]() $\text {Hom}_{\mathrm {pg}}^{\mathrm {surj}}({\pi }_{1}^{\mathrm {t}}(t"), G)$
is nonempty, where
$\text {Hom}_{\mathrm {pg}}^{\mathrm {surj}}({\pi }_{1}^{\mathrm {t}}(t"), G)$
is nonempty, where
![]() $\text {Hom}_{\mathrm {pg}}^{\mathrm {surj}}(-, -)$
denotes the subset of
$\text {Hom}_{\mathrm {pg}}^{\mathrm {surj}}(-, -)$
denotes the subset of
![]() $\text {Hom}^{\mathrm {open}}_{\mathrm {pg}}(-, -)$
whose elements are surjections. Since
$\text {Hom}^{\mathrm {open}}_{\mathrm {pg}}(-, -)$
whose elements are surjections. Since
![]() ${\pi }_{1}^{\mathrm {t}}(t")$
is topologically finitely generated, we obtain that the set
${\pi }_{1}^{\mathrm {t}}(t")$
is topologically finitely generated, we obtain that the set
![]() $\text {Hom}_{\mathrm {pg}}^{\mathrm {surj}}({\pi }_{1}^{\mathrm {t}}(t"), G)$
is finite. Then the set of open continuous homomorphisms
$\text {Hom}_{\mathrm {pg}}^{\mathrm {surj}}({\pi }_{1}^{\mathrm {t}}(t"), G)$
is finite. Then the set of open continuous homomorphisms
 $$ \begin{align*}\varprojlim_{G \in \pi^{\mathrm{t}}_{A}(t)}\text{Hom}_{\mathrm{pg}}^{\mathrm{surj}}({\pi}_{1}^{\mathrm{t}}(t"), G)=\text{Hom}^{\mathrm{surj}}_{\mathrm{pg}}({\pi}_{1}^{\mathrm{t}}(t"), {\pi}_{1}^{\mathrm{ t}}(t))\end{align*} $$
$$ \begin{align*}\varprojlim_{G \in \pi^{\mathrm{t}}_{A}(t)}\text{Hom}_{\mathrm{pg}}^{\mathrm{surj}}({\pi}_{1}^{\mathrm{t}}(t"), G)=\text{Hom}^{\mathrm{surj}}_{\mathrm{pg}}({\pi}_{1}^{\mathrm{t}}(t"), {\pi}_{1}^{\mathrm{ t}}(t))\end{align*} $$
is nonempty. Thus, Theorem 4.3 implies
![]() $t" \in F_{t}$
. This means
$t" \in F_{t}$
. This means
 $$ \begin{align*}(\bigcap_{G \in \pi^{\mathrm{t}}_{A}(t)}U_{G}) \cap M_{g, n}^{\mathrm{ord, cl}}=F_{t}.\end{align*} $$
$$ \begin{align*}(\bigcap_{G \in \pi^{\mathrm{t}}_{A}(t)}U_{G}) \cap M_{g, n}^{\mathrm{ord, cl}}=F_{t}.\end{align*} $$
Since
![]() $U_{X_{t}}$
can be defined over a finite field,
$U_{X_{t}}$
can be defined over a finite field,
![]() $F_{t}$
is a finite set. Then
$F_{t}$
is a finite set. Then
![]() $\mathcal {C}_{t}$
is a pointed collection.
$\mathcal {C}_{t}$
is a pointed collection.
Let
![]() $\mathcal {C} \in \mathscr {C}_{q_{\mathrm {gen}}}$
be a pointed collection and s a closed point of
$\mathcal {C} \in \mathscr {C}_{q_{\mathrm {gen}}}$
be a pointed collection and s a closed point of
![]() $\bigcap _{G \in \mathcal {C}}U_{G}$
. By replacing t by s, and by applying similar arguments to the arguments given in the proof above, we obtain
$\bigcap _{G \in \mathcal {C}}U_{G}$
. By replacing t by s, and by applying similar arguments to the arguments given in the proof above, we obtain
![]() $\mathcal {C}=\mathcal {C}_{s}$
.
$\mathcal {C}=\mathcal {C}_{s}$
.
(ii) follows immediately from Theorem 4.3. Let us prove (iii). If
![]() $n=4$
, then
$n=4$
, then
![]() $M_{0, 4}^{\mathrm {ord}}$
is a one dimension scheme. For each
$M_{0, 4}^{\mathrm {ord}}$
is a one dimension scheme. For each
![]() $q\in M_{0,4}^{\mathrm {ord}}$
, the pointed collection conjecture follows immediately from Theorem 4.3. Then we may assume
$q\in M_{0,4}^{\mathrm {ord}}$
, the pointed collection conjecture follows immediately from Theorem 4.3. Then we may assume
![]() $n\geq 5.$
To verify (iii), (ii) implies that we only need to prove that
$n\geq 5.$
To verify (iii), (ii) implies that we only need to prove that
![]() $\text {colle}_{q}$
is a surjection.
$\text {colle}_{q}$
is a surjection.
Suppose that q is a closed point of
![]() $M_{0, n}^{\mathrm {ord}}$
. Let
$M_{0, n}^{\mathrm {ord}}$
. Let
![]() $\mathcal {C}\in \mathscr {C}_{q}$
be an arbitrary pointed collection contained in
$\mathcal {C}\in \mathscr {C}_{q}$
be an arbitrary pointed collection contained in
![]() $\mathscr {C}_{q}$
. By applying (i), there exists a closed point
$\mathscr {C}_{q}$
. By applying (i), there exists a closed point
![]() $s\in M_{0, n}^{\mathrm {ord, cl}}$
, such that the pointed collection
$s\in M_{0, n}^{\mathrm {ord, cl}}$
, such that the pointed collection
![]() $\mathcal {C}_{s}$
associated to s is equal to
$\mathcal {C}_{s}$
associated to s is equal to
![]() $\mathcal {C}$
. Since
$\mathcal {C}$
. Since
![]() $\mathcal {C}\in \mathscr {C}_{q}$
, there exists a surjection
$\mathcal {C}\in \mathscr {C}_{q}$
, there exists a surjection
![]() ${\pi }_{1}^{\mathrm {t}}(q) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(s)$
. Then Theorem 4.3 implies
${\pi }_{1}^{\mathrm {t}}(q) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(s)$
. Then Theorem 4.3 implies
![]() ${\pi }_{1}^{\mathrm {t}}(q) \stackrel {\sim }{\rightarrow } {\pi }_{1}^{\mathrm {t}}(s)$
. Thus, we have
${\pi }_{1}^{\mathrm {t}}(q) \stackrel {\sim }{\rightarrow } {\pi }_{1}^{\mathrm {t}}(s)$
. Thus, we have
![]() ${\pi }_{A}(q)=\mathcal {C}_{s}=\mathcal {C}$
(or, equivalently,
${\pi }_{A}(q)=\mathcal {C}_{s}=\mathcal {C}$
(or, equivalently,
![]() $\mathscr {C}_{q}=\{{\pi }_{A}^{\mathrm {t}}(q)\}$
). In particular,
$\mathscr {C}_{q}=\{{\pi }_{A}^{\mathrm {t}}(q)\}$
). In particular,
![]() $\text {colle}_{q}$
is a surjection if q is a closed point of
$\text {colle}_{q}$
is a surjection if q is a closed point of
![]() $M_{0, n}^{\mathrm {ord}}$
.
$M_{0, n}^{\mathrm {ord}}$
.
Suppose that q is a nonclosed point. This means
![]() $\text {dim}(V_{q})\geq 1.$
If
$\text {dim}(V_{q})\geq 1.$
If
![]() $q=q_{\mathrm {gen}}$
, (iii) follows from (i) and (ii). Let us treat the case where
$q=q_{\mathrm {gen}}$
, (iii) follows from (i) and (ii). Let us treat the case where
![]() $q\neq q_{\mathrm {gen}}$
. First, suppose that q is a coordinated point, and that
$q\neq q_{\mathrm {gen}}$
. First, suppose that q is a coordinated point, and that
Without loss of generality, we may assume
![]() $a_{n} \in \overline {\mathbb {F}}_{p}$
.
$a_{n} \in \overline {\mathbb {F}}_{p}$
.
For each pointed collection
![]() $\mathcal {C} \subseteq \mathscr {C}_{q}$
, by applying (i), there exists a closed point
$\mathcal {C} \subseteq \mathscr {C}_{q}$
, by applying (i), there exists a closed point
![]() $t_{1} \in M_{g, n}^{\mathrm {ord, cl}}$
, such that
$t_{1} \in M_{g, n}^{\mathrm {ord, cl}}$
, such that
![]() $\mathcal {C}_{t_{1}}=\mathcal {C}$
. Then we have an open continuous surjective homomorphism
$\mathcal {C}_{t_{1}}=\mathcal {C}$
. Then we have an open continuous surjective homomorphism
![]() ${\pi }_{1}^{\mathrm {t}}(q) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(t_{1}).$
Let
${\pi }_{1}^{\mathrm {t}}(q) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(t_{1}).$
Let
![]() $\omega ^{\setminus n}_{n, 4}: M_{0, n}^{\mathrm {ord}} \rightarrow M_{0, 4}^{\mathrm {ord}}$
be the morphism induced by the morphism
$\omega ^{\setminus n}_{n, 4}: M_{0, n}^{\mathrm {ord}} \rightarrow M_{0, 4}^{\mathrm {ord}}$
be the morphism induced by the morphism
![]() $\mathcal {M}_{0, n}^{\mathrm {ord}} \rightarrow \mathcal {M}_{0, 4}^{\mathrm {ord}}$
obtained by forgetting the marked points except the first, the second, the third, and the nth marked points. We put
$\mathcal {M}_{0, n}^{\mathrm {ord}} \rightarrow \mathcal {M}_{0, 4}^{\mathrm {ord}}$
obtained by forgetting the marked points except the first, the second, the third, and the nth marked points. We put
![]() $t_{1}"\stackrel {\mathrm {def}}{=} \omega ^{\setminus n}_{n, 4}(t_{1})$
and
$t_{1}"\stackrel {\mathrm {def}}{=} \omega ^{\setminus n}_{n, 4}(t_{1})$
and
![]() $q"\stackrel {\mathrm {def}}{=} \omega ^{\setminus n}_{n, 4}(q)$
. Note that
$q"\stackrel {\mathrm {def}}{=} \omega ^{\setminus n}_{n, 4}(q)$
. Note that
![]() $t_{1}"$
and
$t_{1}"$
and
![]() $q"$
are closed points of
$q"$
are closed points of
![]() $M_{0, 4}$
. Write
$M_{0, 4}$
. Write
![]() $(X_{q}, D_{X_{q}})$
,
$(X_{q}, D_{X_{q}})$
,
![]() $(X_{t_{1}}, D_{X_{t_{1}}})$
,
$(X_{t_{1}}, D_{X_{t_{1}}})$
,
![]() $(X_{q"}, D_{X_{q"}})$
, and
$(X_{q"}, D_{X_{q"}})$
, and
![]() $(X_{t_{1}"}, D_{X_{t_{1}"}})$
for the smooth pointed stable curves corresponding to q,
$(X_{t_{1}"}, D_{X_{t_{1}"}})$
for the smooth pointed stable curves corresponding to q,
![]() $t_{1}$
,
$t_{1}$
,
![]() $q"$
and
$q"$
and
![]() $t_{1}"$
, respectively.
$t_{1}"$
, respectively.
We denote by
![]() $I_{q} \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{q}})={\pi }_{1}^{\mathrm {t}}(q)$
the normal closed subgroup generated by
$I_{q} \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{q}})={\pi }_{1}^{\mathrm {t}}(q)$
the normal closed subgroup generated by
![]() $I_{\widetilde e} \in \text {Ine}({\pi }_{1}^{\mathrm {t}}(U_{X_{q}}))$
,
$I_{\widetilde e} \in \text {Ine}({\pi }_{1}^{\mathrm {t}}(U_{X_{q}}))$
,
![]() $e\in D_{X_{q}}\setminus D_{X_{q"}}$
, where
$e\in D_{X_{q}}\setminus D_{X_{q"}}$
, where
![]() $\widetilde e \in D_{\widetilde X_{q}}$
is an element over e (see Section 3.1.3 for
$\widetilde e \in D_{\widetilde X_{q}}$
is an element over e (see Section 3.1.3 for
![]() $D_{\widetilde X_{q}}$
), and
$D_{\widetilde X_{q}}$
), and
![]() $I_{t_{1}} \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{t_{1}}})={\pi }_{1}^{\mathrm { t}}(t_{1})$
the normal closed subgroup generated by
$I_{t_{1}} \subseteq {\pi }_{1}^{\mathrm {t}}(U_{X_{t_{1}}})={\pi }_{1}^{\mathrm { t}}(t_{1})$
the normal closed subgroup generated by
![]() $I_{\widetilde e} \in \text {Ine}({\pi }_{1}^{\mathrm {t}}(U_{X_{t_{1}}}))$
,
$I_{\widetilde e} \in \text {Ine}({\pi }_{1}^{\mathrm {t}}(U_{X_{t_{1}}}))$
,
![]() $e\in D_{X_{t_{1}}}\setminus D_{X_{t_{1}"}}$
. Note that we have
$e\in D_{X_{t_{1}}}\setminus D_{X_{t_{1}"}}$
. Note that we have
![]() ${\pi }_{1}^{\mathrm {t}}(q)/I_{q} \stackrel {\sim }{\rightarrow } {\pi }_{1}^{\mathrm {t}}(q")$
and
${\pi }_{1}^{\mathrm {t}}(q)/I_{q} \stackrel {\sim }{\rightarrow } {\pi }_{1}^{\mathrm {t}}(q")$
and
![]() ${\pi }_{1}^{\mathrm {t}}(t_{1})/I_{t_{1}} \stackrel {\sim }{\rightarrow } {\pi }_{1}^{\mathrm {t}}(t_{1}")$
. Moreover, Theorem 3.14 implies that the image of
${\pi }_{1}^{\mathrm {t}}(t_{1})/I_{t_{1}} \stackrel {\sim }{\rightarrow } {\pi }_{1}^{\mathrm {t}}(t_{1}")$
. Moreover, Theorem 3.14 implies that the image of
![]() $I_{q}$
under the surjection
$I_{q}$
under the surjection
![]() ${\pi }_{1}^{\mathrm {t}}(q) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(t_{1})$
is
${\pi }_{1}^{\mathrm {t}}(q) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(t_{1})$
is
![]() $I_{t_{1}}$
. Then the surjection
$I_{t_{1}}$
. Then the surjection
![]() ${\pi }_{1}^{\mathrm {t}}(q) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(t_{1})$
induces an open continuous surjective homomorphism
${\pi }_{1}^{\mathrm {t}}(q) \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(t_{1})$
induces an open continuous surjective homomorphism
![]() ${\pi }_{1}^{\mathrm {t}}(q") \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(t_{1}").$
Thus, by Theorem 4.3, we obtain that
${\pi }_{1}^{\mathrm {t}}(q") \twoheadrightarrow {\pi }_{1}^{\mathrm {t}}(t_{1}").$
Thus, by Theorem 4.3, we obtain that
![]() $q" \sim _{fe} t_{1}".$
Then without loss of generality, we may assume
$q" \sim _{fe} t_{1}".$
Then without loss of generality, we may assume
![]() $q"=t_{1}"$
and
$q"=t_{1}"$
and
over
![]() $\overline {\mathbb {F}}_{p}$
, where
$\overline {\mathbb {F}}_{p}$
, where
![]() $b_{i} \in \overline {\mathbb {F}}_{p}$
for each
$b_{i} \in \overline {\mathbb {F}}_{p}$
for each
![]() $i \in \{4, \dots , n-1\}$
. Furthermore, we see
$i \in \{4, \dots , n-1\}$
. Furthermore, we see
![]() $t_{1}\in (\omega ^{\setminus n}_{n, 4})^{-1}(t_{1}")=(\omega ^{\setminus n}_{n, 4})^{-1}(q")=V_{q}$
. Thus,
$t_{1}\in (\omega ^{\setminus n}_{n, 4})^{-1}(t_{1}")=(\omega ^{\setminus n}_{n, 4})^{-1}(q")=V_{q}$
. Thus,
![]() $t_{1}$
is a closed point of
$t_{1}$
is a closed point of
![]() $V_{q}$
. Then the pointed collection conjecture holds for q when q is a coordinated point.
$V_{q}$
. Then the pointed collection conjecture holds for q when q is a coordinated point.
Next, we prove the general case. If
![]() $V_{q} = \bigcap _{u \in P_{q}} V_{u}$
, then
$V_{q} = \bigcap _{u \in P_{q}} V_{u}$
, then
![]() $V_{q}^{\mathrm {cl}}=\bigcap _{u \in P_{q}} V_{u}^{\mathrm {cl}}$
and
$V_{q}^{\mathrm {cl}}=\bigcap _{u \in P_{q}} V_{u}^{\mathrm {cl}}$
and
![]() $\bigcap _{u \in P_{q}} \mathscr {C}_{u}=\mathscr {C}_{q}$
. Moreover, since we have a bijection
$\bigcap _{u \in P_{q}} \mathscr {C}_{u}=\mathscr {C}_{q}$
. Moreover, since we have a bijection
![]() $\text {colle}_{u}:\mathscr {V}_{u}^{\mathrm {cl}} \stackrel {\sim }{\rightarrow } \mathscr {C}_{u}$
for each
$\text {colle}_{u}:\mathscr {V}_{u}^{\mathrm {cl}} \stackrel {\sim }{\rightarrow } \mathscr {C}_{u}$
for each
![]() $u \in P_{q},$
we have that
$u \in P_{q},$
we have that
 $$ \begin{align*}\text{colle}_{q}: \mathscr{V}^{\mathrm{cl}}_{q}= \bigcap_{u \in P_{q}} \mathscr{V}^{\mathrm{cl}}_{u} \rightarrow \bigcap_{u \in P_{q}} \mathscr{C}_{u}=\mathscr{C}_{q}\end{align*} $$
$$ \begin{align*}\text{colle}_{q}: \mathscr{V}^{\mathrm{cl}}_{q}= \bigcap_{u \in P_{q}} \mathscr{V}^{\mathrm{cl}}_{u} \rightarrow \bigcap_{u \in P_{q}} \mathscr{C}_{u}=\mathscr{C}_{q}\end{align*} $$
is a bijection. This completes the proof of (iii).
Let us prove (iv). We only need to prove the “only if” part of the Weak Hom-version Conjecture. Suppose that
![]() $V_{q_2}$
is not essentially contained in
$V_{q_2}$
is not essentially contained in
![]() $V_{q_{1}}$
. This implies that there exists a closed point
$V_{q_{1}}$
. This implies that there exists a closed point
![]() $t_{2} \in V_{q_{2}}^{\mathrm {cl}}$
, such that
$t_{2} \in V_{q_{2}}^{\mathrm {cl}}$
, such that
![]() $F_{t_{2}} \cap V_{q_{1}}=\emptyset $
, where
$F_{t_{2}} \cap V_{q_{1}}=\emptyset $
, where
![]() $F_{t_{2}}\stackrel {\mathrm {def}}{=} \{t_{2}' \in M_{0,n}^{\mathrm {ord, cl}} \ |\ t_{2} \sim _{fe} t_{2}'\}$
. By (iii), we have
$F_{t_{2}}\stackrel {\mathrm {def}}{=} \{t_{2}' \in M_{0,n}^{\mathrm {ord, cl}} \ |\ t_{2} \sim _{fe} t_{2}'\}$
. By (iii), we have
![]() $\mathcal {C}_{t_{2}} \not \in \mathscr {C}_{q_{1}}$
. Thus, by Lemma 4.1, we obtain that
$\mathcal {C}_{t_{2}} \not \in \mathscr {C}_{q_{1}}$
. Thus, by Lemma 4.1, we obtain that
This provides a contradiction to the assumption that
![]() $\text {Hom}^{\mathrm {op}}_{\text {pg}}({\pi }_{1}^{\mathrm {t}}(q_{1}), {\pi }_{1}^{\mathrm {t}}(q_{2}))$
is nonempty. We complete the proof of (iv).
$\text {Hom}^{\mathrm {op}}_{\text {pg}}({\pi }_{1}^{\mathrm {t}}(q_{1}), {\pi }_{1}^{\mathrm {t}}(q_{2}))$
is nonempty. We complete the proof of (iv).
Remark 4.4.1. Let
![]() $q \in M_{g, n}$
be an arbitrary point. Stevenson posed a question as follows (see [Reference StevensonSte, Question 4.3] for the case of
$q \in M_{g, n}$
be an arbitrary point. Stevenson posed a question as follows (see [Reference StevensonSte, Question 4.3] for the case of
![]() $n=0$
): Does
$n=0$
): Does
![]() $\bigcap _{G \in {\pi }_{A}^{\mathrm {t}}(q)} U_{G}$
contain any closed points of
$\bigcap _{G \in {\pi }_{A}^{\mathrm {t}}(q)} U_{G}$
contain any closed points of
![]() $M_{g, n}$
? By [Reference TamagawaT5, Theorem 0.3],
$M_{g, n}$
? By [Reference TamagawaT5, Theorem 0.3],
![]() $\bigcap _{G \in {\pi }_{A}^{\mathrm {t}}(q)} U_{G}$
contains a closed point of
$\bigcap _{G \in {\pi }_{A}^{\mathrm {t}}(q)} U_{G}$
contains a closed point of
![]() $M_{g, n}$
if and only if q is a closed point of
$M_{g, n}$
if and only if q is a closed point of
![]() $M_{g, n}$
. Furthermore, when
$M_{g, n}$
. Furthermore, when
![]() $g=0$
and q is a closed point, the proof of Theorem 4.4 (i) implies that
$g=0$
and q is a closed point, the proof of Theorem 4.4 (i) implies that
 $$ \begin{align*}(\bigcap_{G \in {\pi}_{A}^{\mathrm{t}}(q)} U_{G})\cap M_{0, n}^{\mathrm{cl}}=F_{q},\end{align*} $$
$$ \begin{align*}(\bigcap_{G \in {\pi}_{A}^{\mathrm{t}}(q)} U_{G})\cap M_{0, n}^{\mathrm{cl}}=F_{q},\end{align*} $$
where
![]() $F_{q}\stackrel {\mathrm {def}}{=} \{q' \in M_{0,n}^{\mathrm {cl}} \ |\ q \sim _{fe} q'\}$
.
$F_{q}\stackrel {\mathrm {def}}{=} \{q' \in M_{0,n}^{\mathrm {cl}} \ |\ q \sim _{fe} q'\}$
.
Acknowledgments
The main philosophy of the present paper was conceived in a general discussion about understanding the mystery of fundamental groups in positive characteristic during a stroll through Manshuin Temple (located northeast of central Kyoto) in the summer of 2017.
The authors would like to thank the referee very much for understanding our research, for carefully reading the manuscript, and for giving us comments which substantially helped to improve the quality of the paper. The first author wishes to express gratitude to Professor Shinichi Mochizuki and the Research Institute for Mathematical Sciences (RIMS) for their hospitality and support during the author’s stay in Kyoto. The second author would like to thank Professor Akio Tamagawa for helpful comments. The second author was supported by the Research Institute for Mathematical Sciences (RIMS), an international joint usage/research center located in Kyoto University. The first and the third authors were supported by the National Natural Science Foundation of China Grant Number 12271253. The second author was supported by Japan Society for the Promotion of Science (JSPS) Grant-in-Aid for Young Scientists Grant Numbers 16J08847 and 20K14283.
Competing interest
The authors have no competing interest to declare.