Hostname: page-component-7479d7b7d-c9gpj Total loading time: 0 Render date: 2024-07-09T06:27:49.417Z Has data issue: false hasContentIssue false
  • English
  • Français

SPARSE APPROXIMATION AND RECOVERY BY GREEDY ALGORITHMS IN BANACH SPACES

Part of: Approximations and expansions Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  27 May 2014

V. N. TEMLYAKOV
V. N. TEMLYAKOV*
Affiliation:
University of South Carolina, USA Steklov Institute of Mathematics, Russia; temlyakovusc@gmail.com

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study sparse approximation by greedy algorithms. We prove the Lebesgue-type inequalities for the weak Chebyshev greedy algorithm (WCGA), a generalization of the weak orthogonal matching pursuit to the case of a Banach space. The main novelty of these results is a Banach space setting instead of a Hilbert space setting. The results are proved for redundant dictionaries satisfying certain conditions. Then we apply these general results to the case of bases. In particular, we prove that the WCGA provides almost optimal sparse approximation for the trigonometric system in 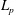$L_p$, 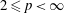$2\le p<\infty $.

MSC classification

Secondary: 41A65: Abstract approximation theory (approximation in normed linear spaces and other abstract spaces) 41A46: Approximation by arbitrary nonlinear expressions; widths and entropy 46B20: Geometry and structure of normed linear spaces
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 2 , 01 July 2014 , e12
Creative Commons
Creative Common License - CCCreative Common License - BY
The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution licence .
Copyright
© The Author 2014

References

Dai, W. and Milenkovic, O., ‘Subspace pursuit for compressive sensing signal reconstruction’, IEEE Trans. Inform. Theory 55 (2009), 2230–2249.CrossRefGoogle Scholar
Donoho, D., Elad, M. and Temlyakov, V. N., ‘On the Lebesgue type inequalities for greedy approximation’, J. Approx. Theory 147 (2007), 185–195.Google Scholar
Dilworth, S.J., Kalton, N.J. and Kutzarova, D., ‘On the existence of almost greedy bases in Banach spaces’, Studia Math. 158 (2003), 67–101.Google Scholar
Dilworth, S. J., Kalton, N. J., Kutzarova, D. and Temlyakov, V. N., ‘The thresholding greedy algorithm, greedy bases, and duality’, Constr. Approx. 19 (2003), 575–597.Google Scholar
Dilworth, S. J., Soto-Bajo, M. and Temlyakov, V. N., ‘Quasi-greedy bases and Lebesgue-type inequalities’, Sud. Math. 211 (2012), 41–69.Google Scholar
Gilbert, A. C., Muthukrishnan, S. and Strauss, M. J., ‘Approximation of functions over redundant dictionaries using coherence’, The 14th Annual ACM-SIAM Symposium on Discrete Algorithms (2003).Google Scholar
Foucart, S., ‘Sparse recovery algorithms: sufficient conditions in terms of restricted isometry constants’, in: Approximation Theory XIII: San Antonio, 2010 (2012), 65–77.Google Scholar
Konyagin, S. V. and Temlyakov, V. N., ‘A remark on greedy approximation in Banach spaces’, East. J. Approx. 5 (1999), 365–379.Google Scholar
Livshitz, E. D., ‘On the optimality of the Orthogonal Greedy Algorithm for $\mu $ -coherent dictionaries’, J. Approx. Theory 164 (5) (2012), 668–681.Google Scholar
Livshitz, E. D. and Temlyakov, V. N., ‘Sparse approximation and recovery by greedy algorithms’, arXiv:1303.3595v1 [math.NA] 14 Mar 2013.Google Scholar
Needell, D. and Tropp, J. A., ‘CoSaMP: iterative signal recovery from incomplete and inaccurate samples’, Appl. Comput. Harmonic Anal. 26 (2009), 301–321.Google Scholar
Needell, D. and Vershynin, R., ‘Uniform uncertainty principle and signal recovery via orthogonal matching pursuit’, Found. Comput. Math. 9 (2009), 317–334.Google Scholar
Nielsen, M., ‘An example of an almost greedy uniformly bounded orthonormal basis for $L_p(0,1)$ ’, J. Approx. Theory 149 (2007), 188–192.Google Scholar
Savu, D. and Temlyakov, V. N., ‘Lebesgue-type inequalities for greedy approximation in Banach spaces’, IEEE Trans. Inform. Theory 58 (2013), 1098–1106.Google Scholar
Temlyakov, V. N., ‘Greedy algorithm and $m$ -term trigonometric approximation’, Constr. Approx. 14 (1998), 569–587.Google Scholar
Temlyakov, V. N., ‘Greedy algorithms in Banach spaces’, Adv. Comput. Math. 14 (2001), 277–292.CrossRefGoogle Scholar
Temlyakov, V. N., ‘Nonlinear methods of approximation’, Found. Comput. Math. 3 (2003), 33–107.CrossRefGoogle Scholar
Temlyakov, V. N., Greedy Approximation, (Cambridge University Press, 2011).Google Scholar
Temlyakov, V. N., Yang, M. and Ye, P., ‘Greedy approximation with regard to non-greedy bases’, Adv. Comput. Math. 34 (2011), 319–337.CrossRefGoogle Scholar
Temlyakov, V. and Zheltov, P., ‘On performance of greedy algorithms’, J. Approx. Theory 163 (2011), 1134–1145.Google Scholar
Tropp, J. A., ‘Greed is good: Algorithmic results for sparse approximation’, IEEE Trans. Inform. Theory 50 (2004), 2231–2242.Google Scholar
Wang, J. and Shim, B., ‘Improved recovery bounds of orthogonal matching pursuit using restricted isometry property’, arXiv:1211.4293v1 [cs.IT] 19 Nov 2012.Google Scholar
Wojtaszczyk, P., ‘Greedy algorithm for general biorthogonal systems’, J. Approx. Theory 107 (2000), 293–314.CrossRefGoogle Scholar
Zhang, T., ‘Sparse recovery with orthogonal matching pursuit under RIP’, IEEE Trans. Inform. Theory 57 (2011), 6215–6221.Google Scholar