Hostname: page-component-848d4c4894-nmvwc Total loading time: 0 Render date: 2024-06-20T19:10:00.221Z Has data issue: false hasContentIssue false
  • English
  • Français

ROTH’S THEOREM FOR FOUR VARIABLES AND ADDITIVE STRUCTURES IN SUMS OF SPARSE SETS

Part of: Sequences and sets Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  19 February 2016

TOMASZ SCHOEN  and
OLOF SISASK
TOMASZ SCHOEN
Affiliation:
Faculty of Mathematics and Computer Science, Adam Mickiewicz University, Umultowska 87, 61-614 Poznań, Poland; schoen@amu.edu.pl
OLOF SISASK
Affiliation:
Department of Mathematics, KTH, 100 44 Stockholm, Sweden; sisask@kth.se

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that if 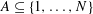$A\subset \{1,\ldots ,N\}$ does not contain any nontrivial solutions to the equation 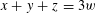$x+y+z=3w$, then

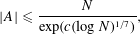$$\begin{eqnarray}|A|\leqslant \frac{N}{\exp (c(\log N)^{1/7})},\end{eqnarray}$$
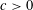where $c>0$ is some absolute constant. In view of Behrend’s construction, this bound is of the right shape: the exponent 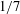$1/7$ cannot be replaced by any constant larger than 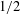$1/2$. We also establish a related result, which says that sumsets 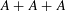$A+A+A$ contain long arithmetic progressions if 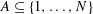$A\subset \{1,\ldots ,N\}$, or high-dimensional affine subspaces if 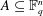$A\subset \mathbb{F}_{q}^{n}$, even if 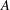$A$ has density of the shape above.

MSC classification

Primary: 11B30: Arithmetic combinatorics; higher degree uniformity
Secondary: 11B25: Arithmetic progressions 11K70: Harmonic analysis and almost periodicity
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 4 , 2016 , e5
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike licence (http://creativecommons.org/licenses/by-nc-sa/4.0/), which permits non-commercial re-use, distribution, and reproduction in any medium, provided the same Creative Commons licence is included and the original work is properly cited. The written permission of Cambridge University Press must be obtained for commercial re-use.
Copyright
©The Author(s) 2016

References

Bateman, M. and Katz, N. H., ‘New bounds on cap sets’, J. Amer. Math. Soc. 25(2) (2012), 585–613. arXiv:1101.5851.CrossRefGoogle Scholar
Behrend, F. A., ‘On sets of integers which contain no three terms in arithmetical progression’, Proc. Natl. Acad. Sci. USA 32 (1946), 331–332.CrossRefGoogle ScholarPubMed
Bloom, T. F., ‘Translation invariant equations and the method of Sanders’, Bull. Lond. Math. Soc. 44(5) (2012), 1050–1067. arXiv:1107.1110.CrossRefGoogle Scholar
Bloom, T. F., A quantitative improvement for Roth’s theorem on arithmetic progressions,arXiv:1405.5800.Google Scholar
Bourgain, J., ‘On triples in arithmetic progression’, Geom. Funct. Anal. 9(5) (1999), 968–984.CrossRefGoogle Scholar
Bourgain, J., ‘Roth’s theorem on progressions revisited’, J. Anal. Math. 104 (2008), 155–192.CrossRefGoogle Scholar
Croot, E., Łaba, I. and Sisask, O., ‘Arithmetic progressions in sumsets and L p -almost-periodicity’, Combin. Probab. Comput. 22(3) (2013), 351–365. arXiv:1103.6000.CrossRefGoogle Scholar
Croot, E., Ruzsa, I. Z. and Schoen, T., ‘Arithmetic progressions in sparse sumsets’, inCombinatorial Number Theory (de Gruyter, Berlin, 2007), 157–164.Google Scholar
Croot, E. and Sisask, O., ‘A new proof of Roth’s theorem on arithmetic progressions’, Proc. Amer. Math. Soc. 137 (2009), 805–809. arXiv:0801.2577.CrossRefGoogle Scholar
Croot, E. and Sisask, O., ‘A probabilistic technique for finding almost-periods of convolutions’, Geom. Funct. Anal. 20(6) (2010), 1367–1396. arXiv:1003.2978.CrossRefGoogle Scholar
Croot, E. and Sisask, O., Notes on proving Roth’s theorem using Bogolyubov’s method, http://people.math.gatech.edu/∼ecroot/bogolyubov-roth2.pdf.Google Scholar
Elkin, M., ‘An improved construction of progression-free sets’, Israel J. Math. 184 (2011), 93–128. arXiv:0801.4310.CrossRefGoogle Scholar
Freiman, G. A., Halberstam, H. and Ruzsa, I. Z., ‘Integer sum sets containing long arithmetic progressions’, J. Lond. Math. Soc. 46(2) (1992), 193–201.CrossRefGoogle Scholar
Green, B., ‘Arithmetic progressions in sumsets’, Geom. Funct. Anal. 12(3) (2002), 584–597.CrossRefGoogle Scholar
Green, B., ‘Finite field models in additive combinatorics’, inSurveys in Combinatorics 2005, London Mathematical Society Lecture Note Series, 327 (Cambridge University Press, Cambridge, 2005), 1–27. arXiv:math/0409420.Google Scholar
Green, B. and Ruzsa, I. Z., ‘Freiman’s theorem in an arbitrary abelian group’, J. Lond. Math. Soc. (2) 75(1) (2007), 163–175. arXiv:math/0505198.CrossRefGoogle Scholar
Green, B. and Wolf, J., ‘A note on Elkin’s improvement of Behrend’s construction’, inAdditive Number Theory (Springer, New York, 2010), 141–144. arXiv:0810.0732.CrossRefGoogle Scholar
Heath-Brown, D. R., ‘Integer sets containing no arithmetic progressions’, J. Lond. Math. Soc. (2) 35(3) (1987), 385–394.CrossRefGoogle Scholar
Henriot, K., ‘On arithmetic progressions in A + B + C ’, Int. Math. Res. Notices 2014(18) (2014), 5134–5164. arXiv:1211.4917.CrossRefGoogle Scholar
Roth, K. F., ‘On certain sets of integers’, J. Lond. Math. Soc. 28 (1953), 104–109.CrossRefGoogle Scholar
Sanders, T., ‘Additive structures in sumsets’, Math. Proc. Cambridge Philos. Soc. 144(2) (2008), 289–316. arXiv:math/0605520.CrossRefGoogle Scholar
Sanders, T., ‘Green’s sumset problem at density one half’, Acta Arith. 146(1) (2011), 91–101. arXiv:1003.5649.CrossRefGoogle Scholar
Sanders, T., ‘On Roth’s theorem on progressions’, Ann. of Math. (2) 174(1) (2011), 619–636. arXiv:1011.0104.CrossRefGoogle Scholar
Sanders, T., ‘On certain other sets of integers’, J. Anal. Math. 116 (2012), 53–82. arXiv:1007.5444.CrossRefGoogle Scholar
Sanders, T., ‘On the Bogolyubov-Ruzsa lemma’, Anal. PDE 5(3) (2012), 627–655. arXiv:1011.0107.CrossRefGoogle Scholar
Schoen, T. and Shkredov, I., ‘Roth’s theorem in many variables’, Israel J. Math. 199(1) (2014), 287–308. arXiv:1106.1601.CrossRefGoogle Scholar
Szemerédi, E., ‘Integer sets containing no arithmetic progressions’, Acta Math. Hungar. 56(1–2) (1990), 155–158.CrossRefGoogle Scholar
Tao, T. and Vu, V. H., Additive Combinatorics (Cambridge University Press, Cambridge, 2006).CrossRefGoogle Scholar