Hostname: page-component-7479d7b7d-k7p5g Total loading time: 0 Render date: 2024-07-09T06:28:08.900Z Has data issue: false hasContentIssue false
  • English
  • Français

Raising the level for 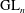$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\text {GL}_{{n}}$

Part of: Discontinuous groups and automorphic forms Lie groups

Published online by Cambridge University Press:  10 June 2014

JACK A. THORNE
JACK A. THORNE*
Affiliation:
Department of Mathematics, Harvard University, 1 Oxford Street, Cambridge, MA 02138, USA; thorne@math.harvard.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove a simple level-raising result for regular algebraic, conjugate self-dual automorphic forms on 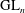$\mathrm{GL}_n$. This gives a systematic way to construct irreducible Galois representations whose residual representation is reducible.

MSC classification

Secondary: 11F33: Congruences for modular and $p$-adic modular forms 22E50: Representations of Lie and linear algebraic groups over local fields
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 2 , 01 July 2014 , e16
Creative Commons
Creative Common License - CCCreative Common License - BY
The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution licence .
Copyright
© The Author 2014

References

Bellaïche, J. and Graftieaux, P., ‘Augmentation du niveau pour U(3)’, Amer. J. Math. 128 (2) (2006), 271–309.CrossRefGoogle Scholar
Barnet-Lamb, T., Gee, T., Geraghty, D. and Taylor, R., ‘Potential automorphy and change of weight’, Ann. of Math. 179 (2) (2014), 501–609.CrossRefGoogle Scholar
Borel, A. and Wallach, N., Continuous cohomology, discrete subgroups, and representations of reductive groups, second edition, Mathematical Surveys and Monographs, 67 (American Mathematical Society, Providence, RI, 2000).CrossRefGoogle Scholar
Caraiani, A., ‘Local–global compatibility and the action of monodromy on nearby cycles’, Duke Math. J. 161 (12) (2012), 2311–2413.Google Scholar
Clozel, L., Harris, M. and Taylor, R., ‘Automorphy for some l-adic lifts of automorphic mod l Galois representations’, Publ. Math. Inst. Hautes Études Sci. (108) (2008), 1–181. With Appendix A, summarizing unpublished work of Russ Mann, and Appendix B by Marie-France Vignéras.Google Scholar
Clozel, L. and Thorne, J. A., ‘Level-raising and symmetric power functoriality, I’, Compos. Math. 150 (05) , 729–748.Google Scholar
Clozel, L. and Thorne, J. A., ‘Level-raising and symmetric power functoriality, II’, Ann. of Math. (to appear).Google Scholar
Gee, T., ‘Automorphic lifts of prescribed types’, Math. Ann. 350 (1) (2011), 107–144.Google Scholar
Geraghty, D., ‘Modularity lifting theorems for ordinary Galois representations’, Preprint.Google Scholar
Gross, B. H., ‘Algebraic modular forms’, Israel J. Math. 113 (1999), 61–93.CrossRefGoogle Scholar
Gross, B. H., ‘Some remarks on signs in functional equations’, Ramanujan J. 7 (1–3) (2003), 91–93. Rankin memorial issues.CrossRefGoogle Scholar
Guerberoff, L., ‘Modularity lifting theorems for Galois representations of unitary type’, Compos. Math. 147 (2011), 1022–1058.CrossRefGoogle Scholar
Harris, M., ‘The Taylor–Wiles method for coherent cohomology’, J. Reine Angew. Math. 679 (2013), 125–153.Google Scholar
Henniart, G., ‘Une caractérisation de la correspondance de Langlands locale pour GL(n)’, Bull. Soc. Math. France 130 (4) (2002), 587–602.Google Scholar
Harris, M. and Taylor, R., The geometry and cohomology of some simple shimura varieties, Annals of Mathematics Studies, 151 (Princeton University Press, Princeton, NJ, 2001), With an appendix by Vladimir G. Berkovich.Google Scholar
Ito, T., ‘Weight-monodromy conjecture for p-adically uniformized varieties’, Invent. Math. 159 (3) (2005), 607–656.Google Scholar
Labesse, J.-P., ‘Changement de base CM et séries discrètes’, in:Stab Trace Formula Shimura Var Arith Appl. vol. 1 (Int Press, Somerville, MA, 2011), 429–470.Google Scholar
Mok, C. P., ‘Endoscopic classification of representations of quasi-split unitary groups’, Memoirs of the AMS (to appear).Google Scholar
Lazarus, X., ‘Module universel non ramifié pour un groupe réductif $p$ -adique’, PhD thesis, L’Université Paris XI Orsay, March 2000.Google Scholar
Lan, K.-W. and Suh, J., ‘Vanishing theorems for torsion automorphic sheaves on compact PEL-type shimura varieties’, Duke Math. J. 161 (6) (2012), 1113–1170.Google Scholar
Mustafin, G. A., ‘Non-Archimedean uniformization’, Mat. Sb. (N.S.) 105 (147, 2) (1978), 207–237, 287.Google Scholar
Orlik, S., ‘On extensions of generalized steinberg representations’, J. Algebra 293 (2) (2005), 611–630.CrossRefGoogle Scholar
Ribet, K. A., ‘Congruence relations between modular forms’, in:Proceedings of the International Congress of Mathematicians, vol. 1, 2 (Warsaw, 1983) (PWN, Warsaw, 1984), 503–514.Google Scholar
Rapoport, M. and Zink, Th., Period spaces for p-divisible groups, Annals of Mathematics Studies, 141 (Princeton University Press, Princeton, NJ, 1996).Google Scholar
Saito, Takeshi, ‘Weight spectral sequences and independence of l ’, J. Inst. Math. Jussieu 2 (4) (2003), 583–634.Google Scholar
Shin, S. W., ‘Supercuspidal part of the mod $l$ cohomology of $\mathrm{GU}(1,n-1)$ -Shimura varieties’, J. Reine Angew Math. (to appear).Google Scholar
Tate, J., ‘Number theoretic background’, in:Automorphic forms, representations andL-functions, Proc. Sympos. Pure Math. (Oregon State University, Corvallis, OR, 1977), Part 2, Proc. Sympos. Pure Math. XXXIII (Amer. Math. Soc., Providence, RI, 1979), 3–26.Google Scholar
Taylor, R., ‘Automorphy for some l-adic lifts of automorphic mod l Galois representations II’, Publ. Math. Inst. Hautes Études Sci. 108 (2008), 183–239.CrossRefGoogle Scholar
Thorne, J. A., ‘Automorphy lifting theorems for residually reducible $l$ -adic Galois representations’, J. AMS, Preprint.Google Scholar
Taylor, R. and Yoshida, T., ‘Compatibility of local and global Langlands correspondences’, J. Amer. Math. Soc. 20 (2) (2007), 467–493.Google Scholar
Vignéras, M.-F., ‘Banal characteristic for reductive p-adic groups’, J. Number Theory 47 (3) (1994), 378–397.Google Scholar
Zelevinsky, A. V., ‘Induced representations of reductive p-adic groups II on irreducible representations of GL(n)’, Ann. Sci. École Norm. Sup. (4) 13 (2) (1980), 165–210.Google Scholar