Hostname: page-component-848d4c4894-xm8r8 Total loading time: 0 Render date: 2024-06-23T15:42:26.079Z Has data issue: false hasContentIssue false
  • English
  • Français

POINTWISE CONVERGENCE OF SCHRÖDINGER SOLUTIONS AND MULTILINEAR REFINED STRICHARTZ ESTIMATES

Part of: Harmonic analysis in several variables

Published online by Cambridge University Press:  13 August 2018

XIUMIN DU ,
LARRY GUTH ,
XIAOCHUN LI  and
RUIXIANG ZHANG
XIUMIN DU
Affiliation:
Institute for Advanced Study, Princeton, NJ, USA; xdu@math.ias.edu
LARRY GUTH
Affiliation:
Massachusetts Institute of Technology, Cambridge, MA, USA; lguth@math.mit.edu
XIAOCHUN LI
Affiliation:
University of Illinois at Urbana-Champaign, Urbana, IL, USA; xcli@math.uiuc.edu
RUIXIANG ZHANG
Affiliation:
Institute for Advanced Study, Princeton, NJ; rzhang@math.ias.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

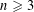We obtain partial improvement toward the pointwise convergence problem of Schrödinger solutions, in the general setting of fractal measure. In particular, we show that, for $n\geqslant 3$, 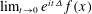$\lim _{t\rightarrow 0}e^{it\unicode[STIX]{x1D6E5}}f(x)$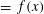$=f(x)$ almost everywhere with respect to Lebesgue measure for all 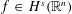$f\in H^{s}(\mathbb{R}^{n})$ provided that 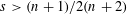$s>(n+1)/2(n+2)$. The proof uses linear refined Strichartz estimates. We also prove a multilinear refined Strichartz using decoupling and multilinear Kakeya.

MSC classification

Primary: 42B37: Harmonic analysis and PDE
Secondary: 42B15: Multipliers
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 6 , 2018 , e14
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives licence (http://creativecommons.org/licenses/by-nc-nd/4.0/), which permits non-commercial re-use, distribution, and reproduction in any medium, provided the original work is unaltered and is properly cited. The written permission of Cambridge University Press must be obtained for commercial re-use or in order to create a derivative work.
Copyright
© The Author(s) 2018

References

Barceló, J. A., Bennett, J., Carbery, A. and Rogers, K. M., ‘On the dimension of divergence sets of dispersive equations’, Math. Ann. 349 (2011), 599–622.Google Scholar
Bennett, J., Carbery, A. and Tao, T., ‘On the multilinear restriction and Kakeya conjectures’, Acta Math. 196 (2006), 261–302.Google Scholar
Bourgain, J., ‘On the Schrödinger maximal function in higher dimension’, Proc. Steklov Inst. Math. 2013 280, 46–60.Google Scholar
Bourgain, J., ‘A note on the Schrödinger maximal function’, J. Anal. Math. 130 (2016), 393–396.Google Scholar
Bourgain, J. and Demeter, C., ‘The proof of the l 2 decoupling conjecture’, Ann. of Math. (2) 182(1) (2015), 351–389.Google Scholar
Carleson, L., ‘Some analytic problems related to statistical mechanics’, inEuclidean Harmonic Analysis (Proc. Sem., Univ. Maryland, College Park, MD, 1979), Lecture Notes in Mathematics, 779 (Springer, Berlin, 1980), 5–45.Google Scholar
Dahlberg, B. E. J. and Kenig, C. E., ‘A note on the almost everywhere behavior of solutions to the Schrödinger equation’, inHarmonic Analysis (Minneapolis, MN, 1981), Lecture Notes in Mathematics, 908 (Springer, Berlin–New York, 1982), 205–209.Google Scholar
Du, X., Guth, L. and Li, X., ‘A sharp Schrödinger maximal estimate in ℝ2 ’, Ann. of Math. (2) 186 (2017), 607–640.Google Scholar
Du, X., Guth, L., Ou, Y., Wang, H., Wilson, B. and Zhang, R., ‘Weighted restriction estimates and application to Falconer distance set problem’, Preprint, 2018, arXiv:1802.10186.Google Scholar
Guth, L., ‘A short proof of the multilinear Kakeya inequality’, Math. Proc. Cambridge Philos. Soc. 158(1) (2015), 147–153.Google Scholar
Guth, L., ‘A restriction estimate using polynomial partitioning’, J. Amer. Math. Soc. 29(2) (2016), 371–413.Google Scholar
Guth, L., ‘Restriction estimates using polynomial partitioning II’, Preprint, 2016, arXiv:1603.04250.Google Scholar
Lee, S., ‘On pointwise convergence of the solutions to Schrödinger equations in ℝ2 ’, Int. Math. Res. Not. IMRN 2006 32597 (2006), 1–21.Google Scholar
Lucà, R. and Rogers, K., ‘Average decay for the Fourier transform of measures with applications’, J. Eur. Math. Soc. (2016), (to appear).Google Scholar
Lucà, R. and Rogers, K., ‘Coherence on fractals versus convergence for the Schrödinger equation’, Comm. Math. Phys. 351 (2017), 341–359.Google Scholar
Lucà, R. and Rogers, K., ‘A note on pointwise convergence for the Schrödinger equation’, Preprint, 2017, arXiv:1703.01360.Google Scholar
Sjögren, P. and Sjölin, P., ‘Convergence properties for the time-dependent Schrödinger equation’, Ann. Acad. Sci. Fenn. 14(1) (1989), 13–25.Google Scholar
Žubrinić, D., ‘Singular sets of Sobolev functions’, C. R. Math. Acad. Sci. Paris 334 (2002), 539–544.Google Scholar