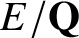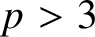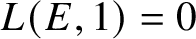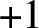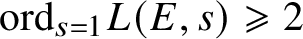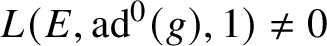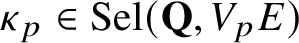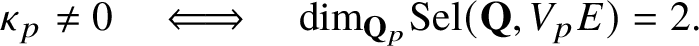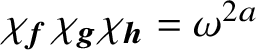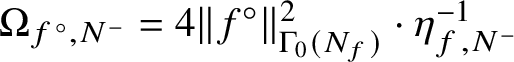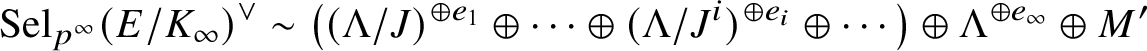1 Introduction
Let E be an elliptic curve over
![]() $\mathbf {Q}$
(hence modular [Reference Wiles51, Reference Taylor and Wiles46, Reference Breuil, Conrad, Diamond and Taylor8]) with associated L-function
$\mathbf {Q}$
(hence modular [Reference Wiles51, Reference Taylor and Wiles46, Reference Breuil, Conrad, Diamond and Taylor8]) with associated L-function
![]() $L(E,s)$
. In the late 1980s, a major advance towards the Birch and Swinnerton-Dyer (BSD) conjecture was the proof, by Gross–Zagier and Kolyvagin, of the implication
$L(E,s)$
. In the late 1980s, a major advance towards the Birch and Swinnerton-Dyer (BSD) conjecture was the proof, by Gross–Zagier and Kolyvagin, of the implication
In the proof of
![]() $(1.1)$
an imaginary quadratic field
$(1.1)$
an imaginary quadratic field
![]() $K/\mathbf {Q}$
is chosen such that
$K/\mathbf {Q}$
is chosen such that
![]() $\text {ord}_{s=1}L(E/K,s)=1$
and for which a Heegner point
$\text {ord}_{s=1}L(E/K,s)=1$
and for which a Heegner point
![]() $y_{K}\in E(\mathbf {Q})$
can be constructed using the theory of complex multiplication and a modular parametrisation of E. By the Gross–Zagier formula [Reference Gross and Zagier21], the nonvanishing of
$y_{K}\in E(\mathbf {Q})$
can be constructed using the theory of complex multiplication and a modular parametrisation of E. By the Gross–Zagier formula [Reference Gross and Zagier21], the nonvanishing of
![]() $L^{\prime }(E/K,1)$
implies that
$L^{\prime }(E/K,1)$
implies that
![]() $y_{K}$
has infinite order and the proof of (1.1) is reduced to the proof of the implication
$y_{K}$
has infinite order and the proof of (1.1) is reduced to the proof of the implication
which is a celebrated theorem by Kolyvagin [Reference Kolyvagin31].
A more recent major advance towards BSD arises from the works of Kato [Reference Kato29], Skinner–Urban [Reference Skinner and Urban45] and Xin Wan [Reference Wan49] on the Iwasawa main conjectures for elliptic modular forms, which, in particular, yield a proof of a p-converse to (1.2)
for certain primes p of good ordinary reduction for E, an implication first realised by Skinner [Reference Skinner43]. (A different proof of (1.3) was obtained independently by Wei Zhang [Reference Zhang53] as a consequence of his proof of Kolyvagin’s conjecture.) Together with the Gross–Zagier formula, (1.3) yields a p-converse to the theorem
![]() $(1.1)$
of Gross–Zagier and Kolyvagin.
$(1.1)$
of Gross–Zagier and Kolyvagin.
It is natural to ask about the extension of these results to elliptic curves
![]() $E/\mathbf {Q}$
of rank
$E/\mathbf {Q}$
of rank
![]() $r>1$
. As a first step in this direction, in this article we prove certain analogues of (1.2) and (1.3) in rank 2, with
$r>1$
. As a first step in this direction, in this article we prove certain analogues of (1.2) and (1.3) in rank 2, with
![]() $y_{K}$
replaced by a generalised Kato class
$y_{K}$
replaced by a generalised Kato class
introduced by Darmon–Rotger. Here,
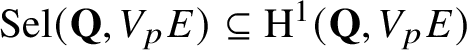 $\text {Sel}(\mathbf {Q},V_{p}E)\subseteq \text {H}^{1}(\mathbf {Q},V_{p}E)$
is the p-adic Selmer group fitting into the exact sequence
$\text {Sel}(\mathbf {Q},V_{p}E)\subseteq \text {H}^{1}(\mathbf {Q},V_{p}E)$
is the p-adic Selmer group fitting into the exact sequence
where
is the p-adic Tate module of the Tate–Shafarevich group
.
1.1 The Darmon–Rotger conjecture
We begin by briefly recalling the construction of
![]() $\kappa _{p}$
by Darmon–Rotger [Reference Darmon and Rotger18, Reference Darmon and Rotger17]. One starts by associating a global cohomology class
$\kappa _{p}$
by Darmon–Rotger [Reference Darmon and Rotger18, Reference Darmon and Rotger17]. One starts by associating a global cohomology class
 $$ \begin{align*} \kappa_{\gamma,\delta}(f,g,h)\in\textrm{H}^{1}(\mathbf{Q},V_{fgh}),\nonumber \end{align*} $$
$$ \begin{align*} \kappa_{\gamma,\delta}(f,g,h)\in\textrm{H}^{1}(\mathbf{Q},V_{fgh}),\nonumber \end{align*} $$
where
![]() $V_{fgh}=V_{p}(f)\otimes V_{p}(g)\otimes V_{p}(h)$
is the tensor product of the p-adic Galois representations associated to f, g and h to the data of
$V_{fgh}=V_{p}(f)\otimes V_{p}(g)\otimes V_{p}(h)$
is the tensor product of the p-adic Galois representations associated to f, g and h to the data of
-
• a triple of eigenforms
 $(f,g,h)\in S_{2}(\Gamma _{0}(N_{f}))\times S_{1}(\Gamma _{0}(N_{g}),\chi )\times S_{1}(\Gamma _{0}(N_{h}),\bar {\chi })$
of weights
$(f,g,h)\in S_{2}(\Gamma _{0}(N_{f}))\times S_{1}(\Gamma _{0}(N_{g}),\chi )\times S_{1}(\Gamma _{0}(N_{h}),\bar {\chi })$
of weights
 $(2,1,1)$
and levels prime-to-p with (1.4)
$(2,1,1)$
and levels prime-to-p with (1.4) $$ \begin{align} \textrm{gcd}(N_{f},N_{g}N_{h})=1, \end{align} $$
$$ \begin{align} \textrm{gcd}(N_{f},N_{g}N_{h})=1, \end{align} $$
-
• a choice of roots
 $\gamma \in \{\alpha _{g},\beta _{g}\}$
and
$\gamma \in \{\alpha _{g},\beta _{g}\}$
and
 $\delta \in \{\alpha _{h},\beta _{h}\}$
of the Hecke polynomials of g and h at p, assumed to be regular; that is,
$\delta \in \{\alpha _{h},\beta _{h}\}$
of the Hecke polynomials of g and h at p, assumed to be regular; that is,
 $\alpha _{g}\neq \beta _{g}$
and
$\alpha _{g}\neq \beta _{g}$
and
 $\alpha _{h}\neq \beta _{h}$
.
$\alpha _{h}\neq \beta _{h}$
.
Letting
![]() $g^{\flat }$
and
$g^{\flat }$
and
![]() $h^{\flat }$
be the p-stabilisations of g and h with
$h^{\flat }$
be the p-stabilisations of g and h with
![]() $U_{p}$
-eigenvalue
$U_{p}$
-eigenvalue
![]() $\gamma $
and
$\gamma $
and
![]() $\delta $
, the class
$\delta $
, the class
![]() $\kappa _{\gamma ,\delta }(f,g,h)$
is defined as the p-adic limit
$\kappa _{\gamma ,\delta }(f,g,h)$
is defined as the p-adic limit
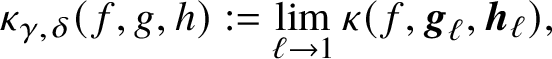 $$ \begin{align} \kappa_{\gamma,\delta}(f,g,h):=\lim_{\ell\to 1}\kappa(f,{\boldsymbol{g}}_{\ell},{\boldsymbol{h}}_{\ell}), \end{align} $$
$$ \begin{align} \kappa_{\gamma,\delta}(f,g,h):=\lim_{\ell\to 1}\kappa(f,{\boldsymbol{g}}_{\ell},{\boldsymbol{h}}_{\ell}), \end{align} $$
where
![]() $({\boldsymbol {g}}_{\ell },{\boldsymbol {h}}_{\ell })$
runs over the classical weight
$({\boldsymbol {g}}_{\ell },{\boldsymbol {h}}_{\ell })$
runs over the classical weight
![]() $\ell \geqslant 2$
specialisations of Hida families
$\ell \geqslant 2$
specialisations of Hida families
![]() ${\boldsymbol {g}}$
and
${\boldsymbol {g}}$
and
![]() ${\boldsymbol {h}}$
passing through
${\boldsymbol {h}}$
passing through
![]() $g^{\flat }$
and
$g^{\flat }$
and
![]() $h^{\flat }$
in weight
$h^{\flat }$
in weight
![]() $1$
, and
$1$
, and
![]() $\kappa (f,{\boldsymbol {h}}_{\ell },{\boldsymbol {h}}_{\ell })$
is obtained from the p-adic étale Abel–Jacobi image of generalised Gross–Kudla–Schoen diagonal cycles [Reference Gross and Kudla20, Reference Gross and Schoen22].
$\kappa (f,{\boldsymbol {h}}_{\ell },{\boldsymbol {h}}_{\ell })$
is obtained from the p-adic étale Abel–Jacobi image of generalised Gross–Kudla–Schoen diagonal cycles [Reference Gross and Kudla20, Reference Gross and Schoen22].
Remark 1.1. Under assumption (1.4), the sign in the functional equation for the triple product L-series
![]() $L(s,f\otimes {\boldsymbol {g}}_{\ell }\otimes {\boldsymbol {h}}_{\ell })$
is
$L(s,f\otimes {\boldsymbol {g}}_{\ell }\otimes {\boldsymbol {h}}_{\ell })$
is
![]() $-1$
for all
$-1$
for all
![]() $\ell \geqslant 2$
; in particular,
$\ell \geqslant 2$
; in particular,
![]() $L(1,f\otimes {\boldsymbol {g}}_{\ell }\otimes {\boldsymbol {h}}_{\ell })=0$
, and by the Gross–Zagier formula for diagonal cycles (proved in [Reference Yuan, Zhang and Zhang52] for
$L(1,f\otimes {\boldsymbol {g}}_{\ell }\otimes {\boldsymbol {h}}_{\ell })=0$
, and by the Gross–Zagier formula for diagonal cycles (proved in [Reference Yuan, Zhang and Zhang52] for
![]() $\ell =2$
) the classes
$\ell =2$
) the classes
![]() $\kappa (f,{\boldsymbol {g}}_{\ell },{\boldsymbol {h}}_{\ell })$
should be nontrivial precisely when
$\kappa (f,{\boldsymbol {g}}_{\ell },{\boldsymbol {h}}_{\ell })$
should be nontrivial precisely when
![]() $L^{\prime }(1,f\otimes {\boldsymbol {g}}_{\ell }\otimes {\boldsymbol {h}}_{\ell })\neq 0$
. On the other hand, the global root number of
$L^{\prime }(1,f\otimes {\boldsymbol {g}}_{\ell }\otimes {\boldsymbol {h}}_{\ell })\neq 0$
. On the other hand, the global root number of
![]() $L(s,f\otimes g\otimes h)$
is
$L(s,f\otimes g\otimes h)$
is
![]() $+1$
and it is precisely this sign change phenomenon between weights
$+1$
and it is precisely this sign change phenomenon between weights
![]() $\ell \geqslant 2$
and
$\ell \geqslant 2$
and
![]() $\ell =1$
that makes it possible for the p-adic limit construction (1.5) to yield interesting cohomology classes in situations of even analytic rank; in fact, as we recall below, classes that are crystalline at p precisely when
$\ell =1$
that makes it possible for the p-adic limit construction (1.5) to yield interesting cohomology classes in situations of even analytic rank; in fact, as we recall below, classes that are crystalline at p precisely when
![]() $\text {ord}_{s=1}L(s,f\otimes g\otimes h)\geqslant 2$
.
$\text {ord}_{s=1}L(s,f\otimes g\otimes h)\geqslant 2$
.
Under the hypothesis that
![]() $p>3$
is a prime of good ordinary reduction for f, the explicit reciprocity law of [Reference Darmon and Rotger18] yields a formula of the form
$p>3$
is a prime of good ordinary reduction for f, the explicit reciprocity law of [Reference Darmon and Rotger18] yields a formula of the form
where
 $\text {exp}_{p}^{*}:\text {H}^{1}(\mathbf {Q},V_{fgh})\rightarrow {\mathbf {Q}}_{p}$
is the composition of the restriction map
$\text {exp}_{p}^{*}:\text {H}^{1}(\mathbf {Q},V_{fgh})\rightarrow {\mathbf {Q}}_{p}$
is the composition of the restriction map
 $$ \begin{align*} \textrm{Loc}_{p}:\textrm{H}^{1}(\mathbf{Q},V_{fgh})\rightarrow\textrm{H}^{1}({\mathbf{Q}}_{p},V_{fgh}) \end{align*} $$
$$ \begin{align*} \textrm{Loc}_{p}:\textrm{H}^{1}(\mathbf{Q},V_{fgh})\rightarrow\textrm{H}^{1}({\mathbf{Q}}_{p},V_{fgh}) \end{align*} $$
with the dual exponential map of Bloch–Kato [Reference Bloch and Kato7] paired against a differential associated to
![]() $(f,g,h)$
. As a result, the class
$(f,g,h)$
. As a result, the class
![]() $\kappa _{\gamma ,\delta }(f,g,h)$
is crystalline at p and therefore lands in the Bloch–Kato Selmer group
$\kappa _{\gamma ,\delta }(f,g,h)$
is crystalline at p and therefore lands in the Bloch–Kato Selmer group
 $\text {Sel}(\mathbf {Q},V_{fgh})\subset \text {H}^{1}(\mathbf {Q},V_{fgh})$
, precisely when
$\text {Sel}(\mathbf {Q},V_{fgh})\subset \text {H}^{1}(\mathbf {Q},V_{fgh})$
, precisely when
![]() $L(s,f\otimes g\otimes h)$
vanishes at
$L(s,f\otimes g\otimes h)$
vanishes at
![]() $s=1$
. With the different choices for
$s=1$
. With the different choices for
![]() $\gamma $
and
$\gamma $
and
![]() $\delta $
, one thus obtains four – a priori distinct – classes
$\delta $
, one thus obtains four – a priori distinct – classes
![]() $\kappa _{\gamma ,\delta }(f,g,h)\in \text {Sel}(\mathbf {Q},V_{fgh})$
whenever
$\kappa _{\gamma ,\delta }(f,g,h)\in \text {Sel}(\mathbf {Q},V_{fgh})$
whenever
![]() $L(1,f\otimes g\otimes h)=0$
, and Darmon–Rotger conjectured (see [Reference Darmon and Rotger17, Conj. 3.2]) that the following are equivalent:
$L(1,f\otimes g\otimes h)=0$
, and Darmon–Rotger conjectured (see [Reference Darmon and Rotger17, Conj. 3.2]) that the following are equivalent:
-
(a) the classes
 $\kappa _{\gamma ,\delta }(f,g,h)$
span a nontrivial subspace of
$\kappa _{\gamma ,\delta }(f,g,h)$
span a nontrivial subspace of
 $\text {Sel}(\mathbf {Q},V_{fgh})$
,
$\text {Sel}(\mathbf {Q},V_{fgh})$
, -
(b)
 $\text {dim}_{{\mathbf {Q}}_{p}}\text {Sel}(\mathbf {Q},V_{fgh})=2$
,
$\text {dim}_{{\mathbf {Q}}_{p}}\text {Sel}(\mathbf {Q},V_{fgh})=2$
,
assuming for simplicity that the Hecke fields of f, g and h embed into
![]() ${\mathbf {Q}}_{p}$
.
${\mathbf {Q}}_{p}$
.
The adjoint rank
 $(2,0)$
setting
$(2,0)$
setting
The construction of
![]() $\kappa _{\gamma ,\delta }(f,g,h)$
yields classes with a bearing on the arithmetic of elliptic curves
$\kappa _{\gamma ,\delta }(f,g,h)$
yields classes with a bearing on the arithmetic of elliptic curves
![]() $E/\mathbf {Q}$
by taking f to be the newform associated to E and
$E/\mathbf {Q}$
by taking f to be the newform associated to E and
![]() $h=g^{*}$
to be the dual of g, so that the triple tensor product
$h=g^{*}$
to be the dual of g, so that the triple tensor product
![]() $V_{fgg^{*}}$
decomposes as
$V_{fgg^{*}}$
decomposes as
 $$ \begin{align} V_{fgg^{*}}\simeq V_{p}E\oplus\big(V_{p}E\otimes\textrm{ad}^{0}V_{p}(g)\big), \end{align} $$
$$ \begin{align} V_{fgg^{*}}\simeq V_{p}E\oplus\big(V_{p}E\otimes\textrm{ad}^{0}V_{p}(g)\big), \end{align} $$
where
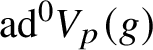 $\text {ad}^{0}V_{p}(g)$
is the 3-dimensional
$\text {ad}^{0}V_{p}(g)$
is the 3-dimensional
![]() $G_{\mathbf {Q}}$
-representation on the space of trace zero endomorphisms of
$G_{\mathbf {Q}}$
-representation on the space of trace zero endomorphisms of
![]() $V_{p}(g)$
. Correspondingly,
$V_{p}(g)$
. Correspondingly,
![]() $L(s,f\otimes g\otimes g^{*})$
factors as
$L(s,f\otimes g\otimes g^{*})$
factors as
In particular, the above construction yields the four generalised Kato classes
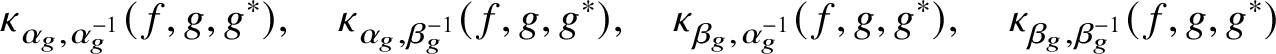 $$ \begin{align} \kappa_{\alpha_{g},\alpha_{g}^{-1}}(f,g,g^{*}),\quad\kappa_{\alpha_{g},\beta_{g}^{-1}}(f,g,g^{*}),\quad\kappa_{\beta_{g},\alpha_{g}^{-1}}(f,g,g^{*}),\quad\kappa_{\beta_{g},\beta_{g}^{-1}}(f,g,g^{*}) \end{align} $$
$$ \begin{align} \kappa_{\alpha_{g},\alpha_{g}^{-1}}(f,g,g^{*}),\quad\kappa_{\alpha_{g},\beta_{g}^{-1}}(f,g,g^{*}),\quad\kappa_{\beta_{g},\alpha_{g}^{-1}}(f,g,g^{*}),\quad\kappa_{\beta_{g},\beta_{g}^{-1}}(f,g,g^{*}) \end{align} $$
landing (thanks to the explicit reciprocity law (1.6)) in the Selmer group
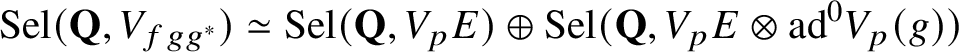 $$ \begin{align*} \textrm{Sel}(\mathbf{Q},V_{fgg^{*}})\simeq\textrm{Sel}(\mathbf{Q},V_{p}E)\oplus\textrm{Sel}(\mathbf{Q},V_{p}E\otimes\textrm{ad}^{0}V_{p}(g)) \end{align*} $$
$$ \begin{align*} \textrm{Sel}(\mathbf{Q},V_{fgg^{*}})\simeq\textrm{Sel}(\mathbf{Q},V_{p}E)\oplus\textrm{Sel}(\mathbf{Q},V_{p}E\otimes\textrm{ad}^{0}V_{p}(g)) \end{align*} $$
whenever
![]() $L(E,1)=0$
. Since one expects
$L(E,1)=0$
. Since one expects
 $L(E,\text {ad}^{0}(g),1)\neq 0\Longleftrightarrow \text {Sel}(\mathbf {Q},V_{p}E\otimes \text {ad}^{0}V_{p}(g))=0$
by the Bloch–Kato conjecture, the nonvanishing criterion in [Reference Darmon and Rotger17, Conj. 3.2] leads to the following prediction (see the ‘adjoint rank
$L(E,\text {ad}^{0}(g),1)\neq 0\Longleftrightarrow \text {Sel}(\mathbf {Q},V_{p}E\otimes \text {ad}^{0}V_{p}(g))=0$
by the Bloch–Kato conjecture, the nonvanishing criterion in [Reference Darmon and Rotger17, Conj. 3.2] leads to the following prediction (see the ‘adjoint rank
![]() $(2,0)$
setting’ discussed in [Reference Darmon and Rotger18, §4.5.3]).
$(2,0)$
setting’ discussed in [Reference Darmon and Rotger18, §4.5.3]).
Conjecture 1.2 Darmon–Rotger
Suppose that
![]() $L(E,s)$
has sign
$L(E,s)$
has sign
![]() $+1$
and vanishes at
$+1$
and vanishes at
![]() $s=1$
and that
$s=1$
and that
![]() $L(E,\mathrm {ad}^{0}(g),1)\neq 0$
. Then the following are equivalent:
$L(E,\mathrm {ad}^{0}(g),1)\neq 0$
. Then the following are equivalent:
-
(i) the four classes in
 $(1.8)$
span a nontrivial subspace of
$(1.8)$
span a nontrivial subspace of
 $\text {Sel}(\mathbf {Q},V_{p}E)$
.
$\text {Sel}(\mathbf {Q},V_{p}E)$
. -
(ii)
 $\text {dim}_{{\mathbf {Q}}_{p}}\text {Sel}(\mathbf {Q},V_{p}E)=2$
.
$\text {dim}_{{\mathbf {Q}}_{p}}\text {Sel}(\mathbf {Q},V_{p}E)=2$
.
Remark 1.3. Of course, by the Birch and Swinnerton-Dyer conjecture, condition (ii) in Conjecture 1.2 should be equivalent to the condition
![]() $\text {ord}_{s=1}L(E,s)=2$
.
$\text {ord}_{s=1}L(E,s)=2$
.
Remark 1.4. Note that Conjecture 1.2 does not predict that the four classes in (1.8) generate
![]() $\text {Sel}(\mathbf {Q},V_{p}E)$
. In fact, a strengthtening of the elliptic Stark conjectures in [Reference Darmon, Lauder and Rotger16] predicts that in the setting of Conjecture 1.2 only the classes
$\text {Sel}(\mathbf {Q},V_{p}E)$
. In fact, a strengthtening of the elliptic Stark conjectures in [Reference Darmon, Lauder and Rotger16] predicts that in the setting of Conjecture 1.2 only the classes
 $\kappa _{\alpha _{g},\alpha _{g}^{-1}}(f,g,g^{*})$
and
$\kappa _{\alpha _{g},\alpha _{g}^{-1}}(f,g,g^{*})$
and
 $\kappa _{\beta _{g},\beta _{g}^{-1}}(f,g,g^{*})$
are nonzero and that they are the same class up to a nonzero algebraic constant. Our results also confirm this prediction (see Remark 1.6 and Subsection 5.7 for further details).
$\kappa _{\beta _{g},\beta _{g}^{-1}}(f,g,g^{*})$
are nonzero and that they are the same class up to a nonzero algebraic constant. Our results also confirm this prediction (see Remark 1.6 and Subsection 5.7 for further details).
1.2 Statement of the main results
In this article, we prove Conjecture 1.2 in the case when the auxiliary eigenform g has complex multiplication, assuming
![]() (in fact, a weaker condition suffices) for one of the implications.
(in fact, a weaker condition suffices) for one of the implications.
As before, let
![]() $E/\mathbf {Q}$
be an elliptic curve with good ordinary reduction at
$E/\mathbf {Q}$
be an elliptic curve with good ordinary reduction at
![]() $p>3$
and let
$p>3$
and let
![]() $f\in S_{2}(\Gamma _{0}(N_{f}))$
be the associated newform. Let K be an imaginary quadratic field of discriminant prime of
$f\in S_{2}(\Gamma _{0}(N_{f}))$
be the associated newform. Let K be an imaginary quadratic field of discriminant prime of
![]() $N_{f}$
in which
$N_{f}$
in which
![]() $(p)={\mathfrak p}\overline {{\mathfrak p}}$
splits and let
$(p)={\mathfrak p}\overline {{\mathfrak p}}$
splits and let
![]() $\psi $
be a ray class character of K of conductor prime to
$\psi $
be a ray class character of K of conductor prime to
![]() $pN_{f}$
valued in a number field L. The weight 1 theta series
$pN_{f}$
valued in a number field L. The weight 1 theta series
![]() $g=\theta _{\psi }$
then satisfies
$g=\theta _{\psi }$
then satisfies
where
![]() $E^{K}$
is the twist of E by the quadratic character associated to K and
$E^{K}$
is the twist of E by the quadratic character associated to K and
![]() $\chi $
is the ring class character given by
$\chi $
is the ring class character given by
![]() $\psi /\psi ^{\tau }$
, for
$\psi /\psi ^{\tau }$
, for
![]() $\psi ^{\tau }$
the composition of
$\psi ^{\tau }$
the composition of
![]() $\psi $
with the action of complex conjugation
$\psi $
with the action of complex conjugation
![]() $\tau $
. In this case,
$\tau $
. In this case,
![]() $\alpha _{g}=\psi (\overline {\mathfrak {p}})$
and
$\alpha _{g}=\psi (\overline {\mathfrak {p}})$
and
![]() $\beta _{g}=\psi (\mathfrak {p})$
are the roots of the Hecke polynomial of g and p, which we shall simply denote by
$\beta _{g}=\psi (\mathfrak {p})$
are the roots of the Hecke polynomial of g and p, which we shall simply denote by
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
, respectively, and
$\beta $
, respectively, and
![]() $g^{*}$
is the theta series of
$g^{*}$
is the theta series of
![]() $\psi ^{-1}$
. As in the formulation of the conjectures in [Reference Darmon and Rotger17], we assume that
$\psi ^{-1}$
. As in the formulation of the conjectures in [Reference Darmon and Rotger17], we assume that
![]() $\alpha _{g}\neq \beta _{g}$
; that is,
$\alpha _{g}\neq \beta _{g}$
; that is,
![]() $\chi (\overline {{\mathfrak p}})\neq 1$
.
$\chi (\overline {{\mathfrak p}})\neq 1$
.
Let
![]() $\bar {\rho }_{E,p}:G_{\mathbf {Q}}\rightarrow \text {Aut}_{\mathbf {F}_{p}}(E[p])$
be the mod p representation associated to E and denote by
$\bar {\rho }_{E,p}:G_{\mathbf {Q}}\rightarrow \text {Aut}_{\mathbf {F}_{p}}(E[p])$
be the mod p representation associated to E and denote by
![]() $N_{f}^{-}$
the largest factor of
$N_{f}^{-}$
the largest factor of
![]() $N_{f}$
divisible only by primes that are inert in K. Finally, let
$N_{f}$
divisible only by primes that are inert in K. Finally, let
 $$ \begin{align*} \textrm{Loc}_{p}:\textrm{Sel}(\mathbf{Q},V_{p}E)\rightarrow\textrm{H}^{1}({\mathbf{Q}}_{p},V_{p}E) \end{align*} $$
$$ \begin{align*} \textrm{Loc}_{p}:\textrm{Sel}(\mathbf{Q},V_{p}E)\rightarrow\textrm{H}^{1}({\mathbf{Q}}_{p},V_{p}E) \end{align*} $$
be the restriction map at p.
Theorem A. Suppose that
![]() $L(E,s)$
has sign
$L(E,s)$
has sign
![]() $+1$
and vanishes at
$+1$
and vanishes at
![]() $s=1$
and that the value
$s=1$
and that the value
is nonzero. Suppose also that
-
•
 $\bar {\rho }_{E,p}$
is irreducible,
$\bar {\rho }_{E,p}$
is irreducible, -
•
 $N_{f}^{-}$
is the squarefree of an odd number of primes,
$N_{f}^{-}$
is the squarefree of an odd number of primes, -
•
 $\bar {\rho }_{E,p}$
is ramified at every prime
$\bar {\rho }_{E,p}$
is ramified at every prime
 $q\vert N_{f}^{-}$
.
$q\vert N_{f}^{-}$
.
Then
![]() $\kappa _{\alpha ,\beta ^{-1}}(f,g,g^{*})=\kappa _{\beta ,\alpha ^{-1}}(f,g,g^{*})=0$
and the following hold:
$\kappa _{\alpha ,\beta ^{-1}}(f,g,g^{*})=\kappa _{\beta ,\alpha ^{-1}}(f,g,g^{*})=0$
and the following hold:
and, conversely,
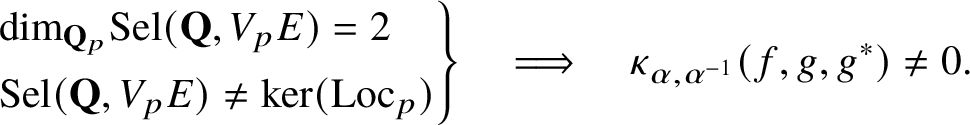
In particular, if
![]() $\mathrm{Sel}(\mathbf {Q},V_{p})\neq \mathrm{ker}(\mathrm{Loc}_{p})$
, then Conjecture 1.2 holds.
$\mathrm{Sel}(\mathbf {Q},V_{p})\neq \mathrm{ker}(\mathrm{Loc}_{p})$
, then Conjecture 1.2 holds.
Remark 1.5. The condition
![]() $\text {Sel}(\mathbf {Q},V_{p}E)\neq \text {ker}(\text {Loc}_{p})$
should always hold when
$\text {Sel}(\mathbf {Q},V_{p}E)\neq \text {ker}(\text {Loc}_{p})$
should always hold when
![]() $\text {Sel}(\mathbf {Q},V_{p}E)\neq 0$
. Indeed, if
$\text {Sel}(\mathbf {Q},V_{p}E)\neq 0$
. Indeed, if
![]() $\text {Sel}(\mathbf {Q},V_{p}E)$
equals
$\text {Sel}(\mathbf {Q},V_{p}E)$
equals
![]() $\text {ker}(\text {Loc}_{p})$
, then
$\text {ker}(\text {Loc}_{p})$
, then
![]() $E(\mathbf {Q})$
must be finite (since
$E(\mathbf {Q})$
must be finite (since
![]() $E(\mathbf {Q})$
injects into
$E(\mathbf {Q})$
injects into
![]() $E({\mathbf {Q}}_{p})$
), so if also
$E({\mathbf {Q}}_{p})$
), so if also
![]() $\text {Sel}(\mathbf {Q},V_{p}E)\neq 0$
, we would conclude that
$\text {Sel}(\mathbf {Q},V_{p}E)\neq 0$
, we would conclude that
![]() is infinite.
is infinite.
Remark 1.6. It also follows from our results that, for
![]() $g=\theta _{\psi }$
as above, the classes
$g=\theta _{\psi }$
as above, the classes
![]() $\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})$
and
$\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})$
and
![]() $\kappa _{\beta ,\beta ^{-1}}(f,g,g^{*})$
are the same up to a nonzero algebraic constant and they span the p-adic line
$\kappa _{\beta ,\beta ^{-1}}(f,g,g^{*})$
are the same up to a nonzero algebraic constant and they span the p-adic line
where
![]() $\text {log}_{p}:\text {Sel}(\mathbf {Q},V_{p}E)\rightarrow {\mathbf {Q}}_{p}$
is the composition of
$\text {log}_{p}:\text {Sel}(\mathbf {Q},V_{p}E)\rightarrow {\mathbf {Q}}_{p}$
is the composition of
![]() $\text {Loc}_{p}$
with the formal group logarithm of E. When
$\text {Loc}_{p}$
with the formal group logarithm of E. When
![]() , it is suggestive to view
, it is suggestive to view
![]() $\mathscr {L}_{p}$
as the line spanned by the image of
$\mathscr {L}_{p}$
as the line spanned by the image of
 $$ \begin{align*} P\wedge Q:=P\otimes Q-Q\otimes P\in \bigwedge^{2}(E(\mathbf{Q})\otimes\mathbf{Q}) \end{align*} $$
$$ \begin{align*} P\wedge Q:=P\otimes Q-Q\otimes P\in \bigwedge^{2}(E(\mathbf{Q})\otimes\mathbf{Q}) \end{align*} $$
under the natural map
 $$ \begin{align*} \textrm{Log}_{p}:\bigwedge^{2}(E(\mathbf{Q})\otimes\mathbf{Q})\rightarrow E(\mathbf{Q})\otimes{\mathbf{Q}}_{p} \end{align*} $$
$$ \begin{align*} \textrm{Log}_{p}:\bigwedge^{2}(E(\mathbf{Q})\otimes\mathbf{Q})\rightarrow E(\mathbf{Q})\otimes{\mathbf{Q}}_{p} \end{align*} $$
induced by
![]() $\text {log}_{p}$
. This is consistent with predictions by Darmon–Rotger (see [Reference Darmon and Rotger17, §4.5.3]) and suggests the view
$\text {log}_{p}$
. This is consistent with predictions by Darmon–Rotger (see [Reference Darmon and Rotger17, §4.5.3]) and suggests the view
![]() $\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})$
as a ‘p-adic shadow’ of a rank 2 motivic regulator.
$\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})$
as a ‘p-adic shadow’ of a rank 2 motivic regulator.
Remark 1.7. Note that the implications (1.9) and (1.10) in Theorem A are rank 2 analogues of the implications (1.2) and (1.3) by Kolyvagin and Skinner, respectively.
The key new ingredient in the proof of Theorem A is a leading term formula for an anticyclotomic p-adic L-function
![]() attached to
attached to
![]() $E/K$
in terms of anticyclotomic derived p-adic heights (see Theorem 5.3). This formula applies in arbitrary order of vanishing of
$E/K$
in terms of anticyclotomic derived p-adic heights (see Theorem 5.3). This formula applies in arbitrary order of vanishing of
![]() $\Theta _{f/K}$
at
$\Theta _{f/K}$
at
![]() $T=0$
and, in particular, it allows us to deduce the following p-adic analytic criterion for the nonvanishing of generalised Kato classes.
$T=0$
and, in particular, it allows us to deduce the following p-adic analytic criterion for the nonvanishing of generalised Kato classes.
Theorem B. Under the hypotheses of Theorem A, assume in addition that
![]() $\mathrm{rank}_{\mathbf {Z}}E(\mathbf {Q})>0$
. Then the following implication holds:
$\mathrm{rank}_{\mathbf {Z}}E(\mathbf {Q})>0$
. Then the following implication holds:
The same result holds with
![]() $\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})$
replaced by
$\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})$
replaced by
![]() $\kappa _{\beta ,\beta ^{-1}}(f,g,g^{*})$
.
$\kappa _{\beta ,\beta ^{-1}}(f,g,g^{*})$
.
Remark 1.8. If
![]() $\bar {\rho }_{E,p}$
is irreducible and ramified at some prime
$\bar {\rho }_{E,p}$
is irreducible and ramified at some prime
![]() $q\neq p$
(e.g., if E is semistable and
$q\neq p$
(e.g., if E is semistable and
![]() $p\geqslant 11$
is good ordinary for E, by [Reference Ribet39] and [Reference Mazur33]), the nonvanishing results of [Reference Bump, Friedberg and Hoffstein9] and [Reference Vatsal48] assure the existence of infinitely many imaginary quadratic fields K and ring class characters
$p\geqslant 11$
is good ordinary for E, by [Reference Ribet39] and [Reference Mazur33]), the nonvanishing results of [Reference Bump, Friedberg and Hoffstein9] and [Reference Vatsal48] assure the existence of infinitely many imaginary quadratic fields K and ring class characters
![]() $\chi $
such that
$\chi $
such that
-
• q is inert in K,
-
• every prime factor of
 $N_{f}/q$
splits in K,
$N_{f}/q$
splits in K, -
•
 $L(E,\text {ad}^{0}(g),1)=L(E^{K},1)\cdot L(E/K,\chi ,1)\neq 0$
.
$L(E,\text {ad}^{0}(g),1)=L(E^{K},1)\cdot L(E/K,\chi ,1)\neq 0$
.
Thus, Theorem B suggests a general construction of nontrivial p-adic Selmer classes for rational elliptic curves of rank 2.
Remark 1.9. In the Appendix to this article, we apply Theorem B to numerically verify the nonvanishing of generalised Kato classes for specific rational elliptic curves of algebraic and analytic rank 2, a task that was left as ‘an interesting challenge’ by Darmon–Rotger (see [Reference Darmon and Rotger17, p. 31]).
Remark 1.10. Assume that
![]() $\text {rank}_{\mathbf {Z}}E(\mathbf {Q})=2$
and
$\text {rank}_{\mathbf {Z}}E(\mathbf {Q})=2$
and
![]() . A refinement of Conjecture 1.2 predicting the position of
. A refinement of Conjecture 1.2 predicting the position of
![]() $\kappa _{\gamma ,\delta }(f,g,g^{*})$
relative to the natural rational structure on
$\kappa _{\gamma ,\delta }(f,g,g^{*})$
relative to the natural rational structure on
![]() $\text {Sel}(\mathbf {Q},V_{p}E)=E(\mathbf {Q})\otimes {\mathbf {Q}}_{p}$
then leads to the expectation
$\text {Sel}(\mathbf {Q},V_{p}E)=E(\mathbf {Q})\otimes {\mathbf {Q}}_{p}$
then leads to the expectation
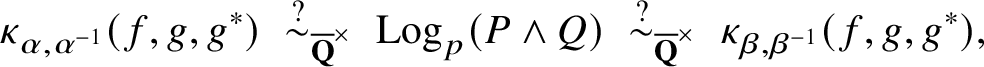 $$ \begin{align} \kappa_{\alpha,\alpha^{-1}}(f,g,g^{*})\;\overset{?}\sim_{\overline{\mathbf{Q}}^{\times}}\;\textrm{Log}_{p}(P\wedge Q)\;\overset{?}\sim_{\overline{\mathbf{Q}}^{\times}}\;\kappa_{\beta,\beta^{-1}}(f,g,g^{*}), \end{align} $$
$$ \begin{align} \kappa_{\alpha,\alpha^{-1}}(f,g,g^{*})\;\overset{?}\sim_{\overline{\mathbf{Q}}^{\times}}\;\textrm{Log}_{p}(P\wedge Q)\;\overset{?}\sim_{\overline{\mathbf{Q}}^{\times}}\;\kappa_{\beta,\beta^{-1}}(f,g,g^{*}), \end{align} $$
where
![]() $(P, Q)$
is any basis for
$(P, Q)$
is any basis for
![]() $E(\mathbf {Q})\otimes \mathbf {Q}$
and
$E(\mathbf {Q})\otimes \mathbf {Q}$
and
![]() $\sim _{\overline {\mathbf {Q}}^{\times }}$
denotes equality up to multiplication by a nonzero algebraic number. Our results confirm the predicted relation
$\sim _{\overline {\mathbf {Q}}^{\times }}$
denotes equality up to multiplication by a nonzero algebraic number. Our results confirm the predicted relation
 $\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})\sim _{\overline {\mathbf {Q}}^{\times }}\kappa _{\beta ,\beta ^{-1}}(f,g,g^{*})$
, and in Theorem 5.5 we show that
$\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})\sim _{\overline {\mathbf {Q}}^{\times }}\kappa _{\beta ,\beta ^{-1}}(f,g,g^{*})$
, and in Theorem 5.5 we show that
 $$ \begin{align*} \kappa_{\alpha,\alpha^{-1}}(f,g,g^{*})\sim_{\mathbf{Q}^{\times}}C\cdot \frac{1-p^{-1}\alpha_{p}}{1-\alpha_{p}^{-1}}\cdot\frac{\Theta_{f/K}^{(\mathfrak{r})}}{h_{p}^{(\mathfrak{r})}(P,Q)}\cdot\textrm{Log}_{p}(P\wedge Q), \nonumber \end{align*} $$
$$ \begin{align*} \kappa_{\alpha,\alpha^{-1}}(f,g,g^{*})\sim_{\mathbf{Q}^{\times}}C\cdot \frac{1-p^{-1}\alpha_{p}}{1-\alpha_{p}^{-1}}\cdot\frac{\Theta_{f/K}^{(\mathfrak{r})}}{h_{p}^{(\mathfrak{r})}(P,Q)}\cdot\textrm{Log}_{p}(P\wedge Q), \nonumber \end{align*} $$
where C is a nonzero algebraic number,
![]() $\alpha _{p}$
is the p-adic unit root of
$\alpha _{p}$
is the p-adic unit root of
![]() $x^{2}-a_{p}(E)x+p$
(with
$x^{2}-a_{p}(E)x+p$
(with
![]() $a_{p}(E)=p+1-\#E(\mathbf {F}_{p})$
as usual),
$a_{p}(E)=p+1-\#E(\mathbf {F}_{p})$
as usual),
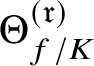 $\Theta _{f/K}^{(\mathfrak {r})}$
is the leading term of
$\Theta _{f/K}^{(\mathfrak {r})}$
is the leading term of
![]() $\Theta _{f/K}$
at
$\Theta _{f/K}$
at
![]() $T=0$
and
$T=0$
and
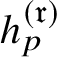 $h_{p}^{(\mathfrak {r})}$
is the anticyclotomic
$h_{p}^{(\mathfrak {r})}$
is the anticyclotomic
![]() $\mathfrak {r}$
th derived p-adic height pairing. In particular, this implies that the conjectured algebraicity in
$\mathfrak {r}$
th derived p-adic height pairing. In particular, this implies that the conjectured algebraicity in
![]() $(1.11)$
follows from a p-adic Birch and Swinnerton-Dyer conjecture refining [Reference Bertolini and Darmon4, Conj. 4.3] (see Subsection 5.7).
$(1.11)$
follows from a p-adic Birch and Swinnerton-Dyer conjecture refining [Reference Bertolini and Darmon4, Conj. 4.3] (see Subsection 5.7).
1.3 Relation to previous work
Prior to this article, the only general results (known to the authors) on the existence on nonzero Selmer classes for elliptic curves
![]() $E/\mathbf {Q}$
of rank
$E/\mathbf {Q}$
of rank
![]() $r>1$
are in forthcoming work of Skinner–Urban (see [Reference Urban47] for a report). Their methods, which extend those outlined in their ICM address [Reference Skinner and Urban44] for cuspidal eigenforms of weight
$r>1$
are in forthcoming work of Skinner–Urban (see [Reference Urban47] for a report). Their methods, which extend those outlined in their ICM address [Reference Skinner and Urban44] for cuspidal eigenforms of weight
![]() $k\geqslant 4$
, are completely different from ours.
$k\geqslant 4$
, are completely different from ours.
On the other hand, Darmon–Rotger [Reference Darmon and Rotger18] exhibited, under a certain nonvanishing hypothesis, the existence of two linearly independent classes in the Selmer groups
![]() $\text {Sel}(\mathbf {Q},V_{p}E\otimes \varrho )$
of elliptic curves
$\text {Sel}(\mathbf {Q},V_{p}E\otimes \varrho )$
of elliptic curves
![]() $E/\mathbf {Q}$
twisted by degree 4 Artin representations
$E/\mathbf {Q}$
twisted by degree 4 Artin representations
![]() $\varrho $
. The required nonvanishing is that of a special value
$\varrho $
. The required nonvanishing is that of a special value
 $\mathscr {L}_{p}^{g_{\alpha }}$
of a certain p-adic L-function. Both their works and ours exploit the construction of generalised Kato classes introduced in [Reference Darmon and Rotger18], but in the setting we have placed ourselves in, the special value
$\mathscr {L}_{p}^{g_{\alpha }}$
of a certain p-adic L-function. Both their works and ours exploit the construction of generalised Kato classes introduced in [Reference Darmon and Rotger18], but in the setting we have placed ourselves in, the special value
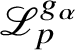 $\mathscr {L}_{p}^{g_{\alpha }}$
vanishes. The proofs of our main results are based on anticyclotomic Iwasawa theory and derived p-adic heights, both of which make no appearance in [Reference Darmon and Rotger18].
$\mathscr {L}_{p}^{g_{\alpha }}$
vanishes. The proofs of our main results are based on anticyclotomic Iwasawa theory and derived p-adic heights, both of which make no appearance in [Reference Darmon and Rotger18].
2 Triple products and theta elements
In this section we describe the triple product p-adic L-function for Hida families [Reference Hsieh28] and recall its relation with the square-root anticyclotomic p-adic L-functions of Bertolini–Darmon [Reference Bertolini and Darmon4].
2.1 Ordinary
 $\Lambda $
-adic forms
$\Lambda $
-adic forms
Fix a prime
![]() $p>2$
. Let
$p>2$
. Let
![]() $\mathbb {I}$
be a normal domain finite flat over
$\mathbb {I}$
be a normal domain finite flat over
![]() , where
, where
![]() $\mathcal O$
is the ring of integers of a finite extension
$\mathcal O$
is the ring of integers of a finite extension
![]() $L/{\mathbf {Q}}_{p}$
. We say that a point
$L/{\mathbf {Q}}_{p}$
. We say that a point
 $x\in \text {Spec}\;\mathbb {I}(\overline {\mathbf {Q}}_{p})$
is locally algebraic if its restriction to
$x\in \text {Spec}\;\mathbb {I}(\overline {\mathbf {Q}}_{p})$
is locally algebraic if its restriction to
![]() $1+p\mathbf {Z}_{p}$
is given by
$1+p\mathbf {Z}_{p}$
is given by
![]() $x(\gamma )=\gamma ^{k_{x}}\epsilon _{x}(\gamma )$
for some integer
$x(\gamma )=\gamma ^{k_{x}}\epsilon _{x}(\gamma )$
for some integer
![]() $k_{x}$
, called the weight of x and some finite-order character
$k_{x}$
, called the weight of x and some finite-order character
![]() $\epsilon _{x}:1+p\mathbf {Z}_{p}\rightarrow \mu _{p^{\infty }}$
; we say that x is arithmetic if it has weight
$\epsilon _{x}:1+p\mathbf {Z}_{p}\rightarrow \mu _{p^{\infty }}$
; we say that x is arithmetic if it has weight
![]() $k_{x}\geqslant 2$
. Let
$k_{x}\geqslant 2$
. Let
![]() $\mathfrak {X}_{\mathbb {I}}^{+}$
be the set of arithmetic points.
$\mathfrak {X}_{\mathbb {I}}^{+}$
be the set of arithmetic points.
Fix a positive integer N prime to p and let
![]() $\chi :(\mathbf {Z}/Np\mathbf {Z})^{\times }\rightarrow \mathcal O^{\times }$
be a Dirichlet character modulo
$\chi :(\mathbf {Z}/Np\mathbf {Z})^{\times }\rightarrow \mathcal O^{\times }$
be a Dirichlet character modulo
![]() $Np$
. Let
$Np$
. Let
![]() $S^{o}(N,\chi ,\mathbb {I})$
be the space of ordinary
$S^{o}(N,\chi ,\mathbb {I})$
be the space of ordinary
![]() $\mathbb {I}$
-adic cusp forms of tame level N and branch character
$\mathbb {I}$
-adic cusp forms of tame level N and branch character
![]() $\chi $
, consisting of formal power series
$\chi $
, consisting of formal power series
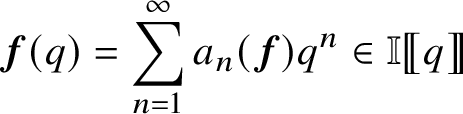
such that for every
![]() $x\in \mathfrak {X}_{\mathbb {I}}^{+}$
the specialisation
$x\in \mathfrak {X}_{\mathbb {I}}^{+}$
the specialisation
![]() $\boldsymbol {f}_{x}(q)$
is the q-expansion of a p-ordinary cusp form
$\boldsymbol {f}_{x}(q)$
is the q-expansion of a p-ordinary cusp form
![]() $\boldsymbol {f}_{x}\in S_{k_{x}}(Np^{r_{x}+1},\chi \omega ^{2-k_{x}}\epsilon _{x})$
. Here
$\boldsymbol {f}_{x}\in S_{k_{x}}(Np^{r_{x}+1},\chi \omega ^{2-k_{x}}\epsilon _{x})$
. Here
![]() $r_{x}$
is such that
$r_{x}$
is such that
![]() $\epsilon _{x}(1+p)$
has exact order
$\epsilon _{x}(1+p)$
has exact order
![]() $p^{r_{x}}$
and
$p^{r_{x}}$
and
![]() $\omega :(\mathbf {Z}/p\mathbf {Z})^{\times }\rightarrow \mu _{p-1}$
is the Teichmüller character.
$\omega :(\mathbf {Z}/p\mathbf {Z})^{\times }\rightarrow \mu _{p-1}$
is the Teichmüller character.
We say that
![]() $\boldsymbol {f}\in S^{o}(N,\chi ,\mathbb {I})$
is a primitive Hida family if for every
$\boldsymbol {f}\in S^{o}(N,\chi ,\mathbb {I})$
is a primitive Hida family if for every
![]() $x\in \mathfrak {X}_{\mathbb {I}}^{+}$
we have that
$x\in \mathfrak {X}_{\mathbb {I}}^{+}$
we have that
![]() $\boldsymbol {f}_{x}$
is an ordinary p-stabilised newform (in the sense of [Reference Hsieh28, Def. 2.4]) of tame level N. Given a primitive Hida family
$\boldsymbol {f}_{x}$
is an ordinary p-stabilised newform (in the sense of [Reference Hsieh28, Def. 2.4]) of tame level N. Given a primitive Hida family
![]() ${\boldsymbol {f}}\in S^{o}(N,\chi ,\mathbb {I})$
and writing
${\boldsymbol {f}}\in S^{o}(N,\chi ,\mathbb {I})$
and writing
![]() $\chi =\chi ^{\prime }\chi _{p}$
with
$\chi =\chi ^{\prime }\chi _{p}$
with
![]() $\chi ^{\prime }$
(respectively
$\chi ^{\prime }$
(respectively
![]() $\chi _{p}$
) a Dirichlet modulo N (respectively p), there is a primitive Hida family
$\chi _{p}$
) a Dirichlet modulo N (respectively p), there is a primitive Hida family
![]() ${{\boldsymbol {f}}}^{\iota }\in S^{o}(N,\chi _{p}\overline {\chi }^{\prime },\mathbb {I})$
with Fourier coefficients
${{\boldsymbol {f}}}^{\iota }\in S^{o}(N,\chi _{p}\overline {\chi }^{\prime },\mathbb {I})$
with Fourier coefficients
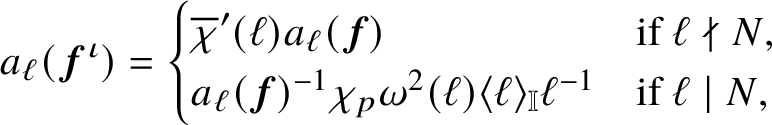 $$ \begin{align*} a_{\ell}({{\boldsymbol{f}}}^{\iota})= \begin{cases} \overline{\chi}^{\prime}(\ell)a_{\ell}({\boldsymbol{f}})&\mbox{if }\ell \nmid N{,}\\ a_{\ell}({\boldsymbol{f}})^{-1}\chi_{p}\omega^{2}(\ell)\langle\ell\rangle_{\mathbb{I}}\ell^{-1}& \mbox{if }\ell\mid N{,} \end{cases} \\[-15pt]\end{align*} $$
$$ \begin{align*} a_{\ell}({{\boldsymbol{f}}}^{\iota})= \begin{cases} \overline{\chi}^{\prime}(\ell)a_{\ell}({\boldsymbol{f}})&\mbox{if }\ell \nmid N{,}\\ a_{\ell}({\boldsymbol{f}})^{-1}\chi_{p}\omega^{2}(\ell)\langle\ell\rangle_{\mathbb{I}}\ell^{-1}& \mbox{if }\ell\mid N{,} \end{cases} \\[-15pt]\end{align*} $$
having the property that for every
![]() $x\in \mathfrak {X}_{\mathbb {I}}^{+}$
the specialisation
$x\in \mathfrak {X}_{\mathbb {I}}^{+}$
the specialisation
![]() ${{\boldsymbol {f}}}^{\iota }_{x}$
is the p-stabilised newform attached to the character twist
${{\boldsymbol {f}}}^{\iota }_{x}$
is the p-stabilised newform attached to the character twist
![]() ${\boldsymbol {f}}_{x}\otimes \overline {\chi }^{\prime }$
.
${\boldsymbol {f}}_{x}\otimes \overline {\chi }^{\prime }$
.
By [Reference Hida24] (cf. [Reference Wiles50, Thm. 2.2.1]), attached to every primitive Hida family
![]() ${\boldsymbol {f}}\in S^{o}(N,\chi ,\mathbb {I})$
there is a continuous
${\boldsymbol {f}}\in S^{o}(N,\chi ,\mathbb {I})$
there is a continuous
![]() $\mathbb {I}$
-adic representation
$\mathbb {I}$
-adic representation
![]() $\rho _{\boldsymbol {f}}:G_{\mathbf {Q}}\rightarrow \text {GL}_{2}(\text {Frac}\,\mathbb {I})$
which is unramified outside
$\rho _{\boldsymbol {f}}:G_{\mathbf {Q}}\rightarrow \text {GL}_{2}(\text {Frac}\,\mathbb {I})$
which is unramified outside
![]() $Np$
and such that for every prime
$Np$
and such that for every prime
![]() $\ell \nmid Np$
,
$\ell \nmid Np$
,
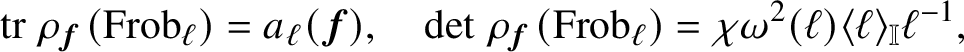 $$ \begin{align*} \textrm{tr}\;\rho_{\boldsymbol{f}}(\textrm{Frob}_{\ell})=a_{\ell}({\boldsymbol{f}}), \quad \textrm{det}\;\rho_{{\boldsymbol{f}}}(\textrm{Frob}_{\ell})=\chi\omega^{2}(\ell)\langle\ell\rangle_{\mathbb{I}}\ell^{-1}, \\[-15pt]\end{align*} $$
$$ \begin{align*} \textrm{tr}\;\rho_{\boldsymbol{f}}(\textrm{Frob}_{\ell})=a_{\ell}({\boldsymbol{f}}), \quad \textrm{det}\;\rho_{{\boldsymbol{f}}}(\textrm{Frob}_{\ell})=\chi\omega^{2}(\ell)\langle\ell\rangle_{\mathbb{I}}\ell^{-1}, \\[-15pt]\end{align*} $$
where
![]() $\langle \ell \rangle _{\mathbb {I}}\in \mathbb {I}^{\times }$
is the image of
$\langle \ell \rangle _{\mathbb {I}}\in \mathbb {I}^{\times }$
is the image of
![]() $\langle \ell \rangle :=\ell \omega ^{-1}(\ell )\in 1+p\mathbf {Z}_{p}$
under the natural map
$\langle \ell \rangle :=\ell \omega ^{-1}(\ell )\in 1+p\mathbf {Z}_{p}$
under the natural map
In particular, letting
![]() $\langle \varepsilon _{\text {cyc}}\rangle _{\mathbb {I}}:G_{\mathbf {Q}}\rightarrow \mathbb {I}^{\times }$
be defined by
$\langle \varepsilon _{\text {cyc}}\rangle _{\mathbb {I}}:G_{\mathbf {Q}}\rightarrow \mathbb {I}^{\times }$
be defined by
![]() $\langle \varepsilon _{\text {cyc}}\rangle _{\mathbb {I}}(\sigma )=\langle \varepsilon _{\text {cyc}}(\sigma )\rangle _{\mathbb {I}}$
, it follows that
$\langle \varepsilon _{\text {cyc}}\rangle _{\mathbb {I}}(\sigma )=\langle \varepsilon _{\text {cyc}}(\sigma )\rangle _{\mathbb {I}}$
, it follows that
![]() $\rho _{\boldsymbol {f}}$
has determinant
$\rho _{\boldsymbol {f}}$
has determinant
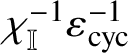 $\chi _{\mathbb {I}}^{-1}\varepsilon _{\text {cyc}}^{-1}$
, where
$\chi _{\mathbb {I}}^{-1}\varepsilon _{\text {cyc}}^{-1}$
, where
![]() $\chi _{\mathbb {I}}:G_{\mathbf {Q}}\rightarrow \mathbb {I}^{\times }$
is given by
$\chi _{\mathbb {I}}:G_{\mathbf {Q}}\rightarrow \mathbb {I}^{\times }$
is given by
![]() $\chi _{\mathbb {I}}:=\sigma _{\chi }\langle \varepsilon _{\text {cyc}}\rangle ^{-2}\langle \varepsilon _{\text {cyc}}\rangle _{\mathbb {I}}$
, with
$\chi _{\mathbb {I}}:=\sigma _{\chi }\langle \varepsilon _{\text {cyc}}\rangle ^{-2}\langle \varepsilon _{\text {cyc}}\rangle _{\mathbb {I}}$
, with
![]() $\sigma _{\chi }$
the Galois character sending
$\sigma _{\chi }$
the Galois character sending
![]() $\text {Frob}_{\ell }\mapsto \chi (\ell )^{-1}$
. Moreover, by [Reference Wiles50, Thm. 2.2.2], the restriction of
$\text {Frob}_{\ell }\mapsto \chi (\ell )^{-1}$
. Moreover, by [Reference Wiles50, Thm. 2.2.2], the restriction of
![]() $\rho _{\boldsymbol {f}}$
to
$\rho _{\boldsymbol {f}}$
to
![]() $G_{{\mathbf {Q}}_{p}}$
is given by
$G_{{\mathbf {Q}}_{p}}$
is given by
 $$ \begin{align} \rho_{{\boldsymbol{f}}}\vert_{G_{{\mathbf{Q}}_{p}}}\sim\left(\begin{array}{cc}\psi_{\boldsymbol{f}}&*\\ 0&\psi_{{\boldsymbol{f}}}^{-1}\chi_{\mathbb{I}}^{-1}\varepsilon_{\textrm{cyc}}^{-1}\end{array}\right),\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} \rho_{{\boldsymbol{f}}}\vert_{G_{{\mathbf{Q}}_{p}}}\sim\left(\begin{array}{cc}\psi_{\boldsymbol{f}}&*\\ 0&\psi_{{\boldsymbol{f}}}^{-1}\chi_{\mathbb{I}}^{-1}\varepsilon_{\textrm{cyc}}^{-1}\end{array}\right),\\[-15pt]\nonumber \end{align} $$
where
![]() $\psi _{{\boldsymbol {f}}}:G_{{\mathbf {Q}}_{p}}\rightarrow \mathbb {I}^{\times }$
is the unramified character with
$\psi _{{\boldsymbol {f}}}:G_{{\mathbf {Q}}_{p}}\rightarrow \mathbb {I}^{\times }$
is the unramified character with
![]() $\psi _{\boldsymbol {f}}(\text {Frob}_{p})=a_{p}({\boldsymbol {f}})$
.
$\psi _{\boldsymbol {f}}(\text {Frob}_{p})=a_{p}({\boldsymbol {f}})$
.
Let
![]() $T^{o}(N,\chi ,\mathbb {I})$
be the
$T^{o}(N,\chi ,\mathbb {I})$
be the
![]() $\mathbb {I}$
-algebra generated by Hecke operators acting on
$\mathbb {I}$
-algebra generated by Hecke operators acting on
![]() $S^{0}(N,\chi ,\mathbb {I})$
, and let
$S^{0}(N,\chi ,\mathbb {I})$
, and let
![]() $\lambda _{\boldsymbol f}:T^{o}(N,\chi ,\mathbb {I})\to \mathbb {I}$
be the
$\lambda _{\boldsymbol f}:T^{o}(N,\chi ,\mathbb {I})\to \mathbb {I}$
be the
![]() $\mathbb {I}$
-algebra homomorphism induced by
$\mathbb {I}$
-algebra homomorphism induced by
![]() ${\boldsymbol f}$
. Let
${\boldsymbol f}$
. Let
![]() $C(\lambda _{\boldsymbol {f}})$
be the congruence module associated with
$C(\lambda _{\boldsymbol {f}})$
be the congruence module associated with
![]() $\lambda _{\boldsymbol f}$
(see [Reference Hida25]). Under the following hypothesis:
$\lambda _{\boldsymbol f}$
(see [Reference Hida25]). Under the following hypothesis:
it follows from results of Hida and Wiles that
![]() $C(\lambda _{\boldsymbol {f}})$
is isomorphic to
$C(\lambda _{\boldsymbol {f}})$
is isomorphic to
![]() $\mathbb {I}/(\eta _{{\boldsymbol {f}}})$
for some nonzero
$\mathbb {I}/(\eta _{{\boldsymbol {f}}})$
for some nonzero
![]() $\eta _{\boldsymbol {f}}\in \mathbb {I}$
.
$\eta _{\boldsymbol {f}}\in \mathbb {I}$
.
2.2 Triple product p-adic L-function
Let
be a triple of primitive Hida families. Set
which is a finite extension of the three-variable Iwasawa algebra
![]() $\mathcal {R}_{0}:=\Lambda \hat {\otimes }_{\mathcal O}\Lambda \hat {\otimes }_{\mathcal O} \Lambda $
, and define the weight space
$\mathcal {R}_{0}:=\Lambda \hat {\otimes }_{\mathcal O}\Lambda \hat {\otimes }_{\mathcal O} \Lambda $
, and define the weight space
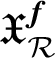 $\mathfrak {X}_{\mathcal {R}}^{\boldsymbol {f}}$
for the triple
$\mathfrak {X}_{\mathcal {R}}^{\boldsymbol {f}}$
for the triple
![]() $({\boldsymbol {f}},{\boldsymbol {g}},{\boldsymbol {h}})$
in the
$({\boldsymbol {f}},{\boldsymbol {g}},{\boldsymbol {h}})$
in the
![]() ${\boldsymbol {f}}$
-dominated unbalanced range by
${\boldsymbol {f}}$
-dominated unbalanced range by
 $$ \begin{align} \mathfrak{X}_{\mathcal{R}}^{\boldsymbol{f}}:=\left\{ (x,y,z)\in\mathfrak{X}_{\mathbb{I}_{\boldsymbol{f}}}^{+}\times\mathfrak{X}_{\mathbb{I}_{\boldsymbol{g}}}^{\textrm{cls}}\times\mathfrak{X}_{\mathbb{I}_{\boldsymbol{h}}}^{\textrm{cls}}\;\colon\;k_{x}\geqslant k_{y}+k_{z}\;\textrm{and}\;k_{x}\equiv k_{y}+k_{z}\;(\textrm{mod}\;2)\right\}, \end{align} $$
$$ \begin{align} \mathfrak{X}_{\mathcal{R}}^{\boldsymbol{f}}:=\left\{ (x,y,z)\in\mathfrak{X}_{\mathbb{I}_{\boldsymbol{f}}}^{+}\times\mathfrak{X}_{\mathbb{I}_{\boldsymbol{g}}}^{\textrm{cls}}\times\mathfrak{X}_{\mathbb{I}_{\boldsymbol{h}}}^{\textrm{cls}}\;\colon\;k_{x}\geqslant k_{y}+k_{z}\;\textrm{and}\;k_{x}\equiv k_{y}+k_{z}\;(\textrm{mod}\;2)\right\}, \end{align} $$
where
 $\mathfrak {X}_{\mathbb {I}_{{\boldsymbol {g}}}}^{\text {cls}}\supseteq \mathfrak {X}_{\mathbb {I}_{{\boldsymbol {g}}}}^{+}$
(and, similarly,
$\mathfrak {X}_{\mathbb {I}_{{\boldsymbol {g}}}}^{\text {cls}}\supseteq \mathfrak {X}_{\mathbb {I}_{{\boldsymbol {g}}}}^{+}$
(and, similarly,
 $\mathfrak {X}_{\mathbb {I}_{{\boldsymbol {h}}}}^{\text {cls}}$
) is the set of locally algebraic points in
$\mathfrak {X}_{\mathbb {I}_{{\boldsymbol {h}}}}^{\text {cls}}$
) is the set of locally algebraic points in
 $\text {Spec}\,{\mathbb {I}_{\boldsymbol {g}}}(\overline {\mathbf {Q}}_{p})$
for which
$\text {Spec}\,{\mathbb {I}_{\boldsymbol {g}}}(\overline {\mathbf {Q}}_{p})$
for which
![]() ${\boldsymbol {g}}_{x}(q)$
is the q-expansion of a classical modular form.
${\boldsymbol {g}}_{x}(q)$
is the q-expansion of a classical modular form.
For
![]() $\boldsymbol {\phi }\in \{{\boldsymbol {f}},{\boldsymbol {g}},{\boldsymbol {h}}\}$
and a positive integer N prime to p and divisible by
$\boldsymbol {\phi }\in \{{\boldsymbol {f}},{\boldsymbol {g}},{\boldsymbol {h}}\}$
and a positive integer N prime to p and divisible by
![]() $N_{\boldsymbol {\phi }}$
, define the space of
$N_{\boldsymbol {\phi }}$
, define the space of
![]() $\Lambda $
-adic test vectors
$\Lambda $
-adic test vectors
![]() $S^{o}(N,\chi _{\boldsymbol {\phi }},\mathbb {I}_{\boldsymbol {\phi }})[\boldsymbol {\phi }]$
of level N to be the
$S^{o}(N,\chi _{\boldsymbol {\phi }},\mathbb {I}_{\boldsymbol {\phi }})[\boldsymbol {\phi }]$
of level N to be the
![]() $\mathbb {I}_{\boldsymbol {\phi }}$
-submodule of
$\mathbb {I}_{\boldsymbol {\phi }}$
-submodule of
![]() $S^{o}(N,\chi _{\boldsymbol {\phi }},\mathbb {I}_{\boldsymbol {\phi }})$
generated by
$S^{o}(N,\chi _{\boldsymbol {\phi }},\mathbb {I}_{\boldsymbol {\phi }})$
generated by
![]() $\{\boldsymbol {\phi }(q^{d})\}$
as d ranges over the positive divisors of
$\{\boldsymbol {\phi }(q^{d})\}$
as d ranges over the positive divisors of
![]() $N/N_{\boldsymbol {\phi }}$
.
$N/N_{\boldsymbol {\phi }}$
.
For the next result, set
![]() $N:=\text {lcm}(N_{\boldsymbol {f}},N_{\boldsymbol {g}},N_{\boldsymbol {h}})$
and consider the following hypothesis:
$N:=\text {lcm}(N_{\boldsymbol {f}},N_{\boldsymbol {g}},N_{\boldsymbol {h}})$
and consider the following hypothesis:
 $$\begin{align*}\mbox{for some }(x,y,z)\in\mathfrak{X}_{\mathcal{R}}^{\boldsymbol{f}}\mbox{, we have }\varepsilon_{q}({\boldsymbol{f}}_{x}^{\circ},{\boldsymbol{g}}_{y}^{\circ},{\boldsymbol{h}}_{z}^{\circ})=+1\mbox{ for all }q\vert N\textrm{,} \end{align*}$$
$$\begin{align*}\mbox{for some }(x,y,z)\in\mathfrak{X}_{\mathcal{R}}^{\boldsymbol{f}}\mbox{, we have }\varepsilon_{q}({\boldsymbol{f}}_{x}^{\circ},{\boldsymbol{g}}_{y}^{\circ},{\boldsymbol{h}}_{z}^{\circ})=+1\mbox{ for all }q\vert N\textrm{,} \end{align*}$$
where
![]() $\varepsilon _{q}({\boldsymbol {f}}_{x}^{\circ },{\boldsymbol {g}}_{y}^{\circ },{\boldsymbol {h}}_{z}^{\circ })$
is the local root number at q of the Kummer self-dual twist of the tensor product of the p-adic Galois representations attached to the newforms
$\varepsilon _{q}({\boldsymbol {f}}_{x}^{\circ },{\boldsymbol {g}}_{y}^{\circ },{\boldsymbol {h}}_{z}^{\circ })$
is the local root number at q of the Kummer self-dual twist of the tensor product of the p-adic Galois representations attached to the newforms
![]() ${\boldsymbol {f}}_{x}^{\circ }$
,
${\boldsymbol {f}}_{x}^{\circ }$
,
![]() ${\boldsymbol {g}}_{y}^{\circ }$
and
${\boldsymbol {g}}_{y}^{\circ }$
and
![]() ${\boldsymbol {h}}_{z}^{\circ }$
corresponding to
${\boldsymbol {h}}_{z}^{\circ }$
corresponding to
![]() ${\boldsymbol {f}}_{x}$
,
${\boldsymbol {f}}_{x}$
,
![]() ${\boldsymbol {g}}_{y}$
and
${\boldsymbol {g}}_{y}$
and
![]() ${\boldsymbol {h}}_{z}$
. We shall say that a point
${\boldsymbol {h}}_{z}$
. We shall say that a point
 $(x,y,z)\in \mathfrak {X}_{\mathcal {R}}^{{\boldsymbol {f}}}$
is crystalline if the conductors of
$(x,y,z)\in \mathfrak {X}_{\mathcal {R}}^{{\boldsymbol {f}}}$
is crystalline if the conductors of
![]() ${\boldsymbol {f}}_{x}^{\circ }$
,
${\boldsymbol {f}}_{x}^{\circ }$
,
![]() ${\boldsymbol {g}}_{y}^{\circ }$
and
${\boldsymbol {g}}_{y}^{\circ }$
and
![]() ${\boldsymbol {h}}_{z}^{\circ }$
are all prime-to-p.
${\boldsymbol {h}}_{z}^{\circ }$
are all prime-to-p.
Theorem 2.1. Assume that
![]() ${\boldsymbol {f}}$
satisfies hypothesis (CR) and that, in addition to hypothesis
${\boldsymbol {f}}$
satisfies hypothesis (CR) and that, in addition to hypothesis
![]() $(\Sigma ^{-}=\emptyset )$
, the triple
$(\Sigma ^{-}=\emptyset )$
, the triple
![]() $({\boldsymbol {f}},{\boldsymbol {g}},{\boldsymbol {h}})$
satisfies
$({\boldsymbol {f}},{\boldsymbol {g}},{\boldsymbol {h}})$
satisfies
-
(ev)
 $\chi _{{\boldsymbol {f}}}\chi _{{\boldsymbol {g}}}\chi _{{\boldsymbol {h}}}=\omega ^{2a}$
for some
$\chi _{{\boldsymbol {f}}}\chi _{{\boldsymbol {g}}}\chi _{{\boldsymbol {h}}}=\omega ^{2a}$
for some
 $a\in \mathbf {Z}$
,
$a\in \mathbf {Z}$
, -
(sq)
 $\mathrm{gcd}(N_{\boldsymbol {f}},N_{\boldsymbol {g}},N_{\boldsymbol {h}})$
is squarefree.
$\mathrm{gcd}(N_{\boldsymbol {f}},N_{\boldsymbol {g}},N_{\boldsymbol {h}})$
is squarefree.
Fix a generator
![]() $\eta _{{\boldsymbol {f}}}$
of the congruence module of
$\eta _{{\boldsymbol {f}}}$
of the congruence module of
![]() ${\boldsymbol {f}}$
. Then there exist
${\boldsymbol {f}}$
. Then there exist
![]() $\Lambda $
-adic test vectors
$\Lambda $
-adic test vectors
 $(\underline {\breve {{\boldsymbol {f}}}},\underline {\breve {{\boldsymbol {g}}}},\underline {\breve {{\boldsymbol {h}}}})$
and an element
$(\underline {\breve {{\boldsymbol {f}}}},\underline {\breve {{\boldsymbol {g}}}},\underline {\breve {{\boldsymbol {h}}}})$
and an element
 $\mathscr {L}_{p}^{f}(\underline {\breve {{\boldsymbol {f}}}},\underline {\breve {{\boldsymbol {g}}}},\underline {\breve {{\boldsymbol {h}}}})\in \mathcal {R}$
such that for all crystalline
$\mathscr {L}_{p}^{f}(\underline {\breve {{\boldsymbol {f}}}},\underline {\breve {{\boldsymbol {g}}}},\underline {\breve {{\boldsymbol {h}}}})\in \mathcal {R}$
such that for all crystalline
 $(x,y,z)\in \mathfrak {X}_{\mathcal {R}}^{\boldsymbol {f}}$
of weight
$(x,y,z)\in \mathfrak {X}_{\mathcal {R}}^{\boldsymbol {f}}$
of weight
![]() $(k,\ell ,m)$
, we have
$(k,\ell ,m)$
, we have
 $$ \begin{align*} \mathscr{L}_{p}^{f}(\underline{\breve{{\boldsymbol{f}}}},\underline{\breve{{\boldsymbol{g}}}},\underline{\breve{{\boldsymbol{h}}}})(x,y,z)^{2}=\Gamma(k,\ell,m)\cdot\mathcal{E}_{p}({\boldsymbol{f}}_{x},{\boldsymbol{g}}_{y},{\boldsymbol{h}}_{z})^{2}\cdot\prod_{q\mid N}\tau_{q}^{2}\cdot\frac{L({\boldsymbol{f}}_{x}^{\circ}\otimes {\boldsymbol{g}}_{y}^{\circ}\otimes {\boldsymbol{h}}_{z}^{\circ},c)}{(\sqrt{-1})^{2k}\cdot\Omega_{{\boldsymbol{f}}_{x}}^{2}}, \end{align*} $$
$$ \begin{align*} \mathscr{L}_{p}^{f}(\underline{\breve{{\boldsymbol{f}}}},\underline{\breve{{\boldsymbol{g}}}},\underline{\breve{{\boldsymbol{h}}}})(x,y,z)^{2}=\Gamma(k,\ell,m)\cdot\mathcal{E}_{p}({\boldsymbol{f}}_{x},{\boldsymbol{g}}_{y},{\boldsymbol{h}}_{z})^{2}\cdot\prod_{q\mid N}\tau_{q}^{2}\cdot\frac{L({\boldsymbol{f}}_{x}^{\circ}\otimes {\boldsymbol{g}}_{y}^{\circ}\otimes {\boldsymbol{h}}_{z}^{\circ},c)}{(\sqrt{-1})^{2k}\cdot\Omega_{{\boldsymbol{f}}_{x}}^{2}}, \end{align*} $$
where
-
•
 $c=(k+\ell +m-2)/2$
,
$c=(k+\ell +m-2)/2$
, -
•
 $\Gamma (k,\ell ,m)=(c-1)!\cdot (c-m)!\cdot (c-\ell )!\cdot (c+1-\ell -m)!\cdot 2^4 (2\pi)^{-2k}$
,
$\Gamma (k,\ell ,m)=(c-1)!\cdot (c-m)!\cdot (c-\ell )!\cdot (c+1-\ell -m)!\cdot 2^4 (2\pi)^{-2k}$
, -
•
 $\mathcal {E}_{p}({\boldsymbol {f}}_{x},{\boldsymbol {g}}_{y},{\boldsymbol {h}}_{z})=(1-\frac {\beta _{{\boldsymbol {f}}_{x}}\alpha _{{\boldsymbol {g}}_{y}}\alpha _{{\boldsymbol {h}}_{z}}}{p^{c}})(1-\frac {\beta _{{\boldsymbol {f}}_{x}}\beta _{{\boldsymbol {g}}_{y}}\alpha _{{\boldsymbol {h}}_{z}}}{p^{c}})(1-\frac {\beta _{{\boldsymbol {f}}_{x}}\alpha _{{\boldsymbol {g}}_{y}}\beta _{{\boldsymbol {h}}_{z}}}{p^{c}})(1-\frac {\beta _{{\boldsymbol {f}}_{x}}\beta _{{\boldsymbol {g}}_{y}}\beta _{{\boldsymbol {h}}_{z}}}{p^{c}})$
,
$\mathcal {E}_{p}({\boldsymbol {f}}_{x},{\boldsymbol {g}}_{y},{\boldsymbol {h}}_{z})=(1-\frac {\beta _{{\boldsymbol {f}}_{x}}\alpha _{{\boldsymbol {g}}_{y}}\alpha _{{\boldsymbol {h}}_{z}}}{p^{c}})(1-\frac {\beta _{{\boldsymbol {f}}_{x}}\beta _{{\boldsymbol {g}}_{y}}\alpha _{{\boldsymbol {h}}_{z}}}{p^{c}})(1-\frac {\beta _{{\boldsymbol {f}}_{x}}\alpha _{{\boldsymbol {g}}_{y}}\beta _{{\boldsymbol {h}}_{z}}}{p^{c}})(1-\frac {\beta _{{\boldsymbol {f}}_{x}}\beta _{{\boldsymbol {g}}_{y}}\beta _{{\boldsymbol {h}}_{z}}}{p^{c}})$
, -
•
 $\tau _{q}$
is a nonzero constant (equal to either
$\tau _{q}$
is a nonzero constant (equal to either
 $1$
or
$1$
or
 $1+q^{-1}$
),
$1+q^{-1}$
), -
•
 $\Omega _{{\boldsymbol {f}}_{x}}\in \mathbf {C}^{\times }$
is the canonical period in [Reference Hsieh28, Def. 3.12] computed with respect to
$\Omega _{{\boldsymbol {f}}_{x}}\in \mathbf {C}^{\times }$
is the canonical period in [Reference Hsieh28, Def. 3.12] computed with respect to
 $\eta _{{\boldsymbol {f}}}$
,
$\eta _{{\boldsymbol {f}}}$
,
and
![]() $L({\boldsymbol {f}}_{x}^{\circ }\otimes {\boldsymbol {g}}_{y}^{\circ }\otimes {\boldsymbol {h}}_{z}^{\circ },c)$
is the central value of the triple product L-function.
$L({\boldsymbol {f}}_{x}^{\circ }\otimes {\boldsymbol {g}}_{y}^{\circ }\otimes {\boldsymbol {h}}_{z}^{\circ },c)$
is the central value of the triple product L-function.
Proof. This is a special case of Theorem A in [Reference Hsieh28]. The construction of
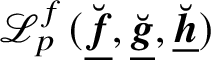 $\mathscr {L}_{p}^{f}(\underline {\breve {{\boldsymbol {f}}}},\underline {\breve {{\boldsymbol {g}}}},\underline {\breve {{\boldsymbol {h}}}})$
under hypotheses (CR), (ev) and (sq) is given in [Reference Hsieh28, §3.6]; the proof of its interpolation property (for all points
$\mathscr {L}_{p}^{f}(\underline {\breve {{\boldsymbol {f}}}},\underline {\breve {{\boldsymbol {g}}}},\underline {\breve {{\boldsymbol {h}}}})$
under hypotheses (CR), (ev) and (sq) is given in [Reference Hsieh28, §3.6]; the proof of its interpolation property (for all points
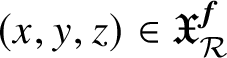 $(x,y,z)\in \mathfrak {X}_{\mathcal {R}}^{\boldsymbol {f}}$
, rather than just those that are crystalline) assuming hypothesis (
$(x,y,z)\in \mathfrak {X}_{\mathcal {R}}^{\boldsymbol {f}}$
, rather than just those that are crystalline) assuming hypothesis (
![]() $\Sigma ^{-}=\emptyset $
) is given in [Reference Hsieh28, §7].
$\Sigma ^{-}=\emptyset $
) is given in [Reference Hsieh28, §7].
Remark 2.2. The construction of
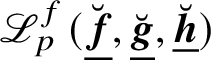 $\mathscr {L}_{p}^{f}(\underline {\breve {{\boldsymbol {f}}}},\underline {\breve {{\boldsymbol {g}}}},\underline {\breve {{\boldsymbol {h}}}})$
is based on Hida’s p-adic Rankin–Selberg convolution [Reference Hida23] and applies to any choice of test vectors for
$\mathscr {L}_{p}^{f}(\underline {\breve {{\boldsymbol {f}}}},\underline {\breve {{\boldsymbol {g}}}},\underline {\breve {{\boldsymbol {h}}}})$
is based on Hida’s p-adic Rankin–Selberg convolution [Reference Hida23] and applies to any choice of test vectors for
![]() $({\boldsymbol {f}},{\boldsymbol {g}},{\boldsymbol {h}})$
. In the following, for any test vectors
$({\boldsymbol {f}},{\boldsymbol {g}},{\boldsymbol {h}})$
. In the following, for any test vectors
![]() $({\breve {{\boldsymbol {f}}}},{\breve {{\boldsymbol {g}}}},{\breve {{\boldsymbol {h}}}})$
we use
$({\breve {{\boldsymbol {f}}}},{\breve {{\boldsymbol {g}}}},{\breve {{\boldsymbol {h}}}})$
we use
 $\mathscr {L}_{p}^{f}({\breve {{\boldsymbol {f}}}},{\breve {{\boldsymbol {g}}}},{\breve {{\boldsymbol {h}}}})$
to denote the associated triple product p-adic L-function (but note that in the proof of our main results the specific choice
$\mathscr {L}_{p}^{f}({\breve {{\boldsymbol {f}}}},{\breve {{\boldsymbol {g}}}},{\breve {{\boldsymbol {h}}}})$
to denote the associated triple product p-adic L-function (but note that in the proof of our main results the specific choice
 $(\underline {\breve {{\boldsymbol {f}}}},\underline {\breve {{\boldsymbol {g}}}},\underline {\breve {{\boldsymbol {h}}}})$
will be critical).
$(\underline {\breve {{\boldsymbol {f}}}},\underline {\breve {{\boldsymbol {g}}}},\underline {\breve {{\boldsymbol {h}}}})$
will be critical).
2.3 Triple tensor product of big Galois representations
Let
![]() $({\boldsymbol {f}},{\boldsymbol {g}},{\boldsymbol {h}})$
be a triple of primitive Hida families with
$({\boldsymbol {f}},{\boldsymbol {g}},{\boldsymbol {h}})$
be a triple of primitive Hida families with
 $\chi _{{\boldsymbol {f}}}\chi _{{\boldsymbol {g}}}\chi _{{\boldsymbol {h}}}=\omega ^{2a}$
for some
$\chi _{{\boldsymbol {f}}}\chi _{{\boldsymbol {g}}}\chi _{{\boldsymbol {h}}}=\omega ^{2a}$
for some
![]() $a\in \mathbf {Z}$
. For
$a\in \mathbf {Z}$
. For
![]() $\boldsymbol {\phi }\in \{{\boldsymbol {f}},{\boldsymbol {g}},{\boldsymbol {h}}\}$
, let
$\boldsymbol {\phi }\in \{{\boldsymbol {f}},{\boldsymbol {g}},{\boldsymbol {h}}\}$
, let
![]() $V_{\boldsymbol {\phi }}$
be the natural lattice in
$V_{\boldsymbol {\phi }}$
be the natural lattice in
![]() $(\text {Frac}\;\mathbb {I}_{\boldsymbol {\phi }})^{2}$
realising the Galois representation
$(\text {Frac}\;\mathbb {I}_{\boldsymbol {\phi }})^{2}$
realising the Galois representation
![]() $\rho _{\boldsymbol {\phi }}$
in the étale cohomology of modular curves (see [Reference Ohta34]) and set
$\rho _{\boldsymbol {\phi }}$
in the étale cohomology of modular curves (see [Reference Ohta34]) and set
This has rank
![]() $8$
over
$8$
over
![]() $\mathcal {R}$
, and by hypothesis its determinant can be written as
$\mathcal {R}$
, and by hypothesis its determinant can be written as
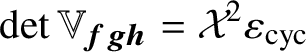 $\det \mathbb {V}_{{\boldsymbol {f}}{\boldsymbol {g}}{\boldsymbol {h}}}=\mathcal {X}^{2}\varepsilon _{\text {cyc}}$
for a p-ramified Galois character
$\det \mathbb {V}_{{\boldsymbol {f}}{\boldsymbol {g}}{\boldsymbol {h}}}=\mathcal {X}^{2}\varepsilon _{\text {cyc}}$
for a p-ramified Galois character
![]() $\mathcal {X}$
taking the value
$\mathcal {X}$
taking the value
![]() $(-1)^{a}$
at complex conjugation. Similar to [Reference Howard27, Def. 2.1.3], we define the critical twist
$(-1)^{a}$
at complex conjugation. Similar to [Reference Howard27, Def. 2.1.3], we define the critical twist
 $$ \begin{align*} \mathbb{V}_{{\boldsymbol{f}}{\boldsymbol{g}}{\boldsymbol{h}}}^{\dagger}:=\mathbb{V}_{{\boldsymbol{f}}{\boldsymbol{g}}{\boldsymbol{h}}}\otimes\mathcal{X}^{-1}.\nonumber \end{align*} $$
$$ \begin{align*} \mathbb{V}_{{\boldsymbol{f}}{\boldsymbol{g}}{\boldsymbol{h}}}^{\dagger}:=\mathbb{V}_{{\boldsymbol{f}}{\boldsymbol{g}}{\boldsymbol{h}}}\otimes\mathcal{X}^{-1}.\nonumber \end{align*} $$
More generally, for any multiple N of
![]() $N_{\boldsymbol {\phi }}$
, one can define Galois modules
$N_{\boldsymbol {\phi }}$
, one can define Galois modules
![]() $V_{\boldsymbol {\phi }}(N)$
by working in tame level N; these split noncanonically into a finite direct sum of the
$V_{\boldsymbol {\phi }}(N)$
by working in tame level N; these split noncanonically into a finite direct sum of the
![]() $\mathbb {I}_{\boldsymbol {\phi }}$
-adic representations
$\mathbb {I}_{\boldsymbol {\phi }}$
-adic representations
![]() $V_{\boldsymbol {\phi }}$
(see [Reference Darmon and Rotger18, §1.5.3]), and they define
$V_{\boldsymbol {\phi }}$
(see [Reference Darmon and Rotger18, §1.5.3]), and they define
 $\mathbb {V}_{{\boldsymbol {f}}{\boldsymbol {g}}{\boldsymbol {h}}}^{\dagger }(N)$
for any N divisible by
$\mathbb {V}_{{\boldsymbol {f}}{\boldsymbol {g}}{\boldsymbol {h}}}^{\dagger }(N)$
for any N divisible by
![]() $\text {lcm}(N_{{\boldsymbol {f}}},N_{{\boldsymbol {g}}},N_{{\boldsymbol {h}}})$
.
$\text {lcm}(N_{{\boldsymbol {f}}},N_{{\boldsymbol {g}}},N_{{\boldsymbol {h}}})$
.
If f is a classical specialisation of
![]() ${\boldsymbol {f}}$
with associated p-adic Galois representation
${\boldsymbol {f}}$
with associated p-adic Galois representation
![]() $V_{f}$
, we let
$V_{f}$
, we let
![]() $\mathbb {V}_{f,{\boldsymbol {g}}{\boldsymbol {h}}}$
be the quotient of
$\mathbb {V}_{f,{\boldsymbol {g}}{\boldsymbol {h}}}$
be the quotient of
![]() $\mathbb {V}_{{\boldsymbol {f}}{\boldsymbol {g}}{\boldsymbol {h}}}$
given by
$\mathbb {V}_{{\boldsymbol {f}}{\boldsymbol {g}}{\boldsymbol {h}}}$
given by
and denote by
 $\mathbb {V}^{\dagger }_{f,{{\boldsymbol {g}}{\boldsymbol {h}}}}$
the corresponding quotient of
$\mathbb {V}^{\dagger }_{f,{{\boldsymbol {g}}{\boldsymbol {h}}}}$
the corresponding quotient of
 $\mathbb {V}^{\dagger }_{{\boldsymbol {f}}{\boldsymbol {g}}{\boldsymbol {h}}}$
and by
$\mathbb {V}^{\dagger }_{{\boldsymbol {f}}{\boldsymbol {g}}{\boldsymbol {h}}}$
and by
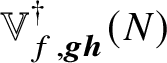 $\mathbb {V}^{\dagger }_{f,{{\boldsymbol {g}}{\boldsymbol {h}}}}(N)$
its level N counterpart.
$\mathbb {V}^{\dagger }_{f,{{\boldsymbol {g}}{\boldsymbol {h}}}}(N)$
its level N counterpart.
2.4 Theta elements and factorisation
We recall the factorisation proven in [Reference Hsieh28, §8]. Let
![]() $f\in S_{2}(pN_{f})$
be a p-stabilised newform of tame level
$f\in S_{2}(pN_{f})$
be a p-stabilised newform of tame level
![]() $N_{f}$
defined over
$N_{f}$
defined over
![]() $\mathcal O$
, let
$\mathcal O$
, let
![]() $f^{\circ }\in S_{2}(N_{f})$
be the associated newform and let
$f^{\circ }\in S_{2}(N_{f})$
be the associated newform and let
![]() $\alpha _{p}=\alpha _{p}(f)\in \mathcal O^{\times }$
be the
$\alpha _{p}=\alpha _{p}(f)\in \mathcal O^{\times }$
be the
![]() $U_{p}$
-eigenvalue of f. Let K be an imaginary quadratic field of discriminant
$U_{p}$
-eigenvalue of f. Let K be an imaginary quadratic field of discriminant
![]() $D_{K}$
prime to
$D_{K}$
prime to
![]() $N_{f}$
. Write
$N_{f}$
. Write
with
![]() $N^{+}$
(respectively
$N^{+}$
(respectively
![]() $N^{-}$
) divisible only by primes which are split (respectively inert) in K and choose an ideal
$N^{-}$
) divisible only by primes which are split (respectively inert) in K and choose an ideal
![]() $\mathfrak {N}^{+}\subset \mathcal O_{K}$
with
$\mathfrak {N}^{+}\subset \mathcal O_{K}$
with
![]() $\mathcal O_{K}/\mathfrak {N}^{+}\simeq \mathbf {Z}/N^{+}\mathbf {Z}$
.
$\mathcal O_{K}/\mathfrak {N}^{+}\simeq \mathbf {Z}/N^{+}\mathbf {Z}$
.
Assume that
![]() $(p)=\mathfrak {p}\overline {\mathfrak {p}}$
splits in K, with our fixed embedding
$(p)=\mathfrak {p}\overline {\mathfrak {p}}$
splits in K, with our fixed embedding
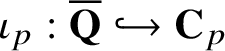 $\iota _{p}:\overline {\mathbf {Q}}\hookrightarrow \mathbf {C}_{p}$
inducing the prime
$\iota _{p}:\overline {\mathbf {Q}}\hookrightarrow \mathbf {C}_{p}$
inducing the prime
![]() $\mathfrak {p}$
. Let
$\mathfrak {p}$
. Let
![]() $\Gamma _{\infty }$
be the Galois group of the anticyclotomic
$\Gamma _{\infty }$
be the Galois group of the anticyclotomic
![]() $\mathbf {Z}_{p}$
-extension
$\mathbf {Z}_{p}$
-extension
![]() $K_{\infty }/K$
and fix a topological generator
$K_{\infty }/K$
and fix a topological generator
![]() ${\boldsymbol \gamma }\in \Gamma _{\infty }$
and identity
${\boldsymbol \gamma }\in \Gamma _{\infty }$
and identity
![]() with the power series ring
with the power series ring
![]() via
via
![]() ${\boldsymbol \gamma }\mapsto 1+T$
. For any prime-to-p ideal
${\boldsymbol \gamma }\mapsto 1+T$
. For any prime-to-p ideal
![]() $\mathfrak a$
of K, let
$\mathfrak a$
of K, let
![]() $\sigma _{\mathfrak a}$
be the image of
$\sigma _{\mathfrak a}$
be the image of
![]() $\mathfrak a$
in the Galois group of the ray class field
$\mathfrak a$
in the Galois group of the ray class field
![]() $K(p^{\infty })/K$
of conductor
$K(p^{\infty })/K$
of conductor
![]() $p^{\infty }$
under the geometrically normalised reciprocity law map.
$p^{\infty }$
under the geometrically normalised reciprocity law map.
Theorem 2.3. Let
![]() $\chi $
be a ring class character of K of conductor
$\chi $
be a ring class character of K of conductor
![]() $c\mathcal O_{K}$
with values in
$c\mathcal O_{K}$
with values in
![]() $\mathcal O$
and assume that
$\mathcal O$
and assume that
-
(i)
 $(pN_{f},cD_{K})=1$
,
$(pN_{f},cD_{K})=1$
, -
(ii)
 $N^{-}$
is the squarefree product of an odd number of primes,
$N^{-}$
is the squarefree product of an odd number of primes, -
(iii) if
 $q\vert N^{-}$
is a prime with
$q\vert N^{-}$
is a prime with
 $q\equiv 1\pmod {p}$
, then
$q\equiv 1\pmod {p}$
, then
 $\bar {\rho }_{f}$
is ramified at q.
$\bar {\rho }_{f}$
is ramified at q.
Then there exists a unique
![]() such that for every p-power root of unity
such that for every p-power root of unity
![]() $\zeta $
,
$\zeta $
,
 $$ \begin{align*} \Theta^{}_{f/K,\chi}(\zeta-1)^{2}=\frac{p^{n}}{\alpha_{p}^{2n}}\cdot\mathcal{E}_{p}(f,\chi,\zeta)^{2}\cdot\frac{L(f^{\circ}/K\otimes\chi\epsilon_{\zeta},1)}{(2\pi)^{2}\cdot \Omega_{f^{\circ},N^{-}}}\cdot u_{K}^{2}\sqrt{D_{K}}\chi\epsilon_{\zeta}(\sigma_{\mathfrak{N}^{+}})\cdot\varepsilon_{p},\\[-15pt] \end{align*} $$
$$ \begin{align*} \Theta^{}_{f/K,\chi}(\zeta-1)^{2}=\frac{p^{n}}{\alpha_{p}^{2n}}\cdot\mathcal{E}_{p}(f,\chi,\zeta)^{2}\cdot\frac{L(f^{\circ}/K\otimes\chi\epsilon_{\zeta},1)}{(2\pi)^{2}\cdot \Omega_{f^{\circ},N^{-}}}\cdot u_{K}^{2}\sqrt{D_{K}}\chi\epsilon_{\zeta}(\sigma_{\mathfrak{N}^{+}})\cdot\varepsilon_{p},\\[-15pt] \end{align*} $$
where
-
•
 $n\geqslant 0$
is such that
$n\geqslant 0$
is such that
 $\zeta $
has exact order
$\zeta $
has exact order
 $p^{n}$
,
$p^{n}$
, -
•
 $\epsilon _{\zeta }:\Gamma _{\infty }\rightarrow \mu _{p^{\infty }}$
be the character defined by
$\epsilon _{\zeta }:\Gamma _{\infty }\rightarrow \mu _{p^{\infty }}$
be the character defined by
 $\epsilon _{\zeta }({\boldsymbol \gamma })=\zeta $
,
$\epsilon _{\zeta }({\boldsymbol \gamma })=\zeta $
, -
•
 $\mathcal {E}_{p}(f,\chi ,\zeta )= \begin {cases} (1-\alpha _{p}^{-1}\chi (\mathfrak {p}))(1-\alpha _{p}\chi (\overline {\mathfrak {p}}))& \mbox {if }n=0\textrm {,}\\ 1&\mbox {if }n>0\textrm {,} \end {cases}$
$\mathcal {E}_{p}(f,\chi ,\zeta )= \begin {cases} (1-\alpha _{p}^{-1}\chi (\mathfrak {p}))(1-\alpha _{p}\chi (\overline {\mathfrak {p}}))& \mbox {if }n=0\textrm {,}\\ 1&\mbox {if }n>0\textrm {,} \end {cases}$
-
•
 $\Omega _{f^{\circ },N^{-}}=4\Vert f^{\circ }\Vert _{\Gamma _{0}(N_{f})}^{2}\cdot \eta _{f,N^{-}}^{-1}$
is the Gross period of
$\Omega _{f^{\circ },N^{-}}=4\Vert f^{\circ }\Vert _{\Gamma _{0}(N_{f})}^{2}\cdot \eta _{f,N^{-}}^{-1}$
is the Gross period of
 $f^{\circ }$
(see [Reference Hsieh28, p. 524]),
$f^{\circ }$
(see [Reference Hsieh28, p. 524]), -
•
 $\sigma _{\mathfrak {N}^{+}}\in \Gamma _{\infty }$
is the image of
$\sigma _{\mathfrak {N}^{+}}\in \Gamma _{\infty }$
is the image of
 $\mathfrak {N}^{+}$
under the geometrically normalised Artin’s reciprocity map,
$\mathfrak {N}^{+}$
under the geometrically normalised Artin’s reciprocity map, -
•
 $u_{K}=\vert \mathcal O_{K}^{\times }\vert /2$
and
$u_{K}=\vert \mathcal O_{K}^{\times }\vert /2$
and
 $\varepsilon _{p}\in \{\pm 1\}$
is the local root number of
$\varepsilon _{p}\in \{\pm 1\}$
is the local root number of
 $f^{\circ }$
at p.
$f^{\circ }$
at p.
Proof. See [Reference Bertolini and Darmon4] for the first construction and [Reference Chida and Hsieh13, Thm. A] for the stated interpolation property.
Remark 2.4. From the interpolation property of Theorem 2.3, one can show that the square of
![]() $\Theta _{f/K,\chi }(T)$
is essentially the anticyclomic restriction of the two-variable p-adic L-function constructed by Perrin-Riou [Reference Perrin-Riou35].
$\Theta _{f/K,\chi }(T)$
is essentially the anticyclomic restriction of the two-variable p-adic L-function constructed by Perrin-Riou [Reference Perrin-Riou35].
When
![]() $\chi $
is the trivial character, we write
$\chi $
is the trivial character, we write
![]() $\Theta _{f/K,\chi }(T)$
simply as
$\Theta _{f/K,\chi }(T)$
simply as
![]() $\Theta _{f/K}(T)$
. Suppose now that the p-stabilised newform f as in Theorem 2.3 is the specialisation of a primitive Hida family
$\Theta _{f/K}(T)$
. Suppose now that the p-stabilised newform f as in Theorem 2.3 is the specialisation of a primitive Hida family
![]() ${\boldsymbol {f}}\in S^{o}(N_{f},\mathbb {I})$
with branch character
${\boldsymbol {f}}\in S^{o}(N_{f},\mathbb {I})$
with branch character
at an arithmetic point
![]() $x_{1}\in \mathfrak {X}_{\mathbb {I}}^{+}$
of weight
$x_{1}\in \mathfrak {X}_{\mathbb {I}}^{+}$
of weight
![]() $2$
. Let
$2$
. Let
![]() $\ell \nmid pN_{f}$
be a prime split in K and let
$\ell \nmid pN_{f}$
be a prime split in K and let
![]() $\chi $
be a ring class character of K of conductor
$\chi $
be a ring class character of K of conductor
![]() $\ell ^{m}\mathcal O_{K}$
for some
$\ell ^{m}\mathcal O_{K}$
for some
![]() $m>0$
. Denoting by the superscript
$m>0$
. Denoting by the superscript
![]() $\tau $
the action of the nontrivial automorphism of
$\tau $
the action of the nontrivial automorphism of
![]() $K/\mathbf {Q}$
, write
$K/\mathbf {Q}$
, write
![]() $\chi =\psi ^{1-\tau }$
with
$\chi =\psi ^{1-\tau }$
with
![]() $\psi $
a ray class character modulo
$\psi $
a ray class character modulo
![]() $\ell ^{m}\mathcal O_{K}$
. Set
$\ell ^{m}\mathcal O_{K}$
. Set
![]() $C=D_{K}\ell ^{2m}$
and let
$C=D_{K}\ell ^{2m}$
and let
be the primitive CM Hida families of level C constructed in [Reference Hsieh28, §8.3].
The p-adic L-function
 $\mathscr {L}_{p}^{f}(\underline {\breve {{\boldsymbol {f}}}},\underline {\breve {{\boldsymbol {g}}}},\underline {\breve {{\boldsymbol {g}}}}^{*})$
of Theorem 2.1 attached to the triple
$\mathscr {L}_{p}^{f}(\underline {\breve {{\boldsymbol {f}}}},\underline {\breve {{\boldsymbol {g}}}},\underline {\breve {{\boldsymbol {g}}}}^{*})$
of Theorem 2.1 attached to the triple
![]() $({\boldsymbol {f}},{\boldsymbol {g}},{\boldsymbol {g}}^{*})$
(taking
$({\boldsymbol {f}},{\boldsymbol {g}},{\boldsymbol {g}}^{*})$
(taking
![]() $a=-1$
in (ev)) is an element in
$a=-1$
in (ev)) is an element in
; in the following, we let
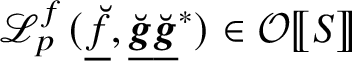
denote the restriction to the ‘line’
![]() $S=S_{2}=S_{3}$
of the image of
$S=S_{2}=S_{3}$
of the image of
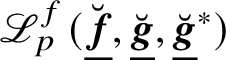 $\mathscr {L}_{p}^{f}(\underline {\breve {{\boldsymbol {f}}}},\underline {\breve {{\boldsymbol {g}}}},\underline {\breve {{\boldsymbol {g}}}}^{*})$
under the specialisation map at
$\mathscr {L}_{p}^{f}(\underline {\breve {{\boldsymbol {f}}}},\underline {\breve {{\boldsymbol {g}}}},\underline {\breve {{\boldsymbol {g}}}}^{*})$
under the specialisation map at
![]() $x_{1}$
.
$x_{1}$
.
Let
![]() $\mathbb {K}_{\infty }$
be the
$\mathbb {K}_{\infty }$
be the
![]() $\mathbf {Z}_{p}^{2}$
-extension of K and let
$\mathbf {Z}_{p}^{2}$
-extension of K and let
![]() $K_{\mathfrak {p}^{\infty }}$
denote the
$K_{\mathfrak {p}^{\infty }}$
denote the
![]() $\mathfrak {p}$
-ramified
$\mathfrak {p}$
-ramified
![]() $\mathbf {Z}_{p}$
-extension in
$\mathbf {Z}_{p}$
-extension in
![]() $\mathbb {K}_{\infty }$
, with Galois group
$\mathbb {K}_{\infty }$
, with Galois group
![]() $\Gamma _{\mathfrak {p}^{\infty }}=\text {Gal}(K_{\mathfrak {p}^{\infty }}/K)$
. Let
$\Gamma _{\mathfrak {p}^{\infty }}=\text {Gal}(K_{\mathfrak {p}^{\infty }}/K)$
. Let
![]() $\gamma _{\mathfrak {p}}\in \Gamma _{\mathfrak {p}^{\infty }}$
be a topological generator and for the formal variable T let
$\gamma _{\mathfrak {p}}\in \Gamma _{\mathfrak {p}^{\infty }}$
be a topological generator and for the formal variable T let
![]() be the universal character defined by
be the universal character defined by
 $$ \begin{align} \Psi_{T}(\sigma)=(1+T)^{l(\sigma)},\quad\mbox{where }\sigma\vert_{K_{\mathfrak{p}^{\infty}}}=\gamma_{\mathfrak{p}}^{l(\sigma)}.\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} \Psi_{T}(\sigma)=(1+T)^{l(\sigma)},\quad\mbox{where }\sigma\vert_{K_{\mathfrak{p}^{\infty}}}=\gamma_{\mathfrak{p}}^{l(\sigma)}.\\[-15pt]\nonumber \end{align} $$
The character
 $\Psi _{T}^{1-\tau }$
factors through
$\Psi _{T}^{1-\tau }$
factors through
![]() $\Gamma _{\infty }$
and yields an identification
$\Gamma _{\infty }$
and yields an identification
![]() corresponding to the topological generator
corresponding to the topological generator
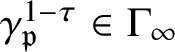 $\gamma _{\mathfrak {p}}^{1-\tau }\in \Gamma _{\infty }$
. Let
$\gamma _{\mathfrak {p}}^{1-\tau }\in \Gamma _{\infty }$
. Let
![]() $p^{b}$
be the order of the p-part of the class number of K. Hereafter, we shall fix
$p^{b}$
be the order of the p-part of the class number of K. Hereafter, we shall fix
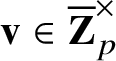 $\mathbf v\in \overline {\mathbf {Z}}_{p}^{\times }$
such that
$\mathbf v\in \overline {\mathbf {Z}}_{p}^{\times }$
such that
 $\mathbf v^{p^{b}}=\varepsilon _{\text {cyc}}(\gamma _{\mathfrak p}^{p^{b}})\in 1+p\mathbf {Z}_{p}$
. Let
$\mathbf v^{p^{b}}=\varepsilon _{\text {cyc}}(\gamma _{\mathfrak p}^{p^{b}})\in 1+p\mathbf {Z}_{p}$
. Let
![]() $K(\chi ,\alpha _{p})/K$
(respectively
$K(\chi ,\alpha _{p})/K$
(respectively
![]() $K(\chi )/K$
) be the finite extension obtained by adjoining to K the values of
$K(\chi )/K$
) be the finite extension obtained by adjoining to K the values of
![]() $\chi $
and
$\chi $
and
![]() $\alpha _{p}$
(respectively the values of
$\alpha _{p}$
(respectively the values of
![]() $\chi $
).
$\chi $
).
Proposition 2.5. Assume that
-
(i)
 $N^{-}$
is the squarefree product of an odd number of primes,
$N^{-}$
is the squarefree product of an odd number of primes, -
(ii)
 $\bar {\rho }_{f}$
is ramified at every prime
$\bar {\rho }_{f}$
is ramified at every prime
 $q\vert N^{-}$
with
$q\vert N^{-}$
with
 $q\equiv 1\pmod {p}$
.
$q\equiv 1\pmod {p}$
.
Set
![]() $T=\mathbf {v}^{-1}(1+S)-1$
. Then
$T=\mathbf {v}^{-1}(1+S)-1$
. Then
 $$ \begin{align*} \mathscr{L}_{p}^{f}(\underline{\breve{f}},\underline{\breve{{\boldsymbol{g}}}}\underline{\breve{{\boldsymbol{g}}}}^{*})= \pm\mathbf{w}^{-1}\cdot\Theta_{f/K}(T)\cdot C_{f,\chi}\cdot \sqrt{L^{\mathrm{alg}}(f/K\otimes\chi,1)}\cdot\frac{\eta_{f^{\circ}}}{\eta_{f^{\circ},N^{-}}}, \end{align*} $$
$$ \begin{align*} \mathscr{L}_{p}^{f}(\underline{\breve{f}},\underline{\breve{{\boldsymbol{g}}}}\underline{\breve{{\boldsymbol{g}}}}^{*})= \pm\mathbf{w}^{-1}\cdot\Theta_{f/K}(T)\cdot C_{f,\chi}\cdot \sqrt{L^{\mathrm{alg}}(f/K\otimes\chi,1)}\cdot\frac{\eta_{f^{\circ}}}{\eta_{f^{\circ},N^{-}}}, \end{align*} $$
where
![]() $\mathbf {w}$
is a unit in
$\mathbf {w}$
is a unit in
![]() ,
,
![]() $C_{f,\chi }\in K(\chi ,\alpha _{p})^{\times }$
and
$C_{f,\chi }\in K(\chi ,\alpha _{p})^{\times }$
and
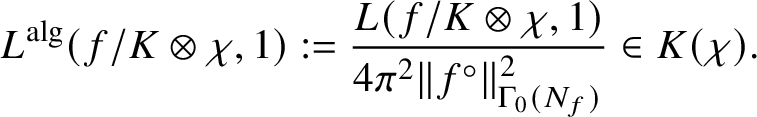 $$ \begin{align*} L^{\mathrm{alg}}(f/K\otimes\chi,1):=\frac{L(f/K\otimes\chi,1)}{4\pi^{2}\lVert f^{\circ}\rVert_{\Gamma_{0}(N_{f})}^{2}}\in K(\chi). \end{align*} $$
$$ \begin{align*} L^{\mathrm{alg}}(f/K\otimes\chi,1):=\frac{L(f/K\otimes\chi,1)}{4\pi^{2}\lVert f^{\circ}\rVert_{\Gamma_{0}(N_{f})}^{2}}\in K(\chi). \end{align*} $$
Proof. This is [Reference Hsieh28, Prop. 8.1] specialised to
![]() $S=S_{2}=S_{3}$
, using the interpolation property of
$S=S_{2}=S_{3}$
, using the interpolation property of
![]() $\Theta _{f/K,\chi }(T)$
at
$\Theta _{f/K,\chi }(T)$
at
![]() $\zeta =1$
. (Note that the unit
$\zeta =1$
. (Note that the unit
![]() $\mathbf {w}$
is explicitly described in [Reference Hsieh28, Prop. 8.1], but we omit it here.)
$\mathbf {w}$
is explicitly described in [Reference Hsieh28, Prop. 8.1], but we omit it here.)
Remark 2.6. The factorisation of Proposition 2.5 reflects the decomposition of Galois representations
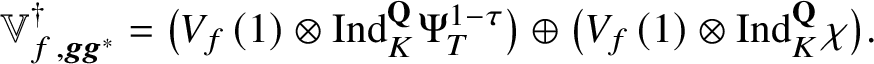 $$ \begin{align} \mathbb{V}_{f,{\boldsymbol{g}}{\boldsymbol{g}}^{*}}^{\dagger}=\big(V_{f}(1)\otimes\textrm{Ind}_{K}^{\mathbf{Q}}\Psi_{T}^{1-\tau}\big)\oplus \big(V_{f}(1)\otimes\textrm{Ind}_{K}^{\mathbf{Q}}\chi\big). \end{align} $$
$$ \begin{align} \mathbb{V}_{f,{\boldsymbol{g}}{\boldsymbol{g}}^{*}}^{\dagger}=\big(V_{f}(1)\otimes\textrm{Ind}_{K}^{\mathbf{Q}}\Psi_{T}^{1-\tau}\big)\oplus \big(V_{f}(1)\otimes\textrm{Ind}_{K}^{\mathbf{Q}}\chi\big). \end{align} $$
Note that the first summand in (2.4) is the anticyclotomic deformation of
![]() $V_{f}(1)$
, while the second is a fixed character twist of
$V_{f}(1)$
, while the second is a fixed character twist of
![]() $V_{f}(1)$
.
$V_{f}(1)$
.
3 Coleman map for relative Lubin–Tate groups
In this section we review Perrin-Riou’s theory [Reference Perrin-Riou36] of big exponential maps, as extended by Kobayashi [Reference Kobayashi30] to
![]() $\mathbf {Z}_{p}$
-extensions arising from torsion points on relative Lubin–Tate formal groups of height 1. Applied to the localisation of the anticyclotomic
$\mathbf {Z}_{p}$
-extensions arising from torsion points on relative Lubin–Tate formal groups of height 1. Applied to the localisation of the anticyclotomic
![]() $\mathbf {Z}_{p}$
-extension of an imaginary quadratic field K in which p splits, we then deduce, by the results of Section 2 and [Reference Darmon and Rotger18], a Coleman power series construction of the p-adic L-function
$\mathbf {Z}_{p}$
-extension of an imaginary quadratic field K in which p splits, we then deduce, by the results of Section 2 and [Reference Darmon and Rotger18], a Coleman power series construction of the p-adic L-function
![]() $\Theta _{f/K}$
of Theorem 2.3. This new construction of
$\Theta _{f/K}$
of Theorem 2.3. This new construction of
![]() $\Theta _{f/K}$
will play an important role in the proof of our main results.
$\Theta _{f/K}$
will play an important role in the proof of our main results.
3.1 Preliminaries
Fix a complete algebraic closure
![]() $\mathbf {C}_{p}$
of
$\mathbf {C}_{p}$
of
![]() ${\mathbf {Q}}_{p}$
. Let
${\mathbf {Q}}_{p}$
. Let
![]() ${\mathbf {Q}}_{p}^{\text {ur}}\subset \mathbf {C}_{p}$
be the maximal unramified extension of
${\mathbf {Q}}_{p}^{\text {ur}}\subset \mathbf {C}_{p}$
be the maximal unramified extension of
![]() ${\mathbf {Q}}_{p}$
and let
${\mathbf {Q}}_{p}$
and let
![]() $\mathrm {Fr}\in \operatorname {\mathrm {Gal}}({\mathbf {Q}}_{p}^{\text {ur}}/{\mathbf {Q}}_{p})$
be the absolute Frobenius. Let
$\mathrm {Fr}\in \operatorname {\mathrm {Gal}}({\mathbf {Q}}_{p}^{\text {ur}}/{\mathbf {Q}}_{p})$
be the absolute Frobenius. Let
![]() $F\subset {\mathbf {Q}}_{p}^{\text {ur}}$
be a finite unramified extension of
$F\subset {\mathbf {Q}}_{p}^{\text {ur}}$
be a finite unramified extension of
![]() ${\mathbf {Q}}_{p}$
with valuation ring
${\mathbf {Q}}_{p}$
with valuation ring
![]() $\mathscr {O}$
and set
$\mathscr {O}$
and set
Let
![]() ${\mathcal F}=\operatorname {\mathrm {Spf}} R$
be a relative Lubin–Tate formal group of height 1 defined over
${\mathcal F}=\operatorname {\mathrm {Spf}} R$
be a relative Lubin–Tate formal group of height 1 defined over
![]() $\mathscr O$
, and for each
$\mathscr O$
, and for each
![]() $n\in \mathbf {Z}$
set
$n\in \mathbf {Z}$
set
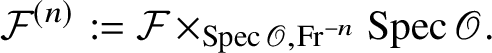 $$ \begin{align*} {\mathcal F}^{(n)}:={\mathcal F}\times_{\mathrm{Spec}\,\mathscr O,\mathrm{Fr}^{-n}}\mathrm{Spec}\,\mathscr O. \end{align*} $$
$$ \begin{align*} {\mathcal F}^{(n)}:={\mathcal F}\times_{\mathrm{Spec}\,\mathscr O,\mathrm{Fr}^{-n}}\mathrm{Spec}\,\mathscr O. \end{align*} $$
The Frobenius morphism
![]() $\varphi _{\mathcal F}\in \operatorname {\mathrm {Hom}}({\mathcal F},{\mathcal F}^{(-1)})$
induces a homomorphism
$\varphi _{\mathcal F}\in \operatorname {\mathrm {Hom}}({\mathcal F},{\mathcal F}^{(-1)})$
induces a homomorphism
![]() $\varphi _{\mathcal F}\colon R\to R$
defined by
$\varphi _{\mathcal F}\colon R\to R$
defined by
where
![]() $f^{\mathrm {Fr}}$
is the conjugate of f by
$f^{\mathrm {Fr}}$
is the conjugate of f by
![]() $\mathrm {Fr}$
. Let
$\mathrm {Fr}$
. Let
![]() $\psi _{\mathcal F}$
be the left inverse of
$\psi _{\mathcal F}$
be the left inverse of
![]() $\varphi _{\mathcal F}$
satisfying
$\varphi _{\mathcal F}$
satisfying
 $$ \begin{align} \varphi_{\mathcal F}\circ\psi_{\mathcal F} (f)=p^{-1}\sum_{x\in {\mathcal F}[p]}f(X\oplus_{\mathcal F} x). \end{align} $$
$$ \begin{align} \varphi_{\mathcal F}\circ\psi_{\mathcal F} (f)=p^{-1}\sum_{x\in {\mathcal F}[p]}f(X\oplus_{\mathcal F} x). \end{align} $$
Let
![]() $F_{\infty }/F$
be the Lubin–Tate
$F_{\infty }/F$
be the Lubin–Tate
![]() $\mathbf {Z}_{p}^{\times }$
-extension of F associated with
$\mathbf {Z}_{p}^{\times }$
-extension of F associated with
![]() ${\mathcal F}$
– that is,
${\mathcal F}$
– that is,
![]() $F_{\infty }=\bigcup _{n=1}^{\infty } F({\mathcal F}[p^{n}])$
– and for every
$F_{\infty }=\bigcup _{n=1}^{\infty } F({\mathcal F}[p^{n}])$
– and for every
![]() $n\geqslant -1$
let
$n\geqslant -1$
let
![]() $F_{n}$
be the subfield of
$F_{n}$
be the subfield of
![]() $F_{\infty }$
with
$F_{\infty }$
with
![]() $\operatorname {\mathrm {Gal}}(F_{n}/F)\simeq (\mathbf {Z}/p^{n+1}\mathbf {Z})^{\times }$
. (Hence,
$\operatorname {\mathrm {Gal}}(F_{n}/F)\simeq (\mathbf {Z}/p^{n+1}\mathbf {Z})^{\times }$
. (Hence,
![]() $F_{-1}=F$
.) Letting
$F_{-1}=F$
.) Letting
![]() $G_{\infty }=\operatorname {\mathrm {Gal}}(F_{\infty }/F)$
, there is a canonical decomposition
$G_{\infty }=\operatorname {\mathrm {Gal}}(F_{\infty }/F)$
, there is a canonical decomposition
with
![]() $\Delta $
the torsion subgroup of
$\Delta $
the torsion subgroup of
![]() $G_{\infty }$
and
$G_{\infty }$
and
![]() $\Gamma ^{\mathcal F}_{\infty }\simeq \mathbf {Z}_{p}$
the maximal torsion-free quotient of
$\Gamma ^{\mathcal F}_{\infty }\simeq \mathbf {Z}_{p}$
the maximal torsion-free quotient of
![]() $G_{\infty }$
.
$G_{\infty }$
.
For every
![]() $a\in \mathbf {Z}_{p}^{\times }$
, there is a unique formal power series
$a\in \mathbf {Z}_{p}^{\times }$
, there is a unique formal power series
![]() $[a]\in R$
such that
$[a]\in R$
such that
Letting
 $\varepsilon _{\mathcal F}\colon G_{\infty }\stackrel {\sim }{\to }\mathbf {Z}_{p}^{\times }$
be the Lubin–Tate character, we let
$\varepsilon _{\mathcal F}\colon G_{\infty }\stackrel {\sim }{\to }\mathbf {Z}_{p}^{\times }$
be the Lubin–Tate character, we let
![]() $\sigma \in G_{\infty }$
act on
$\sigma \in G_{\infty }$
act on
![]() $f\in R$
by
$f\in R$
by
thus making R into an
![]() -module.
-module.
Lemma 3.1.
![]() $R^{\psi _{\mathcal F}=0}$
is free of rank 1 over
$R^{\psi _{\mathcal F}=0}$
is free of rank 1 over
![]() .
.
Proof. This is [Reference Kobayashi30, Prop. 5.4].
Let V be a crystalline
![]() $G_{{\mathbf {Q}}_{p}}$
-representation defined over a finite extension L of
$G_{{\mathbf {Q}}_{p}}$
-representation defined over a finite extension L of
![]() ${\mathbf {Q}}_{p}$
with ring of integers
${\mathbf {Q}}_{p}$
with ring of integers
![]() $\mathcal O_{L}$
. Let
$\mathcal O_{L}$
. Let
![]() ${\mathbf D}(V)={\mathbf D}_{\text {cris},{\mathbf {Q}}_{p}}(V)$
be the filtered
${\mathbf D}(V)={\mathbf D}_{\text {cris},{\mathbf {Q}}_{p}}(V)$
be the filtered
![]() $\varphi $
-module associated with V and set
$\varphi $
-module associated with V and set
 $$ \begin{align*}{\mathscr D}_{\infty}(V):={\mathbf D}(V)\otimes_{\mathbf{Z}_{p}}R^{\psi_{\mathcal F}=0}.\\[-15pt] \end{align*} $$
$$ \begin{align*}{\mathscr D}_{\infty}(V):={\mathbf D}(V)\otimes_{\mathbf{Z}_{p}}R^{\psi_{\mathcal F}=0}.\\[-15pt] \end{align*} $$
Fix an invariant differential
![]() $\omega _{\mathcal F}\in \Omega _{R}$
and let
$\omega _{\mathcal F}\in \Omega _{R}$
and let
![]() $\log _{\mathcal F}\in R\widehat \otimes {\mathbf {Q}}_{p}$
be the logarithm map satisfying
$\log _{\mathcal F}\in R\widehat \otimes {\mathbf {Q}}_{p}$
be the logarithm map satisfying
where
![]() $d:R\to \Omega _{R}$
is the standard derivation.
$d:R\to \Omega _{R}$
is the standard derivation.
Let
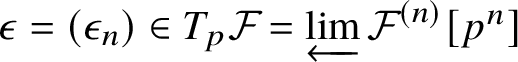 $\epsilon =(\epsilon _{n})\in T_{p}{\mathcal F}=\varprojlim {\mathcal F}^{(n)}[p^{n}]$
be a basis of the Tate module of
$\epsilon =(\epsilon _{n})\in T_{p}{\mathcal F}=\varprojlim {\mathcal F}^{(n)}[p^{n}]$
be a basis of the Tate module of
![]() ${\mathcal F}$
, where the limit is with respect to the transition maps
${\mathcal F}$
, where the limit is with respect to the transition maps
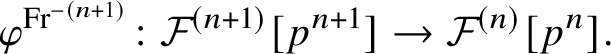 $$ \begin{align*} \varphi^{\mathrm{Fr}^{-(n+1)}}\colon {\mathcal F}^{(n+1)}[p^{n+1}]\to {\mathcal F}^{(n)}[p^{n}].\\[-15pt]\end{align*} $$
$$ \begin{align*} \varphi^{\mathrm{Fr}^{-(n+1)}}\colon {\mathcal F}^{(n+1)}[p^{n+1}]\to {\mathcal F}^{(n)}[p^{n}].\\[-15pt]\end{align*} $$
One can associate to
![]() $\epsilon $
and
$\epsilon $
and
![]() $\omega _{\mathcal F}$
a p-adic period
$\omega _{\mathcal F}$
a p-adic period
![]() $t_{\epsilon }\in B_{\text {cris}}^{+}$
such that
$t_{\epsilon }\in B_{\text {cris}}^{+}$
such that
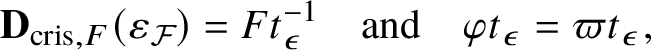 $$ \begin{align}{\mathbf D}_{\textrm{cris},F}(\varepsilon_{\mathcal F})=Ft_{\epsilon}^{-1} \quad\textrm{and}\quad\varphi t_{\epsilon}=\varpi t_{\epsilon},\\[-15pt]\nonumber\end{align} $$
$$ \begin{align}{\mathbf D}_{\textrm{cris},F}(\varepsilon_{\mathcal F})=Ft_{\epsilon}^{-1} \quad\textrm{and}\quad\varphi t_{\epsilon}=\varpi t_{\epsilon},\\[-15pt]\nonumber\end{align} $$
where
![]() $\varpi $
is the uniformiser in F such that
$\varpi $
is the uniformiser in F such that
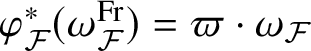 $\varphi _{\mathcal F}^{*}(\omega _{\mathcal F}^{\mathrm {Fr}})=\varpi \cdot \omega _{\mathcal F}$
(see [Reference Kobayashi30, §9.2]). For
$\varphi _{\mathcal F}^{*}(\omega _{\mathcal F}^{\mathrm {Fr}})=\varpi \cdot \omega _{\mathcal F}$
(see [Reference Kobayashi30, §9.2]). For
![]() $j\in \mathbf {Z}$
, the Lubin–Tate twist
$j\in \mathbf {Z}$
, the Lubin–Tate twist
 $V\langle j\rangle :=V\otimes _{L}\varepsilon _{\mathcal F}^{j}$
then satisfies
$V\langle j\rangle :=V\otimes _{L}\varepsilon _{\mathcal F}^{j}$
then satisfies
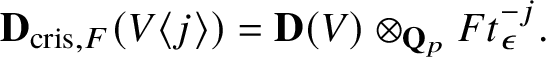 $$ \begin{align*} {\mathbf D}_{\textrm{cris},F}(V\langle j\rangle)={\mathbf D}(V)\otimes_{{\mathbf{Q}}_{p}} Ft_{\epsilon}^{-j}.\\[-15pt] \end{align*} $$
$$ \begin{align*} {\mathbf D}_{\textrm{cris},F}(V\langle j\rangle)={\mathbf D}(V)\otimes_{{\mathbf{Q}}_{p}} Ft_{\epsilon}^{-j}.\\[-15pt] \end{align*} $$
There is a derivation
![]() $\text {d}_{\epsilon }:{\mathscr D}_{\infty }(V\langle j\rangle )={\mathbf D}_{\text {cris},F}(V\langle j\rangle )\otimes _{\mathscr O}R^{\psi _{{\mathcal F}}=0}\to {\mathscr D}_{\infty }(V\langle j-1\rangle )$
given by
$\text {d}_{\epsilon }:{\mathscr D}_{\infty }(V\langle j\rangle )={\mathbf D}_{\text {cris},F}(V\langle j\rangle )\otimes _{\mathscr O}R^{\psi _{{\mathcal F}}=0}\to {\mathscr D}_{\infty }(V\langle j-1\rangle )$
given by
where
![]() $\partial \colon R\to R$
is defined by
$\partial \colon R\to R$
is defined by
![]() $df=\partial f\cdot \omega _{\mathcal F}$
. These give rise to the map
$df=\partial f\cdot \omega _{\mathcal F}$
. These give rise to the map
 $$ \begin{align} \widetilde{\Delta}\colon{\mathscr D}_{\infty}(V)\to \bigoplus_{j\in\mathbf{Z}}\frac{{\mathbf D}_{\textrm{cris},F}(V\langle -j\rangle)}{1-\varphi} \end{align} $$
$$ \begin{align} \widetilde{\Delta}\colon{\mathscr D}_{\infty}(V)\to \bigoplus_{j\in\mathbf{Z}}\frac{{\mathbf D}_{\textrm{cris},F}(V\langle -j\rangle)}{1-\varphi} \end{align} $$
sending
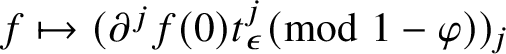 $f\mapsto (\partial ^{j}f(0)t_{\epsilon }^{j}\pmod {1-\varphi })_{j}$
.
$f\mapsto (\partial ^{j}f(0)t_{\epsilon }^{j}\pmod {1-\varphi })_{j}$
.
3.2 Perrin-Riou’s big exponential map
For a finite extension K over
![]() ${\mathbf {Q}}_{p}$
, let
${\mathbf {Q}}_{p}$
, let
 $$ \begin{align*}\exp_{K,V}\colon {\mathbf D}(V)\otimes_{{\mathbf{Q}}_{p}} K\to \textrm{H}^{1}(K,V)\end{align*} $$
$$ \begin{align*}\exp_{K,V}\colon {\mathbf D}(V)\otimes_{{\mathbf{Q}}_{p}} K\to \textrm{H}^{1}(K,V)\end{align*} $$
be Bloch–Kato’s exponential map [Reference Bloch and Kato7, §3]. In this subsection, we recall the main properties of Perrin-Riou’s map
![]() $\Omega _{V,h}$
interpolating
$\Omega _{V,h}$
interpolating
![]() $\exp _{K,V\langle j\rangle }$
over nonnegative
$\exp _{K,V\langle j\rangle }$
over nonnegative
![]() $j\in \mathbf {Z}$
.
$j\in \mathbf {Z}$
.
Let
![]() $V^{*}:=\operatorname {\mathrm {Hom}}_{L}(V,L(1))$
be the Kummer dual of V and denote by
$V^{*}:=\operatorname {\mathrm {Hom}}_{L}(V,L(1))$
be the Kummer dual of V and denote by
the K-linear extension of the de Rham pairing
Let
 $\exp ^{*}_{K,V}:\text {H}^{1}(K,V)\to {\mathbf D}(V)\otimes K$
be the Bloch–Kato dual exponential map, which is characterised uniquely by
$\exp ^{*}_{K,V}:\text {H}^{1}(K,V)\to {\mathbf D}(V)\otimes K$
be the Bloch–Kato dual exponential map, which is characterised uniquely by
for all
![]() $x\in {\mathbf D}(V^{*})\otimes K$
and
$x\in {\mathbf D}(V^{*})\otimes K$
and
![]() $y\in \text {H}^{1}(K,V)$
.
$y\in \text {H}^{1}(K,V)$
.
Choose a
![]() $\mathcal O_{L}$
-lattice
$\mathcal O_{L}$
-lattice
![]() $T\subset V$
stable under the Galois action and set
$T\subset V$
stable under the Galois action and set
 $\widehat {\text {H}}^{1}(F_{\infty },T)=\varprojlim _{n} \text {H}^{1}(F_{n},T)$
and
$\widehat {\text {H}}^{1}(F_{\infty },T)=\varprojlim _{n} \text {H}^{1}(F_{n},T)$
and
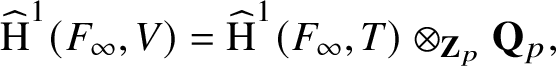 $$ \begin{align*} \widehat{\textrm{H}}^{1}(F_{\infty},V)=\widehat{\textrm{H}}^{1}(F_{\infty},T)\otimes_{\mathbf{Z}_{p}}{\mathbf{Q}}_{p}, \end{align*} $$
$$ \begin{align*} \widehat{\textrm{H}}^{1}(F_{\infty},V)=\widehat{\textrm{H}}^{1}(F_{\infty},T)\otimes_{\mathbf{Z}_{p}}{\mathbf{Q}}_{p}, \end{align*} $$
which does not depend on the choice of T. Denote by
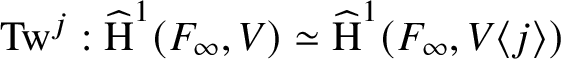 $$ \begin{align*} \textrm{Tw}^{j}:\widehat{\textrm{H}}^{1}(F_{\infty},V)\simeq \widehat{\textrm{H}}^{1}(F_{\infty},V\langle j\rangle) \end{align*} $$
$$ \begin{align*} \textrm{Tw}^{j}:\widehat{\textrm{H}}^{1}(F_{\infty},V)\simeq \widehat{\textrm{H}}^{1}(F_{\infty},V\langle j\rangle) \end{align*} $$
the twisting map by
![]() $\varepsilon _{\mathcal F}^{j}$
. For a nonnegative real number r, put
$\varepsilon _{\mathcal F}^{j}$
. For a nonnegative real number r, put
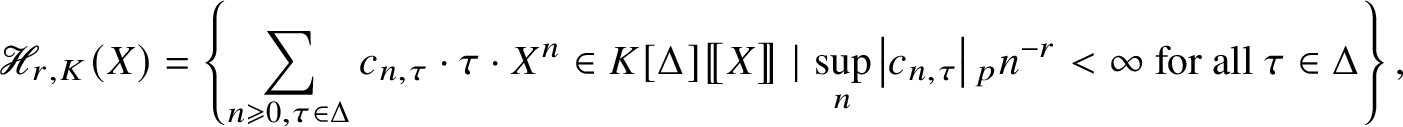
where
![]() $\left \vert \cdot \right \vert {}_{p}$
is the normalised valuation of K with
$\left \vert \cdot \right \vert {}_{p}$
is the normalised valuation of K with
![]() $\left \vert p\right \vert {}_{p}=p^{-1}$
. Let
$\left \vert p\right \vert {}_{p}=p^{-1}$
. Let
![]() ${\boldsymbol \gamma }$
be a topological generator of
${\boldsymbol \gamma }$
be a topological generator of
![]() $\Gamma ^{\mathcal F}_{\infty }$
and denote by
$\Gamma ^{\mathcal F}_{\infty }$
and denote by
![]() ${\mathscr H}_{r,K}(G_{\infty })$
the ring of elements
${\mathscr H}_{r,K}(G_{\infty })$
the ring of elements
![]() $\{f({\boldsymbol \gamma }-1)\colon f\in {\mathscr H}_{r,K}(X)\}$
, so, in particular,
$\{f({\boldsymbol \gamma }-1)\colon f\in {\mathscr H}_{r,K}(X)\}$
, so, in particular,
. Put
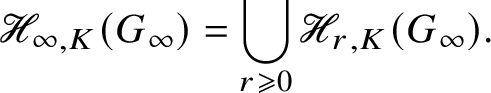 $$ \begin{align*}{\mathscr H}_{\infty,K}(G_{\infty})=\bigcup_{r\geqslant 0}{\mathscr H}_{r,K}(G_{\infty}).\end{align*} $$
$$ \begin{align*}{\mathscr H}_{\infty,K}(G_{\infty})=\bigcup_{r\geqslant 0}{\mathscr H}_{r,K}(G_{\infty}).\end{align*} $$
Define the map
by
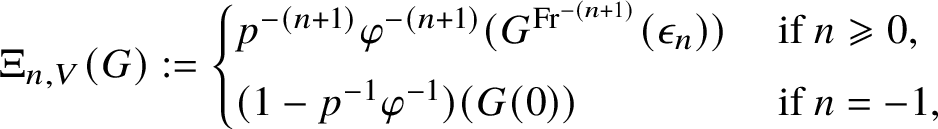 $$ \begin{align} \Xi_{n,V}(G):=\begin{cases}p^{-(n+1)}\varphi^{-(n+1)}(G^{\mathrm{Fr}^{-(n+1)}}(\epsilon_{n}))&\text{ if }n\geqslant 0,\\[0.1cm] (1-p^{-1}\varphi^{-1})(G(0))&\text{ if }n=-1,\end{cases} \end{align} $$
$$ \begin{align} \Xi_{n,V}(G):=\begin{cases}p^{-(n+1)}\varphi^{-(n+1)}(G^{\mathrm{Fr}^{-(n+1)}}(\epsilon_{n}))&\text{ if }n\geqslant 0,\\[0.1cm] (1-p^{-1}\varphi^{-1})(G(0))&\text{ if }n=-1,\end{cases} \end{align} $$
and let
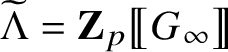 .
.
Theorem 3.2. Let
![]() $\epsilon =(\epsilon _{n})$
be a basis of
$\epsilon =(\epsilon _{n})$
be a basis of
![]() $T_{p}\mathcal {F}$
, let
$T_{p}\mathcal {F}$
, let
![]() $h>0$
be such that
$h>0$
be such that
![]() ${\mathbf D}(V)=\operatorname {\mathrm {Fil}}^{-h}{\mathbf D}(V)$
and assume that
${\mathbf D}(V)=\operatorname {\mathrm {Fil}}^{-h}{\mathbf D}(V)$
and assume that
![]() $\text {H}^{0}(F_{\infty },V)=0$
. There exists
$\text {H}^{0}(F_{\infty },V)=0$
. There exists
![]() $\widetilde \Lambda $
-linear ‘big exponential map’
$\widetilde \Lambda $
-linear ‘big exponential map’
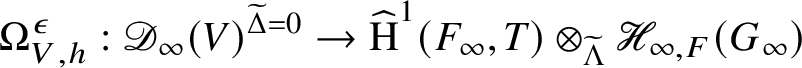 $$ \begin{align*}\Omega^{\epsilon}_{V,h}: {\mathscr D}_{\infty}(V)^{\widetilde{\Delta}=0}\to \widehat{\textrm{H}}^{1}(F_{\infty},T)\otimes_{\widetilde\Lambda} {\mathscr H}_{\infty,F}(G_{\infty})\end{align*} $$
$$ \begin{align*}\Omega^{\epsilon}_{V,h}: {\mathscr D}_{\infty}(V)^{\widetilde{\Delta}=0}\to \widehat{\textrm{H}}^{1}(F_{\infty},T)\otimes_{\widetilde\Lambda} {\mathscr H}_{\infty,F}(G_{\infty})\end{align*} $$
such that for every
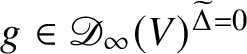 $g\in {\mathscr D}_{\infty }(V)^{\widetilde {\Delta }=0}$
and
$g\in {\mathscr D}_{\infty }(V)^{\widetilde {\Delta }=0}$
and
![]() $j\geqslant 1-h$
satisfies the interpolation property
$j\geqslant 1-h$
satisfies the interpolation property
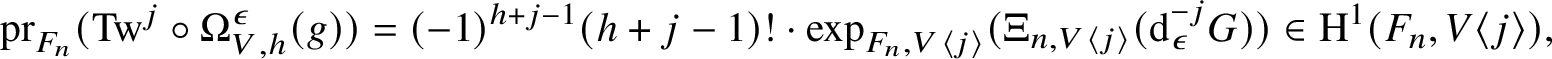 $$ \begin{align*} \textrm{pr}_{F_{n}}(\textrm{Tw}^{j}\circ\Omega^{\epsilon}_{V,h}(g))=(-1)^{h+j-1}(h+j-1)!\cdot \exp_{F_{n},V\langle j\rangle}(\Xi_{n,V\langle j\rangle}(\textrm{d}_{\epsilon}^{-j}G))\in \textrm{H}^{1}(F_{n},V\langle j\rangle), \end{align*} $$
$$ \begin{align*} \textrm{pr}_{F_{n}}(\textrm{Tw}^{j}\circ\Omega^{\epsilon}_{V,h}(g))=(-1)^{h+j-1}(h+j-1)!\cdot \exp_{F_{n},V\langle j\rangle}(\Xi_{n,V\langle j\rangle}(\textrm{d}_{\epsilon}^{-j}G))\in \textrm{H}^{1}(F_{n},V\langle j\rangle), \end{align*} $$
where
![]() $G\in {\mathbf D}(V)\otimes _{{\mathbf {Q}}_{p}} {\mathscr H}_{h,F}(X)$
is a solution of the equation
$G\in {\mathbf D}(V)\otimes _{{\mathbf {Q}}_{p}} {\mathscr H}_{h,F}(X)$
is a solution of the equation
Moreover, these maps satisfy
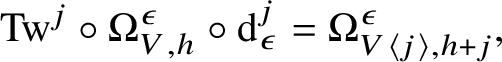 $$ \begin{align*} \textrm{Tw}^{j}\circ\Omega^{\epsilon}_{V,h}\circ \textrm{d}_{\epsilon}^{j}=\Omega^{\epsilon}_{V\langle j\rangle,h+j}, \end{align*} $$
$$ \begin{align*} \textrm{Tw}^{j}\circ\Omega^{\epsilon}_{V,h}\circ \textrm{d}_{\epsilon}^{j}=\Omega^{\epsilon}_{V\langle j\rangle,h+j}, \end{align*} $$
and if
![]() $j\leqslant -h$
, then
$j\leqslant -h$
, then
 $$ \begin{align*}\exp^{*}_{F_{n},V\langle j\rangle}(\textrm{pr}_{F_{n}}(\textrm{Tw}_{j}\circ\Omega^{\epsilon}_{V,h}(g)))=\frac{1}{(-h-j)!}\cdot \Xi_{n,V\langle j\rangle}(\textrm{d}_{\epsilon}^{-j}G))\in {\mathbf D}(V\langle j\rangle)\otimes_{{\mathbf{Q}}_{p}} F_{n},\end{align*} $$
$$ \begin{align*}\exp^{*}_{F_{n},V\langle j\rangle}(\textrm{pr}_{F_{n}}(\textrm{Tw}_{j}\circ\Omega^{\epsilon}_{V,h}(g)))=\frac{1}{(-h-j)!}\cdot \Xi_{n,V\langle j\rangle}(\textrm{d}_{\epsilon}^{-j}G))\in {\mathbf D}(V\langle j\rangle)\otimes_{{\mathbf{Q}}_{p}} F_{n},\end{align*} $$
and if
![]() $D_{[s]}\subset {\mathbf D}(V)$
is a
$D_{[s]}\subset {\mathbf D}(V)$
is a
![]() $\varphi $
-invariant subspace in which all
$\varphi $
-invariant subspace in which all
![]() $\varphi $
-eigenvalues have p-adic valuation at most s, then
$\varphi $
-eigenvalues have p-adic valuation at most s, then
![]() $\Omega _{V,h}^{\epsilon }$
maps
$\Omega _{V,h}^{\epsilon }$
maps
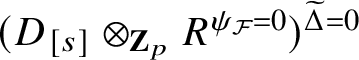 $(D_{[s]}\otimes _{\mathbf {Z}_{p}} R^{\psi _{{\mathcal F}}=0})^{\widetilde \Delta =0}$
into
$(D_{[s]}\otimes _{\mathbf {Z}_{p}} R^{\psi _{{\mathcal F}}=0})^{\widetilde \Delta =0}$
into
 $\widehat {\text {H}}^{1}(F_{\infty },T)\otimes _{\widetilde \Lambda }{\mathscr H}_{s+h,F}(G_{\infty })$
.
$\widehat {\text {H}}^{1}(F_{\infty },T)\otimes _{\widetilde \Lambda }{\mathscr H}_{s+h,F}(G_{\infty })$
.
Proof. For
![]() ${\mathcal F}=\widehat {\mathbf G}_{m}$
, the construction of
${\mathcal F}=\widehat {\mathbf G}_{m}$
, the construction of
![]() $\Omega _{V,h}^{\epsilon }$
and its interpolation property for
$\Omega _{V,h}^{\epsilon }$
and its interpolation property for
![]() $j\geqslant 1-h$
are due to Perrin-Riou [Reference Perrin-Riou36]; the interpolation formula for
$j\geqslant 1-h$
are due to Perrin-Riou [Reference Perrin-Riou36]; the interpolation formula for
![]() $j\leqslant -h$
is due to Colmez [Reference Colmez14]. The extension of these results to
$j\leqslant -h$
is due to Colmez [Reference Colmez14]. The extension of these results to
![]() $\mathbf {Z}_{p}$
-extensions arising from relative Lubin–Tate formal groups of height 1 is given in [Reference Kobayashi30, Appendix].
$\mathbf {Z}_{p}$
-extensions arising from relative Lubin–Tate formal groups of height 1 is given in [Reference Kobayashi30, Appendix].
3.3 The Coleman map
From now on, we assume that
 $$ \begin{align}{\mathscr D}_{\infty}(V)^{\widetilde\Delta=0}={\mathscr D}_{\infty}(V);\end{align} $$
$$ \begin{align}{\mathscr D}_{\infty}(V)^{\widetilde\Delta=0}={\mathscr D}_{\infty}(V);\end{align} $$
that is,
![]() $\widetilde \Delta =0$
(note that by (3.3), this is a condition on the
$\widetilde \Delta =0$
(note that by (3.3), this is a condition on the
![]() $\varphi $
-eigenvalues on
$\varphi $
-eigenvalues on
![]() ${\mathbf D}_{\text {cris},F}(V)$
), and for simplicity, for any field extension
${\mathbf D}_{\text {cris},F}(V)$
), and for simplicity, for any field extension
![]() $M/{\mathbf {Q}}_{p}$
we write
$M/{\mathbf {Q}}_{p}$
we write
![]() ${\mathscr H}_{M}$
for
${\mathscr H}_{M}$
for
![]() ${\mathscr H}_{0,M}(G_{\infty })$
. Let
${\mathscr H}_{0,M}(G_{\infty })$
. Let
be the pairing defined by
for all
![]() $\lambda _{1},\lambda _{2}\in {\mathscr H}_{F}$
.
$\lambda _{1},\lambda _{2}\in {\mathscr H}_{F}$
.
Recall that
![]() $F_{\infty }=\bigcup _{n}F_{n}$
, and let
$F_{\infty }=\bigcup _{n}F_{n}$
, and let
![]() $\langle -,-\rangle _{F_{n}}$
be the local Tate pairing
$\langle -,-\rangle _{F_{n}}$
be the local Tate pairing
![]() $\text {H}^{1}(F_{n},T^{*})\times \text {H}^{1}(F_{n},T)\rightarrow \mathcal {O}_{L}$
. Letting
$\text {H}^{1}(F_{n},T^{*})\times \text {H}^{1}(F_{n},T)\rightarrow \mathcal {O}_{L}$
. Letting
![]() $x=(x_{n})_{n}$
and
$x=(x_{n})_{n}$
and
![]() $y=(y_{n})_{n}$
be sequences in
$y=(y_{n})_{n}$
be sequences in
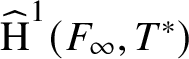 $\widehat {\text {H}}^{1}(F_{\infty },T^{*})$
and
$\widehat {\text {H}}^{1}(F_{\infty },T^{*})$
and
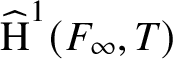 $\widehat {\text {H}}^{1}(F_{\infty },T)$
, define the
$\widehat {\text {H}}^{1}(F_{\infty },T)$
, define the
-linear pairing

by letting
![]() $\langle x,y\rangle _{F_{\infty }}$
be the limit of the elements
$\langle x,y\rangle _{F_{\infty }}$
be the limit of the elements
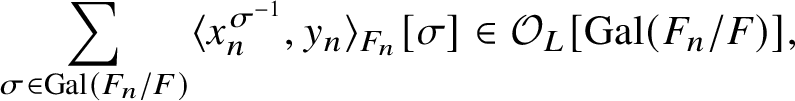 $$ \begin{align*} \sum_{\sigma\in\textrm{Gal}(F_{n}/F)}\langle x_{n}^{\sigma^{-1}},y_{n}\rangle_{F_{n}}[\sigma]\in\mathcal O_{L}[\textrm{Gal}(F_{n}/F)], \end{align*} $$
$$ \begin{align*} \sum_{\sigma\in\textrm{Gal}(F_{n}/F)}\langle x_{n}^{\sigma^{-1}},y_{n}\rangle_{F_{n}}[\sigma]\in\mathcal O_{L}[\textrm{Gal}(F_{n}/F)], \end{align*} $$
which are compatible under the natural projection maps
![]() $\mathcal O_{L}[\text {Gal}(F_{n+1}/F)]\rightarrow \mathcal O_{L}[\text {Gal}(F_{n}/F)]$
. After inverting p, this extends to a pairing
$\mathcal O_{L}[\text {Gal}(F_{n+1}/F)]\rightarrow \mathcal O_{L}[\text {Gal}(F_{n}/F)]$
. After inverting p, this extends to a pairing
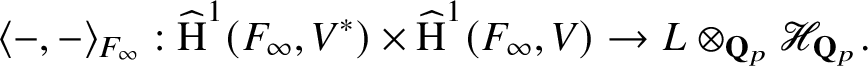 $$ \begin{align} \langle-,-\rangle_{F_{\infty}}:\widehat{\textrm{H}}^{1}(F_{\infty},V^{*})\times \widehat{\textrm{H}}^{1}(F_{\infty},V)\rightarrow L\otimes_{{\mathbf{Q}}_{p}}{\mathscr H}_{{\mathbf{Q}}_{p}}. \end{align} $$
$$ \begin{align} \langle-,-\rangle_{F_{\infty}}:\widehat{\textrm{H}}^{1}(F_{\infty},V^{*})\times \widehat{\textrm{H}}^{1}(F_{\infty},V)\rightarrow L\otimes_{{\mathbf{Q}}_{p}}{\mathscr H}_{{\mathbf{Q}}_{p}}. \end{align} $$
Definition 3.3. Let
![]() $\boldsymbol {e}\in R^{\psi _{\mathcal F}=0}$
be a
$\boldsymbol {e}\in R^{\psi _{\mathcal F}=0}$
be a
![]() -module generator, and let
-module generator, and let
![]() $\epsilon $
be a generator of
$\epsilon $
be a generator of
![]() $T_{p}{\mathcal F}$
. The Coleman map
$T_{p}{\mathcal F}$
. The Coleman map
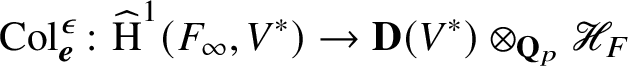 $$ \begin{align*} \textrm{Col}_{\boldsymbol{e}}^{\epsilon}\colon \widehat{\textrm{H}}^{1}(F_{\infty},V^{*})\to {\mathbf D}(V^{*})\otimes_{{\mathbf{Q}}_{p}} {\mathscr H}_{F} \end{align*} $$
$$ \begin{align*} \textrm{Col}_{\boldsymbol{e}}^{\epsilon}\colon \widehat{\textrm{H}}^{1}(F_{\infty},V^{*})\to {\mathbf D}(V^{*})\otimes_{{\mathbf{Q}}_{p}} {\mathscr H}_{F} \end{align*} $$
is the
![]() $L\otimes _{{\mathbf {Q}}_{p}}{\mathscr H}_{F}$
-linear map uniquely characterised by
$L\otimes _{{\mathbf {Q}}_{p}}{\mathscr H}_{F}$
-linear map uniquely characterised by
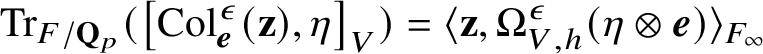 $$ \begin{align}\operatorname{\mathrm{Tr}}_{F/{\mathbf{Q}}_{p}}(\left[ \textrm{Col}_{\boldsymbol{e}}^{\epsilon}({\mathbf z}), \eta\right]_{V})=\langle {\mathbf z}, \Omega^{\epsilon}_{V,h}(\eta\otimes\boldsymbol{e})\rangle_{F_{\infty}} \end{align} $$
$$ \begin{align}\operatorname{\mathrm{Tr}}_{F/{\mathbf{Q}}_{p}}(\left[ \textrm{Col}_{\boldsymbol{e}}^{\epsilon}({\mathbf z}), \eta\right]_{V})=\langle {\mathbf z}, \Omega^{\epsilon}_{V,h}(\eta\otimes\boldsymbol{e})\rangle_{F_{\infty}} \end{align} $$
for all
![]() $\eta \in {\mathbf D}(V)$
.
$\eta \in {\mathbf D}(V)$
.
Let
![]() $\mathcal Q$
be the completion of
$\mathcal Q$
be the completion of
![]() ${\mathbf {Q}}_{p}^{\text {ur}}$
in
${\mathbf {Q}}_{p}^{\text {ur}}$
in
![]() $\mathbf {C}_{p}$
, with ring of integers
$\mathbf {C}_{p}$
, with ring of integers
![]() ${\mathcal W}$
, and set
${\mathcal W}$
, and set
![]() $F_{n}^{\text {ur}}=F_{n}{\mathbf {Q}}_{p}^{\text {ur}}$
for
$F_{n}^{\text {ur}}=F_{n}{\mathbf {Q}}_{p}^{\text {ur}}$
for
![]() $-1\leqslant n\leqslant \infty $
(so
$-1\leqslant n\leqslant \infty $
(so
![]() $F_{-1}^{\text {ur}}=F^{\text {ur}}$
). Let
$F_{-1}^{\text {ur}}=F^{\text {ur}}$
). Let
![]() $\sigma _{0}\in \operatorname {\mathrm {Gal}}(F_{\infty }^{\text {ur}}/{\mathbf {Q}}_{p})$
be such that
$\sigma _{0}\in \operatorname {\mathrm {Gal}}(F_{\infty }^{\text {ur}}/{\mathbf {Q}}_{p})$
be such that
![]() $\sigma _{0}|_{{\mathbf {Q}}_{p}^{\text {ur}}}=\mathrm {Fr}$
is the absolute Frobenius.
$\sigma _{0}|_{{\mathbf {Q}}_{p}^{\text {ur}}}=\mathrm {Fr}$
is the absolute Frobenius.
Fix an isomorphism
defined over
![]() ${\mathcal W}$
and let
${\mathcal W}$
and let
![]() be the map defined by
be the map defined by
![]() $\rho (f)=f\circ \rho ^{-1}$
, so
$\rho (f)=f\circ \rho ^{-1}$
, so
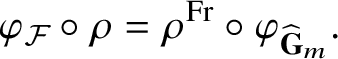 $$ \begin{align*}\varphi_{\mathcal F}\circ\rho=\rho^{\mathrm{Fr}}\circ\varphi_{\widehat{\mathbf G}_{m}}.\end{align*} $$
$$ \begin{align*}\varphi_{\mathcal F}\circ\rho=\rho^{\mathrm{Fr}}\circ\varphi_{\widehat{\mathbf G}_{m}}.\end{align*} $$
Fix also a
![]() -generator
-generator
![]() $\boldsymbol {e}\in R^{\psi _{\mathcal F}=0}$
and let
$\boldsymbol {e}\in R^{\psi _{\mathcal F}=0}$
and let
![]() be such that
be such that
![]() $\rho (1+X)=h_{\boldsymbol {e}}\cdot \boldsymbol {e}$
. Note that
$\rho (1+X)=h_{\boldsymbol {e}}\cdot \boldsymbol {e}$
. Note that
![]() $\boldsymbol {e}(0)\in \mathscr O^{\times }$
. Fix a sequence
$\boldsymbol {e}(0)\in \mathscr O^{\times }$
. Fix a sequence
![]() $(\zeta _{p^{n}})$
of primitive
$(\zeta _{p^{n}})$
of primitive
![]() $p^{n}$
th root of unity giving a generator of
$p^{n}$
th root of unity giving a generator of
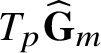 $T_{p}\widehat {\mathbf G}_{m}$
and let
$T_{p}\widehat {\mathbf G}_{m}$
and let
![]() $\epsilon =(\epsilon _{n})$
be the generator of
$\epsilon =(\epsilon _{n})$
be the generator of
![]() $T_{p}{\mathcal F}$
given by
$T_{p}{\mathcal F}$
given by
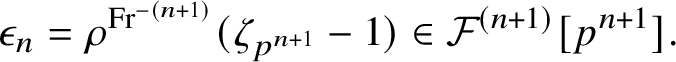 $$ \begin{align*}\epsilon_{n}=\rho^{\mathrm{Fr}^{-(n+1)}}(\zeta_{p^{n+1}}-1)\in{\mathcal F}^{(n+1)}[p^{n+1}].\end{align*} $$
$$ \begin{align*}\epsilon_{n}=\rho^{\mathrm{Fr}^{-(n+1)}}(\zeta_{p^{n+1}}-1)\in{\mathcal F}^{(n+1)}[p^{n+1}].\end{align*} $$
Let
![]() $t\in B_{\text {cris}}^{+}$
be the p-adic period as in Subsection 3.1 associated to the generator
$t\in B_{\text {cris}}^{+}$
be the p-adic period as in Subsection 3.1 associated to the generator
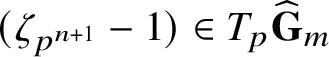 $(\zeta _{p^{n+1}}-1)\in T_{p}\widehat {\mathbf G}_{m}$
and the invariant differential
$(\zeta _{p^{n+1}}-1)\in T_{p}\widehat {\mathbf G}_{m}$
and the invariant differential
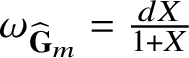 $\omega _{\widehat {\mathbf G}_{m}}=\frac {dX}{1+X}$
.
$\omega _{\widehat {\mathbf G}_{m}}=\frac {dX}{1+X}$
.
From now on, we suppose that
![]() $\operatorname {\mathrm {Fil}}^{-1}{\mathbf D}(V)={\mathbf D}(V)$
and
$\operatorname {\mathrm {Fil}}^{-1}{\mathbf D}(V)={\mathbf D}(V)$
and
![]() $\text {H}^{0}(F_{\infty },V)=0$
, so the big exponential map
$\text {H}^{0}(F_{\infty },V)=0$
, so the big exponential map
![]() $\Omega _{V,1}^{\epsilon }$
of Theorem 3.2 is defined. Let
$\Omega _{V,1}^{\epsilon }$
of Theorem 3.2 is defined. Let
![]() $\eta \in {\mathbf D}(V)$
be such that
$\eta \in {\mathbf D}(V)$
be such that
![]() $\varphi \eta =\alpha \eta $
and suppose that
$\varphi \eta =\alpha \eta $
and suppose that
![]() $\eta $
has slope s (i.e.,
$\eta $
has slope s (i.e.,
![]() $\left \vert \alpha \right \vert {}_{p}=p^{-s}$
). For every
$\left \vert \alpha \right \vert {}_{p}=p^{-s}$
). For every
 ${\mathbf z}\in \widehat {\text {H}}^{1}(F_{\infty },V^{*})$
, we define
${\mathbf z}\in \widehat {\text {H}}^{1}(F_{\infty },V^{*})$
, we define
 $$ \begin{align} \textrm{Col}^{\eta}({\mathbf z}):=\sum_{j=1}^{[F:{\mathbf{Q}}_{p}]}\left[ \textrm{Col}_{\boldsymbol{e}}^{\epsilon}({\mathbf z}^{\sigma_{0}^{-j}}), \eta\right]\cdot h_{\boldsymbol{e}}\cdot \sigma_{0}^{j}\in {\mathscr H}_{s+h,L\mathcal Q}(\widetilde G_{\infty}), \end{align} $$
$$ \begin{align} \textrm{Col}^{\eta}({\mathbf z}):=\sum_{j=1}^{[F:{\mathbf{Q}}_{p}]}\left[ \textrm{Col}_{\boldsymbol{e}}^{\epsilon}({\mathbf z}^{\sigma_{0}^{-j}}), \eta\right]\cdot h_{\boldsymbol{e}}\cdot \sigma_{0}^{j}\in {\mathscr H}_{s+h,L\mathcal Q}(\widetilde G_{\infty}), \end{align} $$
where
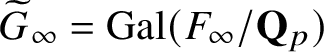 $\widetilde G_{\infty }=\operatorname {\mathrm {Gal}}(F_{\infty }/{\mathbf {Q}}_{p})$
and
$\widetilde G_{\infty }=\operatorname {\mathrm {Gal}}(F_{\infty }/{\mathbf {Q}}_{p})$
and
![]() $\left [ -, -\right ]\colon {\mathbf D}(V^{*})\otimes {\mathscr H}_{\mathcal Q} \times {\mathbf D}(V)\otimes {\mathscr H}_{\mathcal Q}\to {\mathscr H}_{L\mathcal Q}$
is the image of
$\left [ -, -\right ]\colon {\mathbf D}(V^{*})\otimes {\mathscr H}_{\mathcal Q} \times {\mathbf D}(V)\otimes {\mathscr H}_{\mathcal Q}\to {\mathscr H}_{L\mathcal Q}$
is the image of
![]() $\left [ -, -\right ]_{V}$
under the natural map
$\left [ -, -\right ]_{V}$
under the natural map
![]() $L\otimes _{{\mathbf {Q}}_{p}} {\mathscr H}_{\mathcal Q}\to {\mathscr H}_{L\mathcal Q}$
. We put
$L\otimes _{{\mathbf {Q}}_{p}} {\mathscr H}_{\mathcal Q}\to {\mathscr H}_{L\mathcal Q}$
. We put
 $$ \begin{align*} {\mathbf z}_{-j,n}:=\textrm{pr}_{F_{n}}(\textrm{Tw}^{-j}({\mathbf z}))\in\textrm{H}^{1}(F_{n},V^{*}\langle -j\rangle)\end{align*} $$
$$ \begin{align*} {\mathbf z}_{-j,n}:=\textrm{pr}_{F_{n}}(\textrm{Tw}^{-j}({\mathbf z}))\in\textrm{H}^{1}(F_{n},V^{*}\langle -j\rangle)\end{align*} $$
and say that a finite-order character
![]() $\chi $
of
$\chi $
of
![]() $\widetilde G_{\infty }$
has conductor
$\widetilde G_{\infty }$
has conductor
![]() $p^{n+1}$
if n is the smallest integer such that
$p^{n+1}$
if n is the smallest integer such that
![]() $\chi $
factors through
$\chi $
factors through
![]() $\operatorname {\mathrm {Gal}}(F_{n}/{\mathbf {Q}}_{p})$
.
$\operatorname {\mathrm {Gal}}(F_{n}/{\mathbf {Q}}_{p})$
.
Theorem 3.4. Let
 ${\mathbf z}\in \widehat {\text {H}}^{1}(F_{\infty },V^{*})$
and let
${\mathbf z}\in \widehat {\text {H}}^{1}(F_{\infty },V^{*})$
and let
![]() $\psi $
be a p-adic character of
$\psi $
be a p-adic character of
![]() $\widetilde G_{\infty }$
such that
$\widetilde G_{\infty }$
such that
 $\psi =\chi \varepsilon _{\mathcal F}^{j}$
with
$\psi =\chi \varepsilon _{\mathcal F}^{j}$
with
![]() $\chi $
a finite-order character of conductor
$\chi $
a finite-order character of conductor
![]() $p^{n+1}$
. If
$p^{n+1}$
. If
![]() $j<0$
, then
$j<0$
, then
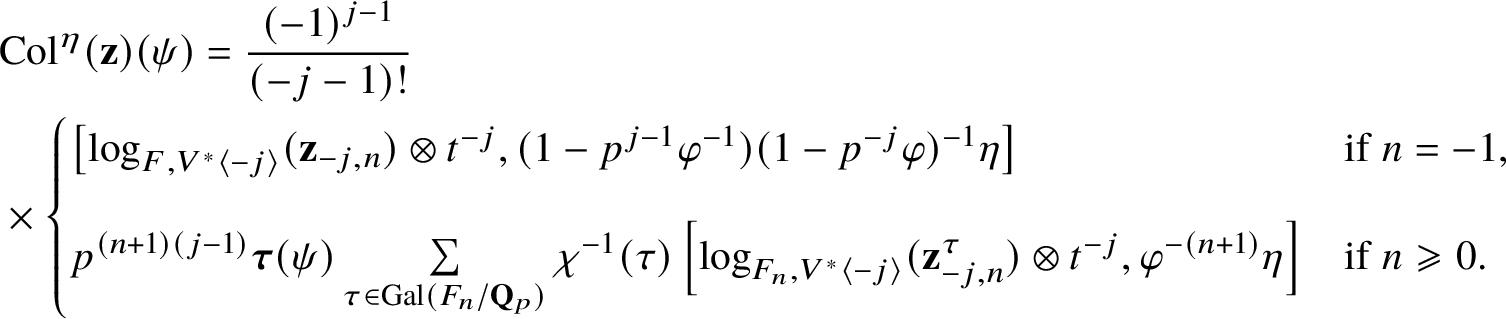 $$ \begin{align*} &\mathrm{Col}^{\eta}({\mathbf z})(\psi)=\frac{(-1)^{j-1}}{(-j-1)!}\\ &\times\begin{cases} \left[ \log_{F,V^{*}\langle -j\rangle}({\mathbf z}_{-j,n})\otimes t^{-j}, (1-p^{j-1}\varphi^{-1})(1-p^{-j}\varphi)^{-1}\eta\right]&\mathrm{ if\ }n=-1,\\[1 em] p^{(n+1){(j-1)}}\boldsymbol\tau(\psi)\sum\limits_{\tau\in\operatorname{\mathrm{Gal}}(F_{n}/{\mathbf{Q}}_{p})}\chi^{-1}(\tau)\left[ \log_{F_{n},V^{*}\langle -j\rangle}({\mathbf z}^{\tau}_{-j,n})\otimes t^{-j}, \varphi^{-(n+1)}\eta\right]&\mathrm{ if\ }n\geqslant 0. \end{cases} \end{align*} $$
$$ \begin{align*} &\mathrm{Col}^{\eta}({\mathbf z})(\psi)=\frac{(-1)^{j-1}}{(-j-1)!}\\ &\times\begin{cases} \left[ \log_{F,V^{*}\langle -j\rangle}({\mathbf z}_{-j,n})\otimes t^{-j}, (1-p^{j-1}\varphi^{-1})(1-p^{-j}\varphi)^{-1}\eta\right]&\mathrm{ if\ }n=-1,\\[1 em] p^{(n+1){(j-1)}}\boldsymbol\tau(\psi)\sum\limits_{\tau\in\operatorname{\mathrm{Gal}}(F_{n}/{\mathbf{Q}}_{p})}\chi^{-1}(\tau)\left[ \log_{F_{n},V^{*}\langle -j\rangle}({\mathbf z}^{\tau}_{-j,n})\otimes t^{-j}, \varphi^{-(n+1)}\eta\right]&\mathrm{ if\ }n\geqslant 0. \end{cases} \end{align*} $$
If
![]() $j\geqslant 0$
, then
$j\geqslant 0$
, then
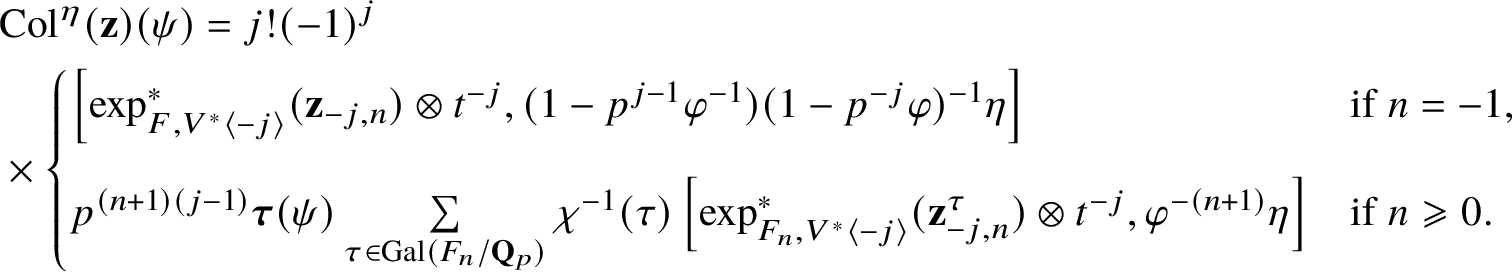 $$ \begin{align*} &\mathrm{Col}^{\eta}({\mathbf z})(\psi)=j!(-1)^{j}\\ &\times\begin{cases} \left[ \exp^{*}_{F,V^{*}\langle -j\rangle}({\mathbf z}_{-j,n})\otimes t^{-j}, (1-p^{j-1}\varphi^{-1})(1-p^{-j}\varphi)^{-1}\eta\right]&\mathrm{ if\ }n=-1,\\[1 em] p^{(n+1){(j-1)}}\boldsymbol\tau(\psi)\sum\limits_{\tau\in\operatorname{\mathrm{Gal}}(F_{n}/{\mathbf{Q}}_{p})}\chi^{-1}(\tau)\left[ \exp^{*}_{F_{n},V^{*}\langle -j\rangle}({\mathbf z}^{\tau}_{-j,n})\otimes t^{-j}, \varphi^{-(n+1)}\eta\right]&\mathrm{ if\ }n\geqslant 0. \end{cases} \end{align*} $$
$$ \begin{align*} &\mathrm{Col}^{\eta}({\mathbf z})(\psi)=j!(-1)^{j}\\ &\times\begin{cases} \left[ \exp^{*}_{F,V^{*}\langle -j\rangle}({\mathbf z}_{-j,n})\otimes t^{-j}, (1-p^{j-1}\varphi^{-1})(1-p^{-j}\varphi)^{-1}\eta\right]&\mathrm{ if\ }n=-1,\\[1 em] p^{(n+1){(j-1)}}\boldsymbol\tau(\psi)\sum\limits_{\tau\in\operatorname{\mathrm{Gal}}(F_{n}/{\mathbf{Q}}_{p})}\chi^{-1}(\tau)\left[ \exp^{*}_{F_{n},V^{*}\langle -j\rangle}({\mathbf z}^{\tau}_{-j,n})\otimes t^{-j}, \varphi^{-(n+1)}\eta\right]&\mathrm{ if\ }n\geqslant 0. \end{cases} \end{align*} $$
Here,
![]() $\boldsymbol \tau (\psi )$
is the Gauss sum defined by
$\boldsymbol \tau (\psi )$
is the Gauss sum defined by
 $$ \begin{align*}\boldsymbol\tau(\psi):=\sum_{\tau\in\operatorname{\mathrm{Gal}}(F^{\mathrm{ur}}_{n}/F^{\mathrm{ur}})}\psi\varepsilon_{\mathrm{cyc}}^{-j}(\tau\sigma_{0}^{n+1})\zeta_{p^{n+1}}^{\tau\sigma_{0}^{n+1}}.\end{align*} $$
$$ \begin{align*}\boldsymbol\tau(\psi):=\sum_{\tau\in\operatorname{\mathrm{Gal}}(F^{\mathrm{ur}}_{n}/F^{\mathrm{ur}})}\psi\varepsilon_{\mathrm{cyc}}^{-j}(\tau\sigma_{0}^{n+1})\zeta_{p^{n+1}}^{\tau\sigma_{0}^{n+1}}.\end{align*} $$
Proof. This follows from Theorem 3.2 by a direct computation (see [Reference Kobayashi30, Thm. 5.10] and [Reference Loeffler and Zerbes32, Thm. 4.15] for a related computation).
3.4 Diagonal cycles and theta elements
We now apply the local results of the preceding section to the global setting of Section 2. Assume that f,
![]() ${\boldsymbol {g}}=\boldsymbol {\theta }_{\psi }(S)$
and
${\boldsymbol {g}}=\boldsymbol {\theta }_{\psi }(S)$
and
![]() ${\boldsymbol {g}}^{*}=\boldsymbol {\theta }_{\psi ^{-1}}(S)$
are as in Subsection 2.4. Keeping the notations from Subsection 2.3, by [Reference Darmon and Rotger18, §1] (see also [Reference Darmon and Rotger19] and [Reference Bertolini, Seveso and Venerucci1]), there exists a class
${\boldsymbol {g}}^{*}=\boldsymbol {\theta }_{\psi ^{-1}}(S)$
are as in Subsection 2.4. Keeping the notations from Subsection 2.3, by [Reference Darmon and Rotger18, §1] (see also [Reference Darmon and Rotger19] and [Reference Bertolini, Seveso and Venerucci1]), there exists a class
 $$ \begin{align} \kappa(f,{{\boldsymbol{g}}{\boldsymbol{g}}^{*}})\in\textrm{H}^{1}(\mathbf{Q},\mathbb{V}^{\dagger}_{f,{{\boldsymbol{g}}{\boldsymbol{g}}^{*}}}(N)) \end{align} $$
$$ \begin{align} \kappa(f,{{\boldsymbol{g}}{\boldsymbol{g}}^{*}})\in\textrm{H}^{1}(\mathbf{Q},\mathbb{V}^{\dagger}_{f,{{\boldsymbol{g}}{\boldsymbol{g}}^{*}}}(N)) \end{align} $$
constructed from twisted diagonal cycles on the triple product of modular curves of tame level N.
Every triple of test vectors
![]() $\breve {\boldsymbol {F}}=(\breve {f},\breve {{\boldsymbol {g}}},\breve {{\boldsymbol {g}}}^{*})$
defines a
$\breve {\boldsymbol {F}}=(\breve {f},\breve {{\boldsymbol {g}}},\breve {{\boldsymbol {g}}}^{*})$
defines a
![]() $G_{\mathbf {Q}}$
-equivariant projection
$G_{\mathbf {Q}}$
-equivariant projection
 $\mathbb {V}^{\dagger }_{f,{{\boldsymbol {g}}{\boldsymbol {g}}}^{*}}(N)\rightarrow \mathbb {V}^{\dagger }_{f,{{\boldsymbol {g}}{\boldsymbol {g}}}^{*}}$
and we put
$\mathbb {V}^{\dagger }_{f,{{\boldsymbol {g}}{\boldsymbol {g}}}^{*}}(N)\rightarrow \mathbb {V}^{\dagger }_{f,{{\boldsymbol {g}}{\boldsymbol {g}}}^{*}}$
and we put
 $$ \begin{align} \kappa(\breve{f},{\breve{{\boldsymbol{g}}}\breve{{\boldsymbol{g}}}^{*}}):=\textrm{pr}_{\breve{\boldsymbol{F}}}(\kappa(f,{{\boldsymbol{g}}{\boldsymbol{g}}^{*}}))\in\textrm{H}^{1}(\mathbf{Q},\mathbb{V}^{\dagger}_{f,{{\boldsymbol{g}}{\boldsymbol{g}}^{*}}}), \end{align} $$
$$ \begin{align} \kappa(\breve{f},{\breve{{\boldsymbol{g}}}\breve{{\boldsymbol{g}}}^{*}}):=\textrm{pr}_{\breve{\boldsymbol{F}}}(\kappa(f,{{\boldsymbol{g}}{\boldsymbol{g}}^{*}}))\in\textrm{H}^{1}(\mathbf{Q},\mathbb{V}^{\dagger}_{f,{{\boldsymbol{g}}{\boldsymbol{g}}^{*}}}), \end{align} $$
where
 $\text {pr}_{\breve {\boldsymbol {F}}}:\text {H}^{1}(\mathbf {Q},\mathbb {V}^{\dagger }_{f,{{\boldsymbol {g}}{\boldsymbol {g}}^{*}}}(N))\to \text {H}^{1}(\mathbf {Q},\mathbb {V}^{\dagger }_{f,{{\boldsymbol {g}}{\boldsymbol {g}}^{*}}})$
is the induced map on cohomology.
$\text {pr}_{\breve {\boldsymbol {F}}}:\text {H}^{1}(\mathbf {Q},\mathbb {V}^{\dagger }_{f,{{\boldsymbol {g}}{\boldsymbol {g}}^{*}}}(N))\to \text {H}^{1}(\mathbf {Q},\mathbb {V}^{\dagger }_{f,{{\boldsymbol {g}}{\boldsymbol {g}}^{*}}})$
is the induced map on cohomology.
Since
 $\Psi _{T}^{1-\tau }$
gives the universal character of
$\Psi _{T}^{1-\tau }$
gives the universal character of
![]() $\text {Gal}(K_{\infty }/K)$
, by the
$\text {Gal}(K_{\infty }/K)$
, by the
![]() $G_{\mathbf {Q}}$
-isomorphism
$G_{\mathbf {Q}}$
-isomorphism
![]() $(2.4)$
and Shapiro’s lemma we have the identifications
$(2.4)$
and Shapiro’s lemma we have the identifications
 $$ \begin{align}\begin{aligned} \textrm{H}^{1}(\mathbf{Q},\mathbb{V}_{f,{\boldsymbol{g}}{\boldsymbol{g}}^{*}}^{\dagger})&\simeq\textrm{H}^{1}(\mathbf{Q},V_{f}(1)\otimes\textrm{Ind}_{K}^{\mathbf{Q}}\Psi_{T}^{1-\tau})\oplus\textrm{H}^{1}(\mathbf{Q},V_{f}(1)\otimes\operatorname{\mathrm{Ind}}_{K}^{\mathbf{Q}}\chi)\\ &\simeq\widehat{\textrm{H}}^{1}(K_{\infty},V_{f}(1))\oplus\textrm{H}^{1}(K,V_{f}(1)\otimes\chi). \end{aligned} \end{align} $$
$$ \begin{align}\begin{aligned} \textrm{H}^{1}(\mathbf{Q},\mathbb{V}_{f,{\boldsymbol{g}}{\boldsymbol{g}}^{*}}^{\dagger})&\simeq\textrm{H}^{1}(\mathbf{Q},V_{f}(1)\otimes\textrm{Ind}_{K}^{\mathbf{Q}}\Psi_{T}^{1-\tau})\oplus\textrm{H}^{1}(\mathbf{Q},V_{f}(1)\otimes\operatorname{\mathrm{Ind}}_{K}^{\mathbf{Q}}\chi)\\ &\simeq\widehat{\textrm{H}}^{1}(K_{\infty},V_{f}(1))\oplus\textrm{H}^{1}(K,V_{f}(1)\otimes\chi). \end{aligned} \end{align} $$
In the following, we write
according to this decomposition.
Let g and
![]() $g^{*}$
be the weight
$g^{*}$
be the weight
![]() $1$
eigenform
$1$
eigenform
![]() $\theta _{\psi }$
and
$\theta _{\psi }$
and
![]() $\theta _{\psi ^{-1}}$
, respectively, so that the specialisation of
$\theta _{\psi ^{-1}}$
, respectively, so that the specialisation of
![]() $({\boldsymbol {g}},{\boldsymbol {g}}^{*})$
at
$({\boldsymbol {g}},{\boldsymbol {g}}^{*})$
at
![]() $T=0$
(or, equivalently,
$T=0$
(or, equivalently,
![]() $S=\mathbf v-1$
) is a p-stabilisation of the pair
$S=\mathbf v-1$
) is a p-stabilisation of the pair
![]() $(g,g^{*})$
.
$(g,g^{*})$
.
Lemma 3.5. Assume that
![]() $L(f\otimes g\otimes g^{*},1)=0$
and that
$L(f\otimes g\otimes g^{*},1)=0$
and that
![]() $L(f/K\otimes \chi ,1)\neq 0$
. Then for every choice of test vectors
$L(f/K\otimes \chi ,1)\neq 0$
. Then for every choice of test vectors
![]() $\breve {\boldsymbol {F}}=(\breve {f},\breve {{\boldsymbol {g}}},\breve {{\boldsymbol {g}}^{*}})$
, we have
$\breve {\boldsymbol {F}}=(\breve {f},\breve {{\boldsymbol {g}}},\breve {{\boldsymbol {g}}^{*}})$
, we have
![]() $\kappa _{0}(\breve {f},{\breve {{\boldsymbol {g}}}\breve {{\boldsymbol {g}}^{*}}})=0$
.
$\kappa _{0}(\breve {f},{\breve {{\boldsymbol {g}}}\breve {{\boldsymbol {g}}^{*}}})=0$
.
Proof. Let
![]() ${\boldsymbol \kappa }=\kappa (\breve {f},\breve {{\boldsymbol {g}}}\breve {{\boldsymbol {g}}}^{*})$
and for every
${\boldsymbol \kappa }=\kappa (\breve {f},\breve {{\boldsymbol {g}}}\breve {{\boldsymbol {g}}}^{*})$
and for every
![]() $?\in \left \{f,{\boldsymbol {g}},{\boldsymbol {g}}^{*}\right \}$
, let
$?\in \left \{f,{\boldsymbol {g}},{\boldsymbol {g}}^{*}\right \}$
, let
![]() $\mathscr {F}^{+}V_?$
be the rank 1 subspace of
$\mathscr {F}^{+}V_?$
be the rank 1 subspace of
![]() $V_?$
fixed by the inertia group at p. By (3.12), in order to prove the result, it suffices to show that some specialisation of
$V_?$
fixed by the inertia group at p. By (3.12), in order to prove the result, it suffices to show that some specialisation of
![]() $\bf \kappa $
has trivial image in
$\bf \kappa $
has trivial image in
 $\text {H}^{1}(K,V_{f}(1)\otimes \chi )$
. Let
$\text {H}^{1}(K,V_{f}(1)\otimes \chi )$
. Let
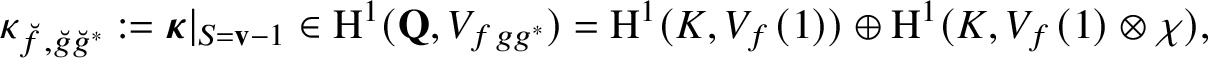 $$ \begin{align*} \kappa_{\breve{f},\breve{g}\breve{g}^{*}}:={\boldsymbol \kappa}\vert_{S=\mathbf{v}-1}\in\textrm{H}^{1}(\mathbf{Q},V_{fgg^{*}})=\textrm{H}^{1}(K,V_{f}(1))\oplus\textrm{H}^{1}(K,V_{f}(1)\otimes\chi), \end{align*} $$
$$ \begin{align*} \kappa_{\breve{f},\breve{g}\breve{g}^{*}}:={\boldsymbol \kappa}\vert_{S=\mathbf{v}-1}\in\textrm{H}^{1}(\mathbf{Q},V_{fgg^{*}})=\textrm{H}^{1}(K,V_{f}(1))\oplus\textrm{H}^{1}(K,V_{f}(1)\otimes\chi), \end{align*} $$
where
![]() $V_{fgg^{*}}:=V_{f}(1)\otimes V_{g}\otimes V_{g^{*}}$
. By looking at the Hodge–Tate weights, we see that the Bloch–Kato Selmer group
$V_{fgg^{*}}:=V_{f}(1)\otimes V_{g}\otimes V_{g^{*}}$
. By looking at the Hodge–Tate weights, we see that the Bloch–Kato Selmer group
 $\text {Sel}(\mathbf {Q},V_{fgg^{*}})\subset \text {H}^{1}(\mathbf {Q},V_{fgg^{*}})$
is given by
$\text {Sel}(\mathbf {Q},V_{fgg^{*}})\subset \text {H}^{1}(\mathbf {Q},V_{fgg^{*}})$
is given by
 $$ \begin{align*} \textrm{Sel}(\mathbf{Q},V_{fgg^{*}})=\textrm{ker}\bigg( \textrm{H}^{1}(\mathbf{Q},V_{fgg^{*}})\overset{\partial_{p}\circ\textrm{loc}_{p}}\rightarrow \textrm{H}^{1}({\mathbf{Q}}_{p},\mathscr{F}^{-}V_{f}(1)\otimes V_{g}\otimes V_{g^{*}})\bigg), \end{align*} $$
$$ \begin{align*} \textrm{Sel}(\mathbf{Q},V_{fgg^{*}})=\textrm{ker}\bigg( \textrm{H}^{1}(\mathbf{Q},V_{fgg^{*}})\overset{\partial_{p}\circ\textrm{loc}_{p}}\rightarrow \textrm{H}^{1}({\mathbf{Q}}_{p},\mathscr{F}^{-}V_{f}(1)\otimes V_{g}\otimes V_{g^{*}})\bigg), \end{align*} $$
where
![]() $\partial _{p}$
is the natural map induced by the projection
$\partial _{p}$
is the natural map induced by the projection
![]() $V_{f}\twoheadrightarrow \mathscr {F}^{-}V_{f}:=V_{f}/\mathscr {F}^{+}V_{f}$
(see, e.g., [Reference Darmon and Rotger18, p. 634]). Thus, it follows that
$V_{f}\twoheadrightarrow \mathscr {F}^{-}V_{f}:=V_{f}/\mathscr {F}^{+}V_{f}$
(see, e.g., [Reference Darmon and Rotger18, p. 634]). Thus, it follows that
The implications
![]() $L(f\otimes g\otimes g^{*},1)=0\Longrightarrow \kappa _{\breve {f},\breve {g}\breve {g}^{*}}\in \text {Sel}(\mathbf {Q},V_{fgg^{*}})$
and
$L(f\otimes g\otimes g^{*},1)=0\Longrightarrow \kappa _{\breve {f},\breve {g}\breve {g}^{*}}\in \text {Sel}(\mathbf {Q},V_{fgg^{*}})$
and
![]() $L(f/K\otimes \chi ,1)\neq 0\Longrightarrow \text {Sel}(K,V_{f}(1)\otimes \chi )=0$
, which follow from [Reference Darmon and Rotger18, Thm. C] and [Reference Chida and Hsieh12, Thm. 1], respectively, therefore yield the result.
$L(f/K\otimes \chi ,1)\neq 0\Longrightarrow \text {Sel}(K,V_{f}(1)\otimes \chi )=0$
, which follow from [Reference Darmon and Rotger18, Thm. C] and [Reference Chida and Hsieh12, Thm. 1], respectively, therefore yield the result.
Suppose from now on that
![]() $f^{\circ }\in S_{2}(\Gamma _{0}(N_{f}))$
is the newform associated to an elliptic curve
$f^{\circ }\in S_{2}(\Gamma _{0}(N_{f}))$
is the newform associated to an elliptic curve
![]() $E/\mathbf {Q}$
with good ordinary reduction at p. Thus,
$E/\mathbf {Q}$
with good ordinary reduction at p. Thus,
![]() $V_{f}(1)\simeq V_{p}E$
, and from (3.13) we obtain an Iwasawa cohomology class
$V_{f}(1)\simeq V_{p}E$
, and from (3.13) we obtain an Iwasawa cohomology class
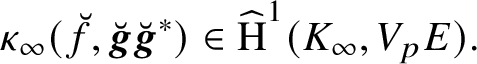 $$ \begin{align*} \kappa_{\infty}(\breve{f},\breve{{\boldsymbol{g}}}\breve{{\boldsymbol{g}}}^{*})\in\widehat{\textrm{H}}^{1}(K_{\infty},V_{p}E). \end{align*} $$
$$ \begin{align*} \kappa_{\infty}(\breve{f},\breve{{\boldsymbol{g}}}\breve{{\boldsymbol{g}}}^{*})\in\widehat{\textrm{H}}^{1}(K_{\infty},V_{p}E). \end{align*} $$
Set
![]() $V=V_{p}E$
for ease of notation. Note that
$V=V_{p}E$
for ease of notation. Note that
![]() $\operatorname {\mathrm {Fil}}^{-1}{\mathbf D}(V)={\mathbf D}(V)$
and, by the Weil pairing,
$\operatorname {\mathrm {Fil}}^{-1}{\mathbf D}(V)={\mathbf D}(V)$
and, by the Weil pairing,
![]() $V^{*}\simeq V$
. Let
$V^{*}\simeq V$
. Let
![]() ${\mathfrak P}$
be the prime of
${\mathfrak P}$
be the prime of
![]() $\overline {\mathbf {Q}}$
above p induced by our fixed embedding
$\overline {\mathbf {Q}}$
above p induced by our fixed embedding
![]() $\iota _{p}$
(inducing
$\iota _{p}$
(inducing
![]() $\frak {p}$
on K), and for any subfield
$\frak {p}$
on K), and for any subfield
![]() $H\subseteq \overline {\mathbf {Q}}$
denote by
$H\subseteq \overline {\mathbf {Q}}$
denote by
![]() $\hat H=H_{\mathfrak P}$
the completion of H with respect to
$\hat H=H_{\mathfrak P}$
the completion of H with respect to
![]() ${\mathfrak P}$
. Then
${\mathfrak P}$
. Then
![]() $\text {Gal}(\hat K_{\infty }/{\mathbf {Q}}_{p})$
is identified with the decomposition group of
$\text {Gal}(\hat K_{\infty }/{\mathbf {Q}}_{p})$
is identified with the decomposition group of
![]() $\mathfrak {P}$
in
$\mathfrak {P}$
in
![]() $\Gamma _{\infty }=\text {Gal}(K_{\infty }/K)$
.
$\Gamma _{\infty }=\text {Gal}(K_{\infty }/K)$
.
For any integer m, let
![]() $H_{m}$
be the ring class field of K of conductor m and put
$H_{m}$
be the ring class field of K of conductor m and put
![]() $F=\hat H_{c}$
for a fixed c prime to p. Let
$F=\hat H_{c}$
for a fixed c prime to p. Let
![]() $\varpi \in K$
be a generator of
$\varpi \in K$
be a generator of
![]() ${\mathfrak p}^{[F:{\mathbf {Q}}_{p}]}$
and let
${\mathfrak p}^{[F:{\mathbf {Q}}_{p}]}$
and let
![]() $F_{\infty }/F$
be the Lubin–Tate
$F_{\infty }/F$
be the Lubin–Tate
![]() $\mathbf {Z}_{p}$
-extension associated with the uniformiser
$\mathbf {Z}_{p}$
-extension associated with the uniformiser
![]() $\varpi /\overline {\varpi }\in \mathcal O_{F}$
(see [Reference Kobayashi30, §3.1]). As is well-known, we have
$\varpi /\overline {\varpi }\in \mathcal O_{F}$
(see [Reference Kobayashi30, §3.1]). As is well-known, we have
 $$ \begin{align*} F_{\infty}=\bigcup_{n=0}^{\infty}\hat H_{cp^{n}} \end{align*} $$
$$ \begin{align*} F_{\infty}=\bigcup_{n=0}^{\infty}\hat H_{cp^{n}} \end{align*} $$
(see, e.g., [Reference Shnidman42, Prop. 8.3]). In particular,
![]() $F_{\infty }$
contains
$F_{\infty }$
contains
![]() $\hat K_{\infty }$
.
$\hat K_{\infty }$
.
Let
![]() $\omega _{E}$
be the Néron differential of E, regarded as an element in
$\omega _{E}$
be the Néron differential of E, regarded as an element in
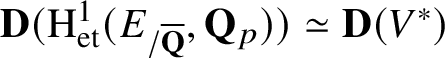 ${\mathbf D}(\text {H}_{\text {et}}^{1}(E_{/\overline {\mathbf {Q}}},{\mathbf {Q}}_{p}))\simeq {\mathbf D}(V^{*})$
. Let
${\mathbf D}(\text {H}_{\text {et}}^{1}(E_{/\overline {\mathbf {Q}}},{\mathbf {Q}}_{p}))\simeq {\mathbf D}(V^{*})$
. Let
![]() $\alpha _{p}\in \mathbf {Z}_{p}^{\times }$
be the p-adic unit eigenvalue of the Frobenius map
$\alpha _{p}\in \mathbf {Z}_{p}^{\times }$
be the p-adic unit eigenvalue of the Frobenius map
![]() $\varphi $
acting on
$\varphi $
acting on
![]() ${\mathbf D}(V)$
and let
${\mathbf D}(V)$
and let
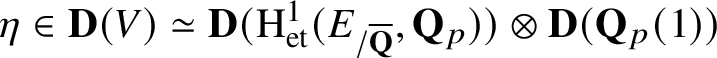 $\eta \in {\mathbf D}(V)\simeq {\mathbf D}(\text {H}^{1}_{\text {et}}(E_{/\overline {\mathbf {Q}}},{\mathbf {Q}}_{p}))\otimes {\mathbf D}({\mathbf {Q}}_{p}(1))$
be a
$\eta \in {\mathbf D}(V)\simeq {\mathbf D}(\text {H}^{1}_{\text {et}}(E_{/\overline {\mathbf {Q}}},{\mathbf {Q}}_{p}))\otimes {\mathbf D}({\mathbf {Q}}_{p}(1))$
be a
![]() $\varphi $
-eigenvector of slope
$\varphi $
-eigenvector of slope
![]() $-1$
such that
$-1$
such that
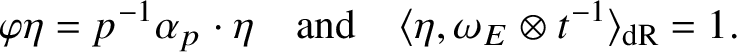 $$ \begin{align} \varphi \eta=p^{-1}\alpha_{p}\cdot\eta\quad\textrm{and}\quad \langle \eta, \omega_{E}\otimes t^{-1}\rangle_{\textrm{dR}}=1. \end{align} $$
$$ \begin{align} \varphi \eta=p^{-1}\alpha_{p}\cdot\eta\quad\textrm{and}\quad \langle \eta, \omega_{E}\otimes t^{-1}\rangle_{\textrm{dR}}=1. \end{align} $$
Finally, note that hypothesis (3.5) holds since
 $ {\mathbf D}(V)^{\varphi ^{[F:{\mathbf {Q}}_{p}]}=(\varpi /\overline {\varpi })^{j}}=0$
for any
$ {\mathbf D}(V)^{\varphi ^{[F:{\mathbf {Q}}_{p}]}=(\varpi /\overline {\varpi })^{j}}=0$
for any
![]() $j\in \mathbf {Z}$
, given that the
$j\in \mathbf {Z}$
, given that the
![]() $\varphi $
-eigenvalues of
$\varphi $
-eigenvalues of
![]() ${\mathbf D}(V)$
are p-Weil numbers, while
${\mathbf D}(V)$
are p-Weil numbers, while
![]() $\varpi /\overline {\varpi }$
is a
$\varpi /\overline {\varpi }$
is a
![]() $1$
-Weil number.
$1$
-Weil number.
The second part of the next result recasts the ‘explicit reciprocity law’ of [Reference Darmon and Rotger18, Thm. 5.3] (see also [Reference Darmon and Rotger19, Thm. 5.1] and [Reference Bertolini, Seveso and Venerucci1, Thm. A]) in terms of the Coleman map of Subsection 3.3.
Theorem 3.6. Assume that
![]() $L(f\otimes g\otimes g^{*},1)=0$
and that
$L(f\otimes g\otimes g^{*},1)=0$
and that
![]() $L(f/K\otimes \chi ,1)\neq 0$
. Then, for any test vectors
$L(f/K\otimes \chi ,1)\neq 0$
. Then, for any test vectors
![]() $(\breve {f},\breve {{\boldsymbol {g}}},\breve {{\boldsymbol {g}}}^{*})$
, we have
$(\breve {f},\breve {{\boldsymbol {g}}},\breve {{\boldsymbol {g}}}^{*})$
, we have
 $$ \begin{align*} \mathrm{Loc}_{\overline{\mathfrak{p}}}(\kappa_{\infty}(\breve{f},\breve{{\boldsymbol{g}}}\breve{{\boldsymbol{g}}}^{*}))=0 \end{align*} $$
$$ \begin{align*} \mathrm{Loc}_{\overline{\mathfrak{p}}}(\kappa_{\infty}(\breve{f},\breve{{\boldsymbol{g}}}\breve{{\boldsymbol{g}}}^{*}))=0 \end{align*} $$
and
 $$ \begin{align*} \mathrm{Col}^{\eta}(\mathrm{Loc}_{\mathfrak{p}}(\kappa_{\infty}(\breve{f},\breve{{\boldsymbol{g}}}\breve{{\boldsymbol{g}}}^{*})))= \mathscr{L}_{p}^{f}(\breve{f},{\breve{{\boldsymbol{g}}}\breve{{\boldsymbol{g}}}^{*}}) \cdot 2\alpha_{p}^{-1}(1-\alpha_{p}^{-1}\chi(\overline{{\mathfrak p}}))^{-1}. \end{align*} $$
$$ \begin{align*} \mathrm{Col}^{\eta}(\mathrm{Loc}_{\mathfrak{p}}(\kappa_{\infty}(\breve{f},\breve{{\boldsymbol{g}}}\breve{{\boldsymbol{g}}}^{*})))= \mathscr{L}_{p}^{f}(\breve{f},{\breve{{\boldsymbol{g}}}\breve{{\boldsymbol{g}}}^{*}}) \cdot 2\alpha_{p}^{-1}(1-\alpha_{p}^{-1}\chi(\overline{{\mathfrak p}}))^{-1}. \end{align*} $$
Proof. Let
 $\mathscr {F}^{++}\mathbb {V}_{f{\boldsymbol {g}}{\boldsymbol {g}}^{*}}^{\dagger }$
be the rank 4
$\mathscr {F}^{++}\mathbb {V}_{f{\boldsymbol {g}}{\boldsymbol {g}}^{*}}^{\dagger }$
be the rank 4
![]() $G_{{\mathbf {Q}}_{p}}$
-stable submodule of
$G_{{\mathbf {Q}}_{p}}$
-stable submodule of
 $\mathbb {V}_{f{\boldsymbol {g}}{\boldsymbol {g}}^{*}}^{\dagger }$
defined by
$\mathbb {V}_{f{\boldsymbol {g}}{\boldsymbol {g}}^{*}}^{\dagger }$
defined by
 $$ \begin{align*} \left[\mathscr{F}^{+}V\otimes\mathscr{F}^{+}V_{{\boldsymbol{g}}}\otimes V_{{\boldsymbol{g}}^{*}}+\mathscr{F}^{+}V\otimes V_{{\boldsymbol{g}}}\otimes \mathscr{F}^{+}V_{{\boldsymbol{g}}^{*}}+V\otimes \mathscr{F}^{+}V_{{\boldsymbol{g}}}\otimes \mathscr{F}^{+}V_{{\boldsymbol{g}}^{*}}\right]\otimes\mathcal X^{-1}. \end{align*} $$
$$ \begin{align*} \left[\mathscr{F}^{+}V\otimes\mathscr{F}^{+}V_{{\boldsymbol{g}}}\otimes V_{{\boldsymbol{g}}^{*}}+\mathscr{F}^{+}V\otimes V_{{\boldsymbol{g}}}\otimes \mathscr{F}^{+}V_{{\boldsymbol{g}}^{*}}+V\otimes \mathscr{F}^{+}V_{{\boldsymbol{g}}}\otimes \mathscr{F}^{+}V_{{\boldsymbol{g}}^{*}}\right]\otimes\mathcal X^{-1}. \end{align*} $$
The class
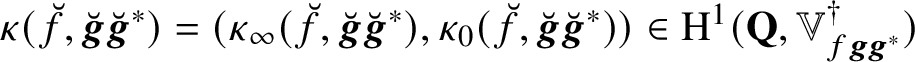 $\kappa (\breve {f},\breve {{\boldsymbol {g}}}\breve {{\boldsymbol {g}}}^{*})=(\kappa _{\infty }(\breve {f},\breve {{\boldsymbol {g}}}\breve {{\boldsymbol {g}}}^{*}),\kappa _{0}(\breve {f},\breve {{\boldsymbol {g}}}\breve {{\boldsymbol {g}}}^{*}))\in \text {H}^{1}(\mathbf {Q},\mathbb {V}_{f{\boldsymbol {g}}{\boldsymbol {g}}^{*}}^{\dagger })$
is known to land in the kernel of the composite map
$\kappa (\breve {f},\breve {{\boldsymbol {g}}}\breve {{\boldsymbol {g}}}^{*})=(\kappa _{\infty }(\breve {f},\breve {{\boldsymbol {g}}}\breve {{\boldsymbol {g}}}^{*}),\kappa _{0}(\breve {f},\breve {{\boldsymbol {g}}}\breve {{\boldsymbol {g}}}^{*}))\in \text {H}^{1}(\mathbf {Q},\mathbb {V}_{f{\boldsymbol {g}}{\boldsymbol {g}}^{*}}^{\dagger })$
is known to land in the kernel of the composite map
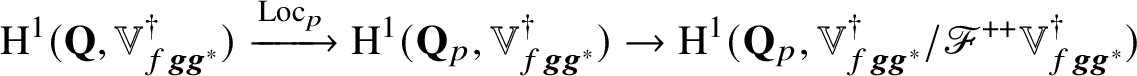 $$ \begin{align*} \textrm{H}^{1}(\mathbf{Q},\mathbb{V}_{f{\boldsymbol{g}}{\boldsymbol{g}}^{*}}^{\dagger})\xrightarrow{\textrm{Loc}_{p}} \textrm{H}^{1}({\mathbf{Q}}_{p},\mathbb{V}_{f{\boldsymbol{g}}{\boldsymbol{g}}^{*}}^{\dagger})\rightarrow\textrm{H}^{1}({\mathbf{Q}}_{p},\mathbb{V}_{f{\boldsymbol{g}}{\boldsymbol{g}}^{*}}^{\dagger}/\mathscr{F}^{++}\mathbb{V}_{f{\boldsymbol{g}}{\boldsymbol{g}}^{*}}^{\dagger})\nonumber \end{align*} $$
$$ \begin{align*} \textrm{H}^{1}(\mathbf{Q},\mathbb{V}_{f{\boldsymbol{g}}{\boldsymbol{g}}^{*}}^{\dagger})\xrightarrow{\textrm{Loc}_{p}} \textrm{H}^{1}({\mathbf{Q}}_{p},\mathbb{V}_{f{\boldsymbol{g}}{\boldsymbol{g}}^{*}}^{\dagger})\rightarrow\textrm{H}^{1}({\mathbf{Q}}_{p},\mathbb{V}_{f{\boldsymbol{g}}{\boldsymbol{g}}^{*}}^{\dagger}/\mathscr{F}^{++}\mathbb{V}_{f{\boldsymbol{g}}{\boldsymbol{g}}^{*}}^{\dagger})\nonumber \end{align*} $$
(see, e.g., [Reference Darmon and Rotger19, Prop. 5.8]). Using (2.4), we immediately find that
 $$ \begin{align*} \mathscr{F}^{++}\mathbb{V}_{f{\boldsymbol{g}}{\boldsymbol{g}}^{*}}^{\dagger}=V\otimes\Psi_{T}^{1-\tau}+\mathscr{F}^{+}V\otimes(\chi^{}+\chi^{-1}) \end{align*} $$
$$ \begin{align*} \mathscr{F}^{++}\mathbb{V}_{f{\boldsymbol{g}}{\boldsymbol{g}}^{*}}^{\dagger}=V\otimes\Psi_{T}^{1-\tau}+\mathscr{F}^{+}V\otimes(\chi^{}+\chi^{-1}) \end{align*} $$
and, therefore, identifying
![]() $G_{{\mathbf {Q}}_{p}}$
with
$G_{{\mathbf {Q}}_{p}}$
with
![]() $G_{K_{\mathfrak p}}$
via our fixed embedding
$G_{K_{\mathfrak p}}$
via our fixed embedding
 $\overline {\mathbf {Q}}\hookrightarrow \overline {\mathbf {Q}}_{p}$
, we obtain
$\overline {\mathbf {Q}}\hookrightarrow \overline {\mathbf {Q}}_{p}$
, we obtain
 $$ \begin{align*} \text{H}^{1}({\mathbf{Q}}_{p},\mathscr{F}^{++}\mathbb{V}_{f{\boldsymbol{g}}{\boldsymbol{g}}^{*}}^{\dagger})\simeq\text{H}^{1}(K_{{\mathfrak p}},V\otimes\Psi_{T}^{1-\tau})&\oplus\text{H}^{1}(K_{{\mathfrak p}},\mathscr{F}^{+}V\otimes\chi)\oplus\text{H}^{1}(K_{\overline{{\mathfrak p}}},\mathscr{F}^{+}V\otimes\chi). \end{align*} $$
$$ \begin{align*} \text{H}^{1}({\mathbf{Q}}_{p},\mathscr{F}^{++}\mathbb{V}_{f{\boldsymbol{g}}{\boldsymbol{g}}^{*}}^{\dagger})\simeq\text{H}^{1}(K_{{\mathfrak p}},V\otimes\Psi_{T}^{1-\tau})&\oplus\text{H}^{1}(K_{{\mathfrak p}},\mathscr{F}^{+}V\otimes\chi)\oplus\text{H}^{1}(K_{\overline{{\mathfrak p}}},\mathscr{F}^{+}V\otimes\chi). \end{align*} $$
This shows the vanishing of
 $\text {Loc}_{\overline {\mathfrak {p}}}(\kappa _{\infty }(\breve {f},\breve {{\boldsymbol {g}}}\breve {{\boldsymbol {g}}}^{*}))$
, and the second equality in the theorem follows from Lemma 3.5 and [Reference Darmon and Rotger18, Thm. 5.3].
$\text {Loc}_{\overline {\mathfrak {p}}}(\kappa _{\infty }(\breve {f},\breve {{\boldsymbol {g}}}\breve {{\boldsymbol {g}}}^{*}))$
, and the second equality in the theorem follows from Lemma 3.5 and [Reference Darmon and Rotger18, Thm. 5.3].
Corollary 3.7. Assume that
![]() $L(f\otimes g\otimes g^{*},1)=0$
and that
$L(f\otimes g\otimes g^{*},1)=0$
and that
![]() $L(f/K,\chi ,1)\neq 0$
. Let
$L(f/K,\chi ,1)\neq 0$
. Let
 $(\underline {\breve {f}},\underline {\breve {{\boldsymbol {g}}}},\underline {\breve {{\boldsymbol {g}}}}^{*})$
be the triple of test vectors from Theorem 2.1. Then
$(\underline {\breve {f}},\underline {\breve {{\boldsymbol {g}}}},\underline {\breve {{\boldsymbol {g}}}}^{*})$
be the triple of test vectors from Theorem 2.1. Then
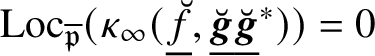 $\mathrm{Loc}_{\overline {\mathfrak {p}}}(\kappa _{\infty }(\underline {\breve {f}},\underline {\breve {{\boldsymbol {g}}}}\underline {\breve {{\boldsymbol {g}}}}^{*}))=0$
, and
$\mathrm{Loc}_{\overline {\mathfrak {p}}}(\kappa _{\infty }(\underline {\breve {f}},\underline {\breve {{\boldsymbol {g}}}}\underline {\breve {{\boldsymbol {g}}}}^{*}))=0$
, and
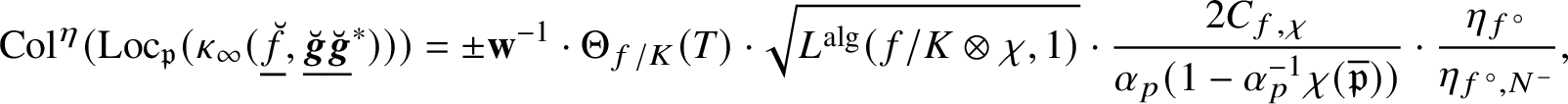 $$ \begin{align*} \mathrm{Col}^{\eta}(\mathrm{Loc}_{\mathfrak{p}}(\kappa_{\infty}(\underline{\breve{f}},\underline{\breve{{\boldsymbol{g}}}}\underline{\breve{{\boldsymbol{g}}}}^{*})))&=\pm\mathbf{w}^{-1}\cdot\Theta_{f/K}(T)\cdot \sqrt{L^{\mathrm{alg}}(f/K\otimes\chi,1)}\cdot\frac{2C_{f,\chi}}{\alpha_{p}(1-\alpha_{p}^{-1}\chi(\overline{{\mathfrak p}}))}\cdot\frac{\eta_{f^{\circ}}}{\eta_{f^{\circ},N^{-}}}, \end{align*} $$
$$ \begin{align*} \mathrm{Col}^{\eta}(\mathrm{Loc}_{\mathfrak{p}}(\kappa_{\infty}(\underline{\breve{f}},\underline{\breve{{\boldsymbol{g}}}}\underline{\breve{{\boldsymbol{g}}}}^{*})))&=\pm\mathbf{w}^{-1}\cdot\Theta_{f/K}(T)\cdot \sqrt{L^{\mathrm{alg}}(f/K\otimes\chi,1)}\cdot\frac{2C_{f,\chi}}{\alpha_{p}(1-\alpha_{p}^{-1}\chi(\overline{{\mathfrak p}}))}\cdot\frac{\eta_{f^{\circ}}}{\eta_{f^{\circ},N^{-}}}, \end{align*} $$
where
![]() and
and
![]() $C_{f,\chi }\in K(\chi ,\alpha _{p})^{\times }$
are as in Proposition 2.5.
$C_{f,\chi }\in K(\chi ,\alpha _{p})^{\times }$
are as in Proposition 2.5.
Remark 3.8. Corollary 3.7 places for the first time
![]() $\Theta _{f/K}(T)$
within the landscape of Perrin-Riou’s vision [Reference Perrin-Riou37], whereby p-adic L-functions ought to arise as the image of p-adic families of special cohomology classes under generalised Coleman power series maps. For a different class of anticyclotomic p-adic L-functions introduced by Bertolini–Darmon–Prasanna [Reference Bertolini, Darmon and Prasanna6], a similar result was obtained by the authors in [Reference Castella and Hsieh11, Reference Castella10].
$\Theta _{f/K}(T)$
within the landscape of Perrin-Riou’s vision [Reference Perrin-Riou37], whereby p-adic L-functions ought to arise as the image of p-adic families of special cohomology classes under generalised Coleman power series maps. For a different class of anticyclotomic p-adic L-functions introduced by Bertolini–Darmon–Prasanna [Reference Bertolini, Darmon and Prasanna6], a similar result was obtained by the authors in [Reference Castella and Hsieh11, Reference Castella10].
4 Anticyclotomic derived p-adic heights
The main result of this section is Theorem 4.5, giving a formula for the anticyclotomic derived p-adic heights in terms of the Coleman map introduced before. This generalises a formula of [Reference Rubin40] to arbitrary rank.
4.1 The general theory
Initiated in [Reference Bertolini and Darmon3] and further developed in [Reference Howard26], the theory of derived p-adic heights relates the degeneracies of the p-adic height to the failure of the
![]() $p^{\infty }$
-Selmer group of elliptic curves over a
$p^{\infty }$
-Selmer group of elliptic curves over a
![]() $\mathbf {Z}_{p}$
-extension to be semi-simple as an Iwasawa module. Derived p-adic heights seem to have been rarely used for arithmetic applications in the previous literature,Footnote
1
but they will play a key role in the proof of our results. In this section, we briefly recall the results from [Reference Howard26] (with a slight generalisation) that we will need.
$\mathbf {Z}_{p}$
-extension to be semi-simple as an Iwasawa module. Derived p-adic heights seem to have been rarely used for arithmetic applications in the previous literature,Footnote
1
but they will play a key role in the proof of our results. In this section, we briefly recall the results from [Reference Howard26] (with a slight generalisation) that we will need.
Let E be an elliptic curve over
![]() $\mathbf {Q}$
of conductor N with good ordinary reduction at
$\mathbf {Q}$
of conductor N with good ordinary reduction at
![]() $p>2$
. For any number field F, let
$p>2$
. For any number field F, let
 $\text {Sel}_{p^{r}}(E/F)\subseteq \text {H}^{1}(F,E[p^{r}])$
be the
$\text {Sel}_{p^{r}}(E/F)\subseteq \text {H}^{1}(F,E[p^{r}])$
be the
![]() $p^{r}$
-Selmer group of E over F and put
$p^{r}$
-Selmer group of E over F and put
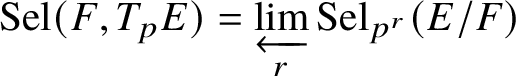 $$ \begin{align*} \textrm{Sel}(F,T_{p}E)=\varprojlim_{r}\textrm{Sel}_{p^{r}}(E/F) \end{align*} $$
$$ \begin{align*} \textrm{Sel}(F,T_{p}E)=\varprojlim_{r}\textrm{Sel}_{p^{r}}(E/F) \end{align*} $$
and
![]() $\text {Sel}(F,V_{p}E)=\text {Sel}(F,T_{p}E)\otimes _{\mathbf {Z}_{p}}{\mathbf {Q}}_{p}$
. Let K be an imaginary quadratic field of discriminant prime to
$\text {Sel}(F,V_{p}E)=\text {Sel}(F,T_{p}E)\otimes _{\mathbf {Z}_{p}}{\mathbf {Q}}_{p}$
. Let K be an imaginary quadratic field of discriminant prime to
![]() $Np$
and let
$Np$
and let
![]() $K_{\infty }/K$
be the anticyclotomic
$K_{\infty }/K$
be the anticyclotomic
![]() $\mathbf {Z}_{p}$
-extension of K. Denote by
$\mathbf {Z}_{p}$
-extension of K. Denote by
![]() $K_{n}$
the subsection of
$K_{n}$
the subsection of
![]() $K_{\infty }$
with
$K_{\infty }$
with
![]() $[K_{n}\colon K]=p^{n}$
and put
$[K_{n}\colon K]=p^{n}$
and put
 $$ \begin{align*} \textrm{Sel}_{p^{\infty}}(E/K_{\infty})=\varinjlim_{n}\textrm{Sel}_{p^{\infty}}(E/K_{n}). \end{align*} $$
$$ \begin{align*} \textrm{Sel}_{p^{\infty}}(E/K_{\infty})=\varinjlim_{n}\textrm{Sel}_{p^{\infty}}(E/K_{n}). \end{align*} $$
Finally, let
![]() be the anticyclotomic Iwasawa algebra and denote by
be the anticyclotomic Iwasawa algebra and denote by
![]() $J\subseteq \Lambda $
the augmentation ideal.
$J\subseteq \Lambda $
the augmentation ideal.
Theorem 4.1. Let
![]() $N^{-}$
be the largest factor of N divisible only by primes that are inert in K, and suppose that
$N^{-}$
be the largest factor of N divisible only by primes that are inert in K, and suppose that
-
•
 $N^{-}$
is squarefree,
$N^{-}$
is squarefree, -
•
 $E[p]$
is ramified at every prime
$E[p]$
is ramified at every prime
 $q\vert N^{-}$
.
$q\vert N^{-}$
.
Then there is a filtration
 $$ \begin{align*} \textrm{Sel}(K,V_{p}E)=S_{p}^{(1)}(E/K)\supseteq S_{p}^{(2)}(E/K)\supseteq\cdots\supseteq S_{p}^{(i)}(E/K)\supseteq\cdots \end{align*} $$
$$ \begin{align*} \textrm{Sel}(K,V_{p}E)=S_{p}^{(1)}(E/K)\supseteq S_{p}^{(2)}(E/K)\supseteq\cdots\supseteq S_{p}^{(i)}(E/K)\supseteq\cdots \end{align*} $$
and a sequence of height pairings
 $$ \begin{align*} h_{p}^{(i)}: S_{p}^{(i)}(E/K)\times S_{p}^{(i)}(E/K)\to (J^{i}/J^{i+1})\otimes_{\mathbf{Z}_{p}}{\mathbf{Q}}_{p} \end{align*} $$
$$ \begin{align*} h_{p}^{(i)}: S_{p}^{(i)}(E/K)\times S_{p}^{(i)}(E/K)\to (J^{i}/J^{i+1})\otimes_{\mathbf{Z}_{p}}{\mathbf{Q}}_{p} \end{align*} $$
with the following properties:
-
(a)
 $S_{p}^{(i+1)}(E/K)$
is the null-space of
$S_{p}^{(i+1)}(E/K)$
is the null-space of
 $h_{p}^{(i)}$
.
$h_{p}^{(i)}$
. -
(b)
 $S_{p}^{(\infty )}(E/K):=\bigcap _{i\geqslant 1}S_{p}^{(i)}(E/K)$
is the subspace of
$S_{p}^{(\infty )}(E/K):=\bigcap _{i\geqslant 1}S_{p}^{(i)}(E/K)$
is the subspace of
 $\mathrm{Sel}(K,V_{p}E)$
consisting of universal norms for
$\mathrm{Sel}(K,V_{p}E)$
consisting of universal norms for
 $K_{\infty }/K$
: where
$K_{\infty }/K$
: where $$ \begin{align*} S_{p}^{(\infty)}(E/K)=\bigcap_{n=1}^{\infty}\mathrm{cor}_{K_{n}/K}(\mathrm{Sel}(K_{n},V_{p}E)), \end{align*} $$
$$ \begin{align*} S_{p}^{(\infty)}(E/K)=\bigcap_{n=1}^{\infty}\mathrm{cor}_{K_{n}/K}(\mathrm{Sel}(K_{n},V_{p}E)), \end{align*} $$
 $\mathrm{cor}_{K_{n}/K}:\mathrm{Sel}(K_{n},V_{p}E)\rightarrow \mathrm{Sel}(K,V_{p}E)$
is the corestriction map.
$\mathrm{cor}_{K_{n}/K}:\mathrm{Sel}(K_{n},V_{p}E)\rightarrow \mathrm{Sel}(K,V_{p}E)$
is the corestriction map.
-
(c)
 $h_{p}^{(i)}$
is symmetric (respectively alternating) for i odd (respectively i even).
$h_{p}^{(i)}$
is symmetric (respectively alternating) for i odd (respectively i even). -
(d)
 $h_{p}^{(i)}(x^{\tau },y^{\tau })=(-1)^{i}h_{p}^{(i)}(x,y)$
, where
$h_{p}^{(i)}(x^{\tau },y^{\tau })=(-1)^{i}h_{p}^{(i)}(x,y)$
, where
 $\tau \in \mathrm{Gal}(K/\mathbf {Q})$
is complex conjugation.
$\tau \in \mathrm{Gal}(K/\mathbf {Q})$
is complex conjugation. -
(e) Let
Then there is a $$ \begin{align*} e_{i}:=\begin{cases} {\mathrm{dim}}_{{\mathbf{Q}}_{p}}(S_{p}^{(i)}(E/K)/S_{p}^{(i+1)}(E/K))&\mbox{if }i<\infty,\\[0.1cm] {\mathrm{dim}}_{{\mathbf{Q}}_{p}}S_{p}^{(\infty)}(E/K)&\mbox{if }i=\infty. \end{cases} \end{align*} $$
$$ \begin{align*} e_{i}:=\begin{cases} {\mathrm{dim}}_{{\mathbf{Q}}_{p}}(S_{p}^{(i)}(E/K)/S_{p}^{(i+1)}(E/K))&\mbox{if }i<\infty,\\[0.1cm] {\mathrm{dim}}_{{\mathbf{Q}}_{p}}S_{p}^{(\infty)}(E/K)&\mbox{if }i=\infty. \end{cases} \end{align*} $$
 $\Lambda $
-module pseudo-isomorphism with
$\Lambda $
-module pseudo-isomorphism with $$ \begin{align*} \mathrm{Sel}_{p^{\infty}}(E/K_{\infty})^{\vee}\sim\left((\Lambda/J)^{\oplus e_{1}}\oplus\cdots\oplus(\Lambda/J^{i})^{\oplus e_{i}}\oplus\cdots\right)\oplus\Lambda^{\oplus e_{\infty}} \oplus M^{\prime} \end{align*} $$
$$ \begin{align*} \mathrm{Sel}_{p^{\infty}}(E/K_{\infty})^{\vee}\sim\left((\Lambda/J)^{\oplus e_{1}}\oplus\cdots\oplus(\Lambda/J^{i})^{\oplus e_{i}}\oplus\cdots\right)\oplus\Lambda^{\oplus e_{\infty}} \oplus M^{\prime} \end{align*} $$
 $M^{\prime }$
a torsion
$M^{\prime }$
a torsion
 $\Lambda $
-module with characteristic ideal prime-to-J.
$\Lambda $
-module with characteristic ideal prime-to-J.
Proof. This follows from Theorem 4.2 and Corollary 4.3 of [Reference Howard26] when
![]() $N^{-}=1$
. We explain how to extend the result to squarefree
$N^{-}=1$
. We explain how to extend the result to squarefree
![]() $N^{-}$
under the above hypothesis on
$N^{-}$
under the above hypothesis on
![]() $E[p]$
.
$E[p]$
.
Following the discussion in [Reference Howard26, §3] and adopting the notations there, we see that it suffices to show the vanishing of
 $$ \begin{align} \textrm{H}^{1}_{\textrm{ur}}(K_{v},\mathbf{S}[p^{k}]):=\textrm{ker}\big(\textrm{H}^{1}(K_{v},\mathbf{S}[p^{k}])\rightarrow\textrm{H}^{1}(K_{v}^{\textrm{ur}},\mathbf{S}[p^{k}])\big) \end{align} $$
$$ \begin{align} \textrm{H}^{1}_{\textrm{ur}}(K_{v},\mathbf{S}[p^{k}]):=\textrm{ker}\big(\textrm{H}^{1}(K_{v},\mathbf{S}[p^{k}])\rightarrow\textrm{H}^{1}(K_{v}^{\textrm{ur}},\mathbf{S}[p^{k}])\big) \end{align} $$
for every prime
![]() $v\nmid p$
inert in K, where
$v\nmid p$
inert in K, where
 $\mathbf {S}[p^{k}]=\varinjlim _{n}\text {Ind}_{K_{n}/K}E[p^{k}]$
. Since such primes v split completely in
$\mathbf {S}[p^{k}]=\varinjlim _{n}\text {Ind}_{K_{n}/K}E[p^{k}]$
. Since such primes v split completely in
![]() $K_{\infty }/K$
, by Shapiro’s lemma and inflation-restriction we find
$K_{\infty }/K$
, by Shapiro’s lemma and inflation-restriction we find
 $$ \begin{align} \begin{aligned} \textrm{H}^{1}_{\textrm{ur}}(K_{v},\mathbf{S}[p^{k}])&\simeq \textrm{ker}\big(\textrm{H}^{1}(K_{v},E[p^{k}])\otimes\Lambda^{\vee}\rightarrow\textrm{H}^{1}(K_{v}^{\textrm{ur}},E[p^{k}])\otimes\Lambda^{\vee}\big)\\ &\simeq\textrm{H}^{1}(\mathbf{F}_{v},E[p^{k}]^{I_{v}})\otimes\Lambda^{\vee}\\ &=(E[p^{k}]^{I_{v}}/(\textrm{Fr}_{v}-1)E[p^{k}]^{I_{v}})\otimes\Lambda^{\vee}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \textrm{H}^{1}_{\textrm{ur}}(K_{v},\mathbf{S}[p^{k}])&\simeq \textrm{ker}\big(\textrm{H}^{1}(K_{v},E[p^{k}])\otimes\Lambda^{\vee}\rightarrow\textrm{H}^{1}(K_{v}^{\textrm{ur}},E[p^{k}])\otimes\Lambda^{\vee}\big)\\ &\simeq\textrm{H}^{1}(\mathbf{F}_{v},E[p^{k}]^{I_{v}})\otimes\Lambda^{\vee}\\ &=(E[p^{k}]^{I_{v}}/(\textrm{Fr}_{v}-1)E[p^{k}]^{I_{v}})\otimes\Lambda^{\vee}, \end{aligned} \end{align} $$
where
![]() $\mathbf {F}_{v}$
is the residue field of
$\mathbf {F}_{v}$
is the residue field of
![]() $K_{v}$
,
$K_{v}$
,
![]() $\text {Fr}_{v}$
is a Frobenius element at v and
$\text {Fr}_{v}$
is a Frobenius element at v and
![]() $\Lambda ^{\vee }=\text {Hom}_{\mathbf {Z}_{p}}(\Lambda ,{\mathbf {Q}}_{p}/\mathbf {Z}_{p})$
.
$\Lambda ^{\vee }=\text {Hom}_{\mathbf {Z}_{p}}(\Lambda ,{\mathbf {Q}}_{p}/\mathbf {Z}_{p})$
.
Since
![]() $N^{-}$
is squarefree, any prime v as above is a prime of multiplicative reduction for E, so by Tate’s uniformisation we have
$N^{-}$
is squarefree, any prime v as above is a prime of multiplicative reduction for E, so by Tate’s uniformisation we have
 $$ \begin{align*} E[p^{\infty}]\sim\left(\begin{array}{cc}\varepsilon_{\textrm{}}&*\\ 0&1\end{array}\right) \end{align*} $$
$$ \begin{align*} E[p^{\infty}]\sim\left(\begin{array}{cc}\varepsilon_{\textrm{}}&*\\ 0&1\end{array}\right) \end{align*} $$
as
![]() $G_{K_{v}}$
-modules, where
$G_{K_{v}}$
-modules, where
![]() $\varepsilon $
is the p-adic cyclotomic character. Since
$\varepsilon $
is the p-adic cyclotomic character. Since
![]() $\bar {\rho }_{E,p}$
is ramified at v, the image of ‘
$\bar {\rho }_{E,p}$
is ramified at v, the image of ‘
![]() $*$
’ in the above matrix generates
$*$
’ in the above matrix generates
![]() ${\mathbf {Q}}_{p}/\mathbf {Z}_{p}$
. Thus, we see that
${\mathbf {Q}}_{p}/\mathbf {Z}_{p}$
. Thus, we see that
which by
![]() $(4.2)$
implies the vanishing of
$(4.2)$
implies the vanishing of
![]() $\text {H}^{1}_{\text {ur}}(K_{v},\mathbf {S}[p^{k}])$
.
$\text {H}^{1}_{\text {ur}}(K_{v},\mathbf {S}[p^{k}])$
.
We next recall Howard’s abstract generalisation of Rubin’s height formula for derived p-adic heights. For every prime v of K above p, let
![]() $\mathscr {F}_{v}^{+}T_{p}E$
be the kernel of the reduction map
$\mathscr {F}_{v}^{+}T_{p}E$
be the kernel of the reduction map
![]() $T_{p}E\rightarrow T_{p}\tilde {E}$
, where
$T_{p}E\rightarrow T_{p}\tilde {E}$
, where
![]() $\tilde {E}$
is the reduction of E modulo v. Letting
$\tilde {E}$
is the reduction of E modulo v. Letting
![]() $V=V_{p}E$
, this induces the filtration
$V=V_{p}E$
, this induces the filtration
![]() $\mathscr {F}_{v}^{+}V\subseteq V$
. For every prime
$\mathscr {F}_{v}^{+}V\subseteq V$
. For every prime
![]() $v\vert p$
of K, write
$v\vert p$
of K, write
 $$ \begin{align*} \widehat{\textrm{H}}^{1}_{\textrm{fin}}(K_{\infty,v},V)=\bigoplus_{w\vert v}\widehat{\textrm{H}}^{1}(K_{\infty,w},\mathscr{F}_{v}^{+}V), \end{align*} $$
$$ \begin{align*} \widehat{\textrm{H}}^{1}_{\textrm{fin}}(K_{\infty,v},V)=\bigoplus_{w\vert v}\widehat{\textrm{H}}^{1}(K_{\infty,w},\mathscr{F}_{v}^{+}V), \end{align*} $$
where w runs over the places of
![]() $K_{\infty }$
above v. The local pairings in (3.6) induce a semi-local pairing
$K_{\infty }$
above v. The local pairings in (3.6) induce a semi-local pairing
 $$ \begin{align*} \langle-,-\rangle_{K_{\infty,v}}:\widehat{\textrm{H}}^{1}(K_{\infty,v},V)\times\widehat{\textrm{H}}^{1}_{\textrm{fin}}(K_{\infty,v},V)\rightarrow\Lambda\otimes_{\mathbf{Z}_{p}}{\mathbf{Q}}_{p} \end{align*} $$
$$ \begin{align*} \langle-,-\rangle_{K_{\infty,v}}:\widehat{\textrm{H}}^{1}(K_{\infty,v},V)\times\widehat{\textrm{H}}^{1}_{\textrm{fin}}(K_{\infty,v},V)\rightarrow\Lambda\otimes_{\mathbf{Z}_{p}}{\mathbf{Q}}_{p} \end{align*} $$
which induces a perfect duality between the
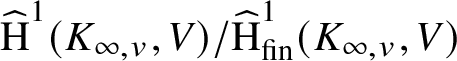 $\widehat {\text {H}}^{1}(K_{\infty ,v},V)/\widehat {\text {H}}^{1}_{\text {fin}}(K_{\infty ,v},V)$
and
$\widehat {\text {H}}^{1}(K_{\infty ,v},V)/\widehat {\text {H}}^{1}_{\text {fin}}(K_{\infty ,v},V)$
and
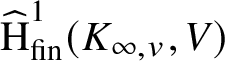 $\widehat {\text {H}}^{1}_{\text {fin}}(K_{\infty ,v},V)$
. Every class
$\widehat {\text {H}}^{1}_{\text {fin}}(K_{\infty ,v},V)$
. Every class
 ${\mathbf z}\in \widehat {\text {H}}^{1}(K_{\infty },V)$
defines a linear map
${\mathbf z}\in \widehat {\text {H}}^{1}(K_{\infty },V)$
defines a linear map
 $$ \begin{align*} \mathcal{L}_{p,{\mathbf z}}=\sum_{v\vert p}\langle\textrm{Loc}_{v}({\mathbf z}),-\rangle_{K_{\infty,v}}:\widehat{\textrm{H}}^{1}_{\textrm{fin}}(K_{\infty,p},V)=\bigoplus_{v\vert p}\widehat{\textrm{H}}^{1}_{\textrm{fin}}(K_{\infty,v},V)\rightarrow\Lambda\otimes_{\mathbf{Z}_{p}}{\mathbf{Q}}_{p}. \end{align*} $$
$$ \begin{align*} \mathcal{L}_{p,{\mathbf z}}=\sum_{v\vert p}\langle\textrm{Loc}_{v}({\mathbf z}),-\rangle_{K_{\infty,v}}:\widehat{\textrm{H}}^{1}_{\textrm{fin}}(K_{\infty,p},V)=\bigoplus_{v\vert p}\widehat{\textrm{H}}^{1}_{\textrm{fin}}(K_{\infty,v},V)\rightarrow\Lambda\otimes_{\mathbf{Z}_{p}}{\mathbf{Q}}_{p}. \end{align*} $$
Let
![]() $\text {ord}(\mathcal {L}_{p,{\mathbf z}})$
be the largest integer r such that the image of
$\text {ord}(\mathcal {L}_{p,{\mathbf z}})$
be the largest integer r such that the image of
![]() $\mathcal {L}_{p,{\mathbf z}}$
is contained in
$\mathcal {L}_{p,{\mathbf z}}$
is contained in
![]() $J^{r}$
.
$J^{r}$
.
Theorem 4.2. Let r be any positive integer with
![]() $r\leqslant \mathrm{ord}(\mathcal {L}_{p,{\mathbf z}})$
. Then
$r\leqslant \mathrm{ord}(\mathcal {L}_{p,{\mathbf z}})$
. Then
![]() $z=\mathrm{pr}_{K}({\mathbf z})$
belongs to
$z=\mathrm{pr}_{K}({\mathbf z})$
belongs to
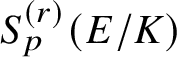 $S_{p}^{(r)}(E/K)$
and for any
$S_{p}^{(r)}(E/K)$
and for any
 $w\in S_{p}^{(r)}(E/K)$
we have
$w\in S_{p}^{(r)}(E/K)$
we have
 $$ \begin{align*} h_{p}^{(r)}(z,w)=- \mathcal{L}_{p,{\mathbf z}}(\mathbf{w}_{p})\pmod{J^{r+1}} \end{align*} $$
$$ \begin{align*} h_{p}^{(r)}(z,w)=- \mathcal{L}_{p,{\mathbf z}}(\mathbf{w}_{p})\pmod{J^{r+1}} \end{align*} $$
where
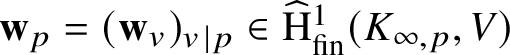 $\mathbf {w}_{p}=(\mathbf {w}_{v})_{v\vert p}\in \widehat {\mathrm{H}}^{1}_{\mathrm{fin}}(K_{\infty ,p},V)$
is any semi-local class with
$\mathbf {w}_{p}=(\mathbf {w}_{v})_{v\vert p}\in \widehat {\mathrm{H}}^{1}_{\mathrm{fin}}(K_{\infty ,p},V)$
is any semi-local class with
![]() $\mathrm{pr}_{K_{v}}({\mathbf w}_{v})=\mathrm{Loc}_{v}(w)$
for all
$\mathrm{pr}_{K_{v}}({\mathbf w}_{v})=\mathrm{Loc}_{v}(w)$
for all
![]() $v\vert p$
.
$v\vert p$
.
Proof. This is a reformulation of part (c) of Theorem 2.5 in [Reference Howard26]. Note that the existence of
![]() ${\mathbf w}_{p}$
follows from the definition of
${\mathbf w}_{p}$
follows from the definition of
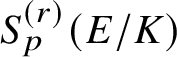 $S_{p}^{(r)}(E/K)$
in [Reference Howard26], and the fact that the image
$S_{p}^{(r)}(E/K)$
in [Reference Howard26], and the fact that the image
![]() $\mathcal {L}_{p,{\mathbf z}}(\mathbf {w}_{p})\in J^{r}/J^{r+1}$
is independent of the choice of
$\mathcal {L}_{p,{\mathbf z}}(\mathbf {w}_{p})\in J^{r}/J^{r+1}$
is independent of the choice of
![]() $\mathbf {w}_{p}$
is shown in the proof.
$\mathbf {w}_{p}$
is shown in the proof.
4.2 Derived p-adic heights and the Coleman map
Now we compute the local expression in Theorem 4.2 for the derived p-adic height pairing in terms of the Coleman map from Section 3, yielding our higher rank generalisation of Rubin’s formula.
We use the setting and notations introduced after Lemma 3.5. In particular,
![]() $(p)={\mathfrak p}\overline {{\mathfrak p}}$
splits in K, with
$(p)={\mathfrak p}\overline {{\mathfrak p}}$
splits in K, with
![]() ${\mathfrak p}$
the prime of K above p induced by our fixed embedding
${\mathfrak p}$
the prime of K above p induced by our fixed embedding
 $\overline {\mathbf {Q}}\hookrightarrow \overline {\mathbf {Q}}_{p}$
. Let
$\overline {\mathbf {Q}}\hookrightarrow \overline {\mathbf {Q}}_{p}$
. Let
![]() $\hat K_{\infty }$
be the closure of the image of
$\hat K_{\infty }$
be the closure of the image of
![]() $K_{\infty }$
in
$K_{\infty }$
in
 $\overline {\mathbf {Q}}_{p}$
under this embedding and put
$\overline {\mathbf {Q}}_{p}$
under this embedding and put
 $$ \begin{align*} \Gamma_{\infty}=\operatorname{\mathrm{Gal}}(K_{\infty}/K),\quad\hat\Gamma_{\infty}=\operatorname{\mathrm{Gal}}(\hat K_{\infty}/{\mathbf{Q}}_{p}), \end{align*} $$
$$ \begin{align*} \Gamma_{\infty}=\operatorname{\mathrm{Gal}}(K_{\infty}/K),\quad\hat\Gamma_{\infty}=\operatorname{\mathrm{Gal}}(\hat K_{\infty}/{\mathbf{Q}}_{p}), \end{align*} $$
so, naturally,
![]() $\hat \Gamma _{\infty }$
is a subgroup of
$\hat \Gamma _{\infty }$
is a subgroup of
![]() $\Gamma _{\infty }$
. Also, we put
$\Gamma _{\infty }$
. Also, we put
![]() $F=\hat {H}_{c}$
for some fixed c prime to p and
$F=\hat {H}_{c}$
for some fixed c prime to p and
![]() $F_{\infty }=\hat {H}_{cp^{\infty }}$
, which is a finite extension of
$F_{\infty }=\hat {H}_{cp^{\infty }}$
, which is a finite extension of
![]() $\hat K_{\infty }$
.
$\hat K_{\infty }$
.
Let
![]() $\boldsymbol {e}\in R^{\psi _{\mathcal F}=0}$
be a generator over
$\boldsymbol {e}\in R^{\psi _{\mathcal F}=0}$
be a generator over
![]() such that
such that
![]() $\boldsymbol {e}(0)=1$
. Define
$\boldsymbol {e}(0)=1$
. Define
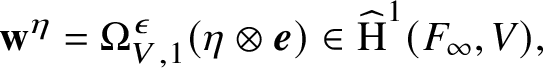 $$ \begin{align}{\mathbf w}^{\eta}=\Omega^{\epsilon}_{V,1}(\eta\otimes \boldsymbol{e})\in \widehat{\textrm{H}}^{1}(F_{\infty},V),\end{align} $$
$$ \begin{align}{\mathbf w}^{\eta}=\Omega^{\epsilon}_{V,1}(\eta\otimes \boldsymbol{e})\in \widehat{\textrm{H}}^{1}(F_{\infty},V),\end{align} $$
where
![]() $\Omega _{V,1}^{\epsilon }$
in is the big exponential map in Theorem 3.2.
$\Omega _{V,1}^{\epsilon }$
in is the big exponential map in Theorem 3.2.
As in Subsection 3.3, we let
![]() $\sigma _{0}\in \operatorname {\mathrm {Gal}}(F_{\infty }^{\text {ur}}/{\mathbf {Q}}_{p})$
be such that
$\sigma _{0}\in \operatorname {\mathrm {Gal}}(F_{\infty }^{\text {ur}}/{\mathbf {Q}}_{p})$
be such that
![]() $\sigma _{0}|_{{\mathbf {Q}}_{p}^{\text {ur}}}=\mathrm {Fr}$
is the absolute Frobenius.
$\sigma _{0}|_{{\mathbf {Q}}_{p}^{\text {ur}}}=\mathrm {Fr}$
is the absolute Frobenius.
Proposition 4.3. Let
 ${\mathbf {Q}}_{p}^{\mathrm{cyc}}$
be the cyclotomic
${\mathbf {Q}}_{p}^{\mathrm{cyc}}$
be the cyclotomic
![]() $\mathbf {Z}_{p}^{\times }$
-extension of
$\mathbf {Z}_{p}^{\times }$
-extension of
![]() ${\mathbf {Q}}_{p}$
. Let
${\mathbf {Q}}_{p}$
. Let
![]() $\sigma _{\mathrm{cyc}}\in \operatorname {\mathrm {Gal}}(F^{\mathrm{ur}}_{\infty }/{\mathbf {Q}}_{p})$
be the Frobenius such that
$\sigma _{\mathrm{cyc}}\in \operatorname {\mathrm {Gal}}(F^{\mathrm{ur}}_{\infty }/{\mathbf {Q}}_{p})$
be the Frobenius such that
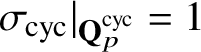 $\sigma _{\mathrm{cyc}}|_{{\mathbf {Q}}_{p}^{\mathrm{cyc}}}=1$
and
$\sigma _{\mathrm{cyc}}|_{{\mathbf {Q}}_{p}^{\mathrm{cyc}}}=1$
and
![]() $\sigma _{\mathrm{cyc}}|_{{\mathbf {Q}}_{p}^{\mathrm{ur}}}=\mathrm {Fr}$
. For each
$\sigma _{\mathrm{cyc}}|_{{\mathbf {Q}}_{p}^{\mathrm{ur}}}=\mathrm {Fr}$
. For each
![]() $\hat {\mathbf z}\in \widehat {\mathrm{H}}^{1}(\hat K_{\infty },V)$
, we have
$\hat {\mathbf z}\in \widehat {\mathrm{H}}^{1}(\hat K_{\infty },V)$
, we have

Proof. We first recall that for every
![]() $e\in (R\otimes _{\mathscr O}{\mathcal W})^{\psi _{\mathcal F}=0}$
, the big exponential map
$e\in (R\otimes _{\mathscr O}{\mathcal W})^{\psi _{\mathcal F}=0}$
, the big exponential map
 $\Omega ^{\epsilon }_{V,1}(\eta \otimes e)$
in Theorem 3.2 is given by
$\Omega ^{\epsilon }_{V,1}(\eta \otimes e)$
in Theorem 3.2 is given by
where
![]() $G_{e}\in {\mathbf D}(V)\otimes {\mathscr H}_{1,\mathcal Q}(X)$
is a solution of
$G_{e}\in {\mathbf D}(V)\otimes {\mathscr H}_{1,\mathcal Q}(X)$
is a solution of
![]() $(1-\varphi \otimes \varphi _{\mathcal F})G_{e}=\eta \otimes e$
and
$(1-\varphi \otimes \varphi _{\mathcal F})G_{e}=\eta \otimes e$
and
![]() $\Xi _{n,V}$
is as in
$\Xi _{n,V}$
is as in
![]() $(3.4)$
. Taking
$(3.4)$
. Taking
 $$ \begin{align*} G_{e}=G_{\boldsymbol{e}}=\sum_{m=0}^{\infty}(\varphi\otimes\varphi_{\mathcal F})^{m}(\eta\otimes\boldsymbol{e})=\sum_{m=0}^{\infty}\varphi^{m}\eta\otimes\boldsymbol{e}^{\textrm{Fr}^{m}},\\[-15pt] \end{align*} $$
$$ \begin{align*} G_{e}=G_{\boldsymbol{e}}=\sum_{m=0}^{\infty}(\varphi\otimes\varphi_{\mathcal F})^{m}(\eta\otimes\boldsymbol{e})=\sum_{m=0}^{\infty}\varphi^{m}\eta\otimes\boldsymbol{e}^{\textrm{Fr}^{m}},\\[-15pt] \end{align*} $$
we obtain
 $$ \begin{align} \begin{aligned}\Xi_{n,V}(G_{\boldsymbol{e}})&=p^{-(n+1)}(\varphi^{-(n+1)}\otimes 1)G_{\boldsymbol{e}}^{\mathrm{Fr}^{-(n+1)}}(\epsilon_{n})\\ &=\sum_{m=0}^{\infty} (p\varphi)^{-(n+1)}\varphi^{m}\eta\otimes \boldsymbol{e}^{\mathrm{Fr}^{m-(n+1)}}(\epsilon_{n-m}). \end{aligned} \\[-15pt]\nonumber\end{align} $$
$$ \begin{align} \begin{aligned}\Xi_{n,V}(G_{\boldsymbol{e}})&=p^{-(n+1)}(\varphi^{-(n+1)}\otimes 1)G_{\boldsymbol{e}}^{\mathrm{Fr}^{-(n+1)}}(\epsilon_{n})\\ &=\sum_{m=0}^{\infty} (p\varphi)^{-(n+1)}\varphi^{m}\eta\otimes \boldsymbol{e}^{\mathrm{Fr}^{m-(n+1)}}(\epsilon_{n-m}). \end{aligned} \\[-15pt]\nonumber\end{align} $$
Put
![]() $z_{n}=\text {pr}_{\hat K_{n}}(\hat {\mathbf z})$
and
$z_{n}=\text {pr}_{\hat K_{n}}(\hat {\mathbf z})$
and
 $\hat G_{n}=\operatorname {\mathrm {Gal}}(\hat {K}_{n}/{\mathbf {Q}}_{p})$
. From the definition of the Coleman map
$\hat G_{n}=\operatorname {\mathrm {Gal}}(\hat {K}_{n}/{\mathbf {Q}}_{p})$
. From the definition of the Coleman map
![]() $\text {Col}_{e}^{\epsilon }$
and using in (4.4) and (4.5), we thus find that
$\text {Col}_{e}^{\epsilon }$
and using in (4.4) and (4.5), we thus find that
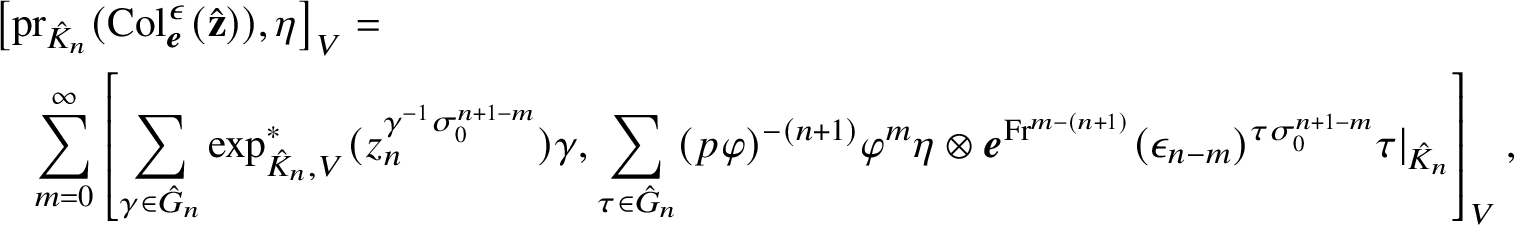 $$ \begin{align} &\left[ \text{pr}_{\hat K_{n}}(\text{Col}^{\epsilon}_{\boldsymbol{e}}(\hat{\mathbf z})), \eta\right]_{V}=\nonumber\\ &\quad\sum_{m=0}^{\infty}\left[ \sum_{\gamma\in \hat G_{n}}\exp^{*}_{\hat K_{n},V}(z_{n}^{\gamma^{-1}\sigma_{0}^{n+1-m}})\gamma, \sum_{\tau\in\hat G_{n}} (p\varphi)^{-(n+1)}\varphi^{m}\eta\otimes\boldsymbol{e}^{\mathrm{Fr}^{m-(n+1)}}(\epsilon_{n-m})^{\tau\sigma_{0}^{n+1-m}}\tau|_{\hat K_{n}}\right]_{V},\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} &\left[ \text{pr}_{\hat K_{n}}(\text{Col}^{\epsilon}_{\boldsymbol{e}}(\hat{\mathbf z})), \eta\right]_{V}=\nonumber\\ &\quad\sum_{m=0}^{\infty}\left[ \sum_{\gamma\in \hat G_{n}}\exp^{*}_{\hat K_{n},V}(z_{n}^{\gamma^{-1}\sigma_{0}^{n+1-m}})\gamma, \sum_{\tau\in\hat G_{n}} (p\varphi)^{-(n+1)}\varphi^{m}\eta\otimes\boldsymbol{e}^{\mathrm{Fr}^{m-(n+1)}}(\epsilon_{n-m})^{\tau\sigma_{0}^{n+1-m}}\tau|_{\hat K_{n}}\right]_{V},\\[-15pt]\nonumber \end{align} $$
where
 $\text {exp}_{\hat K_{n},V}^{*}$
is the Bloch–Kato dual exponential map.
$\text {exp}_{\hat K_{n},V}^{*}$
is the Bloch–Kato dual exponential map.
On the other hand, it is immediately seen that
 $$ \begin{align*} \textrm{pr}_{\hat K_{n}}(\langle \hat{\mathbf z}, \textrm{cor}_{F_{\infty}/\hat K_{\infty}}({\mathbf w}^{\eta})\rangle_{\hat K_{\infty}})=\frac{1}{[F_{\infty}:\hat K_{\infty}]}\sum_{j=1}^{[F:{\mathbf{Q}}_{p}]}\textrm{pr}_{\hat K_{n}}(\langle \hat{\mathbf z}^{\sigma_{0}^{-j}}, {\mathbf w}^{\eta}\rangle_{F_{\infty}})\sigma_{0}^{j}|_{\hat K_{n}},\\[-15pt] \end{align*} $$
$$ \begin{align*} \textrm{pr}_{\hat K_{n}}(\langle \hat{\mathbf z}, \textrm{cor}_{F_{\infty}/\hat K_{\infty}}({\mathbf w}^{\eta})\rangle_{\hat K_{\infty}})=\frac{1}{[F_{\infty}:\hat K_{\infty}]}\sum_{j=1}^{[F:{\mathbf{Q}}_{p}]}\textrm{pr}_{\hat K_{n}}(\langle \hat{\mathbf z}^{\sigma_{0}^{-j}}, {\mathbf w}^{\eta}\rangle_{F_{\infty}})\sigma_{0}^{j}|_{\hat K_{n}},\\[-15pt] \end{align*} $$
and from (4.6) we find that
 $$ \begin{align*} &\text{pr}_{\hat K_{n}}(\langle \hat{\mathbf z}^{\sigma_{0}^{-j}}, {\mathbf w}^{\eta}\rangle_{F_{\infty}})=\sum_{\gamma\in\hat G_{n}}\langle z_{n}^{\sigma_{0}^{-j}\gamma^{-1}}, \exp_{F_{n},V}(\Xi_{n,V}(G_{\boldsymbol{e}})\rangle_{F_{n}}\gamma|_{\hat K_{n}}\\ &=\operatorname{\mathrm{Tr}}_{F_{n}/{\mathbf{Q}}_{p}}\left(\left[ \sum_{\gamma\in\hat G_{n}}\exp^{*}_{\hat K_{n},V}(z_{n}^{\sigma_{0}^{-j}\gamma^{-1}})\gamma|_{\hat K_{\infty}}, \Xi_{n,V}(G_{\boldsymbol{e}})\right]_{V}\right)\\ &=\sum_{m=0}^{\infty}\sum_{i=1}^{[F:{\mathbf{Q}}_{p}]} \left[ \sum_{\gamma\in \hat G_{n}}\exp^{*}_{\hat K_{n},V}(z_{n}^{\gamma^{-1}\sigma_{0}^{i-j+n+1-m}})\gamma, \sum_{\tau\in \hat G_{n}} (p\varphi)^{-(n+1)}\varphi^{m}\eta\otimes \boldsymbol{e}^{\mathrm{Fr}^{m-(n+1)}}(\epsilon_{n-m})^{\tau\sigma_{0}^{i+n+1-m}}\tau|_{\hat K_{n}}\right]\\ &=\sum_{i=1}^{[F:{\mathbf{Q}}_{p}]}\left[ \text{pr}_{\hat K_{n}}(\text{Col}_{\boldsymbol{e}}^{\epsilon}({\mathbf z}^{\sigma_{0}^{-j}})^{\sigma_{0}^{i}}), \eta\right]. \end{align*} $$
$$ \begin{align*} &\text{pr}_{\hat K_{n}}(\langle \hat{\mathbf z}^{\sigma_{0}^{-j}}, {\mathbf w}^{\eta}\rangle_{F_{\infty}})=\sum_{\gamma\in\hat G_{n}}\langle z_{n}^{\sigma_{0}^{-j}\gamma^{-1}}, \exp_{F_{n},V}(\Xi_{n,V}(G_{\boldsymbol{e}})\rangle_{F_{n}}\gamma|_{\hat K_{n}}\\ &=\operatorname{\mathrm{Tr}}_{F_{n}/{\mathbf{Q}}_{p}}\left(\left[ \sum_{\gamma\in\hat G_{n}}\exp^{*}_{\hat K_{n},V}(z_{n}^{\sigma_{0}^{-j}\gamma^{-1}})\gamma|_{\hat K_{\infty}}, \Xi_{n,V}(G_{\boldsymbol{e}})\right]_{V}\right)\\ &=\sum_{m=0}^{\infty}\sum_{i=1}^{[F:{\mathbf{Q}}_{p}]} \left[ \sum_{\gamma\in \hat G_{n}}\exp^{*}_{\hat K_{n},V}(z_{n}^{\gamma^{-1}\sigma_{0}^{i-j+n+1-m}})\gamma, \sum_{\tau\in \hat G_{n}} (p\varphi)^{-(n+1)}\varphi^{m}\eta\otimes \boldsymbol{e}^{\mathrm{Fr}^{m-(n+1)}}(\epsilon_{n-m})^{\tau\sigma_{0}^{i+n+1-m}}\tau|_{\hat K_{n}}\right]\\ &=\sum_{i=1}^{[F:{\mathbf{Q}}_{p}]}\left[ \text{pr}_{\hat K_{n}}(\text{Col}_{\boldsymbol{e}}^{\epsilon}({\mathbf z}^{\sigma_{0}^{-j}})^{\sigma_{0}^{i}}), \eta\right]. \end{align*} $$
Taking the limit over n, we thus arrive at
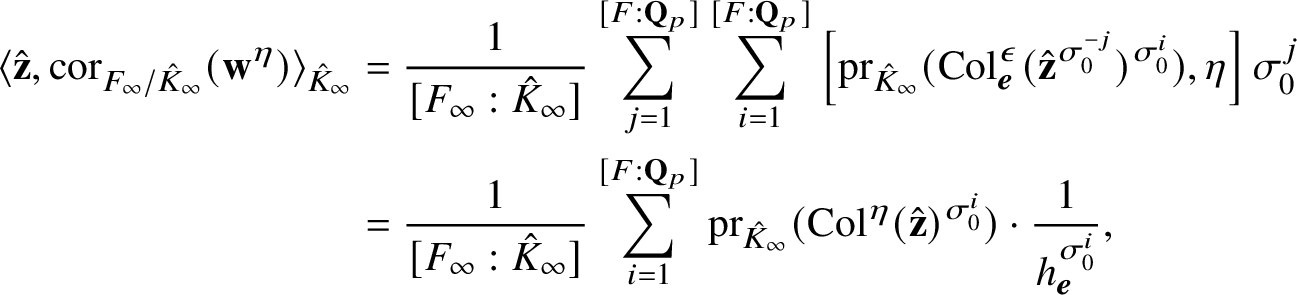 $$ \begin{align} \begin{aligned} \langle \hat{\mathbf z}, \textrm{cor}_{F_{\infty}/\hat K_{\infty}}({\mathbf w}^{\eta})\rangle_{\hat K_{\infty}}&=\frac{1}{[F_{\infty}:\hat K_{\infty}]}\sum_{j=1}^{[F:{\mathbf{Q}}_{p}]}\sum_{i=1}^{[F:{\mathbf{Q}}_{p}]}\left[ \textrm{pr}_{\hat K_{\infty}}(\textrm{Col}_{\boldsymbol{e}}^{\epsilon}(\hat{\mathbf z}^{\sigma_{0}^{-j}})^{\sigma_{0}^{i}}), \eta\right]\sigma_{0}^{j}\\ &=\frac{1}{[F_{\infty}:\hat K_{\infty}]}\sum_{i=1}^{[F:{\mathbf{Q}}_{p}]}\textrm{pr}_{\hat K_{\infty}}(\textrm{Col}^{\eta}(\hat{\mathbf z})^{\sigma_{0}^{i}})\cdot \frac{1}{h_{\boldsymbol{e}}^{\sigma_{0}^{i}}}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \langle \hat{\mathbf z}, \textrm{cor}_{F_{\infty}/\hat K_{\infty}}({\mathbf w}^{\eta})\rangle_{\hat K_{\infty}}&=\frac{1}{[F_{\infty}:\hat K_{\infty}]}\sum_{j=1}^{[F:{\mathbf{Q}}_{p}]}\sum_{i=1}^{[F:{\mathbf{Q}}_{p}]}\left[ \textrm{pr}_{\hat K_{\infty}}(\textrm{Col}_{\boldsymbol{e}}^{\epsilon}(\hat{\mathbf z}^{\sigma_{0}^{-j}})^{\sigma_{0}^{i}}), \eta\right]\sigma_{0}^{j}\\ &=\frac{1}{[F_{\infty}:\hat K_{\infty}]}\sum_{i=1}^{[F:{\mathbf{Q}}_{p}]}\textrm{pr}_{\hat K_{\infty}}(\textrm{Col}^{\eta}(\hat{\mathbf z})^{\sigma_{0}^{i}})\cdot \frac{1}{h_{\boldsymbol{e}}^{\sigma_{0}^{i}}}, \end{aligned} \end{align} $$
using (3.9) for the second equality. Finally, writing
![]() $g_{\rho }=\rho (1+X)$
for the isomorphism
$g_{\rho }=\rho (1+X)$
for the isomorphism
![]() $\rho $
in (3.8), one has
$\rho $
in (3.8), one has
 $g_{\rho }^{\sigma _{0}^{-i}}(\epsilon _{i-1})=\zeta _{p^{i}}\in {\mathbf {Q}}_{p}^{\text {cyc}}$
, which immediately implies the relation
$g_{\rho }^{\sigma _{0}^{-i}}(\epsilon _{i-1})=\zeta _{p^{i}}\in {\mathbf {Q}}_{p}^{\text {cyc}}$
, which immediately implies the relation
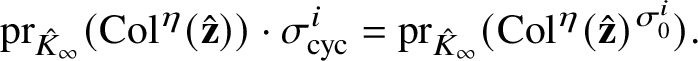 $$ \begin{align*} \textrm{pr}_{\hat K_{\infty}}(\textrm{Col}^{\eta}(\hat{\mathbf z}))\cdot\sigma_{\textrm{cyc}}^{i} =\textrm{pr}_{\hat K_{\infty}}(\textrm{Col}^{\eta}(\hat{\mathbf z})^{\sigma_{0}^{i}}). \end{align*} $$
$$ \begin{align*} \textrm{pr}_{\hat K_{\infty}}(\textrm{Col}^{\eta}(\hat{\mathbf z}))\cdot\sigma_{\textrm{cyc}}^{i} =\textrm{pr}_{\hat K_{\infty}}(\textrm{Col}^{\eta}(\hat{\mathbf z})^{\sigma_{0}^{i}}). \end{align*} $$
Together with (4.7), this concludes the proof.
We shall also need the following result.
Lemma 4.4. The projection of
![]() ${\mathbf w}^{\eta }$
to
${\mathbf w}^{\eta }$
to
![]() $\mathrm{H}^{1}(F,V)$
is given by
$\mathrm{H}^{1}(F,V)$
is given by
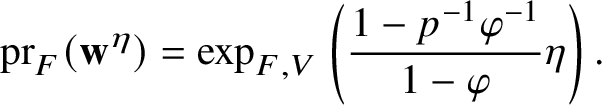 $$ \begin{align*}\mathrm{pr}_{F}({\mathbf w}^{\eta})=\exp_{F,V}\left(\frac{1-p^{-1}\varphi^{-1}}{1-\varphi}\eta\right). \end{align*} $$
$$ \begin{align*}\mathrm{pr}_{F}({\mathbf w}^{\eta})=\exp_{F,V}\left(\frac{1-p^{-1}\varphi^{-1}}{1-\varphi}\eta\right). \end{align*} $$
Proof. Let
![]() $g=\eta \otimes \boldsymbol {e}$
and let
$g=\eta \otimes \boldsymbol {e}$
and let
![]() $G(X)\in {\mathbf D}(V)\otimes {\mathscr H}_{1,\mathcal Q}(X)$
such that
$G(X)\in {\mathbf D}(V)\otimes {\mathscr H}_{1,\mathcal Q}(X)$
such that
![]() $(1-\varphi \otimes \varphi _{\mathcal F})G=g$
. Then
$(1-\varphi \otimes \varphi _{\mathcal F})G=g$
. Then
and, by definition,
where
![]() $\Xi _{0,V}(G)$
is as in
$\Xi _{0,V}(G)$
is as in
![]() $(3.4)$
. Equation (3.1) and the fact that
$(3.4)$
. Equation (3.1) and the fact that
![]() $\psi _{\mathcal F}\boldsymbol {e}(X)=0$
imply that
$\psi _{\mathcal F}\boldsymbol {e}(X)=0$
imply that
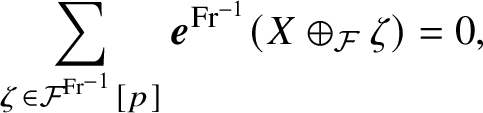 $$ \begin{align*}\sum_{\zeta\in {\mathcal F}^{\mathrm{Fr}^{-1}}[p]}\boldsymbol{e}^{\mathrm{Fr}^{-1}}(X\oplus_{\mathcal F} \zeta)=0,\end{align*} $$
$$ \begin{align*}\sum_{\zeta\in {\mathcal F}^{\mathrm{Fr}^{-1}}[p]}\boldsymbol{e}^{\mathrm{Fr}^{-1}}(X\oplus_{\mathcal F} \zeta)=0,\end{align*} $$
from which we obtain
 $$ \begin{align*}\operatorname{\mathrm{Tr}}_{F_{0}/F}(G^{\mathrm{Fr}^{-1}}(\epsilon_{0}))=\sum_{\tau\in\operatorname{\mathrm{Gal}}(F_{0}/F)}\eta\otimes \boldsymbol{e}(\epsilon_{0}^{\tau})-\eta+(1-\varphi)^{-1}\eta=\frac{p\varphi-1}{1-\varphi}\eta.\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Tr}}_{F_{0}/F}(G^{\mathrm{Fr}^{-1}}(\epsilon_{0}))=\sum_{\tau\in\operatorname{\mathrm{Gal}}(F_{0}/F)}\eta\otimes \boldsymbol{e}(\epsilon_{0}^{\tau})-\eta+(1-\varphi)^{-1}\eta=\frac{p\varphi-1}{1-\varphi}\eta.\end{align*} $$
Together with (4.8), we thus see that
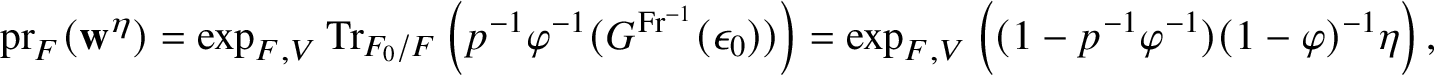 $$ \begin{align*} \text{pr}_{F}({\mathbf w}^{\eta}) &=\exp_{F,V}\operatorname{\mathrm{Tr}}_{F_{0}/F}\left(p^{-1}\varphi^{-1}(G^{\mathrm{Fr}^{-1}}(\epsilon_{0}))\right)=\exp_{F,V}\left((1-p^{-1}\varphi^{-1})(1-\varphi)^{-1} \eta\right), \end{align*} $$
$$ \begin{align*} \text{pr}_{F}({\mathbf w}^{\eta}) &=\exp_{F,V}\operatorname{\mathrm{Tr}}_{F_{0}/F}\left(p^{-1}\varphi^{-1}(G^{\mathrm{Fr}^{-1}}(\epsilon_{0}))\right)=\exp_{F,V}\left((1-p^{-1}\varphi^{-1})(1-\varphi)^{-1} \eta\right), \end{align*} $$
concluding the proof.
Recall the identification
![]() $K_{\mathfrak p}={\mathbf {Q}}_{p}$
and let
$K_{\mathfrak p}={\mathbf {Q}}_{p}$
and let
 $\text {H}^{1}_{\text {fin}}({\mathbf {Q}}_{p},V)\subset \text {H}^{1}({\mathbf {Q}}_{p},V)$
be the subspace given by
$\text {H}^{1}_{\text {fin}}({\mathbf {Q}}_{p},V)\subset \text {H}^{1}({\mathbf {Q}}_{p},V)$
be the subspace given by
 $\text {H}^{1}({\mathbf {Q}}_{p},\mathscr {F}_{\mathfrak p}^{+}V)$
. As is well-known,
$\text {H}^{1}({\mathbf {Q}}_{p},\mathscr {F}_{\mathfrak p}^{+}V)$
. As is well-known,
 $\text {H}^{1}_{\text {fin}}({\mathbf {Q}}_{p},V)$
agrees with the Bloch–Kato finite subspace. Let
$\text {H}^{1}_{\text {fin}}({\mathbf {Q}}_{p},V)$
agrees with the Bloch–Kato finite subspace. Let
 $\text {log}_{\mathbf {Q},V}:\text {H}^{1}_{\text {fin}}({\mathbf {Q}}_{p},V)\rightarrow {\mathbf D}(V)$
be the Bloch–Kato logarithm map and denote by
$\text {log}_{\mathbf {Q},V}:\text {H}^{1}_{\text {fin}}({\mathbf {Q}}_{p},V)\rightarrow {\mathbf D}(V)$
be the Bloch–Kato logarithm map and denote by
![]() $\text {log}_{\omega _{E},{\mathfrak p}}$
the composition
$\text {log}_{\omega _{E},{\mathfrak p}}$
the composition
 $$ \begin{align} \textrm{log}_{\omega,{\mathfrak p}}:\textrm{H}^{1}({\mathbf{Q}}_{p},V)\xrightarrow{\textrm{log}_{\mathbf{Q},V}}{\mathbf D}(V)\xrightarrow{\langle-,\omega_{E}\otimes t^{-1}\rangle_{\textrm{dR}}}{\mathbf{Q}}_{p}. \end{align} $$
$$ \begin{align} \textrm{log}_{\omega,{\mathfrak p}}:\textrm{H}^{1}({\mathbf{Q}}_{p},V)\xrightarrow{\textrm{log}_{\mathbf{Q},V}}{\mathbf D}(V)\xrightarrow{\langle-,\omega_{E}\otimes t^{-1}\rangle_{\textrm{dR}}}{\mathbf{Q}}_{p}. \end{align} $$
For a global class
 ${\mathbf z}\in \widehat {\text {H}}^{1}(K_{\infty },V)$
, put
${\mathbf z}\in \widehat {\text {H}}^{1}(K_{\infty },V)$
, put
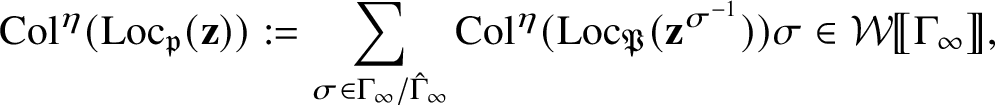
where
 $\text {Loc}_{{\mathfrak P}}:\widehat {\text {H}}^{1}(K_{\infty },V)\rightarrow \widehat {\text {H}}^{1}(\hat {K}_{\infty },V)$
is the restriction map, and let J be the augmentation ideal of
$\text {Loc}_{{\mathfrak P}}:\widehat {\text {H}}^{1}(K_{\infty },V)\rightarrow \widehat {\text {H}}^{1}(\hat {K}_{\infty },V)$
is the restriction map, and let J be the augmentation ideal of
![]() .
.
Theorem 4.5. Let
![]() ${\mathbf z}\in \widehat {\mathrm{H}}^{1}(K_{\infty },V)$
and denote by
${\mathbf z}\in \widehat {\mathrm{H}}^{1}(K_{\infty },V)$
and denote by
![]() $\mathfrak {r}$
be the largest integer r such that
$\mathfrak {r}$
be the largest integer r such that
where
![]() $\overline {{\mathbf z}}={\mathbf z}^{\tau }$
for the complex conjugation
$\overline {{\mathbf z}}={\mathbf z}^{\tau }$
for the complex conjugation
![]() $\tau \in \mathrm {Gal}(K/\mathbf {Q})$
. Then for every
$\tau \in \mathrm {Gal}(K/\mathbf {Q})$
. Then for every
![]() $0<r\leqslant \mathfrak {r}$
, the class
$0<r\leqslant \mathfrak {r}$
, the class
![]() $z=\mathrm{pr}_{K}({\mathbf z})$
belongs to
$z=\mathrm{pr}_{K}({\mathbf z})$
belongs to
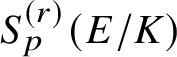 $ S_{p}^{(r)}(E/K)$
, and for every
$ S_{p}^{(r)}(E/K)$
, and for every
 $x\in S_{p}^{(r)}(E/K)$
we have
$x\in S_{p}^{(r)}(E/K)$
we have
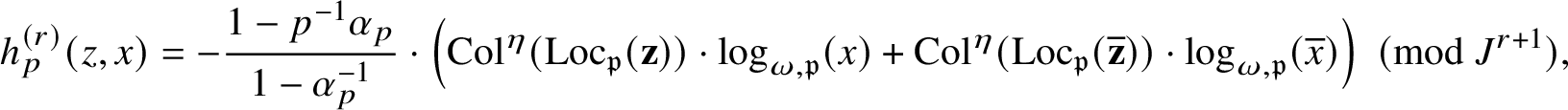 $$ \begin{align*} h_{p}^{(r)}(z,x)&=-\frac{1-p^{-1}\alpha_{p}}{1-\alpha_{p}^{-1}}\cdot \left(\mathrm{Col}^{\eta}(\mathrm{Loc}_{\mathfrak p}({\mathbf z}))\cdot\log_{\omega,\mathfrak{p}}(x)+\mathrm{Col}^{\eta}(\mathrm{Loc}_{\mathfrak p}(\overline{{\mathbf z}}))\cdot\log_{\omega,\mathfrak{p}}(\overline{x})\right)\;(\mathrm{mod}\;{J^{r+1}}), \end{align*} $$
$$ \begin{align*} h_{p}^{(r)}(z,x)&=-\frac{1-p^{-1}\alpha_{p}}{1-\alpha_{p}^{-1}}\cdot \left(\mathrm{Col}^{\eta}(\mathrm{Loc}_{\mathfrak p}({\mathbf z}))\cdot\log_{\omega,\mathfrak{p}}(x)+\mathrm{Col}^{\eta}(\mathrm{Loc}_{\mathfrak p}(\overline{{\mathbf z}}))\cdot\log_{\omega,\mathfrak{p}}(\overline{x})\right)\;(\mathrm{mod}\;{J^{r+1}}), \end{align*} $$
where
![]() $\overline {x}=x^{\tau }$
.
$\overline {x}=x^{\tau }$
.
Proof. The inclusion
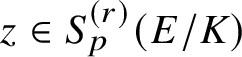 $z\in S_{p}^{(r)}(E/K)$
follows immediately from Theorem 4.2. Let
$z\in S_{p}^{(r)}(E/K)$
follows immediately from Theorem 4.2. Let
 $x\in S_{p}^{(r)}(E/K)$
and put
$x\in S_{p}^{(r)}(E/K)$
and put
 $$ \begin{align*} {\mathbf w}_{{\mathfrak P}}:=\textrm{cor}_{F_{\infty}/\hat K_{\infty}}({\mathbf w}^{\eta})\in \widehat{\textrm{H}}^{1}_{\textrm{fin}}(\hat K_{\infty},V). \end{align*} $$
$$ \begin{align*} {\mathbf w}_{{\mathfrak P}}:=\textrm{cor}_{F_{\infty}/\hat K_{\infty}}({\mathbf w}^{\eta})\in \widehat{\textrm{H}}^{1}_{\textrm{fin}}(\hat K_{\infty},V). \end{align*} $$
Then, since
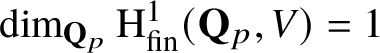 $\dim _{{\mathbf {Q}}_{p}}\text {H}^{1}_{\text {fin}}({\mathbf {Q}}_{p},V)=1$
, we can write
$\dim _{{\mathbf {Q}}_{p}}\text {H}^{1}_{\text {fin}}({\mathbf {Q}}_{p},V)=1$
, we can write
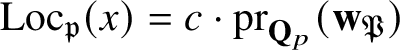 $$ \begin{align*}\textrm{Loc}_{\mathfrak p}(x)=c\cdot \textrm{pr}_{{\mathbf{Q}}_{p}}({\mathbf w}_{\mathfrak P}) \end{align*} $$
$$ \begin{align*}\textrm{Loc}_{\mathfrak p}(x)=c\cdot \textrm{pr}_{{\mathbf{Q}}_{p}}({\mathbf w}_{\mathfrak P}) \end{align*} $$
for some
![]() $c\in {\mathbf {Q}}_{p}$
. Since
$c\in {\mathbf {Q}}_{p}$
. Since
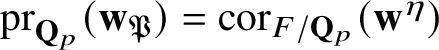 $\text {pr}_{{\mathbf {Q}}_{p}}({\mathbf w}_{{\mathfrak P}})=\text {cor}_{F/{\mathbf {Q}}_{p}}({\mathbf w}^{\eta })$
, from Lemma 4.4 and (3.14) we see that
$\text {pr}_{{\mathbf {Q}}_{p}}({\mathbf w}_{{\mathfrak P}})=\text {cor}_{F/{\mathbf {Q}}_{p}}({\mathbf w}^{\eta })$
, from Lemma 4.4 and (3.14) we see that
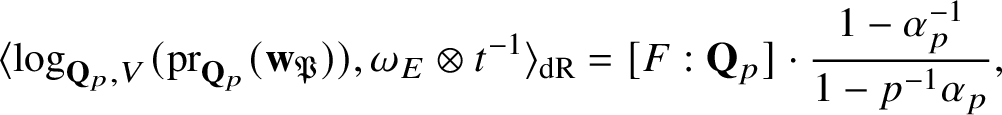 $$ \begin{align*}\langle \log_{{\mathbf{Q}}_{p},V}(\textrm{pr}_{{\mathbf{Q}}_{p}}({\mathbf w}_{{\mathfrak P}})), \omega_{E}\otimes t^{-1}\rangle_{\textrm{dR}}=[F:{\mathbf{Q}}_{p}]\cdot\frac{1-\alpha_{p}^{-1}}{1-p^{-1}\alpha_{p}}, \end{align*} $$
$$ \begin{align*}\langle \log_{{\mathbf{Q}}_{p},V}(\textrm{pr}_{{\mathbf{Q}}_{p}}({\mathbf w}_{{\mathfrak P}})), \omega_{E}\otimes t^{-1}\rangle_{\textrm{dR}}=[F:{\mathbf{Q}}_{p}]\cdot\frac{1-\alpha_{p}^{-1}}{1-p^{-1}\alpha_{p}}, \end{align*} $$
from which we deduce that
 $$ \begin{align*} c=\frac{1-p^{-1}\alpha_{p}}{1-\alpha_{p}^{-1}}\cdot [F:{\mathbf{Q}}_{p}]^{-1}\cdot\log_{\omega_{E},{\mathfrak p}}(x). \end{align*} $$
$$ \begin{align*} c=\frac{1-p^{-1}\alpha_{p}}{1-\alpha_{p}^{-1}}\cdot [F:{\mathbf{Q}}_{p}]^{-1}\cdot\log_{\omega_{E},{\mathfrak p}}(x). \end{align*} $$
Together with the formula in Theorem 4.2, this gives the equality
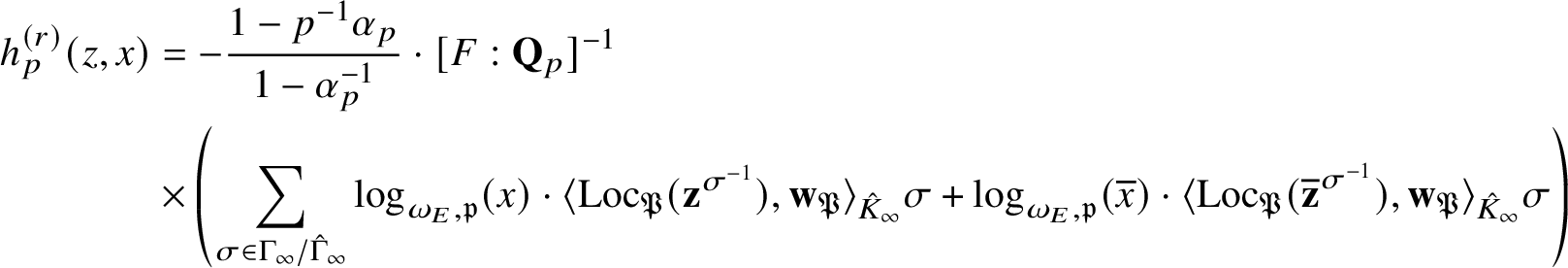 $$ \begin{align*} h_{p}^{(r)}(z,x)&=-\frac{1-p^{-1}\alpha_{p}}{1-\alpha_{p}^{-1}}\cdot[F:{\mathbf{Q}}_{p}]^{-1}\\ &\times\left(\sum_{\sigma\in\Gamma_{\infty}/\hat \Gamma_{\infty}}\log_{\omega_{E},{\mathfrak p}}(x)\cdot\langle \text{Loc}_{{\mathfrak P}}({\mathbf z}^{\sigma^{-1}}), {\mathbf w}_{{\mathfrak P}}\rangle_{\hat K_{\infty}}\sigma+ \log_{\omega_{E},{\mathfrak p}}(\overline{x})\cdot\langle \text{Loc}_{{\mathfrak P}}(\overline{{\mathbf z}}^{\sigma^{-1}}), {\mathbf w}_{{\mathfrak P}}\rangle_{\hat K_{\infty}}\sigma \right) \end{align*} $$
$$ \begin{align*} h_{p}^{(r)}(z,x)&=-\frac{1-p^{-1}\alpha_{p}}{1-\alpha_{p}^{-1}}\cdot[F:{\mathbf{Q}}_{p}]^{-1}\\ &\times\left(\sum_{\sigma\in\Gamma_{\infty}/\hat \Gamma_{\infty}}\log_{\omega_{E},{\mathfrak p}}(x)\cdot\langle \text{Loc}_{{\mathfrak P}}({\mathbf z}^{\sigma^{-1}}), {\mathbf w}_{{\mathfrak P}}\rangle_{\hat K_{\infty}}\sigma+ \log_{\omega_{E},{\mathfrak p}}(\overline{x})\cdot\langle \text{Loc}_{{\mathfrak P}}(\overline{{\mathbf z}}^{\sigma^{-1}}), {\mathbf w}_{{\mathfrak P}}\rangle_{\hat K_{\infty}}\sigma \right) \end{align*} $$
in
![]() $J^{r}/J^{r+1}$
. Since
$J^{r}/J^{r+1}$
. Since
![]() $h_{\boldsymbol {e}}\equiv 1\pmod {J}$
, as is immediate from the defining relation
$h_{\boldsymbol {e}}\equiv 1\pmod {J}$
, as is immediate from the defining relation
![]() $\rho (1+X)=h_{\boldsymbol {e}}\cdot \boldsymbol {e}$
and the fact that
$\rho (1+X)=h_{\boldsymbol {e}}\cdot \boldsymbol {e}$
and the fact that
![]() $\boldsymbol {e}(0)=1$
, the result now follows from Proposition 4.3.
$\boldsymbol {e}(0)=1$
, the result now follows from Proposition 4.3.
5 Proof of the main results
We begin by recalling the setting of Theorem A in the Introduction. Let
![]() $E/\mathbf {Q}$
be an elliptic curve of conductor N with good ordinary reduction at the prime
$E/\mathbf {Q}$
be an elliptic curve of conductor N with good ordinary reduction at the prime
![]() $p>3$
and assume that E has root number
$p>3$
and assume that E has root number
![]() $+1$
and
$+1$
and
![]() $L(E,1)=0$
(so, of course,
$L(E,1)=0$
(so, of course,
![]() $\text {ord}_{s=1}L(E,s)\geqslant 2$
). Let K be an imaginary quadratic field of discriminant prime to N in which
$\text {ord}_{s=1}L(E,s)\geqslant 2$
). Let K be an imaginary quadratic field of discriminant prime to N in which
![]() $(p)=\frak {p}\overline {\frak {p}}$
splits, with
$(p)=\frak {p}\overline {\frak {p}}$
splits, with
![]() $\mathfrak {p}$
the prime of K above p induced by our fixed embedding
$\mathfrak {p}$
the prime of K above p induced by our fixed embedding
 $\overline {\mathbf {Q}}\hookrightarrow \overline {\mathbf {Q}}_{p}$
. Let
$\overline {\mathbf {Q}}\hookrightarrow \overline {\mathbf {Q}}_{p}$
. Let
![]() $\psi $
be a ray class character of K of conductor prime to
$\psi $
be a ray class character of K of conductor prime to
![]() $Np$
and, as in Conjecture 1.2, assume that
$Np$
and, as in Conjecture 1.2, assume that
-
(a)
 $L(E^{K},1)\cdot L(E/K,\chi ,1)\neq 0$
,
$L(E^{K},1)\cdot L(E/K,\chi ,1)\neq 0$
, -
(b)
 $\chi (\overline {\mathfrak {p}})\neq 1$
,
$\chi (\overline {\mathfrak {p}})\neq 1$
,
where
![]() $\chi =\psi /\psi ^{\tau }$
. In addition, we assume that
$\chi =\psi /\psi ^{\tau }$
. In addition, we assume that
-
(c)
 $E[p]$
is irreducible as a
$E[p]$
is irreducible as a
 $G_{\mathbf {Q}}$
-module,
$G_{\mathbf {Q}}$
-module, -
(d)
 $N^{-}$
is the squarefree product of an odd number of primes,
$N^{-}$
is the squarefree product of an odd number of primes, -
(e)
 $E[p]$
is ramified at every prime
$E[p]$
is ramified at every prime
 $q\vert N^{-}$
,
$q\vert N^{-}$
,
where
![]() $N^{-}$
is the maximal factor of N divisible only by primes inert in K. Let
$N^{-}$
is the maximal factor of N divisible only by primes inert in K. Let
![]() $(f,g,g^{*})$
be the triple consisting of the newform
$(f,g,g^{*})$
be the triple consisting of the newform
![]() $f\in S_{2}(\Gamma _{0}(N))$
associated to E and the weight 1 theta series associated to
$f\in S_{2}(\Gamma _{0}(N))$
associated to E and the weight 1 theta series associated to
![]() $\psi $
and
$\psi $
and
![]() $\psi ^{-1}$
, respectively. Finally, put
$\psi ^{-1}$
, respectively. Finally, put
![]() $\alpha =\psi (\overline {{\mathfrak p}})$
and
$\alpha =\psi (\overline {{\mathfrak p}})$
and
![]() $\beta =\psi ({\mathfrak p})$
.
$\beta =\psi ({\mathfrak p})$
.
5.1 Generalised Kato classes
By construction, the Hida families

considered in Subsection 2.4 specialise at
![]() $S=\mathbf {v}-1$
to
$S=\mathbf {v}-1$
to
![]() $g_{\alpha }$
and
$g_{\alpha }$
and
![]() $g_{\alpha ^{-1}}^{*}$
, the p-stabilisations of g and
$g_{\alpha ^{-1}}^{*}$
, the p-stabilisations of g and
![]() $g^{*}$
with
$g^{*}$
with
![]() $U_{p}$
-eigenvalue
$U_{p}$
-eigenvalue
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha ^{-1}$
, respectively. Thus, for every choice of test vectors
$\alpha ^{-1}$
, respectively. Thus, for every choice of test vectors
 $(\breve f,\breve {{\boldsymbol {g}}}_{\alpha },\breve {{\boldsymbol {g}}}^{*}_{\alpha ^{-1}})$
the
$(\breve f,\breve {{\boldsymbol {g}}}_{\alpha },\breve {{\boldsymbol {g}}}^{*}_{\alpha ^{-1}})$
the
-adic class
 $\kappa (\breve f,\breve {{\boldsymbol {g}}}_{\alpha }\breve {{\boldsymbol {g}}}^{*}_{\alpha ^{-1}})$
in
$\kappa (\breve f,\breve {{\boldsymbol {g}}}_{\alpha }\breve {{\boldsymbol {g}}}^{*}_{\alpha ^{-1}})$
in
![]() $(3.11)$
specialises to the generalised Kato class
$(3.11)$
specialises to the generalised Kato class
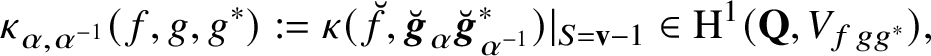 $$ \begin{align*} \kappa_{\alpha,\alpha^{-1}}(f,g,g^{*}):=\kappa(\breve{f},{\breve{{\boldsymbol{g}}}_{\alpha}\breve{{\boldsymbol{g}}}}^{*}_{\alpha^{-1}})\vert_{S=\mathbf{v}-1}\in \textrm{H}^{1}(\mathbf{Q},V_{fgg^{*}}),\nonumber \end{align*} $$
$$ \begin{align*} \kappa_{\alpha,\alpha^{-1}}(f,g,g^{*}):=\kappa(\breve{f},{\breve{{\boldsymbol{g}}}_{\alpha}\breve{{\boldsymbol{g}}}}^{*}_{\alpha^{-1}})\vert_{S=\mathbf{v}-1}\in \textrm{H}^{1}(\mathbf{Q},V_{fgg^{*}}),\nonumber \end{align*} $$
where
![]() $V_{fgg^{*}}:=V_{f}\otimes V_{g}\otimes V_{g^{*}}$
.
$V_{fgg^{*}}:=V_{f}\otimes V_{g}\otimes V_{g^{*}}$
.
Varying over the possible combinations of roots of the Hecke polynomial at p for g and
![]() $g^{*}$
, we thus obtain the four generalised Kato classes
$g^{*}$
, we thus obtain the four generalised Kato classes
 $$ \begin{align} \kappa_{\alpha,\alpha^{-1}}(f,g,g^{*}),\;\kappa_{\alpha,\beta^{-1}}(f,g,g^{*}),\;\kappa_{\beta,\alpha^{-1}}(f,g,g^{*}),\;\kappa_{\beta,\beta^{-1}}(f,g,g^{*})\in\textrm{H}^{1}(\mathbf{Q},V_{fgg^{*}}). \end{align} $$
$$ \begin{align} \kappa_{\alpha,\alpha^{-1}}(f,g,g^{*}),\;\kappa_{\alpha,\beta^{-1}}(f,g,g^{*}),\;\kappa_{\beta,\alpha^{-1}}(f,g,g^{*}),\;\kappa_{\beta,\beta^{-1}}(f,g,g^{*})\in\textrm{H}^{1}(\mathbf{Q},V_{fgg^{*}}). \end{align} $$
Note the
![]() $G_{\mathbf {Q}}$
-module decomposition (1.7) yields
$G_{\mathbf {Q}}$
-module decomposition (1.7) yields
 $$ \begin{align*} \text{H}^{1}(\mathbf{Q},V_{fgg^{*}})&\simeq\text{H}^{1}(\mathbf{Q},V_{p}E)\oplus\text{H}^{1}(\mathbf{Q},V_{p}E\otimes\text{ad}^{0}V_{p}(g))\\ &\simeq\text{H}^{1}(\mathbf{Q},V_{p}E)\oplus\text{H}^{1}(\mathbf{Q},V_{p}E^{K})\oplus\text{H}^{1}(K,V_{p}E\otimes\chi), \end{align*} $$
$$ \begin{align*} \text{H}^{1}(\mathbf{Q},V_{fgg^{*}})&\simeq\text{H}^{1}(\mathbf{Q},V_{p}E)\oplus\text{H}^{1}(\mathbf{Q},V_{p}E\otimes\text{ad}^{0}V_{p}(g))\\ &\simeq\text{H}^{1}(\mathbf{Q},V_{p}E)\oplus\text{H}^{1}(\mathbf{Q},V_{p}E^{K})\oplus\text{H}^{1}(K,V_{p}E\otimes\chi), \end{align*} $$
where
![]() $E^{K}$
is the twist of E by the quadratic character corresponding to K.
$E^{K}$
is the twist of E by the quadratic character corresponding to K.
Lemma 5.1. The projections to
![]() $\mathrm{H}^{1}(\mathbf {Q},V_{p}E)$
of each of the classes in
$\mathrm{H}^{1}(\mathbf {Q},V_{p}E)$
of each of the classes in
![]() $(5.1)$
lands in
$(5.1)$
lands in
![]() $\mathrm{Sel}(\mathbf {Q},V_{p}E)$
.
$\mathrm{Sel}(\mathbf {Q},V_{p}E)$
.
Proof. Since we are assuming
![]() $L(E,1)=0$
and (a) above, the result follows from the vanishing of
$L(E,1)=0$
and (a) above, the result follows from the vanishing of
![]() $\text {Sel}(\mathbf {Q},V_{p}E^{K})$
and
$\text {Sel}(\mathbf {Q},V_{p}E^{K})$
and
![]() $\text {Sel}(K,V_{p}E\otimes \chi )$
by the same argument as in Lemma 3.5.
$\text {Sel}(K,V_{p}E\otimes \chi )$
by the same argument as in Lemma 3.5.
5.2 Vanishing of
 $\kappa _{\alpha ,\beta ^{-1}}(f,g,g^{*})$
and
$\kappa _{\alpha ,\beta ^{-1}}(f,g,g^{*})$
and
 $\kappa _{\beta ,\alpha ^{-1}}(f,g,g^{*})$
$\kappa _{\beta ,\alpha ^{-1}}(f,g,g^{*})$
This part follows easily from the work of Darmon–Rotger [Reference Darmon and Rotger19] and Bertolini–Seveso–Venerucci [Reference Bertolini, Seveso and Venerucci1].
Proposition 5.2.
![]() $\kappa _{\alpha ,\beta ^{-1}}(f,g,g^{*})=\kappa _{\beta ,\alpha ^{-1}}(f,g,g^{*})=0$
.
$\kappa _{\alpha ,\beta ^{-1}}(f,g,g^{*})=\kappa _{\beta ,\alpha ^{-1}}(f,g,g^{*})=0$
.
Proof. Let
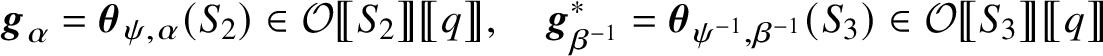
be CM Hida families as in Subsection 2.4 but passing through the specialisation
![]() $(g_{\alpha },g_{\beta ^{-1}})$
rather than
$(g_{\alpha },g_{\beta ^{-1}})$
rather than
![]() $(g_{\alpha },g_{\alpha ^{-1}})$
. Let
$(g_{\alpha },g_{\alpha ^{-1}})$
. Let
 $$ \begin{align} \kappa(f,{\boldsymbol{g}}_{\alpha}{\boldsymbol{g}}_{\beta^{-1}}^{*})(S_{2},S_{3})\in\textrm{H}^{1}(\mathbf{Q}, \mathbb{V}^{\dagger}_{f{\boldsymbol{g}}_\alpha{\boldsymbol{g}}^{*}_{\beta^{-1}}}) \end{align} $$
$$ \begin{align} \kappa(f,{\boldsymbol{g}}_{\alpha}{\boldsymbol{g}}_{\beta^{-1}}^{*})(S_{2},S_{3})\in\textrm{H}^{1}(\mathbf{Q}, \mathbb{V}^{\dagger}_{f{\boldsymbol{g}}_\alpha{\boldsymbol{g}}^{*}_{\beta^{-1}}}) \end{align} $$
be the two-variable restriction of the three-variable cohomology class constructed in [Reference Darmon and Rotger19] and [Reference Bertolini, Seveso and Venerucci1] (after a choice of test vectors
![]() $\breve {{\boldsymbol {g}}}_{\alpha }$
,
$\breve {{\boldsymbol {g}}}_{\alpha }$
,
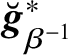 $\breve {{\boldsymbol {g}}}^{*}_{\beta ^{-1}}$
that we omit from the notation), and consider the further restriction
$\breve {{\boldsymbol {g}}}^{*}_{\beta ^{-1}}$
that we omit from the notation), and consider the further restriction
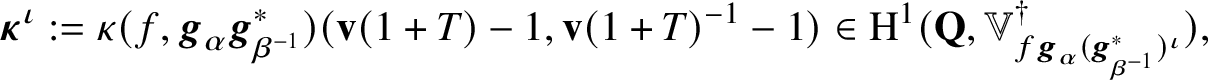 $$ \begin{align*} {\boldsymbol \kappa}^{\iota}:=\kappa(f,{\boldsymbol{g}}_{\alpha}{\boldsymbol{g}}_{\beta^{-1}}^{*})(\mathbf v(1+T)-1,\mathbf v(1+T)^{-1}-1)\in\textrm{H}^{1}(\mathbf{Q},\mathbb{V}^{\dagger}_{f{\boldsymbol{g}}_{\alpha}({\boldsymbol{g}}^{*}_{\beta^{-1}})^{\iota}}), \end{align*} $$
$$ \begin{align*} {\boldsymbol \kappa}^{\iota}:=\kappa(f,{\boldsymbol{g}}_{\alpha}{\boldsymbol{g}}_{\beta^{-1}}^{*})(\mathbf v(1+T)-1,\mathbf v(1+T)^{-1}-1)\in\textrm{H}^{1}(\mathbf{Q},\mathbb{V}^{\dagger}_{f{\boldsymbol{g}}_{\alpha}({\boldsymbol{g}}^{*}_{\beta^{-1}})^{\iota}}), \end{align*} $$
where
 $\mathbb {V}^{\dagger}_{f{\boldsymbol {g}}_{\alpha }({\boldsymbol {g}}^{*}_{\beta ^{-1}})^{\iota }}\simeq (V_{p}E\otimes \text {Ind}_{K}^{\mathbf {Q}}\chi )\oplus (V_{p}E\otimes \text {Ind}_{K}^{\mathbf {Q}}\Psi _{T}^{1-\tau })$
. Thus,
$\mathbb {V}^{\dagger}_{f{\boldsymbol {g}}_{\alpha }({\boldsymbol {g}}^{*}_{\beta ^{-1}})^{\iota }}\simeq (V_{p}E\otimes \text {Ind}_{K}^{\mathbf {Q}}\chi )\oplus (V_{p}E\otimes \text {Ind}_{K}^{\mathbf {Q}}\Psi _{T}^{1-\tau })$
. Thus,
![]() ${\boldsymbol \kappa }^{\iota }$
is the restriction of (5.2) to the line of weights
${\boldsymbol \kappa }^{\iota }$
is the restriction of (5.2) to the line of weights
![]() $(\ell ,2-\ell )$
(cf.
$(\ell ,2-\ell )$
(cf.
![]() $\kappa (\breve {f},\breve {{\boldsymbol {g}}}\breve {{\boldsymbol {g}}}^{*})$
in (3.11), where the line
$\kappa (\breve {f},\breve {{\boldsymbol {g}}}\breve {{\boldsymbol {g}}}^{*})$
in (3.11), where the line
![]() $(\ell ,\ell )$
is considered). Then, by definition,
$(\ell ,\ell )$
is considered). Then, by definition,
As in Theorem 3.6, by [Reference Darmon and Rotger19, Prop. 5.8], the restriction
![]() $\text {Loc}_{p}({\boldsymbol \kappa }^{\iota })$
belongs to the natural image of
$\text {Loc}_{p}({\boldsymbol \kappa }^{\iota })$
belongs to the natural image of
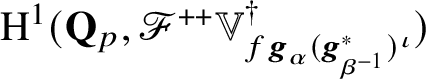 $\text {H}^{1}({\mathbf {Q}}_{p},\mathscr {F}^{++}\mathbb {V}^{\dagger}_{f{\boldsymbol {g}}_{\alpha }({\boldsymbol {g}}^{*}_{\beta ^{-1}})^{\iota }})$
in
$\text {H}^{1}({\mathbf {Q}}_{p},\mathscr {F}^{++}\mathbb {V}^{\dagger}_{f{\boldsymbol {g}}_{\alpha }({\boldsymbol {g}}^{*}_{\beta ^{-1}})^{\iota }})$
in
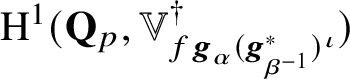 $\text {H}^{1}({\mathbf {Q}}_{p},\mathbb {V}^{\dagger}_{f{\boldsymbol {g}}_{\alpha }({\boldsymbol {g}}^{*}_{\beta ^{-1}})^{\iota }})$
, where
$\text {H}^{1}({\mathbf {Q}}_{p},\mathbb {V}^{\dagger}_{f{\boldsymbol {g}}_{\alpha }({\boldsymbol {g}}^{*}_{\beta ^{-1}})^{\iota }})$
, where
 $$ \begin{align*} \mathscr{F}^{++}\mathbb{V}_{f{\boldsymbol{g}}_{\alpha}({\boldsymbol{g}}^{*}_{\beta^{-1}})^{\iota}}^{\dagger}=V_{p}E\otimes\chi^{-1} +\mathscr{F}^{+}V_{p}E\otimes(\Psi^{1-\tau}_{T}+ \Psi^{1-\tau}_{T}). \end{align*} $$
$$ \begin{align*} \mathscr{F}^{++}\mathbb{V}_{f{\boldsymbol{g}}_{\alpha}({\boldsymbol{g}}^{*}_{\beta^{-1}})^{\iota}}^{\dagger}=V_{p}E\otimes\chi^{-1} +\mathscr{F}^{+}V_{p}E\otimes(\Psi^{1-\tau}_{T}+ \Psi^{1-\tau}_{T}). \end{align*} $$
Thus, the projection
![]() ${\boldsymbol \kappa }^{\iota }_{\infty }$
of
${\boldsymbol \kappa }^{\iota }_{\infty }$
of
![]() ${\boldsymbol \kappa }^{\iota }$
to
${\boldsymbol \kappa }^{\iota }$
to
 $\text {H}^{1}(\mathbf {Q},V_{p}E\otimes \text {Ind}_{K}^{\mathbf {Q}}\Psi _{T}^{1-\tau })\simeq \widehat {\text {H}}^{1}(K_{\infty },V_{p}E)$
is crystalline at p and therefore defines a Selmer class for
$\text {H}^{1}(\mathbf {Q},V_{p}E\otimes \text {Ind}_{K}^{\mathbf {Q}}\Psi _{T}^{1-\tau })\simeq \widehat {\text {H}}^{1}(K_{\infty },V_{p}E)$
is crystalline at p and therefore defines a Selmer class for
![]() $V_{p}E$
over the
$V_{p}E$
over the
![]() $K_{\infty }/K$
. Since under our hypotheses the space of such anticyclotomic universal norms is trivial by Cornut–Vatsal [Reference Cornut and Vatsal15], we conclude that
$K_{\infty }/K$
. Since under our hypotheses the space of such anticyclotomic universal norms is trivial by Cornut–Vatsal [Reference Cornut and Vatsal15], we conclude that
![]() ${\boldsymbol \kappa }^{\iota }_{\infty }=0$
. As in the proof of Theorem 3.6, it follows that
${\boldsymbol \kappa }^{\iota }_{\infty }=0$
. As in the proof of Theorem 3.6, it follows that
![]() $\kappa _{\alpha ,\beta ^{-1}}(f,g,g^{*})=0$
. The vanishing of
$\kappa _{\alpha ,\beta ^{-1}}(f,g,g^{*})=0$
. The vanishing of
![]() $\kappa _{\beta ,\alpha ^{-1}}(f,g,g^{*})$
is shown in the same manner.
$\kappa _{\beta ,\alpha ^{-1}}(f,g,g^{*})$
is shown in the same manner.
5.3 The leading term formula
Let
![]() $J\subseteq \Lambda $
be the augmentation ideal and let
$J\subseteq \Lambda $
be the augmentation ideal and let
Since
![]() $\Theta _{f/K}$
is nonzero by [Reference Vatsal48],
$\Theta _{f/K}$
is nonzero by [Reference Vatsal48],
![]() $\mathfrak {r}$
is a well-defined nonnegative integer. Moreover, since
$\mathfrak {r}$
is a well-defined nonnegative integer. Moreover, since
![]() $L(E/K,1)=0$
under our hypotheses,
$L(E/K,1)=0$
under our hypotheses,
![]() $\mathfrak {r}>0$
by the interpolation property. Let
$\mathfrak {r}>0$
by the interpolation property. Let
 $$ \begin{align} \textrm{Sel}(K,V_{p}E)=S_{p}^{(1)}\supseteq S_{p}^{(2)}\supseteq\cdots \supseteq S_{p}^{(i)}\supseteq \cdots \supseteq S^{(\infty)}_{p} \end{align} $$
$$ \begin{align} \textrm{Sel}(K,V_{p}E)=S_{p}^{(1)}\supseteq S_{p}^{(2)}\supseteq\cdots \supseteq S_{p}^{(i)}\supseteq \cdots \supseteq S^{(\infty)}_{p} \end{align} $$
be the filtration in Theorem 4.1, where we have put
 $S_{p}^{(i)}=S_{p}^{(i)}(E/K)$
for ease of notation, and let
$S_{p}^{(i)}=S_{p}^{(i)}(E/K)$
for ease of notation, and let
 $$ \begin{align*} h_{p}^{(i)}:S_{p}^{(i)}\times S_{p}^{(i)}\rightarrow(J^{i}/J^{i+1})\otimes_{\mathbf{Z}_{p}}{\mathbf{Q}}_{p} \end{align*} $$
$$ \begin{align*} h_{p}^{(i)}:S_{p}^{(i)}\times S_{p}^{(i)}\rightarrow(J^{i}/J^{i+1})\otimes_{\mathbf{Z}_{p}}{\mathbf{Q}}_{p} \end{align*} $$
be the associated derived p-adic height pairings. Since we assume that
![]() $N^{-}$
is the squarefree product of an odd number of primes, we have
$N^{-}$
is the squarefree product of an odd number of primes, we have
 $S_{p}^{(\infty )}=0$
by part (b) of Theorem 4.1 and the work of Cornut–Vatsal [Reference Cornut and Vatsal15].
$S_{p}^{(\infty )}=0$
by part (b) of Theorem 4.1 and the work of Cornut–Vatsal [Reference Cornut and Vatsal15].
Theorem 5.3. Let
![]() $\mathfrak {r}=\mathrm{ord}_{J}(\Theta _{f/K})$
. Then
$\mathfrak {r}=\mathrm{ord}_{J}(\Theta _{f/K})$
. Then
 $$ \begin{align} \kappa_{\alpha,\alpha^{-1}}(f,g,g^{*})\in S_{p}^{(\mathfrak{r})}, \end{align} $$
$$ \begin{align} \kappa_{\alpha,\alpha^{-1}}(f,g,g^{*})\in S_{p}^{(\mathfrak{r})}, \end{align} $$
and for every for every
 $x\in S_{p}^{(\mathfrak {r})}$
we have
$x\in S_{p}^{(\mathfrak {r})}$
we have
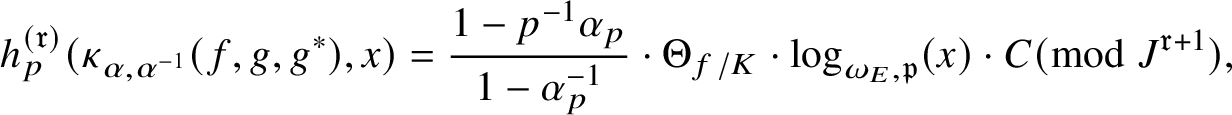 $$ \begin{align} h_{p}^{(\mathfrak{r})}(\kappa_{\alpha,\alpha^{-1}}(f,g,g^{*}),x)=\frac{1-p^{-1}\alpha_{p}}{1-\alpha_{p}^{-1}}\cdot\Theta_{f/K}\cdot\log_{\omega_{E},\mathfrak{p}}(x)\cdot C\pmod{J^{\mathfrak{r}+1}}, \end{align} $$
$$ \begin{align} h_{p}^{(\mathfrak{r})}(\kappa_{\alpha,\alpha^{-1}}(f,g,g^{*}),x)=\frac{1-p^{-1}\alpha_{p}}{1-\alpha_{p}^{-1}}\cdot\Theta_{f/K}\cdot\log_{\omega_{E},\mathfrak{p}}(x)\cdot C\pmod{J^{\mathfrak{r}+1}}, \end{align} $$
where
![]() $\alpha _{p}$
is the p-adic unit root of
$\alpha _{p}$
is the p-adic unit root of
![]() $X^{2}-a_{p}(E)X+p=0$
and C is a nonzero algebraic number with
$X^{2}-a_{p}(E)X+p=0$
and C is a nonzero algebraic number with
![]() $C^{2}\in K(\chi ,\alpha _{p})^{\times }$
.
$C^{2}\in K(\chi ,\alpha _{p})^{\times }$
.
5.4 Nonvanishing of
 $\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})$
$\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})$
Here we prove the implication (1.10) in Theorem A. Thus, suppose that
![]() $\text {dim}_{{\mathbf {Q}}_{p}}\text {Sel}(\mathbf {Q},V_{p}E)=2$
. Since
$\text {dim}_{{\mathbf {Q}}_{p}}\text {Sel}(\mathbf {Q},V_{p}E)=2$
. Since
![]() $L(E^{K},1)\neq 0$
, we have
$L(E^{K},1)\neq 0$
, we have
![]() $\text {Sel}(\mathbf {Q},V_{p}E^{K})=0$
by [Reference Kolyvagin31] (or, alternatively, [Reference Kato29]) and therefore
$\text {Sel}(\mathbf {Q},V_{p}E^{K})=0$
by [Reference Kolyvagin31] (or, alternatively, [Reference Kato29]) and therefore
where
![]() $r^{\pm }$
denotes the dimension of the
$r^{\pm }$
denotes the dimension of the
![]() $\pm $
-eigenspace of
$\pm $
-eigenspace of
![]() $\text {Sel}(K,V_{p}E)$
under the action of the complex conjugation
$\text {Sel}(K,V_{p}E)$
under the action of the complex conjugation
![]() $\tau $
. Since
$\tau $
. Since
![]() $\tau $
acts as
$\tau $
acts as
![]() $-1$
on
$-1$
on
![]() $J/J^{2}$
, part (4) of Theorem 4.1 gives
$J/J^{2}$
, part (4) of Theorem 4.1 gives
 $$ \begin{align} h_{p}^{(i)}(x^{\tau},y^{\tau})=(-1)^{r}h_{p}^{(i)}(x,y), \end{align} $$
$$ \begin{align} h_{p}^{(i)}(x^{\tau},y^{\tau})=(-1)^{r}h_{p}^{(i)}(x,y), \end{align} $$
and hence from (5.6) we see that for i odd, the null-space of
 $h_{p}^{(i)}$
(i.e.,
$h_{p}^{(i)}$
(i.e.,
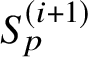 $S_{p}^{(i+1)}$
) is either 0 or 2-dimensional, with the latter case occurring as long as
$S_{p}^{(i+1)}$
) is either 0 or 2-dimensional, with the latter case occurring as long as
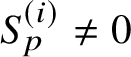 $S_{p}^{(i)}\neq 0$
. Since, on the other hand,
$S_{p}^{(i)}\neq 0$
. Since, on the other hand,
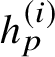 $h_{p}^{(i)}$
is a nondegenerate alternating pairing on
$h_{p}^{(i)}$
is a nondegenerate alternating pairing on
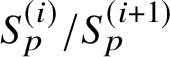 $S_{p}^{(i)}/S_{p}^{(i+1)}$
for even values of i, unless
$S_{p}^{(i)}/S_{p}^{(i+1)}$
for even values of i, unless
 $S_{p}^{(i)}=0$
, it follows that (5.3) reduces to
$S_{p}^{(i)}=0$
, it follows that (5.3) reduces to
 $$ \begin{align} \textrm{Sel}(\mathbf{Q},V_{p}E)=S_{p}^{(1)}=S_{p}^{(2)}=\cdots= S_{p}^{(r)}\supsetneq S_{p}^{(r+1)}=\cdots= S_{p}^{(\infty)}=0 \end{align} $$
$$ \begin{align} \textrm{Sel}(\mathbf{Q},V_{p}E)=S_{p}^{(1)}=S_{p}^{(2)}=\cdots= S_{p}^{(r)}\supsetneq S_{p}^{(r+1)}=\cdots= S_{p}^{(\infty)}=0 \end{align} $$
for some even
![]() $r\geqslant 2$
. By Theorem 4.1, we deduce that there is a
$r\geqslant 2$
. By Theorem 4.1, we deduce that there is a
![]() $\Lambda $
-module pseudo-isomorphism
$\Lambda $
-module pseudo-isomorphism
 $$ \begin{align*} \textrm{Sel}_{p^{\infty}}(E/K_{\infty})^{\vee}\sim(\Lambda/J^{r})^{\oplus 2}\oplus M^{\prime}, \end{align*} $$
$$ \begin{align*} \textrm{Sel}_{p^{\infty}}(E/K_{\infty})^{\vee}\sim(\Lambda/J^{r})^{\oplus 2}\oplus M^{\prime}, \end{align*} $$
where
![]() $M^{\prime }$
is a torsion
$M^{\prime }$
is a torsion
![]() $\Lambda $
-module with characteristic ideal prime-to-J. Therefore, letting
$\Lambda $
-module with characteristic ideal prime-to-J. Therefore, letting
![]() $\mathcal {L}_{p}\in \Lambda $
be any generator of the characteristic ideal of
$\mathcal {L}_{p}\in \Lambda $
be any generator of the characteristic ideal of
![]() $\text {Sel}_{p^{\infty }}(E/K_{\infty })^{\vee }$
, we have
$\text {Sel}_{p^{\infty }}(E/K_{\infty })^{\vee }$
, we have
Finally, the divisibility
 $(\Theta _{f/K}^{2})\supseteq (\mathcal {L}_{p})$
arising from [Reference Skinner and Urban45, §3.6.3] implies that
$(\Theta _{f/K}^{2})\supseteq (\mathcal {L}_{p})$
arising from [Reference Skinner and Urban45, §3.6.3] implies that
![]() $r\geqslant \mathfrak {r}$
and hence
$r\geqslant \mathfrak {r}$
and hence
 $S_{p}^{(\mathfrak {r})}=\text {Sel}(\mathbf {Q},V_{p}E)$
by (5.8). Since by our hypothesis that
$S_{p}^{(\mathfrak {r})}=\text {Sel}(\mathbf {Q},V_{p}E)$
by (5.8). Since by our hypothesis that
![]() $\text {Sel}(\mathbf {Q},V_{p}E)\neq \text {ker}(\text {Loc}_{p})$
we can find
$\text {Sel}(\mathbf {Q},V_{p}E)\neq \text {ker}(\text {Loc}_{p})$
we can find
![]() $x\in \text {Sel}(\mathbf {Q},V_{p}E)$
with
$x\in \text {Sel}(\mathbf {Q},V_{p}E)$
with
![]() $\text {log}_{\omega _{E},{\mathfrak p}}(x)\neq 0$
, the nonvanishing of
$\text {log}_{\omega _{E},{\mathfrak p}}(x)\neq 0$
, the nonvanishing of
![]() $\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})$
now follows from the leading term formula
$\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})$
now follows from the leading term formula
![]() $(5.5)$
.
$(5.5)$
.
Remark 5.4. The same argument as above with
![]() $\beta $
in place of
$\beta $
in place of
![]() $\alpha $
establishes the nonvanishing of
$\alpha $
establishes the nonvanishing of
![]() $\kappa _{\beta ,\beta ^{-1}}(f,g,g^{*})$
under the given hypotheses.
$\kappa _{\beta ,\beta ^{-1}}(f,g,g^{*})$
under the given hypotheses.
5.5 Analogue of Kolyvagin’s theorem for
 $\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})$
$\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})$
Here we prove the implication (1.9) in Theorem A. As in Subsection 5.4, we see that
![]() $\text {Sel}(K,V_{p}E)=\text {Sel}(\mathbf {Q},V_{p}E)$
and the nontrivial jumps in (5.3) can only occur at even values of i. Thus, (5.3) reduces to
$\text {Sel}(K,V_{p}E)=\text {Sel}(\mathbf {Q},V_{p}E)$
and the nontrivial jumps in (5.3) can only occur at even values of i. Thus, (5.3) reduces to
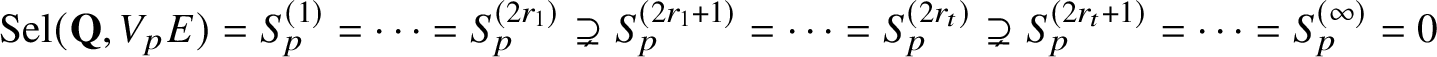 $$ \begin{align} \textrm{Sel}(\mathbf{Q},V_{p}E)=S_{p}^{(1)}=\cdots= S_{p}^{(2r_{1})}\supsetneq S_{p}^{(2r_{1}+1)}=\cdots= S_{p}^{(2r_{t})}\supsetneq S_{p}^{(2r_{t}+1)}=\cdots=S_{p}^{(\infty)}=0 \end{align} $$
$$ \begin{align} \textrm{Sel}(\mathbf{Q},V_{p}E)=S_{p}^{(1)}=\cdots= S_{p}^{(2r_{1})}\supsetneq S_{p}^{(2r_{1}+1)}=\cdots= S_{p}^{(2r_{t})}\supsetneq S_{p}^{(2r_{t}+1)}=\cdots=S_{p}^{(\infty)}=0 \end{align} $$
for some
![]() $1\leqslant r_{1}\leqslant \cdots \leqslant r_{t}$
, and by Theorem 4.1 we have
$1\leqslant r_{1}\leqslant \cdots \leqslant r_{t}$
, and by Theorem 4.1 we have
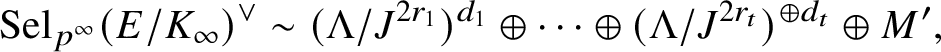 $$ \begin{align*} \textrm{Sel}_{p^{\infty}}(E/K_{\infty})^{\vee}\sim(\Lambda/J^{2r_{1}})^{d_{1}}\oplus\cdots\oplus(\Lambda/J^{2r_{t}})^{\oplus d_{t}}\oplus M^{\prime}, \end{align*} $$
$$ \begin{align*} \textrm{Sel}_{p^{\infty}}(E/K_{\infty})^{\vee}\sim(\Lambda/J^{2r_{1}})^{d_{1}}\oplus\cdots\oplus(\Lambda/J^{2r_{t}})^{\oplus d_{t}}\oplus M^{\prime}, \end{align*} $$
where
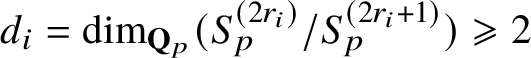 $d_{i}=\text {dim}_{{\mathbf {Q}}_{p}}(S_{p}^{(2r_{i})}/S_{p}^{(2r_{i}+1)})\geqslant 2$
and
$d_{i}=\text {dim}_{{\mathbf {Q}}_{p}}(S_{p}^{(2r_{i})}/S_{p}^{(2r_{i}+1)})\geqslant 2$
and
![]() $M^{\prime }$
is as in Subsection 5.4. Letting
$M^{\prime }$
is as in Subsection 5.4. Letting
![]() $\mathcal {L}_{p}\in \Lambda $
be a generator of the characteristic ideal of
$\mathcal {L}_{p}\in \Lambda $
be a generator of the characteristic ideal of
![]() $\text {Sel}_{p^{\infty }}(E/K_{\infty })^{\vee }$
, we therefore have
$\text {Sel}_{p^{\infty }}(E/K_{\infty })^{\vee }$
, we therefore have
Suppose now that
![]() $\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})\neq 0$
. By (5.4), it follows that
$\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})\neq 0$
. By (5.4), it follows that
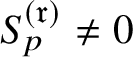 $S_{p}^{(\mathfrak {r})}\neq 0$
and therefore
$S_{p}^{(\mathfrak {r})}\neq 0$
and therefore
On the other hand, the divisibility
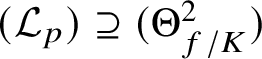 $(\mathcal {L}_{p})\supseteq (\Theta _{f/K}^{2})$
established in [Reference Bertolini and Darmon5] (as refined in [Reference Pollack and Weston38]) implies that
$(\mathcal {L}_{p})\supseteq (\Theta _{f/K}^{2})$
established in [Reference Bertolini and Darmon5] (as refined in [Reference Pollack and Weston38]) implies that
![]() $r_{1}d_{1}+\cdots + r_{t}d_{t}\leqslant \mathfrak {r}$
; together with
$r_{1}d_{1}+\cdots + r_{t}d_{t}\leqslant \mathfrak {r}$
; together with
![]() $(5.11)$
this yields
$(5.11)$
this yields
from which we conclude that
![]() $t=1$
,
$t=1$
,
![]() $d_{1}=2$
and
$d_{1}=2$
and
![]() $\text {dim}_{{\mathbf {Q}}_{p}}\text {Sel}(\mathbf {Q},V_{p}E)=2$
.
$\text {dim}_{{\mathbf {Q}}_{p}}\text {Sel}(\mathbf {Q},V_{p}E)=2$
.
5.6 Proof of Theorem B
This will follow from essentially the same argument as in Subsection 5.4 but without the need to appeal to [Reference Skinner and Urban45].
Let the hypotheses be as in the statement of Theorem B and assume that
![]() $\text {ord}_{T}(\Theta _{f/K})=2$
. Then Theorem 5.3 gives the inclusion
$\text {ord}_{T}(\Theta _{f/K})=2$
. Then Theorem 5.3 gives the inclusion
 $$ \begin{align*} \kappa_{\alpha,\alpha^{-1}}(f,g,g^{*})\in S_{p}^{(2)}. \end{align*} $$
$$ \begin{align*} \kappa_{\alpha,\alpha^{-1}}(f,g,g^{*})\in S_{p}^{(2)}. \end{align*} $$
As in Subsection 5.4, the assumption that
![]() $L(E^{K},1)\neq 0$
implies that
$L(E^{K},1)\neq 0$
implies that
![]() $\text {Sel}(K,V_{p}E)=\text {Sel}(\mathbf {Q},V_{p}E)$
. Since by (5.7) the
$\text {Sel}(K,V_{p}E)=\text {Sel}(\mathbf {Q},V_{p}E)$
. Since by (5.7) the
![]() $\tau $
-eigenspaces of
$\tau $
-eigenspaces of
![]() $\text {Sel}(K,V_{p}E)$
are isotropic under
$\text {Sel}(K,V_{p}E)$
are isotropic under
 $h_{p}^{(1)}$
, we see that
$h_{p}^{(1)}$
, we see that
 $$ \begin{align*} S_{p}^{(2)}=\textrm{Sel}(K,V_{p}E)=\textrm{Sel}(\mathbf{Q},V_{p}E). \end{align*} $$
$$ \begin{align*} S_{p}^{(2)}=\textrm{Sel}(K,V_{p}E)=\textrm{Sel}(\mathbf{Q},V_{p}E). \end{align*} $$
Finally, since our assumption that
![]() $E(\mathbf {Q})$
has positive rank implies that
$E(\mathbf {Q})$
has positive rank implies that
![]() $\text {Sel}(\mathbf {Q},V_{p}E)\neq \text {ker}(\text {Loc}_{p})$
(see Remark 1.5), the nonvanishing of
$\text {Sel}(\mathbf {Q},V_{p}E)\neq \text {ker}(\text {Loc}_{p})$
(see Remark 1.5), the nonvanishing of
![]() $\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})$
follows from the leading term formula of Theorem 5.3. The same argument yields the nonvanishing of
$\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})$
follows from the leading term formula of Theorem 5.3. The same argument yields the nonvanishing of
![]() $\kappa _{\beta ,\beta ^{-1}}(f,g,g^{*})$
.
$\kappa _{\beta ,\beta ^{-1}}(f,g,g^{*})$
.
5.7 Application to the strong elliptic Stark conjecture
We keep the setting from the beginning of this section but assume in addition that
![]() .
.
As explained in [Reference Darmon and Rotger17, §4.5.3], the p-adic regulators appearing in the elliptic Stark conjectures of [Reference Darmon, Lauder and Rotger16] all vanish in the setting we have placed ourselves in. As a remedy, in [Reference Darmon and Rotger17] they formulated a strengthening of those conjectures in terms of certain enhanced regulators; in our setting, they are given (modulo
![]() $\mathbf {Q}^{\times }$
) by
$\mathbf {Q}^{\times }$
) by
where
![]() $(P,Q)$
is any basis of
$(P,Q)$
is any basis of
![]() $E(\mathbf {Q})\otimes _{\mathbf {Z}}\mathbf {Q}$
. The strong elliptic Stark conjecture then predicts that the generalised Kato classes
$E(\mathbf {Q})\otimes _{\mathbf {Z}}\mathbf {Q}$
. The strong elliptic Stark conjecture then predicts that the generalised Kato classes
![]() $\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})$
and
$\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})$
and
![]() $\kappa _{\beta ,\beta ^{-1}}(f,g,g^{*})$
both agree with
$\kappa _{\beta ,\beta ^{-1}}(f,g,g^{*})$
both agree with
![]() $\text {Log}_{p}(P\wedge Q)$
up to a nonzero algebraic constant.
$\text {Log}_{p}(P\wedge Q)$
up to a nonzero algebraic constant.
In the direction of this conjecture, our methods show that
![]() $\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})$
and
$\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})$
and
![]() $\kappa _{\beta ,\beta ^{-1}}(f,g,g^{*})$
span the same p-adic line as
$\kappa _{\beta ,\beta ^{-1}}(f,g,g^{*})$
span the same p-adic line as
![]() $\text {Log}_{p}(P\wedge Q)$
inside the
$\text {Log}_{p}(P\wedge Q)$
inside the
![]() $2$
-dimensional
$2$
-dimensional
![]() $\text {Sel}(\mathbf {Q},V_{p}E)$
.
$\text {Sel}(\mathbf {Q},V_{p}E)$
.
To state the application, we identify
![]() $J^{\mathfrak {r}}/J^{\mathfrak {r}+1}$
with
$J^{\mathfrak {r}}/J^{\mathfrak {r}+1}$
with
![]() $\mathbf {Z}_{p}$
in the usual manner by choosing a topological generator of
$\mathbf {Z}_{p}$
in the usual manner by choosing a topological generator of
![]() $\Gamma _{\infty }$
and let
$\Gamma _{\infty }$
and let
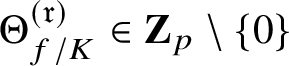 $\Theta _{f/K}^{(\mathfrak {r})}\in \mathbf {Z}_{p}\smallsetminus \{0\}$
denote the image of
$\Theta _{f/K}^{(\mathfrak {r})}\in \mathbf {Z}_{p}\smallsetminus \{0\}$
denote the image of
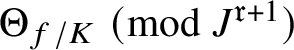 $\Theta _{f/K}\;(\text {mod}\;J^{\mathfrak {r}+1})$
under this identification.
$\Theta _{f/K}\;(\text {mod}\;J^{\mathfrak {r}+1})$
under this identification.
Theorem 5.5. Let the setting be as in the beginning of Section 5 and let
![]() $\mathfrak {r}=\mathrm{ord}_{J}(\Theta _{f/K})$
. Then, as elements of
$\mathfrak {r}=\mathrm{ord}_{J}(\Theta _{f/K})$
. Then, as elements of
![]() $\mathrm{Sel}(\mathbf {Q},V_{p}E)\simeq E(\mathbf {Q})\otimes _{\mathbf {Z}}{\mathbf {Q}}_{p}$
, we have
$\mathrm{Sel}(\mathbf {Q},V_{p}E)\simeq E(\mathbf {Q})\otimes _{\mathbf {Z}}{\mathbf {Q}}_{p}$
, we have
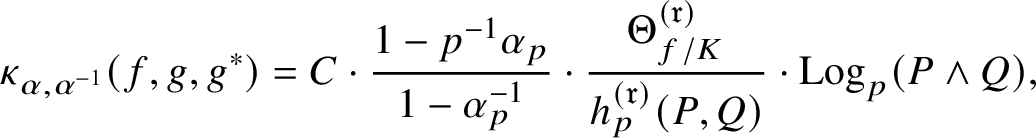 $$ \begin{align*} \kappa_{\alpha,\alpha^{-1}}(f,g,g^{*})=C\cdot \frac{1-p^{-1}\alpha_{p}}{1-\alpha_{p}^{-1}}\cdot\frac{\Theta_{f/K}^{(\mathfrak{r})}}{h_{p}^{(\mathfrak{r})}(P,Q)}\cdot\mathrm{Log}_{p}(P\wedge Q), \end{align*} $$
$$ \begin{align*} \kappa_{\alpha,\alpha^{-1}}(f,g,g^{*})=C\cdot \frac{1-p^{-1}\alpha_{p}}{1-\alpha_{p}^{-1}}\cdot\frac{\Theta_{f/K}^{(\mathfrak{r})}}{h_{p}^{(\mathfrak{r})}(P,Q)}\cdot\mathrm{Log}_{p}(P\wedge Q), \end{align*} $$
where C is nonzero and such that
![]() $C^{2}\in K(\chi ,\alpha _{p})^{\times }$
. The same result holds of
$C^{2}\in K(\chi ,\alpha _{p})^{\times }$
. The same result holds of
![]() $\kappa _{\beta ,\beta ^{-1}}(f,g,g^{*})$
.
$\kappa _{\beta ,\beta ^{-1}}(f,g,g^{*})$
.
Proof. Immediate from the leading term formula of Subsection 5.3 applied to
![]() $x=P$
and Q.
$x=P$
and Q.
Remark 5.6. The term
 $h_{p}^{(\mathfrak {r})}(P,Q)$
recovers the derived p-adic regulator
$h_{p}^{(\mathfrak {r})}(P,Q)$
recovers the derived p-adic regulator
![]() $R_{der}$
introduced in [Reference Bertolini and Darmon3]. Thus, Theorem 5.5 links the conjectural algebraicity of the ratio between
$R_{der}$
introduced in [Reference Bertolini and Darmon3]. Thus, Theorem 5.5 links the conjectural algebraicity of the ratio between
![]() $\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})$
and
$\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})$
and
![]() $\text {Log}_{p}(P\wedge Q)$
, as predicted in [Reference Darmon and Rotger17, §4.5.3], to a refinement of the p-adic Birch and Swinnerton-Dyer conjecture in [Reference Bertolini and Darmon4, Conjecture 4.3] formulated in terms of
$\text {Log}_{p}(P\wedge Q)$
, as predicted in [Reference Darmon and Rotger17, §4.5.3], to a refinement of the p-adic Birch and Swinnerton-Dyer conjecture in [Reference Bertolini and Darmon4, Conjecture 4.3] formulated in terms of
![]() $R_{der}$
.
$R_{der}$
.
6 Appendix. Nonvanishing of
 $\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})$
: Numerical examples
$\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})$
: Numerical examples
In this appendix, we exhibit the first examples of elliptic curves E over
![]() $\mathbf {Q}$
of rank 2 with nonvanishing generalised Kato classes by numerically verifying the conditions in Theorem B.
$\mathbf {Q}$
of rank 2 with nonvanishing generalised Kato classes by numerically verifying the conditions in Theorem B.
Setting
In the examples tabulated below, we take elliptic curves
![]() $E/\mathbf {Q}$
with
$E/\mathbf {Q}$
with
of conductor
![]() $N\in \{q,2q\}$
, with q an odd prime and pairs
$N\in \{q,2q\}$
, with q an odd prime and pairs
![]() $(p,-d)$
consisting of a prime
$(p,-d)$
consisting of a prime
![]() $p>3$
and a squarefree integer
$p>3$
and a squarefree integer
![]() $-d<0$
such that
$-d<0$
such that
-
•
 $K=\mathbf {Q}(\sqrt {-d})$
has class number 1, q is inert in K and
$K=\mathbf {Q}(\sqrt {-d})$
has class number 1, q is inert in K and
 $L(E^{K},1)\neq 0$
,
$L(E^{K},1)\neq 0$
, -
• p splits in K and
 $E[p]$
is irreducible as a
$E[p]$
is irreducible as a
 $G_{\mathbf {Q}}$
-module.
$G_{\mathbf {Q}}$
-module.
Note that such pairs
![]() $(p,-d)$
can be easily produced. Indeed, [Reference Ribet39, Thm. 1.1] implies that
$(p,-d)$
can be easily produced. Indeed, [Reference Ribet39, Thm. 1.1] implies that
![]() $E[p]$
must ramify at
$E[p]$
must ramify at
![]() $N^{-}=q$
, and the irreducibility of
$N^{-}=q$
, and the irreducibility of
![]() $E[p]$
can be verified either by [Reference Mazur33] when
$E[p]$
can be verified either by [Reference Mazur33] when
![]() $p\geqslant 11$
or by checking (from, e.g., Cremona’s tables) that E does not admit any rational m-isogenies for
$p\geqslant 11$
or by checking (from, e.g., Cremona’s tables) that E does not admit any rational m-isogenies for
![]() $m>3$
.
$m>3$
.
For every such triple
![]() $(E,p,-d)$
, there is a ring class character
$(E,p,-d)$
, there is a ring class character
![]() $\chi $
of K of
$\chi $
of K of
![]() $\ell $
-power conductor for some prime
$\ell $
-power conductor for some prime
![]() $\ell \nmid Np$
such that
$\ell \nmid Np$
such that
![]() $L(E/K,\chi ,1)\neq 0$
. (In fact, there are infinitely many such
$L(E/K,\chi ,1)\neq 0$
. (In fact, there are infinitely many such
![]() $\chi $
, as follows from [Reference Vatsal48, Thm. 1.3] and its extension in [Reference Chida and Hsieh13, Thm. D].) Writing
$\chi $
, as follows from [Reference Vatsal48, Thm. 1.3] and its extension in [Reference Chida and Hsieh13, Thm. D].) Writing
![]() $\chi =\psi /\psi ^{\tau }$
and letting
$\chi =\psi /\psi ^{\tau }$
and letting
![]() $g=\theta _{\psi }$
and
$g=\theta _{\psi }$
and
![]() $g^{*}=\theta _{\psi ^{-1}}$
, we then have the class
$g^{*}=\theta _{\psi ^{-1}}$
, we then have the class
as in Subsection 5.2 (see Lemma 5.1). By Theorem B, to verify the nonvanishing of
![]() $\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})$
, it suffices to check that
$\kappa _{\alpha ,\alpha ^{-1}}(f,g,g^{*})$
, it suffices to check that
Verifying order of vanishing
 $2$
$2$
Let B be the definite quaternion algebra over
![]() $\mathbf {Q}$
of discriminant q, let
$\mathbf {Q}$
of discriminant q, let
![]() $R\subset B$
be an Eichler order of level
$R\subset B$
be an Eichler order of level
![]() $N/q$
and let
$N/q$
and let
![]() $\text {Cl}(R)$
be the class group of R. Let
$\text {Cl}(R)$
be the class group of R. Let
be the Hecke eigenfunction associated to f by Jacquet–Langlands, normalised so that
![]() $\phi _{f}\not \equiv 0\pmod {p}$
. Fix an isomorphism
$\phi _{f}\not \equiv 0\pmod {p}$
. Fix an isomorphism
![]() $i_{p}:R\otimes \mathbf {Z}_{p}\simeq \text {M}_{2}(\mathbf {Z}_{p})$
and an optimal embedding
$i_{p}:R\otimes \mathbf {Z}_{p}\simeq \text {M}_{2}(\mathbf {Z}_{p})$
and an optimal embedding
![]() $\mathcal O_{K}\hookrightarrow R$
such that K is sent to a subspace consisting of diagonal matrices, and for
$\mathcal O_{K}\hookrightarrow R$
such that K is sent to a subspace consisting of diagonal matrices, and for
![]() $a\in \mathbf {Z}_{p}^{\times }$
and
$a\in \mathbf {Z}_{p}^{\times }$
and
![]() $n\geqslant 0$
put
$n\geqslant 0$
put
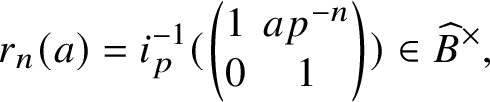 $$ \begin{align*} r_{n}(a)=i_{p}^{-1}(\begin{pmatrix} 1&ap^{-n}\\ 0&1\end{pmatrix})\in \widehat B^{\times}, \end{align*} $$
$$ \begin{align*} r_{n}(a)=i_{p}^{-1}(\begin{pmatrix} 1&ap^{-n}\\ 0&1\end{pmatrix})\in \widehat B^{\times}, \end{align*} $$
where
![]() $\widehat B=B\otimes _{\mathbf {Z}}\widehat {\mathbf {Z}}$
is the adelic completion of B.
$\widehat B=B\otimes _{\mathbf {Z}}\widehat {\mathbf {Z}}$
is the adelic completion of B.
Consider the sequence
![]() $\{P^{a}_{n}\}_{n\geqslant 0}$
of right R-ideals given by
$\{P^{a}_{n}\}_{n\geqslant 0}$
of right R-ideals given by
 $P_{n}^{a}:=(r_{n}(a)\widehat R)\cap B$
and define the nth theta element
$P_{n}^{a}:=(r_{n}(a)\widehat R)\cap B$
and define the nth theta element
![]() $\Theta _{f/K,n}\in \mathbf {Z}_{p}[T]$
by
$\Theta _{f/K,n}\in \mathbf {Z}_{p}[T]$
by
 $$ \begin{align*} \Theta_{f/K,n}:=\frac{1}{\alpha_{p}^{n+1}}\sum_{i=0}^{p^{n}-1}\sum_{a\in \mu_{p-1}}\left(\alpha_{p}\cdot\phi_{f}(P_{n}^{a{\mathbf u}^{i}})-\phi_{f}(P_{n+1}^{a{\mathbf u}^{i}})\right)(1+T)^{i},\end{align*} $$
$$ \begin{align*} \Theta_{f/K,n}:=\frac{1}{\alpha_{p}^{n+1}}\sum_{i=0}^{p^{n}-1}\sum_{a\in \mu_{p-1}}\left(\alpha_{p}\cdot\phi_{f}(P_{n}^{a{\mathbf u}^{i}})-\phi_{f}(P_{n+1}^{a{\mathbf u}^{i}})\right)(1+T)^{i},\end{align*} $$
where
![]() $\alpha _{p}$
is the p-adic unit root of
$\alpha _{p}$
is the p-adic unit root of
![]() $x^{2}-a_{p}(E)x+p$
and
$x^{2}-a_{p}(E)x+p$
and
![]() ${\mathbf u}=1+p$
.
${\mathbf u}=1+p$
.
By the definition of
![]() $\Theta _{f/K}$
(see, e.g., [Reference Bertolini and Darmon4, §2.7]), we have
$\Theta _{f/K}$
(see, e.g., [Reference Bertolini and Darmon4, §2.7]), we have
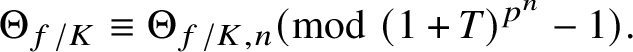 $$ \begin{align*} \Theta_{f/K}&\equiv\Theta_{f/K,n}\pmod{(1+T)^{p^{n}}-1}. \end{align*} $$
$$ \begin{align*} \Theta_{f/K}&\equiv\Theta_{f/K,n}\pmod{(1+T)^{p^{n}}-1}. \end{align*} $$
Since
![]() $(p^{n},(1+T)^{p^{n}}-1)\subset (p^{n},T^{p})$
, in the examples listed in the following Tables 1 and 2 we could verify (6.1) by computing
$(p^{n},(1+T)^{p^{n}}-1)\subset (p^{n},T^{p})$
, in the examples listed in the following Tables 1 and 2 we could verify (6.1) by computing
![]() $\Theta _{f/K,n}\;\text {mod}\;(p^{n},T^{p})$
for
$\Theta _{f/K,n}\;\text {mod}\;(p^{n},T^{p})$
for
![]() $n=2$
and
$n=2$
and
![]() $3$
, respectively. The computations were done using the Brandt module package in SAGE.
$3$
, respectively. The computations were done using the Brandt module package in SAGE.
Table 1 Examples with
![]() $\mathrm{ord}_{T}(\Theta _{f/K})=2$
determined mod
$\mathrm{ord}_{T}(\Theta _{f/K})=2$
determined mod
![]() $(p^{2},T^{p})$
.
$(p^{2},T^{p})$
.

Table 2 Examples with
![]() $\mathrm{ord}_{T}(\Theta _{f/K})=2$
determined mod
$\mathrm{ord}_{T}(\Theta _{f/K})=2$
determined mod
![]() $(p^{3},T^{p})$
.
$(p^{3},T^{p})$
.
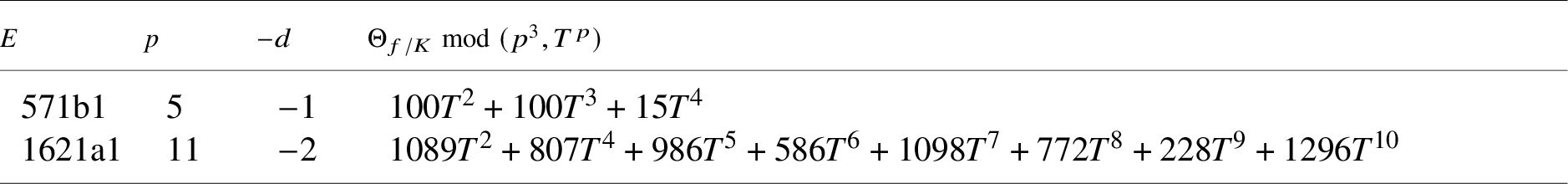
Acknowledgments
It is a pleasure to thank John Coates, Henri Darmon, Dick Gross, Barry Mazur and Victor Rotger for their comments on an earlier draft of this article. We also thank the anonymous referees for useful suggestions that helped us improve the exposition of our results. F. C. was partially supported by the NSF grants DMS-1801385, 1946136 and DMS-2101458. M.-L. H. was partially supported by the MOST grant 108-2628-M-001-009-MY4.
Conflict of interest
None.